Evaluation of Three Parametric Models for Estimating Directional Thermal Radiation from Simulation, Airborne, and Satellite Data
Abstract
:1. Introduction
2. Data
2.1. Simulation Dataset
2.2. Airborne Dataset
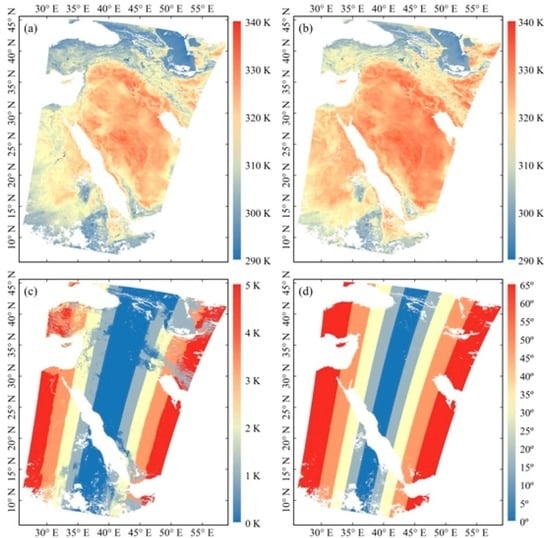
2.3. Satellite Dataset
- (1)
- The pixel’s LST should not exceed a certain variability in a 5 × 5 moving window and the standard deviation (STD) should be less than 1 K [33];
- (2)
- If more than 23 pixels have the same land cover type as the centered pixel inside the 5 × 5 window, the centered pixel is considered to be in a ‘‘pure homogenous or quasi-homogenous area’’ and should be retained [34].
2.4. SURFRAD Dataset
3. Parametric Models
3.1. RL Model
3.2. BRDF Model
3.3. Vinnikov Model
4. Evaluations and Results
4.1. Evaluation Using Simulations
4.2. Evaluation Using Airborne Data
4.3. Evaluation Using Satellite Data
5. Application
6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tang, B.-H.; Bi, Y.; Li, Z.-L.; Xia, J. Generalized split-window algorithm for estimate of land surface temperature from Chinese geostationary FengYun meteorological satellite (FY-2C) data. Sensors 2008, 8, 933–951. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Zhang, R.; Sun, X.; Li, Z.-L.; Stoll, M.P.; SU, H.; Tang, X. Revealing of major factors in the directional thermal radiation of ground objects: A new way for improving the precision of directional radiant temperature measuring and data analysis. Sci. China Ser. E 2000, 43, 34. [Google Scholar] [CrossRef]
- Vinnikov, K.Y.; Yu, Y.; Goldberg, M.D.; Tarpley, D.; Romanov, P.; Laszlo, I.; Chen, M. Angular anisotropy of satellite observations of land surface temperature. Geophys. Res. Lett. 2012, 39, L23802. [Google Scholar] [CrossRef]
- Smith, J.A.; Goltz, S. A thermal exitance and energy balance model for forest canopies. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1060–1066. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Kerr, Y.; Brunet, Y. An experimental study of angular effects on surface temperature for various plant canopies and bare soils. Agric. For. Meteorol. 1995, 77, 167–190. [Google Scholar] [CrossRef]
- Li, Z.-L.; Zhang, R.; Sun, X.; Su, H.; Tang, X.; Zhu, Z.; Sobrino, J. Experimental system for the study of the directional thermal emission of natural surfaces. Int. J. Remote Sens. 2004, 25, 195–204. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Irvine, M. Directional anisotropy in thermal infrared measurements over Toulouse city centre during the CAPITOUL measurement campaigns: first results. Meteorol. Atmos. Phys. 2008, 102, 173–185. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Hénon, A.; Kurz, B.; Moreau, P.; Irvine, M.; Voogt, J.; Mestayer, P. Modelling daytime thermal infrared directional anisotropy over Toulouse city centre. Remote Sens. Environ. 2010, 114, 87–105. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Dayau, S.; Moreau, P.; Guyon, D. Directional anisotropy of brightness surface temperature over vineyards: Case study over the Medoc region (SW France). IEEE Geosci. Remote Sens. Lett. 2014, 11, 574–578. [Google Scholar] [CrossRef]
- Sun, H. Experimental Study of Field Measurement Method of Thermal Infrared Directionality Over Forest Canopy Using Crane Platform; Beijing Forestry University: Beijing, China, 2016. [Google Scholar]
- Guillevic, P.C.; Gastellu-Etchegorry, J.; Demarty, J.; Prévot, L. Thermal infrared radiative transfer within three-dimensional vegetation covers. J. Geophys. Res. Atmos. 2003, 108, 4248. [Google Scholar] [CrossRef]
- Guillevic, P.C.; Bork-Unkelbach, A.; Göttsche, F.M.; Hulley, G.; Gastellu-Etchegorry, J.-P.; Olesen, F.S.; Privette, J.L. Directional viewing effects on satellite land surface temperature products over sparse vegetation canopies—A multisensor analysis. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1464–1468. [Google Scholar] [CrossRef]
- Verhoef, W.; Jia, L.; Xiao, Q.; Su, Z. Unified optical-thermal four-stream radiative transfer theory for homogeneous vegetation canopies. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1808–1822. [Google Scholar] [CrossRef]
- Duffour, C.; Olioso, A.; Demarty, J.; Van der Tol, C.; Lagouarde, J.-P. An evaluation of SCOPE: A tool to simulate the directional anisotropy of satellite-measured surface temperatures. Remote Sens. Environ. 2015, 158, 362–375. [Google Scholar] [CrossRef]
- Duffour, C.; Lagouarde, J.-P.; Olioso, A.; Demarty, J.; Roujean, J.-L. Driving factors of the directional variability of thermal infrared signal in temperate regions. Remote Sens. Environ. 2016, 177, 248–264. [Google Scholar] [CrossRef]
- Duffour, C.; Lagouarde, J.-P.; Roujean, J.-L. A two parameter model to simulate thermal infrared directional effects for remote sensing applications. Remote Sens. Environ. 2016, 186, 250–261. [Google Scholar] [CrossRef]
- Peng, J.; Liu, Q.; Liu, Q.; Li, J.; Ma, H.; Li, F. Kernel-driven model fitting of multi-angle thermal infrared brightness temperature and its applicaion. J. Infrared Millim. Waves 2011, 30, 361–365. [Google Scholar] [CrossRef]
- Ren, H.; Yan, G.; Liu, R.; Li, Z.-L.; Qin, Q.; Nerry, F.; Liu, Q. Determination of optimum viewing angles for the angular normalization of land surface temperature over vegetated surface. Sensors 2015, 15, 7537–7570. [Google Scholar] [CrossRef] [PubMed]
- Ermida, S.L.; DaCamara, C.C.; Trigo, I.F.; Pires, A.C.; Ghent, D.; Remedios, J. Modelling directional effects on remotely sensed land surface temperature. Remote Sens. Environ. 2017, 190, 56–69. [Google Scholar] [CrossRef]
- Liu, Q.; Yan, C.; Xiao, Q.; Yan, G.; Fang, L. Separating vegetation and soil temperature using airborne multiangular remote sensing image data. Int. J. Appl. Earth Obser. Geoinform. 2012, 17, 66–75. [Google Scholar] [CrossRef]
- Minnis, P.; Khaiyer, M.M. Anisotropy of land surface skin temperature derived from satellite data. J. Appl. Meteorol. 2000, 39, 1117–1129. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+ SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Li, Z.; Ma, M.; Wang, J.; Xiao, Q.; Liu, Q.; Che, T.; Chen, E.; Yan, G. Watershed allied telemetry experimental research. J. Geophys. Res. Atmos. 2009, 114, D22103. [Google Scholar] [CrossRef]
- Bo, Y.; Liu, Z.; Fu, Z.; Li, B.; Lin, H.; Song, D.; Sun, Z.; Gong, H.; Zhu, M. WATER: Dataset of land use and land cover investigation in the arid region hydrology and forest hydrology experiment areas. Heihe Plan Sci. Data Center 2010. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Snyder, W.C.; Wan, Z.; Zhang, Y.; Feng, Y.-Z. Classification-based emissivity for land surface temperature measurement from space. Int. J. Remote Sens. 1998, 19, 2753–2774. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z.-L. Radiance-based validation of the V5 MODIS land-surface temperature product. Int. J. Remote Sens. 2008, 29, 5373–5395. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Prata, A. Land surface temperature measurement from space: AATSR algorithm theoretical basis document. Contract Rep. ESA CSIRO Atmos. Res. Aspendale Vic. Aust. 2002, 2002, 1–34. [Google Scholar]
- Ghent, D. Land Surface Temperature Validation and Algorithm Verification; Report to European Space Agency; European Space Agency: Paris, France, 2012. [Google Scholar]
- Wan, Z. Collection-6 MODIS Land Surface Temperature Products Users’ Guide; ICESS; University of California: Santa Barbara, CA, USA, 2013; pp. 1–33. [Google Scholar]
- Frey, C.M.; Kuenzer, C.; Dech, S. Quantitative comparison of the operational NOAA-AVHRR LST product of DLR and the MODIS LST product V005. Int. J. Remote Sens. 2012, 33, 7165–7183. [Google Scholar] [CrossRef]
- Ren, H.; Yan, G.; Chen, L.; Li, Z. Angular effect of MODIS emissivity products and its application to the split-window algorithm. ISPRS J. Photogramm. Remote Sens. 2011, 66, 498–507. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L. Intercomparison of operational land surface temperature products derived from MSG-SEVIRI and Terra/Aqua-MODIS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4163–4170. [Google Scholar] [CrossRef]
- Tang, B.-H.; Wu, H.; Li, C.; Li, Z.-L. Estimation of broadband surface emissivity from narrowband emissivities. Opt. Exp. 2011, 19, 185–192. [Google Scholar] [CrossRef] [PubMed]
- Roujean, J.-L. A parametric hot spot model for optical remote sensing applications. Remote Sens. Environ. 2000, 71, 197–206. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Geometric-optical bidirectional reflectance modeling of the discrete crown vegetation canopy: Effect of crown shape and mutual shadowing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 276–292. [Google Scholar] [CrossRef]
- Hu, T.; Du, Y.; Cao, B.; Li, H.; Bian, Z.; Sun, D.; Liu, Q. Estimation of upward longwave radiation from vegetated surfaces considering thermal directionality. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6644–6658. [Google Scholar] [CrossRef]
- Hu, T.; Cao, B.; Du, Y.; Li, H.; Wang, C.; Bian, Z.; Sun, D.; Liu, Q. Estimation of Surface Upward Longwave Radiation Using a Direct Physical Algorithm. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4412–4426. [Google Scholar] [CrossRef]
- Pinheiro, A.C.; Privette, J.L.; Guillevic, P. Modeling the observed angular anisotropy of land surface temperature in a savanna. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1036–1047. [Google Scholar] [CrossRef]
- Ren, H.; Liu, R.; Yan, G.; Li, Z.-L.; Qin, Q.; Liu, Q.; Nerry, F. Performance evaluation of four directional emissivity analytical models with thermal SAIL model and airborne images. Opt. Exp. 2015, 23, A346–A360. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Liu, R.; Yan, G.; Mu, X.; Li, Z.-L.; Nerry, F.; Liu, Q. Angular normalization of land surface temperature and emissivity using multiangular middle and thermal infrared data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4913–4931. [Google Scholar]
- Bian, Z.; Xiao, Q.; Cao, B.; Du, Y.; Li, H.; Wang, H.; Liu, Q.; Liu, Q. Retrieval of leaf, sunlit soil, and shaded soil component temperatures using airborne thermal infrared multiangle observations. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4660–4671. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Sòria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Plaza, A.; Martínez, P. Land surface emissivity retrieval from different VNIR and TIR sensors. IEEE Trans. Geosci. Remote Sens. 2008, 46, 316–327. [Google Scholar] [CrossRef]









| No. | Long. (°E) | Lat (°N) | Land Cover | LAI | Area (m × m) | UTC (hh:mm:ss) | Number of Images | Mean Tdiff (K) |
|---|---|---|---|---|---|---|---|---|
| 1 | 100.264 | 38.559 | Settlement | \ | 375 × 280 | 04:13:14–04:13:42 | 8 | 7.7 |
| 2 | 100.245 | 38.515 | Wheat | 3.4 | 340 × 315 | 03:58:10–03:58:38 | 8 | 1.7 |
| 3 | 100.247 | 38.512 | Maize | 4.2 | 310 × 260 | 03:58:10–03:58:34 | 7 | 1.4 |
| 4 | 100.239 | 38.509 | Orchard | 2.4 | 330 × 320 | 03:58:26–03:58:54 | 8 | 3.9 |
| 5 | 100.232 | 38.494 | Sea buckthorn | 1.9 | 315 × 245 | 03:59:14–03:59:42 | 8 | 2.9 |
| 6 | 100.193 | 38.459 | Bare soil | \ | 530 × 375 | 04:26:58–04:27:18 | 6 | 1.8 |
| Station Name | Land Cover | Long. (°W) | Lat (°N) | Number of Observations |
|---|---|---|---|---|
| Bondville, IL | Cropland | 88.373 | 40.051 | 52 |
| Boulder, CO | Bare soil | 105.238 | 40.126 | 35 |
| Fort Peck, MT | Grassland | 105.102 | 48.308 | 47 |
| Goodwin Creek, MS | Grassland | 89.873 | 34.255 | 171 |
| Penn State, PA | Cropland | 77.931 | 40.720 | 23 |
| Sioux Falls, SD | Grassland | 96.623 | 43.734 | 68 |
| Land Cover Class | A | D | Number of Points | RMSE (K) | Land Cover Class | A | D | Number of Points | RMSE (K) |
|---|---|---|---|---|---|---|---|---|---|
| 0 | −0.0067 | −0.0015 | 18,073 | 0.85 | 8 | −0.0178 | 0.0044 | 33,697 | 1.14 |
| 1 | −0.0068 | −0.0002 | 3284 | 0.72 | 9 | −0.0175 | 0.0045 | 59,706 | 1.35 |
| 2 | −0.0173 | 0.0046 | 47,542 | 0.91 | 10 | −0.0228 | 0.0005 | 78,303 | 1.62 |
| 3 | −0.0102 | 0.0034 | 15,485 | 0.79 | 11 | −0.0115 | 0.0024 | 22,325 | 0.87 |
| 4 | −0.0214 | −0.0023 | 5602 | 0.98 | 12 | −0.0184 | 0.0022 | 40,985 | 1.44 |
| 5 | −0.0093 | 0.0016 | 34,211 | 0.86 | 14 | −0.0279 | 0.0041 | 32,568 | 1.57 |
| 7 | −0.0045 | −0.0078 | 5612 | 0.84 | 16 | −0.0209 | −0.0005 | 250,395 | 1.42 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Tang, B.-H.; Li, Z.-L. Evaluation of Three Parametric Models for Estimating Directional Thermal Radiation from Simulation, Airborne, and Satellite Data. Remote Sens. 2018, 10, 420. https://doi.org/10.3390/rs10030420
Liu X, Tang B-H, Li Z-L. Evaluation of Three Parametric Models for Estimating Directional Thermal Radiation from Simulation, Airborne, and Satellite Data. Remote Sensing. 2018; 10(3):420. https://doi.org/10.3390/rs10030420
Chicago/Turabian StyleLiu, Xiangyang, Bo-Hui Tang, and Zhao-Liang Li. 2018. "Evaluation of Three Parametric Models for Estimating Directional Thermal Radiation from Simulation, Airborne, and Satellite Data" Remote Sensing 10, no. 3: 420. https://doi.org/10.3390/rs10030420
APA StyleLiu, X., Tang, B. -H., & Li, Z. -L. (2018). Evaluation of Three Parametric Models for Estimating Directional Thermal Radiation from Simulation, Airborne, and Satellite Data. Remote Sensing, 10(3), 420. https://doi.org/10.3390/rs10030420