IMF-Slices for GPR Data Processing Using Variational Mode Decomposition Method
Abstract
:1. Introduction
2. Methods
2.1. The Variational Mode Decomposition
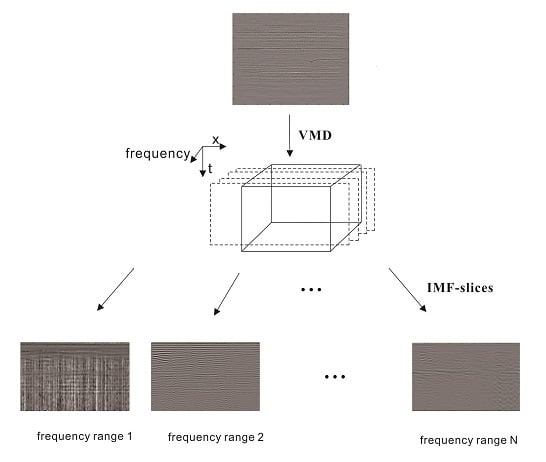
2.2. IMF-Slices of GPR Data
3. Results
3.1. Synthetic Benchmark Tests
3.2. Laboratory Data Tests
4. The Use of VMD with Field Dataset
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| GPR | ground-penetrating radar |
| EMD | empirical mean decomposition |
| IMF | intrinsic mode function |
| VMD | variational mode decomposition |
| ADMM | alternate direction method of multipliers |
References
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Seri. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Rioul, O.; Vetterli, M. Wavelets and signal processing. IEEE Signal Process. Mag. 1991, 8, 14–38. [Google Scholar] [CrossRef]
- Sinha, S.; Routh, P.; Anno, P.; Castagna, J. Spectral Decomposition of Seismic Data with Continuous Wavelet Transform. Geophysics 2005, 70, P19–P25. [Google Scholar] [CrossRef]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Cheng, Z.; Chen, W.; Chen, Y.; Liu, Y.; Liu, W.; Li, H.; Yang, R. Application of bi-Gaussian S-transform in high-resolution seismic time-frequency analysis. Interpretation 2017, 5, SC1–SC7. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, X.; Liu, C.; Lu, Q. Single-channel and multi-channel orthogonal matching pursuit for seismic trace decomposition. J. Geophys. Eng. 2017, 14, 90–99. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, X.; Liu, C.; Chen, C.; Li, X.; Zhang, Y. Seismic matching pursuit decomposition based on the attenuated Ricker wavelet dictionary. In Proceedings of the 79th EAGE Conference and Exhibition 2017, Paris, France, 12–15 June 2017. [Google Scholar]
- Li, J.; Liu, C.; Zeng, Z.; Chen, L. GPR Signal Denoising and Target Extraction With the CEEMD Method. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1615–1619. [Google Scholar]
- Lu, Q.; Liu, C.; Zeng, Z.; Li, J.; Zhang, X. Detection of human’s motions through a wall using UWB radar. In Proceedings of the 2016 16th International Conference on Ground Penetrating Radar (GPR), Hong Kong, China, 13–16 June 2016; pp. 1–4. [Google Scholar]
- Chen, Y.; Ma, J. Random noise attenuation by f-x empirical-mode decomposition predictive filtering. Geophysics 2014, 79, V81–V91. [Google Scholar] [CrossRef]
- Qin, Y.; Qiao, L.H.; Ren, X.Z.; Wang, Q.F. Using bidimensional empirical mode decomposition method to identification buried objects from GPR B-scan image. In Proceedings of the 2016 16th International Conference on Ground Penetrating Radar (GPR), Hong Kong, China, 13–16 June 2016; pp. 1–5. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Liu, W.; Cao, S.; Chen, Y. Applications of variational mode decomposition in seismic time-frequency analysis. Geophysics 2016, 81, V365–V378. [Google Scholar] [CrossRef]
- Liu, W.; Cao, S.; Wang, Z.; Kong, X.; Chen, Y. Spectral Decomposition for Hydrocarbon Detection Based on VMD and Teager-Kaiser Energy. IEEE Geosci. Remote Sens. Lett. 2017, 14, 539–543. [Google Scholar] [CrossRef]
- Liu, W.; Cao, S.; Wang, Z. Application of variational mode decomposition to seismic random noise reduction. J. Geophys. Eng. 2017, 14, 888–899. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Hestenes, M.R. Multiplier and gradient methods. J. Optim. Theory Appl. 1969, 4, 303–320. [Google Scholar] [CrossRef]
- Taner, M.; Koehler, F.; Sheriff, R. Complex seismic trace analysis. Geophysics 1979, 44, 1041–1063. [Google Scholar] [CrossRef]
- Herrera, R.H.; Tary, J.B.; van der Baan, M. Time-frequency representation of microseismic signals using the synchrosqueezing transform. In Proceedings of the GeoConvention 2013, Integration, Calgary, AB, Canada, 6–12 May 2013. [Google Scholar]
- Fomel, S. Seismic data decomposition into spectral components using regularized nonstationary autoregression. Geophysics 2013, 78, O69–O76. [Google Scholar] [CrossRef]
- Rodríguez, A.; Salazar, A.; Vergara, L. Analysis of split-spectrum algorithms in an automatic detection framework. Signal Process. 2012, 92, 2293–2307. [Google Scholar] [CrossRef]

















© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Nilot, E.; Feng, X.; Ren, Q.; Zhang, Z. IMF-Slices for GPR Data Processing Using Variational Mode Decomposition Method. Remote Sens. 2018, 10, 476. https://doi.org/10.3390/rs10030476
Zhang X, Nilot E, Feng X, Ren Q, Zhang Z. IMF-Slices for GPR Data Processing Using Variational Mode Decomposition Method. Remote Sensing. 2018; 10(3):476. https://doi.org/10.3390/rs10030476
Chicago/Turabian StyleZhang, Xuebing, Enhedelihai Nilot, Xuan Feng, Qianci Ren, and Zhijia Zhang. 2018. "IMF-Slices for GPR Data Processing Using Variational Mode Decomposition Method" Remote Sensing 10, no. 3: 476. https://doi.org/10.3390/rs10030476
APA StyleZhang, X., Nilot, E., Feng, X., Ren, Q., & Zhang, Z. (2018). IMF-Slices for GPR Data Processing Using Variational Mode Decomposition Method. Remote Sensing, 10(3), 476. https://doi.org/10.3390/rs10030476