Improving the Remote Sensing Retrieval of Phytoplankton Functional Types (PFT) Using Empirical Orthogonal Functions: A Case Study in a Coastal Upwelling Region
Abstract
:1. Introduction
2. Data and Methodology
2.1. Satellite Data and In Situ Measurements
2.2. The PHYSAT Regional Model for the Coastal Upwelling System Off of Central Chile
2.3. Singular Value Decomposition (SVD) in Spectral Orthogonal Modes: The PHYSTWO Approach
2.4. The Synthetic Matrix of Typical nLw Values for PFT Categories and PFT Estimation from Orthogonal Models
2.5. The Adjustment of PFT Orthomodels with In Situ Data
2.5.1. Diatoms and Nanoeukaryotes
2.5.2. Phaeocystis
2.5.3. Prochlorococcus and Synechococcus
2.6. PFT Estimation with Adjusted Orthomodels
3. Results
3.1. Adaptation of PHYSAT to Upwelling Conditions
3.2. First Spectral Mode and Satellite Chl-a
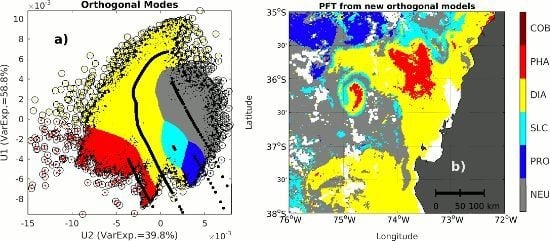
3.3. Use of the Second Spectral Mode for Analyzing PFT Spatial Succession
3.4. PFT Accuracy for the PHYSAT and PHYSTWO Methods
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. The R Matrix
Appendix B. The Unadjusted Synthetic Matix

References
- IOCCG. Phytoplankton Functional Types from Space; Sathyendranath, S., Ed.; Reports of the International Ocean-Colour Coordinating Group; IOCCG: Dartmouth, NS, Canada, 2014; Volume 15. [Google Scholar]
- Bracher, A.; Vountas, M.; Dinter, T.; Burrows, J.P.; Röttgers, R.; Peeken, I. Quantitative observation of cyanobacteria and diatoms from space using PhytoDOAS on SCIAMACHY data. Biogeosciences 2009, 6, 751–764. [Google Scholar] [CrossRef]
- Quéré, C.L.; Harrison, S.P.; Colin Prentice, I.; Buitenhuis, E.T.; Aumont, O.; Bopp, L.; Claustre, H.; Cotrim Da Cunha, L.; Geider, R.; Giraud, X.; et al. Ecosystem dynamics based on plankton functional types for global ocean biogeochemistry models. Glob. Chang. Biol. 2005, 11, 2016–2040. [Google Scholar] [CrossRef]
- Litchman, E.; Klausmeier, C.A. Trait-Based Community Ecology of Phytoplankton. Annu. Rev. Ecol. Evol. Syst. 2008, 39, 615–639. [Google Scholar] [CrossRef]
- Sieburth, J.M.; Smetacek, V.; Lenz, J. Pelagic ecosystem structure: Heterotrophic compartments of the plankton and their relationship to plankton size fractions 1. Limnol. Oceanogr. 1978, 23, 1256–1263. [Google Scholar] [CrossRef]
- Finkel, Z.V.; Beardall, J.; Flynn, K.J.; Quigg, A.; Rees, T.A.V.; Raven, J.A. Phytoplankton in a changing world: Cell size and elemental stoichiometry. J. Plankton Res. 2010, 32, 119–137. [Google Scholar] [CrossRef]
- Follows, M.J.; Dutkiewicz, S. Modeling Diverse Communities of Marine Microbes. Annu. Rev. Mar. Sci. 2011, 3, 427–451. [Google Scholar] [CrossRef] [PubMed]
- Nair, A.; Sathyendranath, S.; Platt, T.; Morales, J.; Stuart, V.; Forget, M.-H.; Devred, E.; Bouman, H. Remote sensing of phytoplankton functional types. Remote Sens. Environ. 2008, 112, 3366–3375. [Google Scholar] [CrossRef]
- Aiken, J.; Pradhan, Y.; Barlow, R.; Lavender, S.; Poulton, A.; Holligan, P.; Hardman-Mountford, N. Phytoplankton pigments and functional types in the Atlantic Ocean: A decadal assessment, 1995–2005. Deep Sea Res. Part II Top. Stud. Oceanogr. 2009, 56, 899–917. [Google Scholar] [CrossRef]
- Mouw, C.B.; Hardman-Mountford, N.J.; Alvain, S.; Bracher, A.; Brewin, R.J.W.; Bricaud, A.; Ciotti, A.M.; Devred, E.; Fujiwara, A.; Hirata, T.; et al. A Consumer’s Guide to Satellite Remote Sensing of Multiple Phytoplankton Groups in the Global Ocean. Front. Mar. Sci. 2017, 4. [Google Scholar] [CrossRef]
- Bracher, A.; Bouman, H.A.; Brewin, R.J.W.; Bricaud, A.; Brotas, V.; Ciotti, A.M.; Clementson, L.; Devred, E.; Di Cicco, A.; Dutkiewicz, S.; et al. Obtaining Phytoplankton Diversity from Ocean Color: A Scientific Roadmap for Future Development. Front. Mar. Sci. 2017, 4. [Google Scholar] [CrossRef]
- Chase, A.; Boss, E.; Zaneveld, R.; Bricaud, A.; Claustre, H.; Ras, J.; Dall’Olmo, G.; Westberry, T.K. Decomposition of in situ particulate absorption spectra. Methods Oceanogr. 2013, 7, 110–124. [Google Scholar] [CrossRef]
- Werdell, P.J.; Roesler, C.S.; Goes, J.I. Discrimination of phytoplankton functional groups using an ocean reflectance inversion model. Appl. Opt. 2014, 53, 4833–4849. [Google Scholar] [CrossRef] [PubMed]
- Uitz, J.; Stramski, D.; Reynolds, R.A.; Dubranna, J. Assessing phytoplankton community composition from hyperspectral measurements of phytoplankton absorption coefficient and remote-sensing reflectance in open-ocean environments. Remote Sens. Environ. 2015, 171, 58–74. [Google Scholar] [CrossRef]
- Di Cicco, A.; Sammartino, M.; Marullo, S.; Santoleri, R. Regional Empirical Algorithms for an Improved Identification of Phytoplankton Functional Types and Size Classes in the Mediterranean Sea Using Satellite Data. Front. Mar. Sci. 2017, 4. [Google Scholar] [CrossRef]
- Sammartino, M.; Di Cicco, A.; Marullo, S.; Santoleri, R. Spatio-temporal variability of micro-, nano- and pico-phytoplankton in the Mediterranean Sea from satellite ocean colour data of SeaWiFS. Ocean Sci. Discuss. 2015, 12, 161–201. [Google Scholar] [CrossRef]
- Brotas, V.; Brewin, R.J.W.; Sá, C.; Brito, A.C.; Silva, A.; Mendes, C.R.; Diniz, T.; Kaufmann, M.; Tarran, G.; Groom, S.B.; et al. Deriving phytoplankton size classes from satellite data: Validation along a trophic gradient in the eastern Atlantic Ocean. Remote Sens. Environ. 2013, 134, 66–77. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Sathyendranath, S.; Lange, P.K.; Tilstone, G. Comparison of two methods to derive the size-structure of natural populations of phytoplankton. Deep Sea Res. Part Oceanogr. Res. Pap. 2014, 85, 72–79. [Google Scholar] [CrossRef]
- Laney, S.R.; Sosik, H.M. Phytoplankton assemblage structure in and around a massive under-ice bloom in the Chukchi Sea. Deep Sea Res. Part II Top. Stud. Oceanogr. 2014, 105, 30–41. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Hardman-Mountford, N.J.; Lavender, S.J.; Raitsos, D.E.; Hirata, T.; Uitz, J.; Devred, E.; Bricaud, A.; Ciotti, A.; Gentili, B. An intercomparison of bio-optical techniques for detecting dominant phytoplankton size class from satellite remote sensing. Remote Sens. Environ. 2011, 115, 325–339. [Google Scholar] [CrossRef]
- Kostadinov, T.S.; Cabré, A.; Vedantham, H.; Marinov, I.; Bracher, A.; Brewin, R.J.W.; Bricaud, A.; Hirata, T.; Hirawake, T.; Hardman-Mountford, N.J.; et al. Inter-comparison of phytoplankton functional type phenology metrics derived from ocean color algorithms and Earth System Models. Remote Sens. Environ. 2017, 190, 162–177. [Google Scholar] [CrossRef]
- Alvain, S.; Moulin, C.; Dandonneau, Y.; Bréon, F.M. Remote sensing of phytoplankton groups in case 1 waters from global SeaWiFS imagery. Deep Sea Res. Part Oceanogr. Res. Pap. 2005, 52, 1989–2004. [Google Scholar] [CrossRef] [Green Version]
- Dandonneau, Y.; Deschamps, P.-Y.; Nicolas, J.-M.; Loisel, H.; Blanchot, J.; Montel, Y.; Thieuleux, F.; Becu, G. Seasonal and interannual variability of ocean color and composition of phytoplankton communities in the North Atlantic, equatorial Pacific and South Pacific. Deep Sea Res. Part II Top. Stud. Oceanogr. 2004, 51, 303–318. [Google Scholar] [CrossRef] [Green Version]
- Alvain, S.; Moulin, C.; Dandonneau, Y.; Loisel, H. Seasonal distribution and succession of dominant phytoplankton groups in the global ocean: A satellite view. Glob. Biogeochem. Cycles 2008, 22. [Google Scholar] [CrossRef]
- Alvain, S.; Loisel, H.; Dessailly, D. Theoretical analysis of ocean color radiances anomalies and implications for phytoplankton groups detection in case 1 waters. Opt. Express 2012, 20, 1070–1083. [Google Scholar] [CrossRef] [PubMed]
- Siegel, D.A.; Maritorena, S.; Nelson, N.B.; Behrenfeld, M.J. Independence and interdependencies among global ocean color properties: Reassessing the bio-optical assumption. J. Geophys. Res. Oceans 2005, 110, C07011. [Google Scholar] [CrossRef]
- Navarro, G.; Alvain, S.; Vantrepotte, V.; Huertas, I.E. Identification of dominant phytoplankton functional types in the Mediterranean Sea based on a regionalized remote sensing approach. Remote Sens. Environ. 2014, 152, 557–575. [Google Scholar] [CrossRef]
- Catherine, A.; Escoffier, N.; Belhocine, A.; Nasri, A.B.; Hamlaoui, S.; Yéprémian, C.; Bernard, C.; Troussellier, M. On the use of the FluoroProbe®, a phytoplankton quantification method based on fluorescence excitation spectra for large-scale surveys of lakes and reservoirs. Water Res. 2012, 46, 1771–1784. [Google Scholar] [CrossRef] [PubMed]
- Morales, C.E.; Anabalón, V.; Bento, J.P.; Hormazabal, S.; Cornejo, M.; Correa-Ramírez, M.A.; Silva, N. Front-Eddy Influence on Water Column Properties, Phytoplankton Community Structure, and Cross-Shelf Exchange of Diatom Taxa in the Shelf-Slope Area Off Concepción (~36–37°S). J. Geophys. Res. Oceans 2017. [Google Scholar] [CrossRef]
- Böttjer, D.; Morales, C.E. Nanoplanktonic assemblages in the upwelling area off Concepción (∼36°S), central Chile: Abundance, biomass, and grazing potential during the annual cycle. Prog. Oceanogr. 2007, 75, 415–434. [Google Scholar] [CrossRef]
- Collado-Fabbri, S.; Vaulot, D.; Ulloa, O. Structure and seasonal dynamics of the eukaryotic picophytoplankton community in a wind-driven coastal upwelling ecosystem. Limnol. Oceanogr. 2011, 56, 2334–2346. [Google Scholar] [CrossRef]
- Morales, C.E.; Anabalón, V. Phytoplankton biomass and microbial abundances during the spring upwelling season in the coastal area off Concepción, central-southern Chile: Variability around a time series station. Prog. Oceanogr. 2012, 92–95, 81–91. [Google Scholar] [CrossRef]
- Anabalón, V.; Morales, C.E.; González, H.E.; Menschel, E.; Schneider, W.; Hormazabal, S.; Valencia, L.; Escribano, R. Micro-phytoplankton community structure in the coastal upwelling zone off Concepción (central Chile): Annual and inter-annual fluctuations in a highly dynamic environment. Prog. Oceanogr. 2016, 149, 174–188. [Google Scholar] [CrossRef]
- Vogt, M.; O’Brien, C.; Peloquin, J.; Schoemann, V.; Breton, E.; Estrada, M.; Gibson, J.; Karentz, D.; Van Leeuwe, M.A.; Stefels, J.; et al. Global marine plankton functional type biomass distributions: Phaeocystis spp. Earth Syst. Sci. Data 2012, 4, 107–120. [Google Scholar] [CrossRef]
- Peperzak, L.; van der Woerd, H.J.; Timmermans, K.R. Disparities between in situ and optically derived carbon biomass and growth rates of the prymnesiophyte Phaeocystis globosa. Biogeosciences 2015, 12, 1659–1670. [Google Scholar] [CrossRef]
- Gordon, H.R.; Clark, D.K.; Brown, J.W.; Brown, O.B.; Evans, R.H.; Broenkow, W.W. Phytoplankton pigment concentrations in the Middle Atlantic Bight: Comparison of ship determinations and CZCS estimates. Appl. Opt. 1983, 22, 20. [Google Scholar] [CrossRef] [PubMed]
- Morel, A. Optical Modeling of the Upper Ocean in Relation to Its Biogenous. Matter Content (Case I Waters. J. Geophys. Res. 1988, 93, 10749–10768. [Google Scholar] [CrossRef]
- Bjornsson, H.; Venegas, S. A Manual for EOF and SVD Analyses of Climate Data; C2GCR Report Ser.; McGill University: Montreal, QC, Canada, 1997; Volume 97–1, pp. 1–52. [Google Scholar]
- Hutchins, D.A.; Hare, C.E.; Weaver, R.S.; Zhang, Y.; Firme, G.F.; DiTullio, G.R.; Alm, M.B.; Riseman, S.F.; Maucher, J.M.; Geesey, M.E.; et al. Phytoplankton iron limitation in the Humboldt Current and Peru Upwelling. Limnol. Oceanogr. 2002, 47, 997–1011. [Google Scholar] [CrossRef]
- Schoemann, V.; Becquevort, S.; Stefels, J.; Rousseau, V.; Lancelot, C. Phaeocystis blooms in the global ocean and their controlling mechanisms: A review. J. Sea Res. 2005, 53, 43–66. [Google Scholar] [CrossRef]
- Heywood, J.L.; Zubkov, M.V.; Tarran, G.A.; Fuchs, B.M.; Holligan, P.M. Prokaryoplankton standing stocks in oligotrophic gyre and equatorial provinces of the Atlantic Ocean: Evaluation of inter-annual variability. Deep Sea Res. Part II Top. Stud. Oceanogr. 2006, 53, 1530–1547. [Google Scholar] [CrossRef]
- Bibby, T.S.; Zhang, Y.; Chen, M. Biogeography of Photosynthetic Light-Harvesting Genes in Marine Phytoplankton. PLoS ONE 2009, 4, e4601. [Google Scholar] [CrossRef] [PubMed]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. Oceans 1998, 103, 24937–24953. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference: A novel ocean chlorophyll-a algorithm. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Sathyendranath, S.; Hirata, T.; Lavender, S.J.; Barciela, R.M.; Hardman-Mountford, N.J. A three-component model of phytoplankton size class for the Atlantic Ocean. Ecol. Model. 2010, 221, 1472–1483. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Cota, G.; Stuart, V.; Maass, H.; Platt, T. Remote sensing of phytoplankton pigments: A comparison of empirical and theoretical approaches. Int. J. Remote Sens. 2001, 22, 249–273. [Google Scholar] [CrossRef]
- Liu, X.; Huang, B.; Liu, Z.; Wang, L.; Wei, H.; Li, C.; Huang, Q. High-resolution phytoplankton diel variations in the summer stratified central Yellow Sea. J. Oceanogr. 2012, 68, 913–927. [Google Scholar] [CrossRef]
- See, J.H.; Campbell, L.; Richardson, T.L.; Pinckney, J.L.; Shen, R.; Guinasso, N.L. Combining new technologies for determination of phytoplankton community structure in the northern Gulf of Mexico 1: Phytoplankton community structure. J. Phycol. 2005, 41, 305–310. [Google Scholar] [CrossRef]
- Escoffier, N.; Bernard, C.; Hamlaoui, S.; Groleau, A.; Catherine, A. Quantifying phytoplankton communities using spectral fluorescence: The effects of species composition and physiological state. J. Plankton Res. 2015, 37, 233–247. [Google Scholar] [CrossRef]















| Method | Retrievals | % Ret. 1 | NEU (%) | PRO (%) | SLC (%) | DIA (%) | PHA (%) | COB (%) |
|---|---|---|---|---|---|---|---|---|
| PHYSAT nLwref | 18,944 | 26.9 | 16.1 | 3.1 | 3.3 | 3.0 | 1.4 | 0.0 |
| PHYSAT nLwupw | 27,874 | 39.5 | 11.9 | 10.1 | 7.1 | 10.3 | 0.2 | 0.0 |
| PHYSTWO unadj. | 70,009 | 99.3 | 18.6 | 35.4 | 22.6 | 10.1 | 11.5 | 0.0 |
| PHYSTWO adj. | 70,009 | 99.3 | 37.7 | 8.9 | 8.6 | 38.4 | 5.7 | 0.0 |
| Chl-FP | Chl-sat | U1 | U2 | |
|---|---|---|---|---|
| CDOM-FP | −0.29 S | - | - | - |
| CDOM-20m | - | −0.14 NS | −0.11 NS | 0.22 NS |
| Method | NEU | DIA | PRO | SLC | ||||
|---|---|---|---|---|---|---|---|---|
| Ret.(1) | % Agr. | Ret. | % Agr | Ret. | %PAgr. | Ret. | %PAgr. | |
| PHYSAT nLwref | 64 | 6.1 | 0 | 0.0 | 2169 | 10.3 | 2305 | 9.7 |
| PHYSAT nLwuwp | 56 | 0.0 | 9 | 1.9 | 7111 | 13.8 | 5028 | 8.0 |
| PHYSTWO unadj. | 73 | 0.0 | 93 | 19.7 | 24,975 | 55.7 | 15,955 | 11.9 |
| PHYSTWO adj. | 174 | 81.6 | 327 | 68.9 | 6289 | 29.9 | 6051 | 22.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Correa-Ramirez, M.; Morales, C.E.; Letelier, R.; Anabalón, V.; Hormazabal, S. Improving the Remote Sensing Retrieval of Phytoplankton Functional Types (PFT) Using Empirical Orthogonal Functions: A Case Study in a Coastal Upwelling Region. Remote Sens. 2018, 10, 498. https://doi.org/10.3390/rs10040498
Correa-Ramirez M, Morales CE, Letelier R, Anabalón V, Hormazabal S. Improving the Remote Sensing Retrieval of Phytoplankton Functional Types (PFT) Using Empirical Orthogonal Functions: A Case Study in a Coastal Upwelling Region. Remote Sensing. 2018; 10(4):498. https://doi.org/10.3390/rs10040498
Chicago/Turabian StyleCorrea-Ramirez, Marco, Carmen E. Morales, Ricardo Letelier, Valeria Anabalón, and Samuel Hormazabal. 2018. "Improving the Remote Sensing Retrieval of Phytoplankton Functional Types (PFT) Using Empirical Orthogonal Functions: A Case Study in a Coastal Upwelling Region" Remote Sensing 10, no. 4: 498. https://doi.org/10.3390/rs10040498
APA StyleCorrea-Ramirez, M., Morales, C. E., Letelier, R., Anabalón, V., & Hormazabal, S. (2018). Improving the Remote Sensing Retrieval of Phytoplankton Functional Types (PFT) Using Empirical Orthogonal Functions: A Case Study in a Coastal Upwelling Region. Remote Sensing, 10(4), 498. https://doi.org/10.3390/rs10040498