A Hybrid Color Mapping Approach to Fusing MODIS and Landsat Images for Forward Prediction

Abstract

We present a simple, and efficient approach to fusing MODIS and Landsat images. It is well known that MODIS images have high temporal resolution and low spatial resolution, whereas Landsat images are just the opposite. Similar to earlier approaches, our goal is to fuse MODIS and Landsat images to yield high spatial and high temporal resolution images. Our approach consists of two steps. First, a mapping is established between two MODIS images, where one is at an earlier time, t₁, and the other one is at the time of prediction, t_p. Second, this mapping is applied to map a known Landsat image at t₁ to generate a predicted Landsat image at t_p. Similar to the Spatial and Temporal Adaptive Reflectance Fusion Model (STARFM), SpatioTemporal Image-Fusion Model (STI-FM), and the Flexible Spatiotemporal DAta Fusion (FSDAF) approaches, only one pair of MODIS and Landsat images is needed for prediction. Using seven performance metrics, experiments involving actual Landsat and MODIS images demonstrated that the proposed approach achieves comparable or better fusion performance than that of STARFM, STI-FM, and FSDAF.

1. Introduction

Fusing high spatial resolution/low temporal resolution Landsat images with low spatial resolution/high temporal resolution MODIS images will have many applications, such as drought monitoring, fire damage assessment, flood damage monitoring, etc. In [1], a fusion approach known as Spatial and Temporal Adaptive Reflectance Fusion Model (STARFM) was proposed and demonstrated. The STARFM has been used to generate daily time-series vegetation index and evapotranspiration for crop condition and drought monitoring [1,2]. Several alternative algorithms [3,4] were published to further improve the fusion performance. The Bayesian prediction approach [5,6,7], which was also proposed for fusing satellite images with complementary characteristics, can be an alternative fusion method for Landsat and MODIS. According to the survey paper [8], the STAARCH [3] approach can handle abrupt changes, but requires two pairs of MODIS and Landsat images. The ESTARFM [4] algorithm focuses on enhancing the performance of mixed pixels. Similar to STAARCH, ESTARFM also requires two pairs of images. As a result, both STAARCH and ESTARFM may not be suitable for forward prediction.

Recently, the Flexible Spatiotemporal DAta Fusion (FSDAF) algorithm can use one pair of MODIS and Landsat images for forward prediction [9]. The method has six steps, including land cover classification, grouping of neighboring pixels, etc. The computational load is heavy, as one prediction may take more than one hour to finish for an image size of 1200 × 1200. Moreover, since there are multiple steps in the prediction process, it is hard to grasp which step contributes the most to the prediction performance. A relatively simple and more efficient algorithm, the SpatioTemporal Image-Fusion Model (STI-FM) [10] applies clustering to the images first, and, for each cluster, performs a separate prediction. In addition to the above algorithms, some alternative fusion ideas [11,12,13,14,15,16] were proposed and evaluated. Interested readers can find concise reviews for these alternative methods in [10]. In this paper, we present a simple approach to fusing MODIS and Landsat images for forward prediction. Our approach was motivated by our recent pansharpening work for synthesizing a high resolution hyperspectral image by fusing a high resolution color image with a low resolution hyperspectral image cube [17]. Our approach is called hybrid color mapping (HCM), which has also been applied to enhance Mastcam images [18] in the Curiosity rover and Mars satellite imagers THEMIS and TES [19]. The HCM is simple, intuitive, and computationally efficient, as compared to other algorithms in the literature. Most importantly, it has high performance because numerous recent comparative studies [18,19,20] have demonstrated its efficacy. Similar to STARFM, STI-FM, and FSDAF, only one pair of MODIS and Landsat images is needed for prediction.

Our paper is organized as follows. Section 2 introduces our approach. Section 3 presents the experimental results. Two types of real images have been used. One type is homogeneous and the other is the more challenging type of heterogeneous images. Discussions are included in Section 4. Finally, the conclusions and future directions are given in Section 5.

2. Materials and Methods

Our approach is simple, intuitive, and has two steps. First, a mapping is established between two MODIS images where one is at an earlier time, t₁, and the other one is at the time of prediction, t_p. To achieve better prediction results, it is necessary to divide the images into small patches, which can be either overlapping or non-overlapping. The mapping is then obtained for each patch. It should be noted that the mapping is between a pixel vector in one image and another pixel vector in another image. Second, this mapping is applied to a known Landsat image at t₁ to generate a predicted Landsat image at t_p.

2.1. A Simple Motivating Example of Our Approach

We will use one band of MODIS and LANDSAT to illustrate our approach. Figure 1 shows two pairs of MODIS (M1 and M2) and Landsat (L1 and L2) images. The pairs, (M1, L1) and (M2, L2) were collected on the same days. From Figure 1, we have two observations. First, the MODIS images can be treated as blurred versions of their Landsat counterparts. Second, the intensity relationship between the MODIS pixels is somewhat similar to that of those Landsat pixels. For example, the middle of L1 is darker than the rest of the scene, and this can be easily seen in M1 as well. Similarly, the middle part of L2 is slightly brighter than the rest and one can see the same in M2. The above observations indicate that the heterogeneous landscape information is captured in the MODIS images. If we can capture the intensity mapping between the MODIS images at two different times, then we can use that mapping to predict the Landsat image at time $t_p$ using Landsat image at $t_k$. It turns out that, although the above idea is simple and intuitive, the prediction results using this idea are quite accurate in previous experiments [19,20].

To further substantiate the above observations, we include some statistics (

Table 1. Mean and standard deviation of MODIS and Landsat images at different dates.

Day 128			Day 144
	Mean	Standard Deviation		Mean	Standard Deviation
MODIS	0.085	0.057	MODIS	0.090	0.064
Landsat	0.089	0.058	Landsat	0.090	0.066
Day 214			Day 246
	Mean	Standard Deviation		Mean	Standard Deviation
MODIS	0.137	0.149	MODIS	0.135	0.124
Landsat	0.139	0.155	Landsat	0.133	0.125

) from four pairs of MODIS and Landsat images. Days 128 and 144 belong to homogeneous regions and Days 214 and 246 are heterogeneous regions. It can be easily seen that the means and the standard deviations of MODIS and Landsat images are indeed very close, corroborating the visual observations in Figure 1.

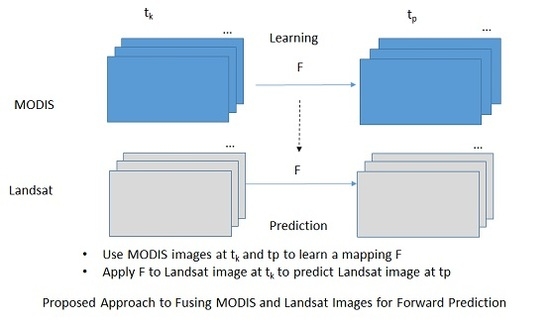
2.2. Proposed Approach Based on Hybrid Color Mapping (HCM)

Figure 2 illustrates our proposed prediction approach. Based on the available MODIS images that were collected at $t_k$ and $t_p$, we learn the pixel by pixel mapping between the two images. The learned matrix F is then applied in the prediction step. Using similar notations in related work [1], the prediction of Landsat image at $t_p$ can be achieved by

$$L(x,y,t_p)=F\times L(x,y,t_k)$$

(1)

where $L(·,·,·)$ denotes a pixel vector (up to Q with Q being the number of bands) for this application and $F$ is a pixel to pixel mapping/transformation matrix with appropriate dimensions. $F$ can be determined by using the following relationship

$$M(x,y,t_p)=F\times M(x,y,t_k)$$

(2)

where $M(·,·,·)$ denotes a pixel vector (Q bands). To account for the intensity differences between two images, a variant of (2) can be described as

$$M(x,y,t_p)=F_1\times M(x,y,t_k)+F_2$$

(3)

where $F_2$ is a vector of constants.

With no loss of generality, let us focus on the determination of F in (2). Now, let us denote $Y_{t_p}$ as the set of all of the multispectral pixels $M(x,y,t_p)\in R^Q$ for all the pixels in the image at $t_p$ and $Y_{t_k}$ as the set of all the multispectral pixels $M(x,y,t_k)\in R^Q$ in the image at $t_k$. Q is the number of bands. Since $M(x,y,t_p)$ and $M(x,y,t_k)$ are vectors, $Y_{t_p}$ and $Y_{t_k}$ can be expressed as

$$Y_{t_p}=\left[\begin{array}{cccc}M(1,1,t_p)& \dots & \dots & M(N_R,N_C,t_p)\end{array}\right]$$

(4)

$$Y_{t_k}=\left[\begin{array}{cccc}M(1,1,t_p)& \dots & \dots & M(N_R,N_C,t_k)\end{array}\right]$$

(5)

where $N_R$ and $N_C$ are the numbers of rows and columns, respectively.

We call the mapping F in (2) the global version and all of the pixels in $Y_{t_k}$ and $Y_{t_p}$ are used in estimating F. To estimate F, we will use the least square approach, which minimizes the error

$$E={\displaystyle \sum _{x=1}^{N_R}{\displaystyle \sum _{y=1}^{N_C}P{(x,y)}^{\mathrm{Transpose}}P(x,y)}}$$

(6)

where $P(x,y)=M(x,y,t_p)-FM(x,y,t_k)$.

Following the definition of Frobenius norm [21], (6) is equivalent to

$$E=\left|\right|Y_{t_p}-F{Y}_{t_k}|{|}_F^2$$

(7)

Solving F in (7) involves the following. Since

$$\begin{gathered} E=\left|\right|Y_{t_p}-F{Y}_{t_k}|{|}_F^2=tr((Y_{t_p}-F{Y}_{t_k}){(Y_{t_p}-F{Y}_{t_k})}^T) \\ =tr[Y_{t_p}{Y}_{t_p}{}^T]-tr[Y_{t_p}{Y}_{t_k}{}^T{F}^T]-tr[F{Y}_{t_k}{Y}_{t_p}{}^T]+tr[F{Y}_{t_k}{Y}_{t_k}{}^T{F}^T]. \end{gathered}$$

(8)

Differentiating (8) with respect to F yields [22]

$$\frac{\partial E}{\partial F}=-2Y_{t_p}{Y}_{t_k}{}^T+2F{Y}_{t_k}{Y}_{t_k}{}^T$$

(9)

Setting the above to zero will yield

$$F^{\ast }=Y_{t_p}{Y}_{t_k}{}^T{(Y_{t_k}{Y}_{t_k}{}^T)}^{-1}$$

(10)

Unlike normal image mapping, such as the 3 × 3 image transform matrices (a rotation or perspective transformation), which maps between the spatially distributed patches, it should be noted that F is a pixel to pixel mapping between two multispectral pixels.

To avoid instability, we can add a regularization term in (7). That is,

$$F^{\ast }=\underset{F}{\arg \min }||Y_{t_p}-F{Y}_{t_k}|{|}_F+\lambda ||F|{|}_F$$

(11)

where $\lambda$ is a regularization parameter and the optimal F becomes

$$F^{\ast }=Y_{t_p}{Y}_{t_k}{}^T{(Y_{t_k}{Y}_{t_k}{}^T+\lambda I)}^{-1}$$

(12)

with I an identity matrix with the same dimension as $Y_{t_k}{Y}_{t_k}{}^T$.

Remark 1.

Difference between the HCM in this paper and the HCM in [17].

Although the mathematical derivations are the same, the proposed HCM in this paper is different from that in [17]. The key difference is the implementation. In [17], the mapping is between a downsampled high resolution image and a low resolution hyperspectral image, whereas here the mapping is between two low resolution MODIS images.

Remark 2.

Addition of a bias term.

If the means of the two MODIS images are different, we can easily extend the above derivation to arrive at a new expression for $F_1$ and $F_2$ in (3). This can be done by rewriting (3) as

$$\begin{array}{ll}M(x,y,t_p)& =\left[\begin{array}{cc}{F}_1& F_2\end{array}\right]{\left[\begin{array}{cc}M(x,y,t_k)& 1\end{array}\right]}^T\\ & =F_{\mathrm{a}}\times M_{\mathrm{a}}\end{array}$$

(13)

that is, we simply augment the vector M by one more row of 1. After that, the derivation will be the same as before.

Remark 3.

Local Mapping.

Based on our observations in some cases, prediction results will be more accurate if we divide the images into patches. Each patch will have its own mapping matrix. Figure 3 illustrates the local prediction approach. The patches can be overlapped or non-overlapped. In this paper, overlapped patches were used for homogeneous areas and non-overlapped patches were used for the heterogeneous areas.

Remark 4.

Band by band mapping.

It should be noted that the derivations for the forward prediction are done jointly for all of the bands. Actually, the mapping can also be done band by band.

Remark 5.

Only one pair of MODIS and Landsat images.

Unlike STAARCH and ESTARFM, our approach does not require two pairs of MODIS and Landsat images for prediction. This will be ideal for forward prediction, where only past measurements of Landsat images are available.

Remark 6.

One mapping per cluster.

One can also perform image clustering/segmentation first and then use HCM for each individual cluster. We implemented this approach and the results are similar to that of the non-clustering approach. Discussions on this clustering approach will be summarized in Section 4.

2.3. Evaluation Metrics

We evaluate the performance of algorithms using the following seven objective metrics. Moreover, computational times are also used in our comparative studies.

• Absolute Difference (AD). The AD of two vectorized images $S$ (ground truth) and $\widehat{S}$ (prediction) is defined as

  $$\mathrm{AD}(S,\widehat{S})=\frac{1}{Z}{\displaystyle \sum _{j=1}^Z\left|s_j-{\widehat{s}}_j\right|}$$

  (14)

  where Z is the number of pixels in each image. The ideal value of AD is 0 if the prediction is perfect.
• RMSE (Root Mean Squared Error). The RMSE of two vectorized images $S$ (ground truth) and $\widehat{S}$ (prediction) is defined as

  $$\mathrm{RMSE}(S,\widehat{S})=\sqrt{\frac{1}{Z}{\displaystyle \sum _{j=1}^Z{\left(s_j-{\widehat{s}}_j\right)}^2}}$$

  (15)

  where Z is the number of pixels in each image. The ideal value of RMSE is 0 if the prediction is perfect.
• CC (Cross-Correlation). We used the codes from Open Remote Sensing website (https://openremotesensing.net/). The ideal value of CC is 1 if the prediction is perfect.
• ERGAS (Erreur Relative. Globale Adimensionnelle de Synthese). We used the codes from [23]. The ERGAS is defined as

  $$\mathrm{EGARS}(S,\widehat{S})=100d\frac{\mathrm{RMSE}}{\mu }$$

  (16)

  for some constant d depending on the resolution and $\mu$ is the mean the ground truth image. The ideal value of ERGAS is 0 if a prediction algorithm flawlessly reconstructs the Landsat bands.
• SSIM (Structural Similarity). It is a metric to reflect the similarity between two images. An equation of SSIM can be found in [9]. The ideal value of SSIM is 1 for perfect prediction.
• SAM (Spectral Angle Mapper) [23]. The spectral angle mapper measures the angle between two vectors. The ideal value of SAM is 0 for perfect reconstruction.
• Q2n: A definition for Q2n can be found in [24,25]. The ideal value of Q2n is 1. The codes can be downloaded from Open Remote Sensing website.

3. Results

In this section, we present extensive experimental results. Since our main interest is in forward prediction, we only compare with STARFM, STI-FM, and FSDAF.

3.1. Data Set 1: Scene Contents Are Homogeneous

Data set 1 is the Boreal Ecosystem–Atmosphere Study (BOREAS) southern study area (54.6°N, 105.8°W) that has been used by Gao et al. [26] in the data fusion test. This is a relatively homogeneous area. The major land cover type is forest, with subsidiary fen and spare vegetation. Land cover patches are large. Landsat and MODIS data have been reprocessed using the latest available collections when we started this study. Landsat surface reflectance images (L1T) were ordered from U.S. Geological Survey (USGS). MODIS daily surface reflectance products (MOD09GA, Collection 6) [27] were corrected to nadir BRDF-adjusted reflectance (NBAR) using MODIS BRDF products (MCD43A1, Collection 5) [26]. Note that the Collection 6 of daily MODIS NBAR at 500 m resolution is now available and can be directly used. Co-registration between Landsat and MODIS was applied to all of the Landsat-MODIS image pairs using maximum correlation approach [27]. Four Landsat-MODIS image pairs (day 128, 144, 192 and 224) on 2001 were re-processed for the study. Each image has six bands. We can perform six forward prediction experiments.

The parameters of our prediction algorithm for the first data set are as follows. Band to band prediction was used and no bias term was introduced. The images are divided into patches with a patch size of 80 Landsat pixels. The regularization term was chosen to be 0.001. The overlapping window size for patches is 40.

Table 2. Comparison of forward prediction results of using Landsat image 128 to predict Landsat image 144.

					HCM
	AD	RMSE	cc	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.0076	0.01	0.9699	9.71 × 10−8	0.9679	0.4638	0.888	0.836	0.9174
Red	0.0043	0.006	0.9475	1.07 × 10−7	0.9815	1.0247	0.8498
Green	0.0045	0.006	0.9114	1.11 × 10−7	0.9858	0.9485	0.751
Bhie	0.004	0.0052	0.8524	1.06 × 10−7	0.9827	1.1754	0.6183
SW1	0.0068	0.01	0.9814	3.77 × 10−3	0.9712	0.5571	0.9251
SW2	0.0065	0.0094	0.9705	1.48 × 10−1	0.9674	0.9163	0.8817
					STARFM
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.0089	0.0316	0.7645	1.55 × 10−1	0.9593	1.4716	0.8642	0.8152	3.3102
Red	0.0047	0.0172	0.6703	4.49 × 10−2	0.9802	2.9705	0.8474
Green	0.0048	0.0188	0.479	5.43 × 10−2	0.9849	2.9963	0.7551
Bhie	0.0044	0.0185	0.385	5.27 × 10−2	0.9807	4.1505	0.6119
SW1	0.0083	0.0293	0.8614	1.35 × 10−1	0.9635	1.6291	0.9039
SW2	0.0069	0.0253	0.8279	2.25 × 10−1	0.9602	2.4753	0.8641
					FSDAF
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.0086	0.015	0.9266	7.99 × 10−8	0.9599	0.6919	0.8722	0.8197	1.382
Red	0.0048	0.0086	0.8825	8.78 × 10−8	0.9782	1.4573	0.8385
Green	0.0047	0.0084	0.7775	9.21 × 10−8	0.984	1.3224	0.7515
Bhie	0.0047	0.0083	0.6743	8.78 × 10−8	0.9791	1.8207	0.5995
SW1	0.0082	0.015	0.9565	3.64 × 10−3	0.9622	0.8283	0.9114
SW2	0.007	0.0122	0.949	1.31 × 10−1	0.9613	1.178	0.8758
					STI-FM
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.008	0.0113	0.9607	1.02 × 10−7	0.9632	0.5206	0.8806	0.8224	1.1434
Red	0.0045	0.0071	0.9198	1.03 × 10−7	0.9793	1.2185	0.8425
Green	0.0044	0.0066	0.8715	1.20 × 10−7	0.9853	1.0468	0.7574
Bhie	0.004	0.0061	0.7568	1.08 × 10−7	0.9799	1.3997	0.5827
SW1	0.0079	0.0117	0.9741	7.21 × 10−2	0.9641	0.6524	0.9164
SW2	0.0072	0.0107	0.9622	1.95 × 10−1	0.9606	1.0359	0.8716

,

Table 3. Comparison of forward prediction results of using Landsat image 144 to predict Landsat image 192.

					HCM
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N	Overall ERGAS
NIR	0.0149	0.0229	0.9331	1.07 × 10−7	0.908	0.8809	0.7828	0.7238	1.392
Red	0.0053	0.0083	0.8489	1.32 × 10−4	0.9667	1.8552	0.6499
Green	0.0051	0.0074	0.8872	1.08 × 10−7	0.979	1.2187	0.6578
Bhie	0.0041	0.0057	0.7791	1.14 × 10−7	0.9785	1.5306	0.4733
SW1	0.0082	0.0135	0.9604	5.51 × 10−2	0.959	0.8261	0.861
SW2	0.0077	0.0116	0.9299	3.80 × 10−1	0.956	1.4902	0.744
					STARFM
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N	Overall ERGAS
NIR	0.0155	0.0243	0.9249	5.42 × 10−3	0.8963	0.9374	0.7507	0.6566	4.9979
Red	0.0056	0.0168	0.627	3.69 × 10−2	0.9606	3.7372	0.6232
Green	0.005	0.0069	0.9026	1.11 × 10−7	0.9811	1.1404	0.6538
Bhie	0.0042	0.0061	0.785	0.0001	0.977	1.6074	0.4669
SW1	0.0088	0.0315	0.8387	0.1979	0.9526	1.9218	0.8555
SW2	0.014	0.0813	0.4725	1.2764	0.9185	11.3554	0.6756
					FSDAF
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N	Overall ERGAS
NIR	0.0161	0.024	0.9290	8.82 × 10−8	0.8891	0.9228	0.7460	0.7119	1.3660
Red	0.0055	0.0085	0.8465	1.32 × 10−4	0.9645	1.8914	0.6331
Green	0.0052	0.0071	0.8920	9.04 × 10−8	0.9808	1.1767	0.6516
Bhie	0.0049	0.0062	0.7824	9.33 × 10−8	0.9764	1.6191	0.4542
SW1	0.0100	0.0125	0.9652	5.12 × 10−2	0.9558	0.7622	0.8761
SW2	0.0083	0.0111	0.9356	2.35 × 10−1	0.9511	0.7622	0.7733
					STI-FM
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N	Overall ERGAS
NIR	0.0219	0.0403	0.7629	1.15 × 10−7	0.8777	1.5255	0.6898	0.6672	1.9131
Red	0.0059	0.0095	0.7765	1.85 × 10−3	0.9525	2.1092	0.6087
Green	0.0059	0.0096	0.7337	1.17 × 10−7	0.9644	1.5609	0.6051
Bhie	0.0044	0.0078	0.5346	0	0.9622	2.1301	0.4146
SW1	0.0112	0.0230	0.8793	0.0972	0.9362	1.3756	0.8102
SW2	0.0089	0.0147	0.8825	0.3051	0.9379	1.8564	0.7184

and

Table 4. Comparison of forward prediction results of using Landsat image 192 to predict Landsat image 224.

					HCM
	AD	RMSE	cc	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.0078	0.0113	0.9821	1.50 × 10−1	0.9718	0.4632	0.9403	0.8291	0.9943
Red	0.0030	0.0042	0.9395	2.60 × 10−2	0.9848	1.2648	0.8047
Green	0.0026	0.0035	0.9471	7.93 × 10−4	0.9899	0.7675	0.7970
Bhie	0.0030	0.0040	0.8326	1.09 × 10−7	0.9839	1.4608	0.5031
SW1	0.0055	0.0083	0.9828	1.11 × 100	0.9769	0.5793	0.9240
SW2	0.0045	0.0065	0.9748	2.21 × 100	0.9766	0.9337	0.8708
					STARFM
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.0105	0.0414	0.8313	4.24 × 10−1	0.9482	1.7106	0.8982	0.7376	6.9867
Red	0.0038	0.0280	0.4243	1.44 × 10−1	0.9781	8.5351	0.7662
Green	0.0031	0.0164	0.5508	4.63 × 10−2	0.9863	3.6126	0.7692
Bhie	0.0033	0.0062	0.7186	3.44 × 10−3	0.9824	2.1397	0.5094
SW1	0.0165	0.1021	0.5782	2.41 × 100	0.9408	7.8226	0.8298
SW2	0.0102	0.0743	0.458	2.52 × 100	0.9437	11.5312	0.7689
					FSDAF
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.0083	0.0123	0.9787	1.49 × 10−1	0.9651	0.5048	0.9314	0.8027	1.0761
Red	0.0032	0.0045	0.9347	2.08 × 10−2	0.9835	1.3653	0.7770
Green	0.0028	0.0040	0.9314	7.93 × 10−4	0.9886	0.8838	0.7665
Bhie	0.0035	0.0046	0.8392	8.98 × 10−8	0.9808	1.5633	0.4958
SW1	0.0061	0.0093	0.9782	9.56 × 10−1	0.9723	0.6613	0.9089
SW2	0.0050	0.0071	0.9703	2.06 × 100	0.972	0.9996	0.8414
					STI-FM
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.0097	0.0139	0.9728	1.77 × 10−1	0.9576	0.5706	0.9184	0.7565	1.4495
Red	0.0042	0.0056	0.9006	2.60 × 10−2	0.9699	1.6338	0.6923
Green	0.0040	0.0053	0.9097	7.93 × 10−4	0.9767	1.1121	0.6672
Bhie	0.0053	0.0067	0.5534	1.09 × 10−7	0.9572	2.7313	0.2374
SW1	0.0065	0.0096	0.9767	1.18 × 100	0.9696	0.6715	0.9088
SW2	0.0055	0.0081	0.9614	2.22 × 100	0.9656	1.1400	0.8340

summarize the forward prediction results of using Landsat image 128 to predict Landsat image 144, Landsat image 144 to predict Landsat image 192, Landsat image 192 to predict Landsat image 224, respectively. The tables are arranged in a similar manner as that of [9]. The first block of each table compares the source Landsat image and the ground truth Landsat image to be predicted. We have applied cloud masks in calculating those values in the tables. In Table 2, one can see that our prediction results in terms of AD, RMSE, CC, ERGAS, SSIM, and Q2n metrics are better than that of STARFM, STI-FM, and FSDAF in almost all of the bands. In the false color image (formed by treating NIR, Red, and Green as Red, Green, and Blue, respectively) that is shown in Figure 4, if one looks at the zoomed-in area inside the red circles, one can see that our results can recover more fine details as compared to that of STARFM and are comparable to that of FSDAF and STI-FM. From Table 3, it can be seen that our results have similar trends as Table 2. This is reflected in Figure 5, as it can be seen that, inside the red circles, our results can preserve the color information slightly better than that of STARFM and STI-FM, and are comparable to FSDAF. From Table 4, our results also give better performance metrics in almost all of the metrics as compared to those of STARFM, STI-FM, and FSDAF. In Figure 6, one can see that the STARFM image has an area in the center/bottom half (inside the white circle) that seems to have some spectral distortion, while our predicted image looks much more like the actual image. Table 4 also shows that our prediction, especially the NIR band, is a lot closer to the ground truth image.

3.2. Data Set 2: Scene Contents Are Heterogeneous

Data set 2 is a rain-fed agricultural area in central Iowa (42.4°N, 93.4°W). The major crops were corn and soybean. They were planted at different times and had different crop phenology. This is a relatively heterogeneous area. Same data processing procedures that were used in Data set 1 were applied. Three Landsat-MODIS image pairs (day 144, 182, and 224) on 2002 were processed.

MODIS daily NBAR were resampled to match Landsat 30 m resolution using the bi-linear interpolation approach. Both data sets have the image size of 1200 by 1200. For each time, one image-pair was used to predict Landsat observation for another pair date and then compared to the actual Landsat reflectance. There are three pairs of MODIS and Landsat images in this data set. Each image has six bands. We can perform two forward prediction experiments.

The parameters of our prediction algorithm for the second data set are as follows. The learning and prediction were performed band by band. For heterogeneous contents, we observed that we need to pick small patch sizes in order to achieve good prediction performance. Patches with a size of two were used and there is no overlapping between the patches. The regularization term was chosen to be 0.001.

Table 5. Comparison of forward prediction results of using Landsat image 182 to predict Landsat image 214.

				HCM
	AD	RMSE	cc	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.0740	0.0945	0.2210	9.98 × 10−8	0.4816	1.8595	0.2341	0.5901	3.4322
Red	0.0119	0.0175	0.6700	1.04 × 10−7	0.8732	5.1146	0.4439
Green	0.0093	0.0116	0.7712	1.04 × 10−7	0.9441	2.3015	0.4824
Bhie	0.0095	0.0119	0.7846	1.24 × 10−7	0.8984	4.9286	0.2943
SW1	0.0212	0.0283	0.7789	2.73 × 10−3	0.8565	1.2631	0.6754
SW2	0.0221	0.0288	0.6564	5.73 × 10−3	0.8198	3.1785	0.4630
				STARFM
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.0650	0.0857	0.2737	5.39 × 10−2	0.5057	1.6615	0.1906	0.5031	11.5752
Red	0.0182	0.0803	0.1716	1.03 × 100	0.8331	24.7442	0.4145
Green	0.0092	0.0232	0.4432	5.62 × 10−2	0.9426	4.3045	0.5394
Bhie	0.0085	0.0226	0.3576	5.74 × 10−2	0.9261	7.2917	0.4620
SW1	0.0236	0.0434	0.6450	1.35 × 10−1	0.8358	1.9414	0.6305
SW2	0.0312	0.0794	0.3244	7.93 × 10−1	0.7151	8.6564	0.3562
				FSDAF
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.0572	0.0732	0.4771	8.12 × 10−8	0.5774	1.4157	0.261	0.6253	3.0218
Red	0.0129	0.0190	0.6737	8.61 × 10−8	0.8503	5.1000	0.4873
Green	0.0090	0.0113	0.7889	8.36 × 10−8	0.9444	2.1736	0.5351
Bhie	0.0068	0.0089	0.7962	1.05 × 10−7	0.9475	2.6787	0.5365
SW1	0.0220	0.0291	0.7705	1.82 × 10−3	0.8482	1.3084	0.6457
SW2	0.0274	0.0342	0.5922	2.60 × 10−3	0.7486	3.6338	0.4224
				STI-FM
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.0623	0.0791	0.2939	9.51 × 10−8	0.5474	1.5191	0.1750	0.4610	3.1275
Red	0.0110	0.0199	0.4640	1.10 × 10−7	0.8718	5.2349	0.2323
Green	0.0084	0.0131	0.6456	1.27 × 10−7	0.9370	2.2967	0.3297
Bhie	0.0091	0.0134	0.6248	1.15 × 10−7	0.9031	5.4819	0.1646
SW1	0.0174	0.0245	0.7495	2.60 × 10−3	0.8791	1.0360	0.6897
SW2	0.0145	0.0277	0.5489	5.21 × 10−3	0.8400	2.9161	0.3632

summarizes the forward prediction results from Landsat image 182 to Landsat image 214. It can be seen that FSDAF has the best performance, followed by STI-FM, HCM, and STARFM. In terms of subjective comparisons, one can see from the false color image in Figure 7, which is created by using the order of near infrared (NIR), red, and green bands, as the RGB bands, that our results are slightly closer to the ground truth image in terms of color.

Table 6. Comparison of forward prediction results of using Landsat image 214 to predict Landsat image 246.

					HCM
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.0257	0.0353	0.8700	1.06 × 10−7	0.8437	0.7735	0.7937	0.7732	1.9607
Red	0.0107	0.0167	0.7977	1.05 × 10−7	0.9140	3.4840	0.6125
Green	0.0087	0.0126	0.7876	1.13 × 10−7	0.9476	1.9139	0.5692
Bhie	0.0046	0.0070	0.8804	1.12 × 10−7	0.9743	1.8618	0.7254
SW1	0.0113	0.0170	0.8793	3.64 × 10−3	0.9364	0.7327	0.8441
SW2	0.0112	0.0175	0.8456	9.11 × 10−3	0.9246	1.6148	0.7769
					STARFM
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Overall Q2N Overall ERGAS
NIR	0.0306	0.0539	0.7734	1.44 × 10−1	0.8176	1.1639	0.7522	0.7701	4.3193
Red	0.0091	0.0306	0.4349	1.16 × 10−1	0.9419	5.4824	0.6861
Green	0.0087	0.0296	0.3512	1.15 × 10−1	0.9606	4.0248	0.6216
Bhie	0.0049	0.0279	0.3113	1.15 × 10−1	0.9772	6.7902	0.7572
SW1	0.0117	0.0375	0.6222	1.45 × 10−1	0.9353	1.5759	0.8376
SW2	0.0111	0.0357	0.5597	1.46 × 10−1	0.9271	3.1603	0.7723
					FSDAF
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Q Overall	Overall ERGAS
NIR	0.0261	0.0358	0.8756	8.70 × 10−8	0.848	0.7723	0.7903	0.7823	1.3975
Red	0.0080	0.0119	0.8325	8.64 × 10−8	0.9455	2.1292	0.6969
Green	0.0073	0.0096	0.8285	9.36 × 10−8	0.9635	1.3114	0.6521
Bhie	0.0048	0.0068	0.8908	9.50 × 10−8	0.9758	1.5796	0.7368
SW1	0.0105	0.0160	0.8771	1.17 × 10−3	0.9383	0.6711	0.8502
SW2	0.0101	0.0158	0.8450	4.69 × 10−3	0.9315	1.3832	0.7875
					STI-FM
	AD	RMSE	CC	SAM	SSIM	ERGAS	Q2N	Q Overall	Overall ERGAS
NIR	0.0268	0.0364	0.8540	1.08 × 10−7	0.8398	0.7923	0.7766	0.7489	1.5995
Red	0.0095	0.0136	0.7710	1.18 × 10−7	0.9366	2.4225	0.6135
Green	0.0095	0.0118	0.7414	1.07 × 10−7	0.9567	1.5699	0.5094
Bhie	0.0043	0.0064	0.8785	1.13 × 10−7	0.9784	1.5804	0.7420
SW1	0.0133	0.0180	0.8651	1.30 × 10−3	0.9396	0.7362	0.7986
SW2	0.0106	0.0168	0.8252	5.47 × 10−3	0.9275	1.4820	0.7692

summarizes the prediction results from Landsat image 214 to Landsat image 246. Although our results are comparable to those of STARFM and STI-FM, and slightly inferior to those of FSDAF, the numbers are close. This is also reflected in the images shown in Figure 8 where the predictions results using STARFM, STI-FM, FSDAF, and our approach are all very close visually.

4. Discussions

The STARFM algorithm is the pioneering work on the fusion of MODIS and Landsat images. The FSDAF incorporates land cover classification and some additional processing steps and yields better performance over the STARFM in heterogeneous areas. When comparing the proposed HCM with the FSDAF method, our method is much simpler and efficient. In fact, HCM is comparable to that of STI-FM in terms of computational complexity. One may think that, since the resolution between Landsat and MODIS is 16 to 1, the proposed HCM based mapping may not be effective. It turns out that we have applied HCM to enhance images with even greater resolution differences: Worldview-2 (25 to 1) [20] and THEMIS and TES (30 to 1) [19]. The results in [19,20] as well as the results in this paper clearly demonstrate that the HCM algorithm is a very competitive method for fusing different types of satellite images. More supporting arguments are presented in the following paragraphs.

4.1. Additional Simulation Studies Using Synthetic Data to Address 16:1 Resolution Concern for HCM

To further validate the performance HCM, we have carried out some additional studies. Similar to the FSDAF paper, we used a synthetic data set, as shown in Figure 9 below. There are three areas besides the background, which has a magnitude of 0.5. A small Gaussian noise (0.001) was added to the image. The pixel magnitudes in Landsat image at t1 are as follows: 0.01 in the circle (radius: 56 pixels), 0.3 in the rectangle and the line. The pixel magnitudes in Landsat image at t₂ are: 0.05 in the circle (radius: 72 pixels), 0.2 in the rectangle and the line. The circles in the two Landsat images are to emulate gradual changes (phenology), and the lines and rectangle are to emulate land cover type changes. The MODIS images were generated by averaging 16 × 16 blocks in the Landsat images.

Now, we summarize the prediction results below in Figure 10.

Table 7. Comparison of FSDAF and HCM for the synthetic data.

	RMSE	CC	SAM	SSIM
Landsat 1	0.0850	0.8370	0.0290	0.9190
FSDAF	0.0240	0.9860	0.0050	0.9110
HCM	0.0320	0.9770	0.0110	0.9460

summarizes four performance metrics. It can be seen that the FSDAF results have smaller prediction errors than those of HCM. The HCM results have some blurry peripherals. Because this synthetic data set is somewhat similar to the heterogeneous landscape, the FSDAF method performed well. However, this simple example also substantiates that our HCM does not have any “grave” issues; it just performs slightly worse than FSDAF in the heterogeneous cases. We did not include the STI-FM results here, as thorough comparisons have been carried out earlier in Section 3.

4.2. Performance of HCM for Applications with 25:1 Resolution Difference

To further alleviate the concern that our proposed HCM method may not work for large spatial resolution applications, we would like to mention some of the fusion results where we have 25:1 resolution difference between two images. The 25 to 1 resolution difference application is for enhancing the eight SWIR bands (7.5 m resolution) using the pan band (0.31 m resolution) in Worldview-3 images. A paper has been published [20]. See Table 5 in [20]. It can be seen that our HCM results are slightly better than other state-of-the-art methods in the literature using three performance metrics, even if the resolution difference is 25:1.

4.3. Performance of HCM for Applications with 30:1 Resolution Difference

Here, we mention one more application of HCM to image fusion where the spatial resolution difference between the two images is 30:1. The 30 to 1 resolution difference application is for the fusion of THEMIS (100 m resolution) and TES (3 km resolution) images for NASA’s Mars exploration. A paper was presented in 2017 IGARSS [19]. The performance of HCM was also excellent for this application. See Figure 4 and Table 1 in [19] for details. Those results clearly demonstrated that HCM can still perform well in 30:1 resolution difference application). Table 1 in [19] indicates that HCM actually has the best performance in this application.

4.4. Necessity and Importance of Having Diverse Methods for Image Fusion

We would like to argue that no one method could perform well under all of the conditions in many remote sensing applications. For example, a recent research by our team focused on the fusion of Planet and Worldview images. In this application, the resolution of Planet images is actually uncertain because its resolution is much worse than the declared resolution of 3.125 m. There are both homogeneous and heterogeneous regions in the images. We carried out three case studies in that paper. It was observed that none of the three methods (STARFM, FSDAF, and HCM) can outperform others in all cases. This shows that it is important to have more diversity in the fusion methods. HCM is simple and efficient, and hence may be more suitable for near real-time applications. On the other hand, FSDAF and STARFM require more computational times and may be suitable for batch, off-line processing applications. The bottom line is that the remote sensing community needs to have some freedom in choosing the most appropriate fusion method that can meet each individual’s specific needs. In this respect, HCM offers a reasonable alternative.

4.5. Combine HCM with Image Clustering

We have implemented a general clustering approach, which does not require the cluster maps at different times to be the same. To perform the clustering, we use k-means for MODIS images at t_k and t_p. The clusters can be dramatically different at two different times. Let us use Figure 11 below to illustrate our idea. At t_k, there are three clusters and at t_p, there are four clusters. When we overlay the cluster maps, we will have six combinations of clusters. If there are N clusters at t_k and M clusters at t_p, then there will be at most NM clusters in total. In each cluster, we estimate a matrix F. We applied this clustering approach to two cases. The results are shown below.

4.5.1. Example in Homogeneous Area

We used Day 128 to predict Day 144. We tried three cluster combinations: 50 × 50; 20 × 20; and, 5 × 5, where the first number indicates the number of clusters at time t_k and the second number is the number of clusters at t_p. From

Table 8. Comparison of cluster based HCM with different cluster sizes and local based HCM for homogeneous areas. Bold numbers indicate high performing methods.

Cluster 50 × 50	Cluster based HCM		Local based HCM
	RMSE	CC	RMSE	CC
NIR	0.0111	0.9573	0.0100	0.9699
Red	0.0060	0.9348	0.0060	0.9475
Green	0.0050	0.8999	0.0060	0.9114
Cluster 20 × 20	Cluster based HCM		Local based HCM
	RMSE	CC	RMSE	CC
NIR	0.0110	0.9580	0.0100	0.9699
Red	0.0059	0.9353	0.0060	0.9475
Green	0.0050	0.9023	0.0060	0.9114
Cluster 5 × 5	Cluster based HCM		Local based HCM
	RMSE	CC	RMSE	CC
NIR	0.0105	0.9615	0.0100	0.9699
Red	0.0059	0.9372	0.0060	0.9475
Green	0.0048	0.9086	0.0060	0.9114

, it can be seen that the local HCM approach is slightly better than the cluster based approach.

4.5.2. Example in Heterogeneous Area

We used Day 214 to predict Day 246. We tried three cluster combinations: 50 × 50; 20 × 20; and, 5 × 5. Again, from

Table 9. Comparison of cluster based HCM with different cluster sizes and local based HCM for heterogeneous areas. Bold numbers indicate high performing methods.

Chister 50 × 50	Chister based HCM		Local based HCM
	RMSE	CC	RMSE	CC
NIR	0.0359	0.8695	0.0353	0.8700
Red	0.0171	0.7948	0.0167	0.7977
Green	0.0124	0.7857	0.0126	0.7876
Bhie	0.0082	0.8724	0.0070	0.8804
SW1	0.0171	0.8789	0.0170	0.8793
SW2	0.0178	0.8444	0.0175	0.8456
Chister 20 × 20	Chister based HCM		Local based HCM
	RMSE	CC	RMSE	CC
NIR	0.0360	0.8687	0.0353	0.8700
Red	0.0170	0.7959	0.0167	0.7977
Green	0.0124	0.7858	0.0126	0.7876
Bhie	0.0081	0.8729	0.0070	0.8804
SW1	0.0171	0.8785	0.0170	0.8793
SW2	0.0178	0.8443	0.0175	0.8456
Chister 5 × 5	Chister based HCM		Local based HCM
	RMSE	CC	RMSE	CC
NIR	0.0369	0.8603	0.0353	0.8700
Red	0.0173	0.7885	0.0167	0.7977
Green	0.0125	0.7791	0.0126	0.7876
Bhie	0.0080	0.8725	0.0070	0.8804
SW1	0.0173	0.8757	0.0170	0.8793
SW2	0.0179	0.8403	0.0175	0.8456

, it can be seen that the two approaches have very close performances and the local based method has a very slight edge over the cluster based approach.

When comparing the cluster-based HCM with non-cluster/local based HCM, we see that the results are mixed. We do see some cases where the cluster-based approach is slightly better, but in other cases, the non-cluster based HCM performs well. A simple explanation is that our non-cluster based HCM is local in nature. Since we normally set the patch size to be small for heterogeneous areas, the pixels within those small patches generally do not have much variation.

We would also like to mention that there is another clustering based method (STI-FM) [10]. The idea is to use the ratio of MODIS pixels at two different times to perform clustering. We implemented that algorithm and included the results in this paper. See Table 2, Table 3, Table 4, Table 5 and Table 6 in Section 3.

In short, the use of clustering based approach could be a good future research direction, especially in the case of heterogeneous images.

4.6. General Comments and Observations

For homogeneous regions, our proposed HCM algorithm performed the best in terms of objective evaluations using seven performance metrics. See Table 2, Table 3 and Table 4 for details. Those seven performance metrics are widely used in the literature to compare image fusion and pansharpening algorithms.

In terms of subjective visualization for homogeneous regions, one can see that our results are comparable or better than others. Some details in Figure 4, Figure 5 and Figure 6 clearly show more closeness to the ground truth by using the proposed method.

For heterogeneous regions, the proposed HCM method is slightly inferior to that of FSDAF, which explicitly incorporates land cover classification. However, in some bands, such as SW1 and SW2, our results are comparable or better than that of FSDAF in terms of objective metrics. In terms of subjective comparisons, our prediction performance is comparable to that of the other methods.

In terms of computational complexity, STARFM completes the prediction of one image in less than 3 min, while FSDAF completes the prediction of one image in about 1.5 h for both datasets. There is a fast variant of FSDAF in that package. However, the prediction performance is not as good as the slow version. STI-FM completes a forward prediction in about 2 s for both of the datasets. The computational time for HCM is comparable to that of STI-FM, but varies depending on which dataset is used since different parameters were used for each dataset. For the homogenous dataset, the computational time for a single prediction is roughly 10 s, while for the heterogeneous dataset, the computational time is about 8 min.

Since none of the prediction methods can work well under all situations, it might be better to adopt a hybrid approach for Landsat and MODIS image fusion. That is, we propose to use HCM for homogeneous areas and FSDAF or STI-FM for heterogeneous areas.

One future research is to incorporate the high temporal resolution fused images into a remote sensing data product, such as fire damage assessment. Another potential research direction is to apply deep learning approach to learn the mapping between the MODIS images and then use that mapping for Landsat image prediction. A third direction is to utilize the high temporal and high spatial resolution images for anomaly detection, border monitoring, and target detection.

5. Conclusions

In this paper, we present a simple, and high performance forward prediction approach to generating Landsat images with high temporal resolution. The idea is based on learning a mapping between MODIS images. Once the mapping is learned, it is then applied to a Landsat image that is collected at an earlier time in order to predict a future Landsat image. When compared to other fusion approaches, such as STAARCH and ESTARFM, our approach does not require two pairs of MODIS and Landsat images, and hence it is more appropriate for forward prediction. Experiments using actual MODIS and Landsat images demonstrated that the proposed approach achieves a comparable performance as that of STARFM, STI-FM, and FSDAF. The comparisons were done at least after the three digits of the decimal point. Consequently, the outcomes were similar in comparison to the other methods. In addition, computationally, the proposed HCM and STI-FM were found to be relatively simpler in comparison to the other two methods.