Estimation of Surface Duct Using Ground-Based GPS Phase Delay and Propagation Loss
Abstract
:1. Introduction
2. Forward Model
2.1. Phase-Delay Model
2.2. Propagation-Loss Model
3. Improved Inversion Algorithm
3.1. Proposed NSSAGA Algorithm
3.2. Implementation Steps
3.3. Modeling Refractivity Profile and Objective Function
4. Results
4.1. Comparison between NSSAGA and NSGA-II
4.2. NSSAGA with Different Levels of Gaussian Noise
4.3. Analysis of Retrieved Propagation Loss
4.4. NSSAGA with Different Objective Functions
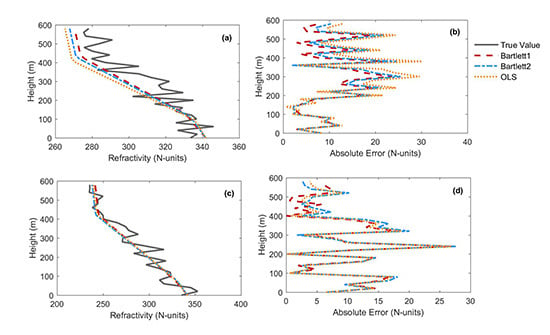
4.5. Experimental Data Testing
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Wang, B.; Wu, Z.S.; Zhao, Z.W.; Wang, H.G. A Passive Technique to Monitor Evaporation Duct Height Using Coastal GNSS-R. IEEE Geosci. Remote Sens. 2011, 8, 587–591. [Google Scholar] [CrossRef]
- Sun, Z.; Ning, H.; Song, S.; Yan, D. First observations of elevated ducts associated with intermittent turbulence in the stable boundary layer over Bosten Lake, China. J. Geophys. Res. Atmos. 2016, 121. [Google Scholar] [CrossRef]
- Turton, J.D.; Bennetts, D.A.; Farmer, S.F.G. An introduction to radio ducting. Meteorol. Mag. 1988, 117, 245–254. [Google Scholar]
- Ding, J.; Fei, J.; Huang, X.; Cheng, X.; Hu, X. Observational Occurrence of Tropical Cyclone Ducts from GPS Dropsonde Data. J. Appl. Meteorol. Clim. 2013, 52, 1221–1236. [Google Scholar] [CrossRef]
- Thompson, W.T.; Haack, T. An Investigation of Sea Surface Temperature Influence on Microwave Refractivity: The Wallops-2000 Experiment. J. Appl. Meteorol. Clim. 2011, 50, 2319–2337. [Google Scholar] [CrossRef]
- Atkinson, B.W.; Li, J.-G.; Plant, R.S. Numerical Modeling of the Propagation Environment in the Atmospheric Boundary Layer over the Persian Gulf. J. Appl. Meteorol. 2001, 40, 586–603. [Google Scholar] [CrossRef]
- Haack, T.; Burk, S.D. Summertime Marine Refractivity Conditions along Coastal California. J. Appl. Meteorol. 2001, 40, 673–687. [Google Scholar] [CrossRef]
- Feng, Y.-C.; Fabry, F.; Weckwerth, T.M. Improving Radar Refractivity Retrieval by Considering the Change in the Refractivity Profile and the Varying Altitudes of Ground Targets. J. Atmos. Ocean. Technol. 2016, 33, 989–1004. [Google Scholar] [CrossRef]
- Wagner, M.; Gerstoft, P.; Rogers, T. Estimating refractivity from propagation loss in turbulent media. Radio Sci. 2016, 51. [Google Scholar] [CrossRef]
- Gerstoft, P.; Gingras, D.F.; Rogers, L.T.; Hodgkiss, W.S. Estimation of radio refractivity structure using matched-field array processing. IEEE Trans. Antennas Propag. 2000, 48, 345–356. [Google Scholar] [CrossRef]
- Zeng, Y.; Blahak, U.; Neuper, M.; Jerger, D. Radar Beam Tracing Methods Based on Atmospheric Refractive Index. J. Atmos. Ocean. Technol. 2014, 31, 2650–2670. [Google Scholar] [CrossRef]
- Shume, E.; Ao, C. Remote sensing of tropospheric turbulence using GPS radio occultation. Atmos. Meas. Tech. 2016, 9, 3175–3182. [Google Scholar] [CrossRef]
- Fountoulakis, V.; Earls, C. Duct heights inferred from radar sea clutter using proper orthogonal bases. Radio Sci. 2016, 51. [Google Scholar] [CrossRef]
- Hallali, R.; Dalaudier, F.; Parent du Chatelet, J. Comparison between Radar and Automatic Weather Station Refractivity Variability. Bound.-Layer Meteorol. 2016, 160, 299–317. [Google Scholar] [CrossRef]
- Krolik, J.; Tabrikian, J. Tropospheric refractivity estimation using radar clutter from the sea surface. In Proceedings of the Battlespace Atmospheric Conference, San Diego, CA, USA, 2–4 December 1997. [Google Scholar]
- Gerstoft, P.; Rogers, L.T.; Hodgkiss, W.S.; Wagner, L.J. Refractivity estimation using multiple elevation angles. IEEE J. Ocean. Eng. 2003, 28, 513–525. [Google Scholar] [CrossRef]
- Gerstoft, P.; Rogers, L.T.; Krolik, J.L.; Hodgkiss, W.S. Inversion for refractivity parameters from radar sea clutter. Radio Sci. 2003, 38. [Google Scholar] [CrossRef]
- Sheng, Z. The estimation of lower refractivity uncertainty from radar sea clutter using the Bayesian—MCMC method. Chin. Phys. B 2013, 22. [Google Scholar] [CrossRef]
- Douvenot, R.; Fabbro, V.; Gerstoft, P.; Bourlier, C.; Saillard, J. A duct mapping method using least squares support vector machines. Radio Sci. 2008, 43. [Google Scholar] [CrossRef] [Green Version]
- Yardim, C.; Gerstoft, P.; Hodgkiss, W.S. Tracking Refractivity from Clutter Using Kalman and Particle Filters. IEEE Trans. Antennas Propag. 2008, 56, 1058–1070. [Google Scholar] [CrossRef]
- Wen, D.; Yuan, Y.; Ou, J.; Zhang, K. Ionospheric Response to the Geomagnetic Storm on August 21, 2003 over China Using GNSS-Based Tomographic Technique. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3212–3217. [Google Scholar] [CrossRef]
- Sheng, Z.; Wang, J.; Zhou, S.; Zhou, B. Parameter estimation for chaotic systems using a hybrid adaptive cuckoo search with simulated annealing algorithm. Chaos 2014, 24. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Huang, S. Atmospheric Duct Estimation Using Radar Sea Clutter Returns by the Adjoint Method with Regularization Technique. J. Atmos. Ocean. Technol. 2014, 31, 1250–1262. [Google Scholar] [CrossRef]
- Karimian, A.; Yardim, C.; Gerstoft, P.; Hodgkiss, W.S.; Barrios, A.E. Refractivity estimation from sea clutter: An invited review. Radio Sci. 2011, 46. [Google Scholar] [CrossRef]
- Zhao, X.; Yardim, C.; Wang, D.; Howe, B.M. Estimating range-dependent evaporation duct height. J. Atmos. Ocean. Technol. 2017, 34, 1113–1123. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, Z.; Wang, B.; Wang, H.; Zhu, Q. Modeling low elevation GPS signal propagation in maritime atmospheric ducts. J. Atmos. Sol.-Terr. Phys. 2012, 80, 12–20. [Google Scholar] [CrossRef]
- Hitney, H.V. Remote sensing of refractivity structure by direct radio measurements at UHF. In AGARD, Remote Sensing of the Propagation Environment 6 p; (SEE N92-22790 13-46); Naval Ocean Systems Center: San Diego, CA, USA, 1992. [Google Scholar]
- Anderson, K.D. Tropospheric refractivity profiles inferred from low elevation angle measurements of Global Positioning System (GPS) signals. In Proceedings of the AGARD Conference the Sensor and Propagation Panel Symposium, Bremerhaven, Germany, 19–22 September 1994. [Google Scholar]
- Lowry, A.R.; Rocken, C.; Sokolovskiy, S.V.; Anderson, K.D. Vertical profiling of atmospheric refractivity from ground-based GPS. Radio Sci. 2002, 37. [Google Scholar] [CrossRef]
- Lin, L.K.; Zhao, Z.W.; Zhang, Y.R.; Zhu, Q.L. Tropospheric refractivity profiling based on refractivity profile model using single ground-based global positioning system. IET Radar Sonar Navig. 2011, 5, 7–11. [Google Scholar] [CrossRef]
- Zus, F.; Dick, G.; Heise, S.; Wickert, J. A forward operator and its adjoint for GPS slant total delays. Radio Sci. 2015, 50, 393–405. [Google Scholar] [CrossRef]
- Sheng, Z.; Fang, H.-X. Monitoring of ducting by using a ground-based GPS receiver. Chin. Phys. B 2013, 22. [Google Scholar] [CrossRef]
- Wu, X.; Wang, X.; Lü, D. Retrieval of vertical distribution of tropospheric refractivity through ground-based GPS observation. Adv. Atmos. Sci. 2014, 31. [Google Scholar] [CrossRef]
- Wu, Y.-Y.; Hong, Z.-J.; Guo, P.; Zheng, J. Simulation of Atmospheric Refractive Profile Retrieving from Low-Elevation Ground-Based GPS Observations. Chin. J. Geophys. 2010, 53, 639–645. [Google Scholar] [CrossRef]
- Liao, Q.; Sheng, Z.; Shi, H. Joint Inversion of Atmospheric Refractivity Profile Based on Ground-Based GPS Phase Delay and Propagation Loss. Atmosphere 2016, 7, 12. [Google Scholar] [CrossRef]
- Gingras, D.F.; Gerstoft, P.; Gerr, N.L. Electromagnetic matched-field processing: Basic concepts and tropospheric simulations. IEEE Trans. Antennas Propag. 1997, 45, 1536–1545. [Google Scholar] [CrossRef]
- Smith, E.K.; Weintraub, S. The Constants in the Equation for Atmospheric Refractive Index at Radio Frequencies. Proc. IRE 1953, 41, 1035–1037. [Google Scholar] [CrossRef]
- Zhao, X.; Huang, S.; Xiang, J.; Shi, W.L. Remote sensing of atmospheric duct parameters using simulated annealing. Chin. Phys. B 2011, 9. [Google Scholar] [CrossRef]
- Almond, T.; Clarke, J. Considerations of the usefulness of the microwave prediction methods on air-to-ground paths. IEEE Proc. Part F 1973, 130, 649–656. [Google Scholar] [CrossRef]
- Levy, M.F. Horizontal parabolic equation solution of radiowave propagation problems on large domains. IEEE Trans. Antennas Propag. 1995, 43, 137–144. [Google Scholar] [CrossRef]
- Teti, J. Parabolic equation methods for electromagnetic wave propagation [Book Review]. IEEE Antennnas Propag. Mag. 2001, 43, 96–97. [Google Scholar] [CrossRef]
- Balvedi, G.C.; Walter, F. Analysis of GPS signal propagation in tropospheric ducts using numerical methods. In Proceedings of the 11th URSI Commission Open Symposium on Radio Wave Propagation and Remote Sensing, Rio De Janeiro, Brazil, 30 October–2 November 2007. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q. Multiobjective Optimization Problems with Complicated Pareto Sets, MOEA/D and NSGA-II. IEEE Trans. Evolut. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Multiobjective function optimization using nondominated sorting genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Xiang, Y.; Gubian, S.; Suomela, B.; Hoeng, J. Generalized simulated annealing for global optimization: The GenSA Package. R J. 2013, 5, 13–29. [Google Scholar]
- Rogers, L.T. Likelihood estimation of tropospheric duct parameters from horizontal propagation measurements. Radio Sci. 1997, 32, 79–92. [Google Scholar] [CrossRef]
- Zus, F.; Bender, M.; Deng, Z.; Dick, G.; Heise, S.; Shang-Guan, M.; Wickert, J. A methodology to compute GPS slant total delays in a numerical weather model. Radio Sci. 2012, 47. [Google Scholar] [CrossRef] [Green Version]
- Kačmařík, M.; Douša, J.; Dick, G.; Zus, F.; Brenot, H.; Möller, G.; Pottiaux, E.; Kapłon, J.; Hordyniec, P.; Václavovic, P.; et al. Inter-technique validation of tropospheric slant total delays. Atmos. Meas. Tech. 2017, 10, 2183–2208. [Google Scholar] [CrossRef]













| Parameters | Inversion Slope c1 | Height h1 | Inversion Slope c2 | Height h2 | |
|---|---|---|---|---|---|
| Units | N-units/m | m | N-units/m | m | |
| Lower bound | −0.1 | 50 | −0.4 | 250 | |
| Upper bound | 0 | 150 | 0 | 350 | |
| True value | −0.02 | 100 | −0.2 | 300 | |
| NSSAGA | 20 m | −0.0302 (51%) | 107.4749 (7.5%) | −0.1979 (−1.1%) | 296.8430 (−1.1%) |
| 100 m | −0.0524 (162%) | 116.8249 (16.8%) | −0.1894 (−5.3%) | 295.6861 (−1.4%) | |
| 150 m | −0.0264 (32%) | 104.6840 (4.7%) | −0.1952 (−2.4%) | 305.6387 (1.9%) | |
| 400 m | −0.0414 (107%) | 106.5472 (6.6%) | −0.1966 (−1.7%) | 286.0859 (−4.6%) | |
| NSGA-II | 20 m | −0.0247 (23.5%) | 51.3844 (−48.6%) | −0.2103 (5.2%) | 288.6211 (−3.8%) |
| 100 m | −0.0615 (207.5%) | 83.1727 (−16.8%) | −0.2213 (10.7%) | 255.8522 (−14.7%) | |
| 150 m | −0.0767 (283.5%) | 111.1971 (11.2%) | −0.1633 (−18.4%) | 326.9079 (9.0%) | |
| 400 m | −0.0021 (−89.5%) | 77.9154 (−22.1%) | −0.2430 (21.5%) | 253.9479 (−15.4%) | |
| Antenna Height and Gaussian Noise Level | Inversion Slope c1 | Height h1 | Inversion Slope c2 | Height h2 | |
|---|---|---|---|---|---|
| 20 m | 3% | −0.0345 (72.5%) | 132.8208 (32.8%) | −0.2367 (18.4%) | 302.0072 (0.7%) |
| 5% | −0.0366 (83%) | 113.3292 (13.3%) | −0.2415 (20.8%) | 290.9717 (−3%) | |
| 7% | −0.0274 (37%) | 106.8854 (6.9%) | −0.2338 (16.9%) | 310.0565 (3.4%) | |
| 10% | −0.0504 (152%) | 127.7177 (27.7%) | −0.2816 (40.8%) | 318.0503 (6%) | |
| 50 m | 3% | −0.0419 (109.5%) | 76.6365 (−23.4%) | −0.2886 (44.3%) | 279.2205 (−6.9%) |
| 5% | −0.0650 (225%) | 63.5319 (−36.5%) | −0.3299 (65.0%) | 265.9958 (11.3%) | |
| 7% | −0.0476 (138%) | 93.6565 (−6.3%) | −0.3476 (73.8%) | 281.2179 (−6.3%) | |
| 10% | −0.0737 (268.5%) | 59.1222 (−40.9%) | −0.39 (95%) | 284.2965 (−5.2%) | |
| 100 m | 3% | −0.0597 (198.5%) | 113.8418 (13.8%) | −0.2289 (14.5%) | 302.8125 (0.9%) |
| 5% | −0.0372 (86%) | 120.9352 (20.9%) | −0.2364 (18.2%) | 299.3216 (−0.2%) | |
| 7% | −0.0565 (182.5%) | 132.5776 (32.6%) | −0.2576 (28.8%) | 311.2225 (3.7%) | |
| 10% | −0.0344 (72%) | 136.8554 (36.9%) | −0.3036 (−51.8%) | 316.0985 (5.4%) | |
| 150 m | 3% | −0.0213 (6.50%) | 120.1325 (20.1%) | −0.2355 (17.8%) | 307.1159 (2.4%) |
| 5% | −0.0402 (101%) | 102.1663 (2.2%) | −0.2540 (27%) | 295.8991 (−1.4%) | |
| 7% | −0.0337 (68.5%) | 92.4479 (−7.6%) | −0.2503 (25.2%) | 279.4482 (−6.9%) | |
| 10% | −0.0487 (143.5%) | 104.5684 (4.6%) | −0.3024 (51.2%) | 313.3066 (4.4%) | |
| 400 m | 3% | −0.0350 (75%) | 106.1164 (6.1%) | −0.2218 (11.0%) | 315.5805 (5.2%) |
| 5% | −0.0476 (138%) | 91.6220 (−8.4%) | −0.2701 (35.1%) | 286.7822 (−4.4%) | |
| 7% | −0.03 (50%) | 90.6699 (−9.3%) | −0.2999 (50.0%) | 293.5933 (−2.1%) | |
| 10% | −0.0774 (287%) | 126.2492 (26.3%) | −0.2969 (48.5%) | 298.8726 (−0.4%) | |
| Objective Function | Inversion Slope c1 | Height h1 | Inversion Slope c2 | Height h2 | |
|---|---|---|---|---|---|
| NSSAGA | Bartlett1 | −0.0306 (53%) | 104.3187 (4.3%) | −0.2024 (1.2%) | 289.7689 (−3.4%) |
| Bartlett2 | −0.0505 (152.5%) | 124.6875 (24.7%) | −0.1998 (−0.1%) | 279.5246 (−6.8%) | |
| OLS | −0.0158 (−21%) | 101.5392 (1.5%) | −0.2018 (0.9%) | 301.2038 (0.4%) | |
| 20 m | −0.0302 (51%) | 107.4749 (7.5%) | −0.1979 (−1.1%) | 296.8430 (−1.1%) | |
| 150 m | −0.0264 (32%) | 104.6840 (4.7%) | −0.1952 (−2.4%) | 305.6387 (1.9%) | |
| Objective Function and Noise Level | Inversion Slope c1 | Height h1 | Inversion Slope c2 | Height h2 | |
|---|---|---|---|---|---|
| Bartlett1 | 3% | −0.0476 (138%) | 125.2315 (25.2%) | −0.2287 (14.4%) | 306.4400 (2.2%) |
| 5% | −0.0578 (189%) | 132.5299 (32.5%) | −0.2484 (24.2%) | 312.4563 (4.2%) | |
| 7% | −0.0557 (178.5%) | 117.3913 (17.4%) | −0.2791 (39.6%) | 321.0724 (7.0%) | |
| 10% | −0.0572 (186%) | 125.0450 (25.1%) | −0.2768 (38.4%) | 339.8595 (13.3%) | |
| Bartlett2 | 3% | −0.0461 (130.5%) | 119.1744 (19.2%) | −0.2043 (2.2%) | 311.4039 (3.8%) |
| 5% | −0.0497 (148.5%) | 123.1673 (23.2%) | −0.2330 (16.5%) | 308.2942 (2.8%) | |
| 7% | −0.0453 (126.5%) | 138.2198 (38.2%) | −0.2799 (40.0%) | 308.1836 (2.7%) | |
| 10% | −0.0470 (135%) | 109.1366 (9.1%) | −0.2911 (45.6%) | 327.2096 (9.1%) | |
| OLS | 3% | −0.0408 (104%) | 123.0645 (23.1%) | −0.2418 (20.9%) | 304.0172 (1.3%) |
| 5% | −0.0599 (199.5%) | 140.5727 (40.6%) | −0.2423 (21.2%) | 329.4880 (9.8%) | |
| 7% | −0.0498 (149%) | 111.2574 (11.3%) | −0.2934 (46.7%) | 304.5782 (1.5%) | |
| 10% | −0.0523 (161.5%) | 125.7983 (25.8%) | −0.3477 (73.9%) | 312.7544 (4.3%) | |
| Parameters | Inversion Slope c1 (N-Units/m) | Height h1 (m) | Inversion Slope c2 (N-Units/m) | Height h2 (m) | RMS Error (N) | |
|---|---|---|---|---|---|---|
| Case1 | Bartlett1 | −0.0746 | 110.9846 | −0.1960 | 317.8961 | 11.4734 |
| Bartlett2 | −0.0867 | 127.4610 | −0.1875 | 303.5692 | 12.6298 | |
| OLS | −0.0627 | 94.7159 | −0.2120 | 314.6175 | 14.3666 | |
| Case2 | Bartlett1 | −0.1689 | 77.0123 | −0.2138 | 341.3519 | 8.9907 |
| Bartlett2 | −0.1477 | 76.1761 | −0.2549 | 351.2348 | 9.0134 | |
| OLS | −0.1619 | 87.1056 | −0.2513 | 342.0737 | 9.2483 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Q.; Sheng, Z.; Shi, H.; Xiang, J.; Yu, H. Estimation of Surface Duct Using Ground-Based GPS Phase Delay and Propagation Loss. Remote Sens. 2018, 10, 724. https://doi.org/10.3390/rs10050724
Liao Q, Sheng Z, Shi H, Xiang J, Yu H. Estimation of Surface Duct Using Ground-Based GPS Phase Delay and Propagation Loss. Remote Sensing. 2018; 10(5):724. https://doi.org/10.3390/rs10050724
Chicago/Turabian StyleLiao, Qixiang, Zheng Sheng, Hanqing Shi, Jie Xiang, and Hong Yu. 2018. "Estimation of Surface Duct Using Ground-Based GPS Phase Delay and Propagation Loss" Remote Sensing 10, no. 5: 724. https://doi.org/10.3390/rs10050724
APA StyleLiao, Q., Sheng, Z., Shi, H., Xiang, J., & Yu, H. (2018). Estimation of Surface Duct Using Ground-Based GPS Phase Delay and Propagation Loss. Remote Sensing, 10(5), 724. https://doi.org/10.3390/rs10050724