Geostationary Sensor Based Forest Fire Detection and Monitoring: An Improved Version of the SFIDE Algorithm
Abstract
:1. Introduction
2. Data and Methodology
2.1. Data & Methods
- Fire events reported by CFVA (Corpo Forestale e di Vigilanza Ambientale) of the Sardinia Region, that is the agency involved in the fire-fighting;
- Hot spots detected by the MODIS and VIIRS satellite sensors.
2.2. The SFIDE Algorithm
- Preliminary operations and applications of masks;
- Fixed thresholds;
- Potential hot-spot detection;
- Hot-spot confirmation;
- Hot-spot characterization.
2.2.1. Preliminary Operations
2.2.2. Fixed Thresholds
2.2.3. Potential Hot-Spot Detection
2.2.4. Hot-Spot Confirmation
- Tb3.9_15’ and ΔT15’: Tb3.9 and ΔT values for image that precedes by 15 min the current one;
- Tb3.9_30’ and ΔT30’: Tb3.9 and ΔT values for image that precedes by 30 min the current one;
- ΔTb3.9_15’ = (Tb3.9 − Tb3.9_15’) and Δ(ΔT)15’ = (ΔT − ΔT15’): Tb3.9 and ΔT variations between current image and the one that precedes at 15 min;
- ΔTb3.9_30’ = (Tb3.9 − Tb3.9_30’) and Δ(ΔT)30’ = (ΔT − ΔT30’): Tb3.9 and ΔT variations between current image and the one that precedes at 30 min.
2.2.5. Contextual Analysis
2.2.6. Hot-Spot Characterization: FRP and LST
2.2.7. Nightly Hours Algorithm
- Cloud-mask identified using a threshold on channel 10;
- Hot-spot detection with fixed thresholds occurs with limit values of Tb3.9 and ΔT, adapted to nocturnal hours;
- Fixed values of Tb3.9 and ΔT as hot-spot detection thresholds;
- Contextual analysis carried out by using average value of Tb3.9 and ΔT on the whole of Sardinia;
- No distinction between high and low probability fire pixels.
3. Data Validation
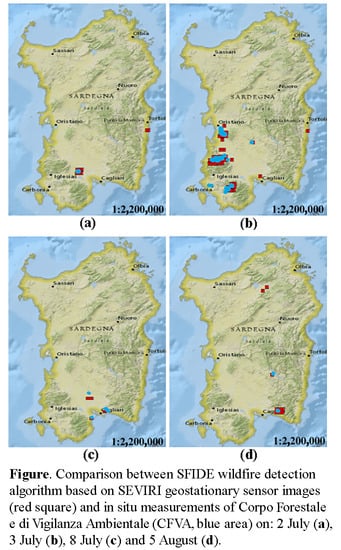
3.1. Comparison with In Situ Measurements
3.2. Comparison with MODIS Sensor
- −
- the importance of a geostationary orbit sensor that allows real time monitoring due to a high update frequency: 96 daily images by SEVIRI and 2–4 by MODIS;
- −
- that, particularly relevant, fires larger than 100 [ha] have not been detected by MODIS sensor, and this result confirms the major advantages of SFIDE algorithm also regarding the number of detected fires.
3.3. Fire Monitoring Examples
4. Conclusions
- −
- Improve the estimate of the reference temperature used to define a pixel as interested by a fire;
- −
- Improve the cloud mask accuracy thus reducing the risk of false alarms;
- −
- Exploit better the high refresh rate of the images to implement several tests for accurate detection of forest fires.
Author Contributions
Conflicts of Interest
References
- Schmuck, G.; San-Miguel-Ayanz, J.; Camia, A.; Durrant, T.; Santos De Oliveira, S.; Boca, R.; Whitmore, C.; Giovando, C.; Libertà, G.; Corti, P.; et al. Forest Fires in Europe; Publications Office of the European Union: Luxembourg, 2010. [Google Scholar]
- Laneve, G.; Fusilli, L.; Marzialetti, P.; De Bonis, R.; Bernini, G.; Tampellini, L. Development and Validation of Fire Damage-Severity Indices in the Framework of the PREFER Project. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2806–2817. [Google Scholar] [CrossRef]
- Ager, A.A.; Preisler, H.K.; Arca, B.; Spano, D.; Salis, M. Wildfire risk estimation in the Mediterranean area. Environmetrics 2009, 25, 384–396. [Google Scholar] [CrossRef]
- Sifakis, N.I.; Iossifidis, C.; Kontoes, C.; Keramitsoglou, I. Wildfire Detection and Tracking over Greece Using MSG-SEVIRI Satellite Data. Remote Sens. 2011, 3, 524–538. [Google Scholar] [CrossRef]
- Martín, M.P.; Ceccato, P.; Flasse, S.; Downey, I. Fire detection and fire growth monitoring using satellite data. In Remote Sensing of Large Wildfires; Springer: Berlin/Heidelberg, Germany, 1999; pp. 101–122. [Google Scholar]
- Dozier, J. A method for satellite identification of surface temperature fields of subpixel resolution. Remote Sens. Environ. 1981, 11, 221–229. [Google Scholar] [CrossRef]
- Salomonson, V.V.; Barnes, W.L.; Maymon, P.W.; Montgomery, H.E.; Ostrow, H. MODIS: Advanced facility instrument for studies of the earth as a system. IEEE Trans. Geosci. Remote Sens. 1989, 27, 145–153. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Justice, C.O.; Flynn, L.P.; Kendall, J.D.; Prins, E.M.; Giglio, L.; Ward, D.E.; Menzel, W.P.; Setzer, A.W. Potential global fire monitoring from EOS-MODIS. J. Geophys. Res. Atmos. 1998, 103, 32215–32238. [Google Scholar] [CrossRef]
- Justice, C.O.; Giglio, L.; Korontzi, S.; Owens, J.; Morisette, J.T.; Roy, D.; Descloitres, J.; Alleaume, S.; Petitcolin, F.; Kaufman, Y. The MODIS fire products. Remote Sens. Environ. 2002, 83, 244–262. [Google Scholar] [CrossRef]
- Giglio, L.; Descloitres, J.; Justice, C.O.; Kaufman, Y.J. An enhanced contextual fire detection algorithm for MODIS. Remote Sens. Environ. 2003, 87, 273–282. [Google Scholar] [CrossRef]
- Giglio, L.; Csiszar, I.; Restas, A.; Morisette, J.T.; Schroeder, W.; Morton, D.; Justice, C.O. Active fire detection and characterization with the advanced spaceborne thermal emission and reflection radiometer (ASTER). Remote Sens. Environ. 2008, 112, 3055–3063. [Google Scholar] [CrossRef]
- Giglio, L.; Schroeder, W.; Justice, C.O. The collection 6 MODIS active fire detection algorithm and fire products. Remote Sens. Environ. 2016, 178, 31–41. [Google Scholar] [CrossRef]
- Robinson, J.M. Fire from space: Global fire evaluation using infrared remote sensing. Int. J. Remote Sens. 1991, 12, 3–24. [Google Scholar] [CrossRef]
- Flasse, S.P.; Ceccato, P. A contextual algorithm for AVHRR fire detection. Int. J. Remote Sens. 1996, 17, 419–424. [Google Scholar] [CrossRef]
- Giglio, L.; Kendall, J.D.; Justice, C.O. Evaluation of global fire detection algorithms using simulated AVHRR infrared data. Int. J. Remote Sens. 1999, 20, 1947–1985. [Google Scholar] [CrossRef]
- Schroeder, W.; Oliva, P.; Giglio, L.; Csiszar, I.A. The new VIIRS 375 m active fire detection data product: Algorithm description and initial assessment. Remote Sens. Environ. 2014, 143, 85–96. [Google Scholar] [CrossRef]
- Prins, E.M.; Feltz, J.M.; Menzel, W.P.; Ward, D.E. An overview of GOES-8 diurnal fire and smoke results for SCAR-B and 1995 fire season in South America. J. Geophys. Res. Atmos. 1998, 103, 31821–31835. [Google Scholar] [CrossRef]
- Reid, J.S.; Koppmann, R.; Eck, T.F.; Eleuterio, D.P. A review of biomass burning emissions part II: Intensive physical properties of biomass burning particles. Atmos. Chem. Phys. 2005, 5, 799–825. [Google Scholar] [CrossRef]
- Xu, W.; Wooster, M.J.; Roberts, G.; Freeborn, P. New GOES imager algorithms for cloud and active fire detection and fire radiative power assessment across North South and Central America. Remote Sens. Environ. 2010, 114, 1876–1895. [Google Scholar] [CrossRef]
- Aminou, D.M.A. MSG’s SEVIRI instrument. ESA Bull. 2002, 111, 15–17. [Google Scholar]
- Calle, A.; Casanova, J.L.; Romo, A. Fire detection and monitoring using MSG Spinning Enhanced Visible and Infrared Imager (SEVIRI) data. J. Geophys. Res. Biogeosci. 2006, 111, G04S06. [Google Scholar] [CrossRef]
- Laneve, G.; Castronuovo, M.M.; Cadau, E.G. Continuous monitoring of forest fires in the Mediterranean area using MSG. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2761–2768. [Google Scholar] [CrossRef]
- Roberts, G.J.; Wooster, M.J. Fire detection and fire characterization over Africa using Meteosat SEVIRI. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1200–1218. [Google Scholar] [CrossRef]
- Amraoui, M.; DaCamara, C.C.; Pereira, J.M.C. Detection and monitoring of African vegetation fires using MSG-SEVIRI imagery. Remote Sens. Environ. 2010, 114, 1038–1052. [Google Scholar] [CrossRef]
- Laneve, G.; Jahjah, M.; Ferrucci, F.; Battazza, F. SIGRI project: The development of the fire vulnerability index. In Proceedings of the 34th International Symposium on Remote Sensing of Environment, Sydney, Australia, 10–15 April 2011. [Google Scholar]
- Laneve, G.; Cadau, E.; Ferrucci, F.; Rongo, R.; Guarino, A.; Fortunato, G.; Loizzo, R. SIGRI-an Integrated System for Detecting, Monitoring, Characterizing Forest Fires and Assessing damage by LEO-GEO Data. Ital. J. Remote Sens. 2012, 44, 19–25. [Google Scholar] [CrossRef]
- Laneve, G.; Jahjah, M.; Ferrucci, F.; Hirn, B.; Battazza, F.; Fusilli, L.; De Bonis, R. SIGRI project: Products validation results. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 895–905. [Google Scholar] [CrossRef]
- Schmid, J. The SEVIRI instrument. In Proceedings of the 2000 EUMETSAT Meteorological Satellite Data User’s Conference, Bologna, Italy, 29 May–2 June 2000; Volume 29. [Google Scholar]
- Saunders, R.W.; Kriebel, K.T. An improved method for detecting clear sky and cloudy radiances from AVHRR data. Int. J. Remote Sens. 1988, 9, 123–150. [Google Scholar] [CrossRef]
- Zhukov, B.; Lorenz, E.; Oertel, D.; Wooster, M.; Roberts, G. Spaceborne detection and characterization of fires during the bi-spectral infrared detection (BIRD) experimental small satellite mission (2001–2004). Remote Sens. Environ. 2006, 100, 29–51. [Google Scholar] [CrossRef]
- Wooster, M.J.; Roberts, G.; Perry, G.L.W.; Kaufman, Y.J. Retrieval of biomass combustion rates and totals from fire radiative power observations: FRP derivation and calibration relationships between biomass consumption and fire radiative energy release. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Kaiser, J.W.; Heil, A.; Andreae, M.O.; Benedetti, A.; Chubarova, N.; Jones, L.; Morcrette, J.J.; Razinger, M.; Schultz, M.G.; Suttie, M.; et al. Biomass burning emissions estimated with a global fire assimilation system based on observed fire radiative power. Biogeosciences 2012, 9, 527–554. [Google Scholar] [CrossRef] [Green Version]
- Sobrino, J.A.; Romaguera, M. Land surface temperature retrieval from MSG1-SEVIRI data. Remote Sens. Environ. 2004, 92, 247–254. [Google Scholar] [CrossRef]
- Joro, S.; Samain, O.; Yildirim, A.; Van De Berg, L.; Lutz, H.J. Towards an Improved Active Fire Monitoring Product for MSG Satellites. EUMETSAT. 2008. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.611.1456&rep=rep1&type=pdf (accessed on 9 May 2018).
- Giglio, L.; Schroeder, W. A global feasibility assessment of the bi-spectral fire temperature and area retrieval using MODIS data. Remote Sens. Environ. 2014, 152, 166–173. [Google Scholar] [CrossRef]
- Wooster, M.J.; Roberts, G.; Perry, G.L.W.; Kaufman, Y.J. Retrieval of biomass combustion rates and totals from fire radiative power observations: Application to southern Africa using geostationary SEVIRI imagery. J. Geophys. Res. 2005, 110, D21111. [Google Scholar]
- Laneve, G.; Castronuovo, M.; Cadau, E. Assessment of the fire detection limit using SEVIRI/MSG sensor. In Proceedings of the IGARSS, Denver, CO, USA, 31 July–4 August 2006; pp. 4157–4160. [Google Scholar]









| Channel | Spectral Band | Wavelength (μm) | Central Wavelength (μm) | Equator Resolution (km) |
|---|---|---|---|---|
| 1 | VIS 0.6 | 0.56–0.71 | 0.635 | 3 |
| 2 | VIS 0.8 | 0.74–0.88 | 0.81 | 3 |
| 3 | IR 1.6 | 1.50–1.78 | 1.64 | 3 |
| 4 | IR 3.9 | 3.48–4.36 | 3.92 | 3 |
| 5 | WV 6.2 | 5.35–7.15 | 6.25 | 3 |
| 6 | WV 7.3 | 6.85–7.85 | 7.35 | 3 |
| 7 | IR 8.7 | 8.30–9.10 | 8.70 | 3 |
| 8 | IR 9.7 | 9.38–9.94 | 9.66 | 3 |
| 9 | IR 10.8 | 9.80–11.80 | 10.80 | 3 |
| 10 | IR 12.0 | 11.00–13.00 | 12.00 | 3 |
| 11 | IR 13.4 | 12.40–14.40 | 13.40 | 3 |
| 12 | HRV | 0.60–0.90 | 0.75 | 1 |
| Detected Fire Events | Omitted Fire Events | Detected Hot-Spot | False Alarms |
|---|---|---|---|
| 45 | 4 (8.9%) | 464 | 32 (6.9%) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Biase, V.; Laneve, G. Geostationary Sensor Based Forest Fire Detection and Monitoring: An Improved Version of the SFIDE Algorithm. Remote Sens. 2018, 10, 741. https://doi.org/10.3390/rs10050741
Di Biase V, Laneve G. Geostationary Sensor Based Forest Fire Detection and Monitoring: An Improved Version of the SFIDE Algorithm. Remote Sensing. 2018; 10(5):741. https://doi.org/10.3390/rs10050741
Chicago/Turabian StyleDi Biase, Valeria, and Giovanni Laneve. 2018. "Geostationary Sensor Based Forest Fire Detection and Monitoring: An Improved Version of the SFIDE Algorithm" Remote Sensing 10, no. 5: 741. https://doi.org/10.3390/rs10050741
APA StyleDi Biase, V., & Laneve, G. (2018). Geostationary Sensor Based Forest Fire Detection and Monitoring: An Improved Version of the SFIDE Algorithm. Remote Sensing, 10(5), 741. https://doi.org/10.3390/rs10050741