Dynamic Monitoring and Vibration Analysis of Ancient Bridges by Ground-Based Microwave Interferometry and the ESMD Method
Abstract
:1. Introduction
2. Study Ancient Bridge and Data Acquisition
2.1. Zhaozhou Bridge
2.2. Ground-Based Microwave Interferometry
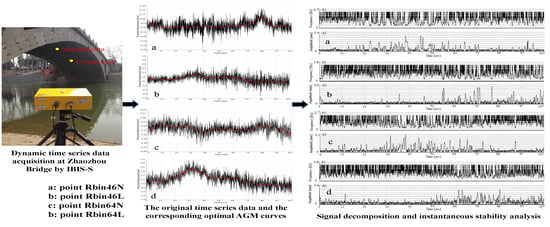
2.3. Dynamic Time Series Displacements Acquisition
3. Methods
3.1. Decomposition Algorithm of the ESMD Method for Time Series Displacements
3.2. Direct Interpolation Algorithm for Instantaneous Frequency
- Step 1:
- Traverse to find all of the quasi-extreme points of each IMF which satisfies (3), and enumerate them as set
- Step 2:
- Define the frequency interpolation coordinates by using set .
- 1:
- for 1 to m
- 2:
- if == then
- 3:
- if i == 1 then
- 4:
- ,
- 5:
- else if i == m − 1 then
- 6:
- ,
- 7:
- else
- 8:
- , , ,
- 9:
- end if
- 10:
- if and are extreme points then
- 11:
- ,
- 12:
- else
- 13:
- ,
- 14:
- ,
- 15:
- end if
- 16:
- else
- 17:
- ,
- 18:
- end if
- 19:
- end for
- Step 3:
- Add the boundary points with a linear interpolating method.
- for the left boundary point:
- if then
- ,
- else
- ,
- if then
- ,
- end if
- end if
- for the right boundary point:
- if then
- ,
- else
- ,
- if then
- ,
- end if
- end if
- Step 4:
- Obtain a curve by using cubic spline interpolation with all the discrete points .
3.3. Procedure for the Instantaneous Vibration Analysis
- (1)
- Apply the ESMD method to the dynamic time series displacements (projected displacement). Determine the optimal variance ratio with the corresponding sifting time to obtain the optimal AGM curve for each set of time series displacements, and yield a series of IMFs.
- (2)
- Compare the displacements and sudden variations of the main IMFs between the 1/4 span point and the mid-span point under the environmental excitation factors, and evaluate the instantaneous dynamic response of the 1/4 span point and the mid-span point under the environmental excitation factors.
- (3)
- Apply the direct interpolation algorithm to each IMF of the time series displacements to obtain the corresponding instantaneous frequency and amplitude, and perform the instantaneous vibration analysis of Zhaozhou Bridge by analyzing the instantaneous frequencies and amplitudes of the main IMFs related to Zhaozhou Bridge.
4. Results and Analyses
4.1. Simulation Experiment
4.2. Results of Time Series Displacements from Ground-Based Microwave Interferometry
4.3. Results of IMF Decomposition and Analysis
4.4. Results of Time-Frequency Analysis
5. Discussion
- (1)
- By adopting IBIS-S to obtain the time series displacements of Zhanzhou Bridge, ground-based microwave interferometry has been validated as an effective non-contact technique to monitor ancient bridges. Without passive radar reflectors installed on the surface of ancient bridges, the thermal SNR values of all of the monitoring points were larger than 35 dB, which could ensure that accurate displacements were obtained. Therefore, for the purpose of avoiding any damages on Zhaozhou Bridge, the traditional transducers were not attached on the bridge to evaluate the accuracy of ground-based microwave interferometry. However, as ground-based microwave interferometry makes use of the propagation of electromagnetic waves for displacement measurement, the measurements performed are inevitably influenced by the atmospheric refractive index, which is caused by temperature, humidity, air pressure, and other meteorological factors [38]. Different meteorological conditions have different atmospheric refractive index values, which can cause some loss of measurement accuracy. Therefore, if there is a need for the periodic monitoring of bridges in different measuring times using ground-based microwave interferometry, it is necessary to improve the measurement accuracy of the dynamic deflection of bridges by the use of atmospheric parameters correction, such as the Permanent Scatterers technique [38,39,40] and model-based approach [10,41]. This can improve the contrast of different period data. However, in this study, the acquisition time of all data only lasts about 30 min, and has almost the same influence of meteorological factors for displacement measurement. Moreover, the purpose of this paper is to perform the instantaneous vibration analysis of ancient bridges. Hence, it is not necessary to compensate for the propagation losses in this study, which will not affect the reliability of the instantaneous vibration analysis of ancient bridges.
- (2)
- Generally, any one complicated signal can be regarded as being composed of multiple simple signals which represent different physical meanings [32]. In this study, through the use of the ESMD method, the acquired time series displacements was decomposed into eight IMFs together with an optimal AGM curve, which are more accurate compared with the decomposed 12 IMFs by the HHT-EMD method. Furthermore, by analyzing the decomposed IMFs, the overall vibration trend and sudden variations of the projected displacement can be obtained to analyze the structural characteristics of ancient bridges. However, it is difficult to obtain the physical meaning of each IMF, which needs to be further studied. Moreover, the thrust of wind, ground-motion, complicated traffic, etc., will inevitably generate a noise signal that reduces the accuracy of the measured dynamic displacement of the bridge. In addition, the monitored bridge itself also has a periodic vibration, of which the vibration frequency is different from the transient vibration by the instant loading of a car. Therefore, the obtained dynamic displacement of the bridge, caused by the instant loading of a car, should become bigger or smaller. To the authors’ best knowledge, there is not a theoretical model or a gold standard method to determine the expected dynamic displacement in the bridge caused by the instant loading of a car. Further study of the denoising algorithm is also needed to improve the accuracy of the expected dynamic displacement caused by the instant loading. Nevertheless, the above factors influence the expected dynamic displacement caused by the instant loading a little, which will not affect the instantaneous vibration analysis in this study.
- (3)
- Instantaneous frequency is a transient structural vibration response, which not only depends on the structural natural frequency, but is also influenced by the damping, the stiffness, and the excitation conditions [20,42]. In this study, the obtained maximum instantaneous frequency is 2.49 Hz for Mode 1 only with environmental excitation factors. However, due to the stronger excitation condition of a transient load of a car, the obtained maximum instantaneous frequency increases to 3.37 Hz for Mode 1. Therefore, by using the ESMD method, it can accurately identify the variations of instantaneous frequency by a neat value for the maximum instantaneous frequency. Furthermore, it is generally known that the structural natural frequency will be reduced if some damage occurs in a structure, which can be reflected by the sudden reduction of the instantaneous frequency of the monitored structure [43,44]. In this study, according to the direct interpolation algorithm, if some damage had occurred in Zhaozhou Bridge with the transient load of a car, the instantaneous frequencies of Mode 1 should be decreased steadily. Therefore, although the maximum instantaneous frequency changed from 2.49 Hz to 3.37 Hz for Mode 1, there was no sudden steady decrease in the curve of instantaneous frequency, which indicates that it was in an instantaneous stable state when the car passed over Zhaozhou Bridge. However, Zhaozhou Bridge has been operational for 1400 years now, so if we want to detect the significant changes for the purpose of a global stability analysis, a large period of several months may be required.
6. Conclusions
- (1)
- In this study, aiming to avoid damage to the great historical heritage for Zhaozhou Bridge, the IBIS-S instrument was only located on one side of Zhaozhou Bridge without corner reflectors attached on the lower surface of Zhaozhou Bridge. The quick and easy installation of the IBIS-S instrument can greatly improve the efficiency of data collection. Moreover, the resulting thermal SNR of all of monitoring points on the lower surface of the bridge were larger than 35 dB, which could ensure that accurate displacements were obtained. Therefore, these results verify the feasibility and accuracy of the dynamic monitoring of Zhaozhou Bridge by the sensing method of ground-based microwave interferometry in the paper, which further indicates that ground-based microwave interferometry is a viable alternative technique to acquire dynamic time series displacements for the instantaneous vibration analysis of ancient bridges. Meanwhile, it can also reduce the inherent risk involved with the placement of the traditional contact transducers.
- (2)
- The ESMD method was performed to yield a series of IMFs together with an optimal AGM curve through the use of a mode symmetric about the maxima and minima points. The decomposed IMFs can reflect the overall tendency of the projected displacement according to the magnitude of the frequency. Furthermore, they can also reflect the instantaneous dynamic response of the different monitored points.
- (3)
- The instantaneous frequencies were obtained using the direct interpolation algorithm, which can reconcile the conflict between the period and the frequency, compared with the traditional time-frequency analysis methods. The instantaneous frequencies of the decomposed IMFs of each set of time series displacements showed that Zhaozhou Bridge was in a steady state when the car passed over the bridge.
- (4)
- Compared with the use of HHT for obtaining decomposed IMFs and instantaneous frequencies, the results showed that the proposed method is a new and powerful alternative technique for the instantaneous vibration analysis of ancient bridges.
Author Contributions
Funding
Conflicts of Interest
References
- Liu, X.L.; Tong, X.H.; Yin, X.J.; Gu, X.L.; Ye, Z. Videogrammetric technique for three-dimensional structural progressive collapse measurement. Measurement 2015, 63, 87–89. [Google Scholar] [CrossRef]
- Roveri, N.; Carcaterra, A. Damage detection in structures under traveling loads by Hilbert–Huang transform. Mech. Syst. Signal Process. 2012, 28, 128–144. [Google Scholar] [CrossRef]
- Lee, J.W.; Kim, J.D.; Yun, C.B.; Yi, J.H.; Shim, J.M. Health-monitoring method for bridges under ordinary traffic loading. J. Sound Vib. 2002, 257, 247–264. [Google Scholar] [CrossRef]
- Heieh, K.M.; Halling, H.W.; Barr, P.J. Overview of vibrational structural health monitoring with representative case studies. J. Bridge Eng. 2006, 11, 707–715. [Google Scholar]
- Xu, Y.L.; Chen, B.; Ng, C.L.; Wong, K.Y.; Chan, W.Y. Monitoring temperature effect on a long suspension bridge. Struct. Control Health Monit. 2010, 17, 632–653. [Google Scholar] [CrossRef]
- Gentile, C.; Bernardini, G. An interferometric radar for non-contact measurement of deflections on civil engineering structures: Laboratory and full-scale tests. Struct. Infrastruct. Eng. 2010, 6, 521–534. [Google Scholar] [CrossRef]
- Pieraccini, M.; Fratini, M.; Parrini, F.; Atzeni, C. Dynamic monitoring of bridges using a high-speed coherent radar. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3284–3288. [Google Scholar] [CrossRef]
- Gentile, C. Application of microwave remote sensing to dynamic testing of stay-cables. Remote Sens. 2009, 2, 36–51. [Google Scholar] [CrossRef]
- Stabile, T.A.; Perrone, A.; Gallipoli, M.R.; Ditommaso, R.; Ponzo, F.C. Dynamic survey of the Musmeci bridge by joint application of ground-based microwave radar interferometry and ambient noise standard spectral ratio techniques. IEEE Geosci. Remote Sens. Lett. 2013, 10, 870–874. [Google Scholar] [CrossRef]
- Liu, X.L.; Tong, X.H.; Ding, K.L.; Zhao, X.A.; Zhu, L.; Zhang, X.D. Measurement of Long-Term Periodic and Dynamic Deflection of the Long-Span Railway Bridge Using Microwave Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4531–4538. [Google Scholar] [CrossRef]
- Negulescu, C.; Luzi, G.; Crosetto, M.; Raucoules, D.; Roullé, A.; Monfort, D.; Pujades, L.; Colas, B.; Dewez, T. Comparison of seismometer and radar measurements for the modal identification of civil engineering structures. Eng. Struct. 2013, 51, 10–22. [Google Scholar] [CrossRef]
- Pieraccini, M.; Fratini, M.; Parrini, F.; Atzeni, C.; Partoli, G. Interferometric radar vs. accelerometer for dynamic monitoring of large structures: An experimental comparison. NDT & E Int. 2008, 41, 258–264. [Google Scholar]
- Gökdağ, H.; Kopmaz, O. A new damage detection approach for beam-type structures based on the combination of continuous and discrete wavelet transforms. J. Sound Vib. 2009, 324, 1158–1180. [Google Scholar] [CrossRef]
- Khorram, A.; Bakhtiari-Nejad, F.; Rezaeian, M. Comparison studies between two wavelet based crack detection methods of a beam subjected to a moving load. Int. J. Eng. Sci. 2012, 51, 204–215. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, M.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis. Proc. R. Soc. Lond. 1998, A454, 903–995. [Google Scholar] [CrossRef]
- Wang, J.L.; Li, Z.J. Extreme-Point Symmetric Mode Decomposition Method for Data Analysis. Adv. Adapt. Data Anal. 2013, 5, 1350015. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Zhao, D. An improved EMD and its applications to find the basis functions of EMI signals. Math. Probl. Eng. 2015, 150127. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A review on Hilbert-Huang transform: Method and its applications to geophysical studies. Rev. Geophys. 2008, 46. [Google Scholar] [CrossRef]
- Quek, S.T.; Tua, P.S.; Wang, Q. Detecting anomalies in beams and plate based on the Hilbert-Huang transform of real signals. Smart Mater. Struct. 2003, 12, 447–460. [Google Scholar] [CrossRef]
- Chen, H.G.; Yan, Y.J.; Jiang, J.S. Vibration-based damage detection in composite wingbox structures by HHT. Mech. Syst. Signal Process. 2007, 21, 307–321. [Google Scholar] [CrossRef]
- Kunwar, A.; Jha, R.; Whelan, M.; Janoyan, K. Damage detection in an experimental bridge model using Hilbert–Huang transform of transient vibrations. Struct. Control Health 2013, 20, 201–215. [Google Scholar] [CrossRef]
- Yang, W.A.; Zhou, W.; Liao, W.; Guo, Y. Identification and quantification of concurrent control chart patterns using extreme-point symmetric mode decomposition and extreme learning machines. Neurocomputing 2015, 147, 260–270. [Google Scholar] [CrossRef]
- Liu, X.L.; Tang, Y.; Lu, Z.; Huang, H.; Tong, X.H.; Ma, J. ESMD-based stability analysis in the progressive collapse of a building model: A case study of a reinforced concrete frame-shear wall model. Measurement 2018, 120, 34–42. [Google Scholar] [CrossRef]
- Song, S.; Ding, M.; Li, H.; Song, X.; Fan, W.; Zhang, X.; Xu, H. Frequency specificity of fMRI in mesial temporal lobe epilepsy. PLoS ONE 2016, 11, e0157342. [Google Scholar] [CrossRef] [PubMed]
- Qian, L.X. New insight into an ancient stone arch bridge—The Zhao-Zhou Bridge of 1400 years old. Int. J. Mech. Sci. 1987, 29, 831–843. [Google Scholar] [CrossRef]
- Au, F.T.K.; Wang, J.J.; Liu, G.D. Construction control of reinforced concrete arch bridges. J. Bridge Eng. 2003, 8, 39–45. [Google Scholar] [CrossRef]
- Audenaert, A.; Peremans, H.; Reniers, G. An analytical model to determine the ultimate load on masonry arch bridges. J. Eng. Math. 2007, 59, 323–336. [Google Scholar] [CrossRef]
- Gentile, C. Deflection measurement on vibrating stay cables by non-contact microwave interferometer. NDT E Int. 2010, 43, 231–240. [Google Scholar] [CrossRef]
- Beben, D. Application of the interferometric radar for dynamic tests of corrugated steel plate (CSP) culvert. NDT E Int. 2011, 44, 405–412. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Luzi, G.; Cuevas-Gonzalez, M.; Devanthery, N. A noninterferometric procedure for deformation measurement using GB-SAR imagery. IEEE Geosci. Remote Sens. Lett. 2014, 11, 34–38. [Google Scholar] [CrossRef]
- Montuori, A.; Luzi, G.; Bignami, C.; Gaudiosi, I.; Stramondo, S.; Crosetto, M.; Buongiorno, M.F. The Interferometric Use of Radar Sensors for the Urban Monitoring of Structural Vibrations and Surface Displacements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3761–3776. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z.; Long, S.R.; Arnold, K.C.; Chen, X.; Blank, K. On instantaneous frequency. Adv. Adapt. Data Anal. 2009, 1, 177–229. [Google Scholar] [CrossRef]
- Zhang, R.R.; King, R.; Olson, L.; Xu, Y.L. Dynamic response of the Trinity River Relief Bridge to controlled pile damage: Modeling and experimental data analysis comparing Fourier and Hilbert–Huang techniques. J. Sound Vib. 2005, 285, 1049–1070. [Google Scholar] [CrossRef]
- Gonzalez, I.; Karoumi, R. Analysis of the annual variations in the dynamic behavior of a ballasted railway bridge using Hilbert transform. Eng. Struct. 2014, 60, 126–132. [Google Scholar] [CrossRef]
- Carbajo, E.S.; Carbajo, R.S.; Mc Goldrick, C.; Basu, B. ASDAH: An automated structural change detection algorithm based on the Hilbert–Huang transform. Mech. Syst. Signal Process. 2014, 47, 78–93. [Google Scholar] [CrossRef]
- Liu, X.L.; Zhao, X.A.; Ding, K.L.; Zhu, L.; Ma, J.; Dong, Y.Q.; Tong, X.H. Application of ground-based synthetic aperture radar technique for emergency monitoring of deep foundation excavation. J. Appl. Remote Sens. 2015, 9, 096021. [Google Scholar] [CrossRef]
- Rödelsperger, S. Real-Time Processing of Ground Based Synthetic apeRture Radar (GB-SAR) Measurement; Fachbereich Bauingenieurwesen und Geodäsie, Technische Universität Darmstadt: Darmstadt, Germany, 2011. [Google Scholar]
- Noferini, L.; Pieraccini, M.; Mecatti, D.; Luzi, G.; Atzeni, C.; Tamburini, A.; Broccolato, M. Permanent scatterers analysis for atmospheric correction in ground-based SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1459–1471. [Google Scholar] [CrossRef]
- Pipia, L.; Fábregas, X.; Aguasca, A.; Lopez-Martinez, C. Atmospheric artifact compensation in ground-based DInSAR applications. IEEE Geosci. Remote Sens. Lett. 2008, 5, 88–92. [Google Scholar] [CrossRef]
- Leva, D.; Nico, G.; Tarchi, D.; Fortuny-Guasch, J.; Sieber, A.J. Temporal analysis of a landslide by means of a ground-based SAR interferometer. IEEE Trans. Geosci. Remote Sens. 2003, 41, 745–752. [Google Scholar] [CrossRef]
- Iannini, L.; Guarnieri, A.M. Atmospheric Phase Screen in Ground-Based Radar: Statistics and Compensation. IEEE Geosci. Remote Sens. Lett. 2011, 8, 537–541. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. Signal processing techniques for vibration-based health monitoring of smart structures. Arch. Comput. Method Eng. 2016, 23, 1–15. [Google Scholar] [CrossRef]
- Wang, Z.C.; Xin, Y.; Ren, W.X. Nonlinear structural joint model updating based on instantaneous characteristics of dynamic responses. Mech. Syst. Signal Process. 2016, 76, 476–496. [Google Scholar] [CrossRef]
- Salawu, O.S. Detection of structural damage through changes in frequency: A review. Eng. Struct. 1997, 19, 718–723. [Google Scholar] [CrossRef]















| Parameter | Test 1 | Test 2 |
|---|---|---|
| Maximum distance | 200 m | 200 m |
| Working frequency | 16.6–16.9 GHZ | 16.6–16.9 GHZ |
| Range resolution | 0.5 m | 0.5 m |
| Sampling rate | 199.17 Hz | 199.17 Hz |
| Duration | 00:02:45 | 00:01:47 |
| Excitation condition | Environmental excitation | Transient loads |
| Point Name | Minimum Variance Ratio | Sifting Time (Number of Times) |
|---|---|---|
| Rbin46_N | 86.8% | 11 |
| Rbin46_L | 84.7% | 8 |
| Rbin64_N | 82.4% | 10 |
| Rbin64_L | 62.5% | 14 |
| Point | Parameter | F1 | F2 | F3 | F4 |
|---|---|---|---|---|---|
| Rbin46_N | MN (Hz) | 2.413 | 0.716 | 0.313 | 0.146 |
| SD (Hz) | 0.348 | 0.297 | 0.149 | 0.053 | |
| CV (%) | 14.4 | 41.5 | 47.6 | 36.3 | |
| Rbin46_Y | MN (Hz) | 3.362 | 0.901 | 0.391 | 0.207 |
| SD (Hz) | 0.582 | 0.379 | 0.184 | 0.074 | |
| CV (%) | 17.3 | 42.1 | 47.1 | 35.7 | |
| Rbin64_N | MN (Hz) | 2.422 | 0.715 | 0.314 | 0.145 |
| SD (Hz) | 0.351 | 0.296 | 0.151 | 0.053 | |
| CV (%) | 14.5 | 41.4 | 48.1 | 36.6 | |
| Rbin64_Y | MN (Hz) | 3.359 | 0.904 | 0.393 | 0.209 |
| SD (Hz) | 0.598 | 0.382 | 0.186 | 0.075 | |
| CV (%) | 17.8 | 42.3 | 47.3 | 35.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Lu, Z.; Yang, W.; Huang, M.; Tong, X. Dynamic Monitoring and Vibration Analysis of Ancient Bridges by Ground-Based Microwave Interferometry and the ESMD Method. Remote Sens. 2018, 10, 770. https://doi.org/10.3390/rs10050770
Liu X, Lu Z, Yang W, Huang M, Tong X. Dynamic Monitoring and Vibration Analysis of Ancient Bridges by Ground-Based Microwave Interferometry and the ESMD Method. Remote Sensing. 2018; 10(5):770. https://doi.org/10.3390/rs10050770
Chicago/Turabian StyleLiu, Xianglei, Zhao Lu, Wanxin Yang, Ming Huang, and Xiaohua Tong. 2018. "Dynamic Monitoring and Vibration Analysis of Ancient Bridges by Ground-Based Microwave Interferometry and the ESMD Method" Remote Sensing 10, no. 5: 770. https://doi.org/10.3390/rs10050770
APA StyleLiu, X., Lu, Z., Yang, W., Huang, M., & Tong, X. (2018). Dynamic Monitoring and Vibration Analysis of Ancient Bridges by Ground-Based Microwave Interferometry and the ESMD Method. Remote Sensing, 10(5), 770. https://doi.org/10.3390/rs10050770