Influences of Environmental Loading Corrections on the Nonlinear Variations and Velocity Uncertainties for the Reprocessed Global Positioning System Height Time Series of the Crustal Movement Observation Network of China
Abstract
:1. Introduction
2. Data and Methods
2.1. GPS Height Time Series
2.2. Environmental Loading Time Series
2.3. Time Series Analysis and Comparison Methods
3. Results
3.1. Quantitative Assessment of Environmental Loading Effects
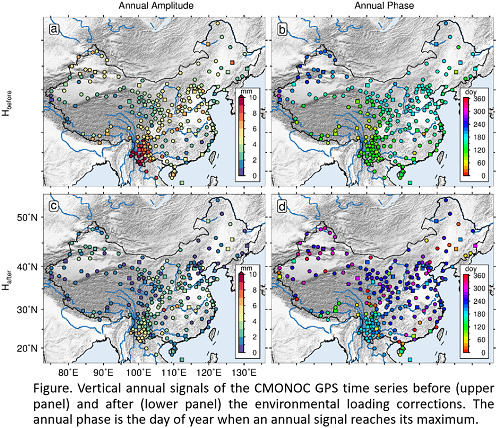
3.2. Annual Signals Analysis and Comparison
3.3. Consistency Assessment with Correlation Coefficients and RMS Reduction
3.4. Stacked Power Spectra Analysis
4. Discussion
4.1. The Effects of GFZ Loading Products on the Nonlinear Variations
4.2. The Impacts of Environmental Loading Corrections on Velocity Uncertainties
4.3. Impact of CMC Filtering on the Velocity Uncertainty
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Serpelloni, E.; Faccenna, C.; Spada, G.; Dong, D.; Williams, S.D.P. Vertical GPS ground motion rates in the Euro-Mediterranean region: New evidence of velocity gradients at different spatial scales along the Nubia-Eurasia plate boundary. J. Geophys. Res. Solid Earth 2013, 118, 6003–6024. [Google Scholar] [CrossRef] [Green Version]
- Ray, J.; Altamimi, Z.; Collilieux, X.; van Dam, T. Anomalous harmonics in the spectra of GPS position estimates. GPS Solut. 2008, 12, 55–64. [Google Scholar] [CrossRef]
- Bogusz, J.; Klos, A. On the significance of periodic signals in noise analysis of GPS station coordinates time series. GPS Solut. 2016, 20, 655–664. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallée, D. Effect of annual signals on geodetic velocity. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Bos, M.S.; Bastos, L.; Fernandes, R.M.S. The influence of seasonal signals on the estimation of the tectonic motion in short continuous GPS time-series. J. Geodyn. 2010, 49, 205–209. [Google Scholar] [CrossRef] [Green Version]
- Kaminski, P.; Figurski, M.; Kroszczynski, K.; Kroszczyński, K. Frequency and phase analysis of daily reprocessed solutions from selected EPN stations relating to geological phenomena. Acta Geodyn. Geomater. 2010, 7, 281–293. [Google Scholar]
- Bogusz, J.; Figurski, M. Annual signals observed in regional GPS networks. Acta Geodyn. Geomater. 2014, 11, 125–131. [Google Scholar] [CrossRef]
- Steigenberger, P.; Boehm, J.; Tesmer, V. Comparison of GMF/GPT with VMF1/ECMWF and implications for atmospheric loading. J. Geodesy 2009, 83, 943. [Google Scholar] [CrossRef]
- Tregoning, P.; Watson, C. Atmospheric effects and spurious signals in GPS analyses. J. Geophys. Res. 2009, 114, B09403. [Google Scholar] [CrossRef]
- Fritsche, M.; Dietrich, R.; Knöfel, C.; Rülke, A.; Vey, S.; Rothacher, M.; Steigenberger, P. Impact of higher-order ionospheric terms on GPS estimates. Geophys. Res. Lett. 2005, 32, L23311. [Google Scholar] [CrossRef]
- Petrie, E.J.; King, M.A.; Moore, P.; Lavallée, D.A. Higher-order ionospheric effects on the GPS reference frame and velocities. J. Geophys. Res. 2010, 115, B03417. [Google Scholar] [CrossRef]
- Penna, N.T.; Stewart, M.P. Aliased tidal signatures in continuous GPS height time series. Geophys. Res. Lett. 2003, 30, 2184. [Google Scholar] [CrossRef]
- Penna, N.T.; King, M.A.; Stewart, M.P. GPS height time series: Short-period origins of spurious long-period signals. J. Geophys. Res. 2007, 112, B02402. [Google Scholar] [CrossRef]
- King, M.A.; Watson, C.S. Long GPS coordinate time series: Multipath and geometry effects. J. Geophys. Res. 2010, 115, B04403. [Google Scholar] [CrossRef]
- Rodriguez-Solano, C.J.; Hugentobler, U.; Steigenberger, P.; Lutz, S. Impact of Earth radiation pressure on GPS position estimates. J. Geodesy 2012, 86, 309–317. [Google Scholar] [CrossRef]
- Collilieux, X.; van Dam, T.; Ray, J.; Coulot, D.; Métivier, L.; Altamimi, Z. Strategies to mitigate aliasing of loading signals while estimating GPS frame parameters. J. Geodesy 2012, 86, 1–14. [Google Scholar] [CrossRef]
- Van Dam, T.; Blewitt, G.; Heflin, M.B. Atmospheric pressure loading effects on Global Positioning System coordinate determinations. J. Geophys. Res. 1994, 99, 23939–23950. [Google Scholar] [CrossRef]
- Petrov, L.; Boy, J.-P. Study of the atmospheric pressure loading signal in very long baseline interferometry observations. J. Geophys. Res. 2004, 109, B03405. [Google Scholar] [CrossRef]
- Tregoning, P.; van Dam, T. Effects of atmospheric pressure loading and seven-parameter transformations on estimates of geocenter motion and station heights from space geodetic observations. J. Geophys. Res. 2005, 110, B03408. [Google Scholar] [CrossRef]
- Van Dam, T.; Altamimi, Z.; Collilieux, X.; Ray, J. Topographically induced height errors in predicted atmospheric loading effects. J. Geophys. Res. 2010, 115, B07415. [Google Scholar] [CrossRef]
- Van Dam, T.; Wahr, J.; Chao, Y.; Leuliette, E. Predictions of crustal deformation and of geoid and sea-level variability caused by oceanic and atmospheric loading. Geophys. J. Int. 1997, 129, 507–517. [Google Scholar] [CrossRef] [Green Version]
- Williams, S.D.P.; Penna, N.T. Non-tidal ocean loading effects on geodetic GPS heights. Geophys. Res. Lett. 2011, 38, L09314. [Google Scholar] [CrossRef]
- Van Dam, T.; Collilieux, X.; Wuite, J.; Altamimi, Z.; Ray, J. Nontidal ocean loading: Amplitudes and potential effects in GPS height time series. J. Geodesy 2012, 86, 1043–1057. [Google Scholar] [CrossRef]
- Van Dam, T.; Wahr, J.; Milly, P.C.D.; Shmakin, A.B.; Blewitt, G.; Lavallée, D.; Larson, K.M. Crustal displacements due to continental water loading. Geophys. Res. Lett. 2001, 28, 651–654. [Google Scholar] [CrossRef] [Green Version]
- Fritsche, M.; Döll, P.; Dietrich, R. Global-scale validation of model-based load deformation of the Earth’s crust from continental watermass and atmospheric pressure variations using GPS. J. Geodyn. 2012, 59, 133–142. [Google Scholar] [CrossRef]
- Dill, R.; Dobslaw, H. Numerical simulations of global-scale high-resolution hydrological crustal deformations. J. Geophys. Res. Solid Earth 2013, 118, 5008–5017. [Google Scholar] [CrossRef] [Green Version]
- Van Dam, T.; Böhm, J. Loading Effects and Reference Frames. In Encyclopedia of Geodesy; Grafarend, E., Ed.; Springer: Basel, Switzerland, 2016; pp. 1–5. ISBN 978-3-319-02370-0. [Google Scholar]
- Yan, H.; Chen, W.; Zhu, Y.; Zhang, W.; Zhong, M. Contributions of thermal expansion of monuments and nearby bedrock to observed GPS height changes. Geophys. Res. Lett. 2009, 36, L13301. [Google Scholar] [CrossRef]
- Wang, M.; Shen, Z.; Dong, D. Effects of non-tectonic crustal deformation on continuous GPS position time series and correction to them. Chin. J. Geophys. 2005, 48, 1045–1052. (In Chinese) [Google Scholar] [CrossRef]
- Jiang, W.; Li, Z.; Liu, H.; Zhao, Q. Cause analysis of the non-Linear variations of the IGS reference station coordinate time series in China. Chin. J. Geophys. 2013, 56, 340–351. (In Chinese) [Google Scholar] [CrossRef]
- Gu, Y.; Yuan, L.; Fan, D.; You, W.; Su, Y. Seasonal crustal vertical deformation induced by environmental mass loading in mainland China derived from GPS, GRACE and surface loading models. Adv. Space Res. 2017, 59, 88–102. [Google Scholar] [CrossRef]
- Jiang, W.; Li, Z.; van Dam, T.; Ding, W. Comparative analysis of different environmental loading methods and their impacts on the GPS height time series. J. Geodesy 2013, 87, 687–703. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Mémin, A. Geodetic secular velocity errors due to interannual surface loading deformation. Geophys. J. Int. 2015, 202, 763–767. [Google Scholar] [CrossRef] [Green Version]
- Klos, A.; Gruszczynska, M.; Bos, M.S.; Boy, J.-P.; Bogusz, J. Estimates of vertical velocity errors for IGS ITRF2014 stations by applying the improved singular spectrum analysis method and environmental loading models. Pure Appl. Geophys. 2017, 1–18. [Google Scholar] [CrossRef]
- Gu, G.-H.; Zhang, J.; Wang, W.-X. Time series of the horizontal displacement vectors at fiducial stations in the Crustal Movement Observation Network of China. Earthquake 2003, 23, 39–47. (In Chinese) [Google Scholar]
- Lou, J.; Chen, K.; Li, M.; Li, W. CMONOC fiducial station deformation before and after the Tohoku-Oki earthquake. Wuhan Daxue Xuebao (Xinxi Kexue Ban)/Geomat. Inf. Sci. Wuhan Univ. 2013, 39, 56–59. (In Chinese) [Google Scholar] [CrossRef]
- Jiang, W.; Xia, C.; Li, Z.; Guo, Q.; Zhang, S. Analysis of environmental loading effects on regional GPS coordinate time series. Cehui Xuebao/Acta Geodesy Cartogr. Sin. 2014, 43, 1217–1223. (In Chinese) [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, X.; Deng, L.; Wang, K.; Zhou, B. Quantitative analysis of geophysical sources of common mode component in CMONOC GPS coordinate time series. Adv. Space Res. 2017, 60, 2896–2909. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, Q.; Zhang, B.; Wu, W. Characterizing the Seasonal Crustal Motion in Tianshan Area Using GPS, GRACE and Surface Loading Models. Remote Sens. 2017, 9, 1303. [Google Scholar] [CrossRef]
- Wu, W.; Wu, J.; Meng, G. A Study of Rank Defect and Network Effect in Processing the CMONOC Network on Bernese. Remote Sens. 2018, 10, 357. [Google Scholar] [CrossRef]
- Li, W.; Shen, Y. The Consideration of Formal Errors in Spatiotemporal Filtering Using Principal Component Analysis for Regional GNSS Position Time Series. Remote Sens. 2018, 10, 534. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; McClusky, S.C. Introduction to GAMIT/GLOBK; Massachusetts Institute of Technology: Cambridge, MA, USA, 2013. [Google Scholar]
- Jiang, W.; Yuan, P.; Chen, H.; Cai, J.; Li, Z.; Chao, N.; Sneeuw, N. Annual variations of monsoon and drought detected by GPS: A case study in Yunnan, China. Sci. Rep. 2017, 7, 5874. [Google Scholar] [CrossRef] [PubMed]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. 2006, 111, B02406. [Google Scholar] [CrossRef]
- Simmons, A.J.; Gibson, J. The ERA-40 Project Plan; European Centre for Medium-Range Weather Forecasts: Reading, UK, 2000. [Google Scholar]
- Finlay, C.C.; Maus, S.; Beggan, C.D.; Bondar, T.N.; Chambodut, A.; Chernova, T.A.; Chulliat, A.; Golovkov, V.P.; Hamilton, B.; Hamoudi, M.; et al. International Geomagnetic Reference Field: The eleventh generation. Geophys. J. Int. 2010, 183, 1216–1230. [Google Scholar] [CrossRef] [Green Version]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System; Institut für Geodäsie und Photogrammetrie, Technische Hochschule Zürich: Zürich, Switzerland, 1999; Volume 59. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions (2010); Bureau International des Poids et Mesures Sevres (France): Sèvres, France, 2010. [Google Scholar]
- Kennett, B.L.N.; Engdahl, E.R.; Buland, R. Constraints on seismic velocities in the Earth from traveltimes. Geophys. J. Int. 1995, 122, 108–124. [Google Scholar] [CrossRef] [Green Version]
- Marsland, S.J.; Haak, H.; Jungclaus, J.H.; Latif, M.; Röske, F. The Max-Planck-Institute global ocean/sea ice model with orthogonal curvilinear coordinates. Ocean Model. 2003, 5, 91–127. [Google Scholar] [CrossRef] [Green Version]
- Dill, R. Hydological Model LSDM for Operational Earth Rotation and Gravity Field Variations; Scientific Technical Report STR08/09; GFZ: Potsdam, Germany, 2008. [Google Scholar]
- Bevis, M.; Brown, A. Trajectory models and reference frames for crustal motion geodesy. J. Geodesy 2014, 88, 283–311. [Google Scholar] [CrossRef] [Green Version]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast error analysis of continuous GNSS observations with missing data. J. Geodesy 2013, 87, 351–360. [Google Scholar] [CrossRef]
- Williams, S.D.P.; Bock, Y.; Fang, P.; Jamason, P.; Nikolaidis, R.M.; Prawirodirdjo, L.; Miller, M.; Johnson, D.J. Error analysis of continuous GPS position time series. J. Geophys. Res. 2004, 109, B03412. [Google Scholar] [CrossRef]
- Langbein, J. Noise in GPS displacement measurements from Southern California and Southern Nevada. J. Geophys. Res. 2008, 113, B05405. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Webb, F.; Prawirodirdjo, L.; Kedar, S.; Jamason, P. Spatiotemporal filtering using principal component analysis and Karhunen-Loeve expansion approaches for regional GPS network analysis. J. Geophys. Res. 2006, 111, B03405. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Krystek, M.; Anton, M. A least-squares algorithm for fitting data points with mutually correlated coordinates to a straight line. Meas. Sci. Technol. 2011, 22, 035101. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II-Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. 1982, 263, 835–853. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in Fortran 77: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1992; ISBN 978-0-521-43064-7. [Google Scholar]
- Wdowinski, S.; Bock, Y.; Zhang, J.; Fang, P.; Genrich, J. Southern California permanent GPS geodetic array: Spatial filtering of daily positions for estimating coseismic and postseismic displacements induced by the 1992 Landers earthquake. J. Geophys. Res. 1997, 102, 18057–18070. [Google Scholar] [CrossRef] [Green Version]














| CMC-filtered | CMC-filtered | |||
|---|---|---|---|---|
| κ | −0.8 ± 0.1 | −1.2 ± 0.2 | −0.7 ± 0.3 | −0.8 ± 0.3 |
| (mm/year) | 0.9 ± 0.3 | 1.2 ± 0.5 | 0.4 ± 0.3 | 0.4 ± 0.4 |
| VD (mm/year) | - | 0.1 ± 0.4 | −0.1 ± 0.3 | 0.1 ± 0.4 |
| DP | - | 1.4 ± 0.5 | 0.5 ± 0.3 | 0.4 ± 0.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, P.; Li, Z.; Jiang, W.; Ma, Y.; Chen, W.; Sneeuw, N. Influences of Environmental Loading Corrections on the Nonlinear Variations and Velocity Uncertainties for the Reprocessed Global Positioning System Height Time Series of the Crustal Movement Observation Network of China. Remote Sens. 2018, 10, 958. https://doi.org/10.3390/rs10060958
Yuan P, Li Z, Jiang W, Ma Y, Chen W, Sneeuw N. Influences of Environmental Loading Corrections on the Nonlinear Variations and Velocity Uncertainties for the Reprocessed Global Positioning System Height Time Series of the Crustal Movement Observation Network of China. Remote Sensing. 2018; 10(6):958. https://doi.org/10.3390/rs10060958
Chicago/Turabian StyleYuan, Peng, Zhao Li, Weiping Jiang, Yifang Ma, Wu Chen, and Nico Sneeuw. 2018. "Influences of Environmental Loading Corrections on the Nonlinear Variations and Velocity Uncertainties for the Reprocessed Global Positioning System Height Time Series of the Crustal Movement Observation Network of China" Remote Sensing 10, no. 6: 958. https://doi.org/10.3390/rs10060958
APA StyleYuan, P., Li, Z., Jiang, W., Ma, Y., Chen, W., & Sneeuw, N. (2018). Influences of Environmental Loading Corrections on the Nonlinear Variations and Velocity Uncertainties for the Reprocessed Global Positioning System Height Time Series of the Crustal Movement Observation Network of China. Remote Sensing, 10(6), 958. https://doi.org/10.3390/rs10060958