Winter Wheat Production Estimation Based on Environmental Stress Factors from Satellite Observations
Abstract
:1. Introduction
2. Materials
2.1. Study Area
2.2. Remote Sensing Data
2.3. Field Data
2.4. Analyses of Field- and Satellite-Level Data
2.5. Winter Wheat Planting Area Dataset
3. Methodology
3.1. The Schema of Research Procedure
3.2. The Modified Ratio Vegetation Index (MRVI) for Detecting Wheat Canopy Cab
3.3. GPP Estimation Model Based on LUE and Environmental Factors
3.4. DAM and Yield Estimation for Winter Wheat
3.5. Verificaiton of Model and New Index
4. Results
4.1. Variation of Leaf Chlorophyll Content (Cab), Total Nitrogen Content (TN), and Canopy Spectrum at Different N Level
4.2. Validation of the Modified Ratio Vegetation Index (MRVI)
4.3. Evaluation of DAM of Winter Wheat at Field Scale
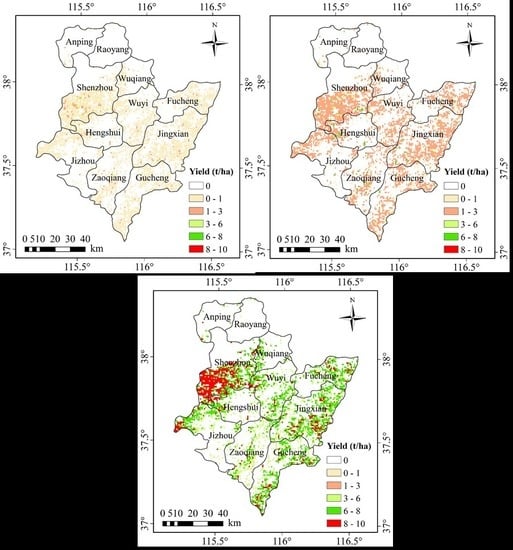
4.4. Evaluation of Winter Wheat Yield at Field Scale
5. Discussion
6. Conclusions
- We developed the new modified ratio vegetation index (MRVI), which could reveal the detailed spatiotemporal distribution of the leaf Cab and N status of the winter wheat in Hengshui City.
- We newly developed the ACPM for the winter wheat productivity estimation based on light-use efficiency theory and environmental stress factors from the Himawari-8 and MODIS satellite observations. This model described the joint effects of heat, soil moisture, and N on the crop photosynthesis performance. The ACPM model used a quantic additivity of the environmental factors in order to improve the minimum form or multiple multiplication form in the previous models. The light was determined from the MODIS FPAR data and Himawari-8 PAR data. The heat was determined from the MODIS LST data. The soil moisture was obtained from the inversion, using a visible and shortwave infrared drought index (VSDI). The N stress of the winter wheat was detected using MRVI.
- Based on the newly developed GPP model (ACPM), the DAM and yield were well estimated within a 10% and 12% error of the situ data in Hengshui City in 2017. Comparing the DAM and yield results based on the ACPM, GPP1, and GPP2 models, the ACPM model improved the underestimation of the DAM and yield results, based on the previous GPP1 and GPP2 models.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Food and Agriculture Organization of the United Nations (FAO). FAO Statistical Databases. 2014. Available online: http://faostat.fao.org (accessed on 28 November 2017).
- Food and Agriculture Organization of the United Nations (FAO). FAO Statistical Databases. 2012. Available online: http://faostat.fao.org (accessed on 4 April 2012).
- Becker-Reshef, I.; Vermote, E.; Lindeman, M.; Justice, C. A generalized regression-based model for forecasting winter wheat yields in Kansas and Ukraine using MODIS data. Remote Sens. Environ. 2010, 114, 1312–1323. [Google Scholar] [CrossRef]
- Thorp, K.R.; Wang, G.; West, A.L.; Moran, M.S.; Bronson, K.F.; White, J.W.; Mon, J. Estimating crop biophysical properties from remote sensing data by inverting linked radiative transfer and ecophysiological models. Remote Sens. Environ. 2012, 124, 224–233. [Google Scholar] [CrossRef] [Green Version]
- Atzberger, C. Advances in remote sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens. 2013, 5, 949–981. [Google Scholar] [CrossRef]
- Bognár, P.; Kern, A.; Pásztor, S.; Lichtenberger, J.; Koronczay, D.; Ferencz, C. Yield estimation and forecasting for winter wheat in hungary using time series of MODIS data. Int. J. Remote Sens. 2017, 38, 3394–3414. [Google Scholar] [CrossRef]
- Wall, L.; Larocque, D.; Léger, P.M. The early explanatory power of NDVI in crop yield modelling. Int. J. Remote Sens. 2008, 29, 2211–2225. [Google Scholar] [CrossRef]
- Curnel, Y.; Ajw, D.W.; Duveiller, G.; Defourny, P. Potential performances of remotely sensed LAI assimilation in WOFOST model based on an OSS experiment. Agric. For. Meteorol. 2011, 151, 1843–1855. [Google Scholar] [CrossRef]
- Dente, L.; Satalino, G.; Mattia, F.; Rinaldi, M. Assimilation of leaf area index derived from ASAR and MERIS data into CERES-wheat model to map wheat yield. Remote Sens. Environ. 2008, 112, 1395–1407. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S.; Hoogenboom, G. Integration of MODIS LAI and vegetation index products with the CSM-CERES-Maize model for corn yield estimation. Int. J. Remote Sens. 2011, 32, 1039–1065. [Google Scholar] [CrossRef]
- Huang, J.; Tian, L.; Liang, S.; Ma, H.; Becker-Reshef, I.; Huang, Y.; Su, W.; Zhang, X.; Zhu, D.; Wu, W. Improving winter wheat yield estimation by assimilation of the leaf area index from landsat TM and MODIS data into the WOFOST model. Agric. For. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef]
- Anderson, M.C.; Zolin, C.A.; Sentelhas, P.C.; Hain, C.R.; Semmens, K.; Yilmaz, M.T.; Gao, F.; Otkin, J.A.; Tetrault, R. The evaporative stress index as an indicator of agricultural drought in Brazil: An assessment based on crop yield impacts. Remote Sens. Environ. 2016, 174, 82–99. [Google Scholar] [CrossRef]
- Baret, F.; Weiss, M.; Troufleau, D.; Prevot, L.; Combal, B.; Bryson, R.J.E.A. Maximum information exploitation for canopy characterization by remote sensing. Asp. Appl. Biol. 2000, 60, 71–82. [Google Scholar]
- Reynolds, C.A.; Yitayew, M.; Slack, D.C.; Hutchinson, C.F.; Huete, A.; Petersen, M.S. Estimating crop yields and production by integrating the FAO crop specific water balance model with real-time satellite data and ground-based ancillary data. Int. J. Remote Sens. 2000, 21, 3487–3508. [Google Scholar] [CrossRef]
- Peñabarragán, J.M.; Lópezgranados, F.; Juradoexpósito, M.; Garcíatorres, L. Sunflower yield related to multi-temporal aerial photography, land elevation and weed infestation. Precis. Agric. 2010, 11, 568–585. [Google Scholar] [CrossRef]
- Casa, R.; Varella, H.; Buis, S.; Guérif, M.; De Solan, B.; Baret, F. Forcing a wheat crop model with LAI data to access agronomic variables: Evaluation of the impact of model and LAI uncertainties and comparison with an empirical approach. Eur. J. Agron. 2012, 37, 1–10. [Google Scholar] [CrossRef]
- Castaldi, F.; Casa, R.; Pelosi, F.; Yang, H. Influence of acquisition time and resolution on wheat yield estimation at the field scale from canopy biophysical variables retrieved from spot satellite data. Int. J. Remote Sens. 2015, 36, 2438–2459. [Google Scholar] [CrossRef]
- Ferencz, C.; Bognár, P.; Lichtenberger, J.; Hamar, D.; Tarcsai, G.; Timár, G.; Molnár, G.; Pásztor, S.; Steinbach, P.; Székely, B. Crop yield estimation by satellite remote sensing. Int. J. Remote Sens. 2004, 25, 4113–4149. [Google Scholar] [CrossRef]
- Prasad, A.K.; Chai, L.; Singh, R.P.; Kafatos, M. Crop yield estimation model for Iowa using remote sensing and surface parameters. Int. J. Appl. Earth Obs. 2006, 8, 26–33. [Google Scholar] [CrossRef]
- Salazar, L.; Kogan, F.; Roytman, L. Use of remote sensing data for estimation of winter wheat yield in the United States. Int. J. Remote Sens. 2007, 28, 3795–3811. [Google Scholar] [CrossRef]
- Shanahan, J.F.; Schepers, J.S.; Francis, D.D.; Varvel, G.E.; Wilhelm, W.W.; Tringe, J.M.; Schlemmer, M.R.; Major, D.J. Use of remote-sensing imagery to estimate corn grain yield. Agron. J. 2001, 93, 583–589. [Google Scholar] [CrossRef]
- Son, N.T.; Chen, C.F.; Chen, C.R.; Chang, L.Y.; Duc, H.N.; Nguyen, L.D. Prediction of rice crop yield using MODIS EVI−LAI data in the mekong delta, vietnam. Int. J. Remote Sens. 2013, 34, 7275–7292. [Google Scholar] [CrossRef]
- Bala, S.K.; Islam, A.S. Correlation between potato yield and MODIS-derived vegetation indices. Int. J. Remote Sens. 2009, 30, 2491–2507. [Google Scholar] [CrossRef]
- Ren, J.; Chen, Z.; Zhou, Q.; Tang, H. Regional yield estimation for winter wheat with MODIS-NDVI data in Shandong, China. Int. J. Appl. Earth Obs. 2008, 10, 403–413. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.F.; Becker-Reshef, I.; Claverie, M.; Huang, J.; Zhang, J.; Justice, C.; Sobrino, J.A. Improving the timeliness of winter wheat production forecast in the United States of America, Ukraine and China using MODIS data and NCAR growing degree day information. Remote Sens. Environ. 2015, 161, 131–148. [Google Scholar] [CrossRef]
- Sakamoto, T.; Gitelson, A.A.; Arkebauer, T.J. MODIS-based corn grain yield estimation model incorporating crop phenology information. Remote Sens. Environ. 2013, 131, 215–231. [Google Scholar] [CrossRef]
- Kussul, N.; Kogan, F.; Adamenko, T.I.; Skakun, S.V.; Kravchenko, A.N.; Krivobok, A.A.; Shelestov, A.Y.; Kolotii, A.V.; Kussul, O.M.; Lavrenyuk, A.N. Winter wheat yield forecasting: A comparative analysis of results of regression and biophysical models. J. Autom. Inf. Sci. 2013, 45, 68–81. [Google Scholar] [CrossRef]
- Moriondo, M.; Maselli, F.; Bindi, M. A simple model of regional wheat yield based on NDVI data. Eur. J. Agron. 2007, 26, 266–274. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; van der Heijden, G.W.A.M.; Verzakov, S.; Schaepman, M.E. Estimating grassland biomass using SVM band shaving of hyperspectral data. Photogramm. Eng. Remote Sens. 2007, 73, 1141–1148. [Google Scholar] [CrossRef]
- Porter, J.R.; Jamieson, P.D.; Wilson, D.R. Comparison of the wheat simulation models AFRCWHEAT2, CERES-wheat and SWHEAT for non-limiting conditions of crop growth. Field Crops Res. 1993, 33, 131–157. [Google Scholar] [CrossRef]
- Prince, S.D.; Goward, S.N. Global primary production: A remote sensing approach. J. Biogeogr. 1995, 22, 815–835. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Iii, B.M. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Lo Seen, D.; Mougin, E.; Rambal, S.; Gaston, A.; Hiernaux, P. A regional sahelian grassland model to be coupled with multispectral satellite data. II: Toward the control of its simulations by remotely sensed indices. Remote Sens. Environ. 1995, 52, 194–206. [Google Scholar] [CrossRef]
- Li, A.; Bian, J.; Lei, G.; Huang, C. Estimating the maximal light use efficiency for different vegetation through the casa model combined with time-series remote sensing data and ground measurements. Remote Sens. 2012, 4, 3857–3876. [Google Scholar] [CrossRef]
- Faivre, R.; Leenhardt, D.; Voltz, M.; Benoît, M.; Papy, F.; Dedieu, G.; Wallach, D. Spatialising crop models. Agronomie 2004, 24, 205–217. [Google Scholar] [CrossRef]
- Claverie, M.; Demarez, V.; Duchemin, B.; Hagolle, O.; Ducrot, D.; Marais-Sicre, C.; Dejoux, J.F.; Huc, M.; Keravec, P.; Béziat, P.; et al. Maize and sunflower biomass estimation in southwest France using high spatial and temporal resolution remote sensing data. Remote Sens. Environ. 2012, 124, 844–857. [Google Scholar] [CrossRef] [Green Version]
- Asseng, S.; Foster, I.; Turner, N.C. The impact of temperature variability on wheat yields. Glob. Chang. Biol. 2011, 17, 997–1012. [Google Scholar] [CrossRef]
- Lobell, D.B.; Schlenker, W.; Costaroberts, J. Climate trends and global crop production since 1980. Science 2011, 333, 616–620. [Google Scholar] [CrossRef] [PubMed]
- Peng, G.; Yin, Y.; Yu, C. China: Invest wisely in sustainable water use. Science 2011, 331, 1264–1265. [Google Scholar] [CrossRef]
- Jiang, Z.; Chen, Z.; Chen, J.; Ren, J.; Li, Z.; Sun, L. The estimation of regional crop yield using ensemble-based four-dimensional variational data assimilation. Remote Sens. 2014, 6, 2664–2681. [Google Scholar] [CrossRef]
- Wu, K.; Huang, R.J. The sustainable evaluations, the development potentialities and the countermeasures of water and land resources use in the Huang-Huai-Hai plain. Sci. Geogr. Sin. 2001, 5, 390–395. [Google Scholar]
- Carfagna, E.; Gallego, F.J. Using remote sensing for agricultural statistics. Int. Stat. Rev. 2005, 73, 389–404. [Google Scholar] [CrossRef]
- Xue, L.; Cao, W.; Luo, W.; Dai, T.; Zhu, Y. Monitoring leaf nitrogen status in rice with canopy spectral reflectance. Agron. J. 2004, 96, 135–142. [Google Scholar] [CrossRef]
- Zhang, N. Crop Yield Estimation Using Remote Sensing Technology Based on Four Environmental Factors: Radiation, Temperature, Moisture and Nutrition with Case Study on Wheat and Corn. Ph.D. Thesis, Peking University, Beijing, China, 2013. [Google Scholar]
- Gower, S.T.; Kucharik, C.J.; Norman, J.M. Direct and indirect estimation of leaf area index, fAPAR, and net primary production of terrestrial ecosystems. Remote Sens. Environ. 1999, 70, 29–51. [Google Scholar] [CrossRef]
- Peng, Y.; Gitelson, A.A.; Sakamoto, T. Remote estimation of gross primary productivity in crops using MODIS 250 m data. Remote Sens. Environ. 2013, 128, 186–196. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide dynamic range vegetation index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165. [Google Scholar] [CrossRef] [PubMed]
- Bradford, J.B.; Hicke, J.A.; Lauenroth, W.K. The relative importance of light-use efficiency modifications from environmental conditions and cultivation for estimation of large-scale net primary productivity. Remote Sens. Environ. 2005, 96, 246–255. [Google Scholar] [CrossRef]
- Lobell, D.B.; Hicke, J.A.; Asner, G.P.; Field, C.B.; Tucker, C.J.; Los, S.O. Satellite estimates of productivity and light use efficiency in United States agriculture, 1982–98. Glob. Chang. Biol. 2002, 8, 722–735. [Google Scholar] [CrossRef]
- Gough, C. Terrestrial primary production: Fuel for life. Nat. Educ. Knowl. 2012, 3, 28. [Google Scholar]
- Prince, S.D.; Haskett, J.; Steininger, M.; Strand, H.; Wright, R. Net primary production of U.S. Midwest croplands from agricultural harvest yield data. Ecol. Appl. 2001, 11, 1194–1205. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr. Monitoring the Vernal Advancement and Retrogradation (Greenwave Effect) of Natural Vegetation; NASA/GSFCT Type Report; NASA: Washington, DC, USA, 1973.
- Huete, A.; Justice, C.; Liu, H. Development of vegetation and soil indices for MODIS-EOS. Remote Sens. Environ. 1994, 49, 224–234. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Roujean, J.L.; Breon, F.M. Estimating par absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Reyniers, M.; Walvoort, D.J.J.; Baardemaaker, J.D. A linear model to predict with a multi-spectral radiometer the amount of nitrogen in winter wheat. Int. J. Remote Sens. 2006, 27, 4159–4179. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Verrelst, J.; Schaepman, M.E.; Koetz, B.; Kneubühler, M. Angular sensitivity analysis of vegetation indices derived from chris/proba data. Remote Sens. Environ. 2008, 112, 2341–2353. [Google Scholar] [CrossRef]
- Zhu, Y.; Yao, X.; Tian, Y.C.; Liu, X.J.; Cao, W.X. Analysis of common canopy vegetation indices for indicating leaf nitrogen accumulations in wheat and rice. Int. J. Appl. Earth Obs. 2008, 10, 1–10. [Google Scholar] [CrossRef]
- Schleicher, T.D.; Bausch, W.C.; Delgado, J.A.; Ayers, P.D. Evaluation and refinement of the nitrogen reflectance index (NRI) for site-specific fertilizer management. In 2001 ASAE Annual Meeting; American Society of Agricultural and Biological Engineers: St. Joseph County, IN, USA, 1998. [Google Scholar]
- Ranjan, R.; Chopra, U.K.; Sahoo, R.N.; Singh, A.K.; Pradhan, S. Assessment of plant nitrogen stress in wheat (Triticum aestivum L.) through hyperspectral indices. Int. J. Remote Sens. 2012, 33, 6342–6360. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; Colstoun, E.B.D.; Mcmurtrey, J.E., III. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf-area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Penuelas, J.; Baret, F.; Filella, I. Semiempirical indexes to assess carotenoids chlorophyll-a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Zarco-Tejada, P.J.; Berjón, A.; López-Lozano, R.; Miller, J.R.; Martín, P.; Cachorro, V.; González, M.R.; Frutos, A.D. Assessing vineyard condition with hyperspectral indices: Leaf and canopy reflectance simulation in a row-structured discontinuous canopy. Remote Sens. Environ. 2005, 99, 271–287. [Google Scholar] [CrossRef]
- Genovese, G.; Vignolles, C.; Nègre, T.; Passera, G. A methodology for a combined use of normalised difference vegetation index and CORINE land cover data for crop yield monitoring and forecasting. A case study on Spain. Agronomie 2001, 21, 91–111. [Google Scholar] [CrossRef]
- Yao, F.; Feng, L.; Zhang, J. Corn area extraction by the integration of MODIS-EVI time series data and China’s environment satellite (HJ-1) data. J. Indian Soc. Remote 2014, 42, 859–867. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, L.; Yao, F. Improved maize cultivated area estimation over a large scale combining MODIS–EVI time series data and crop phenological information. ISPRS J. Photogramm. 2014, 94, 102–113. [Google Scholar] [CrossRef]
- Delegido, J.; Alonso, L.; González, G.; Moreno, J. Estimating chlorophyll content of crops from hyperspectral data using a normalized area over reflectance curve (NAOC). Int. J. Appl. Earth Obs. 2006, 12, 165–174. [Google Scholar] [CrossRef]
- Vincini, M.; Calegari, F.; Casa, R. Sensitivity of leaf chlorophyll empirical estimators obtained at sentinel-2 spectral resolution for different canopy structures. Precis. Agric. 2016, 17, 313–331. [Google Scholar] [CrossRef]
- Houborg, R.; Anderson, M.; Daughtry, C. Utility of an image-based canopy reflectance modeling tool for remote estimation of LAI and leaf chlorophyll content at the field scale. Remote Sens. Environ. 2009, 113, 259–274. [Google Scholar] [CrossRef]
- Li, Z.; Jin, X.; Wang, J.; Yang, G.; Nie, C.; Xu, X.; Feng, H. Estimating winter wheat (Triticum aestivum) LAI and leaf chlorophyll content from canopy reflectance data by integrating agronomic prior knowledge with the prosail model. Int. J. Remote Sens. 2015, 36, 2634–2653. [Google Scholar] [CrossRef]
- Wang, P.; Sun, R.; Zhang, J.; Zhou, Y.; Xie, D.; Zhu, Q. Yield estimation of winter wheat in the north china plain using the remote-sensing–photosynthesis–yield estimation for crops (RS–P–VEC) model. Int. J. Remote Sens. 2011, 32, 6335–6348. [Google Scholar] [CrossRef]
- Fei, T.; Wu, W.; Li, D.; Chen, Z.; Huang, Q.; Tian, X. Yield estimation of winter wheat in North China Plain by using crop growth monitoring system (CGMS). In Proceedings of the International Conference on Agro-Geoinformatic, Shanghai, China, 2–4 August 2012. [Google Scholar]
- Son, N.T.; Chen, C.F.; Chen, C.R.; Minh, V.Q.; Trung, N.H. A comparative analysis of multitemporal MODIS EVI and NDVI data for large-scale rice yield estimation. Agric. For. Meteorol. 2014, 197, 52–64. [Google Scholar] [CrossRef]
- Jégo, G.; Pattey, E.; Liu, J. Using leaf area index, retrieved from optical imagery, in the STICS crop model for predicting yield and biomass of field crops. Field Crops Res. 2012, 131, 63–74. [Google Scholar] [CrossRef]
- Zhao, C.; Bao, Y.; Cheng, M.; Huang, W.; Liu, L. Use of landsat TM and EOS MODIS imaging technologies for estimation of winter wheat yield in the north China plain. Int. J. Remote Sens. 2012, 33, 1029–1041. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop J. 2016, 4, 212–219. [Google Scholar] [CrossRef]
- Fu, Y.; Yang, G.; Wang, J.; Song, X.; Feng, H. Winter wheat biomass estimation based on spectral indices, band depth analysis and partial least squares regression using hyperspectral measurements. Comput. Electron. Agric. 2014, 100, 51–59. [Google Scholar] [CrossRef]
- Liaqat, M.U.; Cheema, M.J.M.; Huang, W.; Mahmood, T.; Zaman, M.; Khan, M.M. Evaluation of MODIS and landsat multiband vegetation indices used for wheat yield estimation in irrigated Indus Basin. Comput. Electron. Agric. 2017, 138, 39–47. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Yang, G.; Yang, H.; Feng, H.; Xu, X.; Wang, J.; Li, X.; Luo, J. Winter wheat yield estimation based on multi-source medium resolution optical and radar imaging data and the aquacrop model using the particle swarm optimization algorithm. ISPRS J. Photogramm. 2017, 126, 24–37. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, P.; Bai, X.; Khan, J.; Zhang, S.; Li, L.; Wang, L. Assimilation of the leaf area index and vegetation temperature condition index for winter wheat yield estimation using landsat imagery and the CERES-wheat model. Agric. For. Meteorol. 2017, 246, 194–206. [Google Scholar] [CrossRef]
- Mokhtari, A.; Noory, H.; Vazifedoust, M. Improving crop yield estimation by assimilating LAI and inputting satellite-based surface incoming solar radiation into SWAP model. Agric. For. Meteorol. 2018, 250–251, 159–170. [Google Scholar] [CrossRef]
















| Experiment | Year | Location | Measurement | |
|---|---|---|---|---|
| Content | Date | |||
| exp1 | 2011 | Yucheng, Shandong province, China. | Soil moisture, leaf water content, spectral reflectance, chlorophyll content, and total nitrogen content. | 28 March 2011 7 April 2011 14 April 2011 19 April 2011 24 April 2011 7 May 2011 12 May 2011 19 May 2011 24 May 2011 |
| exp2 | 2017 | Hengshui, Hebei province, China. | Soil moisture, spectral reflectance, chlorophyll content, and dry aboveground biomass yield. | 29 March 2017 5 May 2017 31 May 2017 |
| Sentinel-2 | ||||
|---|---|---|---|---|
| Winter Wheat | Non-Wheat | Total | ||
| Worldview2 | Winter Wheat | 144 | 6 | 150 |
| Non-Wheat | 7 | 43 | 50 | |
| Total | 151 | 49 | 200 | |
| Overall accuracy = 100 × (144 + 43)/200 = 93.5% | ||||
| Producer’s accuracy | Omission error | User’s accuracy | Commission error | |
| Winter wheat | 100 × 144/151 = 95.36% | 4.64% | 100 × 144/150 = 96% | 4% |
| Indexes | Expressions | Literaries | R2 | RMSE |
|---|---|---|---|---|
| NDVI | [52] | 0.4 | 10.38 | |
| VI | [53] | 0.47 | 9.75 | |
| SAVI | [54] | 0.45 | 9.95 | |
| MSAVI | [55] | 0.49 | 9.64 | |
| OSAVI | [56] | 0.43 | 10.12 | |
| WDRVI | [47] | 0.5 | 9.49 | |
| RDVI | [57] | 0.45 | 9.98 | |
| MSR | [58] | 0.52 | 9.27 | |
| Viopt | [59] | 0.45 | 9.94 | |
| GNDVI | [60] | 0.51 | 9.43 | |
| NDVIg-b | [61] | 0.11 | 12.67 | |
| RVI1 | [62] | 0.51 | 9.38 | |
| RVI2 | [43] | 0.59 | 8.66 | |
| NRI | [63] | 0.28 | 11.39 | |
| NPCI | [64] | 0.34 | 10.96 | |
| MCARI | [65] | 0.47 | 9.82 | |
| New Index | 0.54 | 9.08 | ||
| DVI | [66] | 0.47 | 9.82 | |
| PSRI | [67] | 0.02 | 13.3 | |
| SIPI | [68] | 0.52 | 9.35 | |
| GI | [69] | 0.41 | 10.32 | |
| SRPI | [68] | 0.44 | 10.07 | |
| MRVI | 0.62 | 8.34 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sui, J.; Qin, Q.; Ren, H.; Sun, Y.; Zhang, T.; Wang, J.; Gong, S. Winter Wheat Production Estimation Based on Environmental Stress Factors from Satellite Observations. Remote Sens. 2018, 10, 962. https://doi.org/10.3390/rs10060962
Sui J, Qin Q, Ren H, Sun Y, Zhang T, Wang J, Gong S. Winter Wheat Production Estimation Based on Environmental Stress Factors from Satellite Observations. Remote Sensing. 2018; 10(6):962. https://doi.org/10.3390/rs10060962
Chicago/Turabian StyleSui, Juan, Qiming Qin, Huazhong Ren, Yuanheng Sun, Tianyuan Zhang, Jiandong Wang, and Shihong Gong. 2018. "Winter Wheat Production Estimation Based on Environmental Stress Factors from Satellite Observations" Remote Sensing 10, no. 6: 962. https://doi.org/10.3390/rs10060962
APA StyleSui, J., Qin, Q., Ren, H., Sun, Y., Zhang, T., Wang, J., & Gong, S. (2018). Winter Wheat Production Estimation Based on Environmental Stress Factors from Satellite Observations. Remote Sensing, 10(6), 962. https://doi.org/10.3390/rs10060962