Inland Water Atmospheric Correction Based on Turbidity Classification Using OLCI and SLSTR Synergistic Observations
Abstract
:1. Introduction
2. Study Area and Data
2.1. Overview of the Study Area
2.2. Data and Processing
2.2.1. Image and Preprocessing
2.2.2. In Situ Measurement Data
3. Procedure of the ACbTC
3.1. The Basic Theory of the Algorithm
3.2. The Processing Procedure of the ACbTC
3.2.1. Rayleigh Correction for the OLCI and SLSTR
- (1)
- The smallest rectangle containing the lake area was divided into several squares of the same size (the number of squares depends on the computing ability and the number in this study was selected as nine), and the center pixel of each square was set as the representative point (shown in the Figure 4a).
- (2)
- The corresponding auxiliary information of each point were extracted from the SLSTR dataset.
- (3)
- The 6SV model was compiled for each point to simulate the scattering process of the Rayleigh molecules in advance. Then, the Rayleigh reflectance spectrum was constructed and it was assigned to represent this square area.
- (4)
- In each square, the reflectance of the top of the atmosphere was subtracted from the Rayleigh reflectance to complete the Rayleigh scattering correction.
3.2.2. Aerosol Reflectance Calculation by Turbidity Detection
- (a)
- Exclude the boundary between water and land using the Canny filter [61] to avoid the mixed pixel contamination;
- (b)
- (c)
3.3. Accuracy Assessment
4. Results
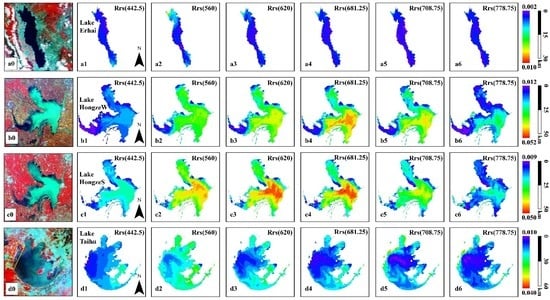
4.1. Visual Inspection of Atmospherically Corrected Images
4.2. Comparison with In Situ Measurements
4.3. Comparison with Other Atmospheric Algorithms
5. Discussion
5.1. The Usability of OL21-1020 nm for Distinguishing Turbid Water from Clean Water
5.2. The Effect of the GRA Index to Distinguish the Water Turbidity
5.3. The Necessity of Using Different Bands for Atmospheric Correction in Turbid and Clean Inland Lakes
5.4. Limitations of ACbTC in Applications
6. Conclusions
- (1)
- The GRA index is proposed to distinguish turbid inland water from clean water, which depends on the feature of the 1020 nm peak of Rrs in clean inland lakes and the decreasing slope from 885 to 1613 nm, especially for clean inland lakes that cover relatively small areas. Through the qualitative analysis of 12 inland lakes and the existing observation data, the threshold of the GRA index was determined as −0.07 in this study. The classification results of the GRA index performed better than the Diff and Tind indices for inland lakes by constraining the land adjacency effect at 1020 nm on the similar spectral shapes of turbid lakes.
- (2)
- The synergistic use of OLCI and SLSTR was verified to provide additional atmospheric correction bands, SL05-1613 nm and SL06-2250 nm, for turbid inland lakes to satisfy the dark pixel assumption. The incorrect use of atmospheric correction bands in turbid inland lakes may cause an overcorrection in the short bands due to the invalid assumption and the stray light effect. Thus, OL17 + SL05 and SL05 + SL06 are recommended for the clean and turbid inland waters, respectively. Additionally, OL21-1020 nm is unsuitable for atmospheric correction of inland lakes because it is a vulnerable band easily affected by land stray light.
- (3)
- The ACbTC method calculated the aerosol reflectance based on turbidity identification. Compared to the in situ measurements, the ACbTC algorithm achieved full-band average values of MAPE = 29.55%, MRPE = 13.98%, and RMSE = 0.0039 sr−1, which were more accurate than the C2RCC, MUMM, FLAASH, POLYMER, and BPAC. The results indicate that both the synergistic use of OLCI and SLSTR and the water turbidity classification are essential for accurate atmospheric correction in inland lakes when using Sentinel-3 data.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shi, K.; Zhang, Y.; Zhu, G.; Qin, B.; Pan, D. Deteriorating water clarity in shallow waters: Evidence from long term MODIS and in-situ observations. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 287–297. [Google Scholar] [CrossRef]
- Shutler, J.; Land, P.; Smyth, T.; Groom, S. Extending the MODIS 1 km ocean colour atmospheric correction to the MODIS 500 m bands and 500 m chlorophyll-a estimation towards coastal and estuarine monitoring. Remote Sens. Environ. 2007, 107, 521–532. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W.; Tang, J. Water property monitoring and assessment for China’s inland Lake Taihu from MODIS-Aqua measurements. Remote Sens. Environ. 2011, 115, 841–854. [Google Scholar] [CrossRef]
- Palmer, S.C.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Wang, M. Atmospheric correction for remotely-sensed ocean-colour products. In Reports and Monographs of the International Ocean-Colour Coordinating Group (IOCCG); IOCCG: Monterey, CA, USA, 2010. [Google Scholar]
- Liu, G.; Li, Y.; Lyu, H.; Wang, S.; Du, C.; Huang, C. An improved land target-based atmospheric correction method for Lake Taihu. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 793–803. [Google Scholar] [CrossRef]
- Steinmetz, F.; Deschamps, P.-Y.; Ramon, D. Atmospheric correction in presence of sun glint: Application to MERIS. Opt. Express 2011, 19, 9783–9800. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Shi, W. The NIR-SWIR combined atmospheric correction approach for MODIS ocean color data processing. Opt. Express 2007, 15, 15722–15733. [Google Scholar] [CrossRef] [PubMed]
- Gao, B.-C.; Davis, C.; Goetz, A. A review of atmospheric correction techniques for hyperspectral remote sensing of land surfaces and ocean color. In Proceedings of the IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 1979–1981. [Google Scholar]
- Ruddick, K.G.; Ovidio, F.; Rijkeboer, M. Atmospheric correction of SeaWiFS imagery for turbid coastal and inland waters. Appl. Opt. 2000, 39, 897–912. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Gordon, H.R. A simple, moderately accurate, atmospheric correction algorithm for SeaWiFS. Remote Sens. Environ. 1994, 50, 231–239. [Google Scholar] [CrossRef]
- Ahn, J.-H.; Park, Y.-J.; Ryu, J.-H.; Lee, B.; Oh, I.S. Development of atmospheric correction algorithm for Geostationary Ocean Color Imager (GOCI). Ocean Sci. J. 2012, 47, 247–259. [Google Scholar] [CrossRef]
- Moore, G.; Aiken, J.; Lavender, S. The atmospheric correction of water colour and the quantitative retrieval of suspended particulate matter in Case II waters: Application to MERIS. Int. J. Remote Sens. 1999, 20, 1713–1733. [Google Scholar] [CrossRef]
- Siegel, D.A.; Wang, M.; Maritorena, S.; Robinson, W. Atmospheric correction of satellite ocean color imagery: The black pixel assumption. Appl. Opt. 2000, 39, 3582–3591. [Google Scholar] [CrossRef] [PubMed]
- Wang, M. Study of the Sea-Viewing Wide Field-of-View Sensor (SeaWiFS) aerosol optical property data over ocean in combination with the ocean color products. J. Geophys. Res. 2005, 110, D10S06. [Google Scholar] [CrossRef]
- Ruddick, K.G.; De Cauwer, V.; Park, Y.-J.; Moore, G. Seaborne measurements of near infrared water-leaving reflectance: The similarity spectrum for turbid waters. Limnol. Oceanogr. 2006, 51, 1167–1179. [Google Scholar] [CrossRef] [Green Version]
- Carswell, T.; Costa, M.; Young, E.; Komick, N.; Gower, J.; Sweeting, R. Evaluation of MODIS-Aqua atmospheric correction and chlorophyll products of Western North American coastal waters based on 13 years of data. Remote Sens. 2017, 9, 1063. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Advantages of high quality SWIR bands for ocean colour processing: Examples from Landsat-8. Remote Sens. Environ. 2015, 161, 89–106. [Google Scholar] [CrossRef]
- Cao, F.; Tzortziou, M.; Hu, C.; Mannino, A.; Fichot, C.G.; Del Vecchio, R.; Najjar, R.G.; Novak, M. Remote sensing retrievals of colored dissolved organic matter and dissolved organic carbon dynamics in North American estuaries and their margins. Remote Sens. Environ. 2018, 205, 151–165. [Google Scholar] [CrossRef]
- Li, J.; Hu, C.; Shen, Q.; Barnes, B.B.; Murch, B.; Feng, L.; Zhang, M.; Zhang, B. Recovering low quality MODIS-Terra data over highly turbid waters through noise reduction and regional vicarious calibration adjustment: A case study in Taihu Lake. Remote Sens. Environ. 2017, 197, 72–84. [Google Scholar] [CrossRef]
- Shen, M.; Duan, H.; Cao, Z.; Xue, K.; Loiselle, S.; Yesou, H. Determination of the downwelling diffuse attenuation coefficient of lake water with the Sentinel-3A OLCI. Remote Sens. 2017, 9, 1246. [Google Scholar] [CrossRef]
- Shi, W.; Wang, M. Detection of turbid waters and absorbing aerosols for the MODIS ocean color data processing. Remote Sens. Environ. 2007, 110, 149–161. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, M.; Cui, T.; Wen, Z. A review of some important technical problems in respect of satellite remote sensing of chlorophyll-a concentration in coastal waters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2275–2289. [Google Scholar] [CrossRef]
- Wang, M.; Son, S.; Shi, W. Evaluation of MODIS SWIR and NIR-SWIR atmospheric correction algorithms using SeaBASS data. Remote Sens. Environ. 2009, 113, 635–644. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Yu, G.; Oyama, Y.; Yoshimura, K.; Fukushima, T. A hybrid algorithm for estimating the chlorophyll-a concentration across different trophic states in Asian inland waters. ISPRS J. Photogramm. Remote Sens. 2015, 102, 28–37. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Z.; Li, Y.; Guo, Y.; Xu, Y.; Liu, G.; Du, C. Landsat-based long-term monitoring of total suspended matter concentration pattern change in the wet season for Dongting Lake, China. Remote Sens. 2015, 7, 13975–13999. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, Y.; Li, K.; Huang, L.; Yang, F.; Zhou, Y.; Chang, J. Seasonal and spatial distributions of euphotic zone and long-term variations in water transparency in a clear oligotrophic Lake Fuxian, China. J. Environ. Sci. 2018. [Google Scholar] [CrossRef]
- Hou, X.; Feng, L.; Duan, H.; Chen, X.; Sun, D.; Shi, K. Fifteen-year monitoring of the turbidity dynamics in large lakes and reservoirs in the middle and lower basin of the Yangtze River, China. Remote Sens. Environ. 2017, 190, 107–121. [Google Scholar] [CrossRef]
- Knaeps, E.; Dogliotti, A.; Raymaekers, D.; Ruddick, K.; Sterckx, S. In situ evidence of non-zero reflectance in the OLCI 1020 nm band for a turbid estuary. Remote Sens. Environ. 2012, 120, 133–144. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Chen, X.; Tian, L.; Chen, L. Human induced turbidity changes in poyang lake between 2000 and 2010: Observations from MODIS. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- North, P.; Brockmann, C.; Fischer, J.; Gomez-Chova, L.; Grey, W.; Heckel, A.; Moreno, J.; Preusker, R.; Regner, P. MERIS/AATSR synergy algorithms for cloud screening, aerosol retrieval and atmospheric correction. In Proceedings of the 2nd MERIS/AATSR User Workshop, ESRIN, Frascati, Italy, 22–26 September 2008; pp. 22–26. [Google Scholar]
- Ruddick, K.; Vanhellemont, Q. Use of the new OLCI and SLSTR band for atmospheric correction over turbid coastal and inland waters. In Proceedings of the Sentinel-3 Science Workshop, Venice, Italy, 2–5 June 2015. [Google Scholar]
- Wang, M. Remote sensing of the ocean contributions from ultraviolet to near-infrared using the shortwave infrared bands: Simulations. Appl. Opt. 2007, 46, 1535–1547. [Google Scholar] [CrossRef] [PubMed]
- Bernardo, N.; Watanabe, F.; Rodrigues, T.; Alcântara, E. Evaluation of the suitability of MODIS, OLCI and OLI for mapping the distribution of total suspended matter in the Barra Bonita Reservoir (Tietê River, Brazil). Remote Sens. Appl. Soc. Environ. 2016, 4, 68–82. [Google Scholar] [CrossRef]
- Liu, G.; Simis, S.G.; Li, L.; Wang, Q.; Li, Y.; Song, K.; Lyu, H.; Zheng, Z.; Shi, K. A four-band semi-analytical model for estimating phycocyanin in inland waters from simulated MERIS and OLCI data. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1374–1385. [Google Scholar] [CrossRef]
- Lin, J.; Lyu, H.; Miao, S.; Pan, Y.; Wu, Z.; Li, Y.; Wang, Q. A two-step approach to mapping particulate organic carbon (POC) in inland water using OLCI images. Ecol. Indic. 2018, 90, 502–512. [Google Scholar] [CrossRef]
- Mecklenburg, S.; Nieke, J.; Goryl, P.; Berruti, B. Sentinel-3: Mission status and performance after one year in orbit. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 4046–4051. [Google Scholar]
- Heckel, A.; North, P.; Henocq, C.; Goryl, P.; Dransfeld, S.; Grzegorski, M. Application of AATSR aerosol retrieval to new data from SLSTR onboard Sentinel-3 satellite. In Proceedings of the 19th EGU General Assembly Conference, Vienna, Austria, 23–28 April 2017; p. 16568. [Google Scholar]
- Song, K.; Liu, D.; Li, L.; Wang, Z.; Wang, Y.; Jiang, G. Spectral absorption properties of colored dissolved organic matter (CDOM) and total suspended matter (TSM) of inland waters. Proc. SPIE 2010, 7811, 78110B. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, E.; Liu, M. Spectral absorption properties of chromophoric dissolved organic matter and particulate matter in Yunnan Palteau Lakes. J. Lake Sci. 2009, 21, 255–263. [Google Scholar]
- Cao, Z.; Duan, H.; Feng, L.; Ma, R.; Xue, K. Climate-and human-induced changes in suspended particulate matter over Lake Hongze on short and long timescales. Remote Sens. Environ. 2017, 192, 98–113. [Google Scholar] [CrossRef]
- Ping, Y. Studies on Phytoplankton and Eutrophication Status of Large and Medium-Sized Shallow Lakes in Jiangxi Province, China. Master’s Thesis, Jiangxi Normal University, Nanchang, China, 2015. [Google Scholar]
- Zhang, C.; Tian, J.; Jin, Z.; Zhao, X.; Sun, Y. The study of present situation and engineering technology processing of algae in Xingyun Lake. Environ. Sci. Surv. 2017, 36, 8–12. [Google Scholar]
- Liou, K.-N. An Introduction to Atmospheric Radiation; Elsevier: Amsterdam, The Netherlands, 2002; Volume 84. [Google Scholar]
- Gordon, H.R.; Franz, B.A. Remote sensing of ocean color: Assessment of the water-leaving radiance bidirectional effects on the atmospheric diffuse transmittance for seawifs and modis intercomparisons. Remote Sens. Environ. 2008, 112, 2677–2685. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Turbid wakes associated with offshore wind turbines observed with Landsat 8. Remote Sens. Environ. 2014, 145, 105–115. [Google Scholar] [CrossRef]
- Zheng, Z.; Ren, J.; Li, Y.; Huang, C.; Liu, G.; Du, C.; Lyu, H. Remote sensing of diffuse attenuation coefficient patterns from Landsat 8 OLI imagery of turbid inland waters: A case study of Dongting Lake. Sci. Total Environ. 2016, 573, 39–54. [Google Scholar] [CrossRef] [PubMed]
- Mueller, J.L.; Davis, C.; Arnone, R.; Frouin, R.; Carder, K.; Lee, Z.; Steward, R.; Hooker, S.; Mobley, C.D.; McLean, S. Above-water radiance and remote sensing reflectance measurements and analysis protocols. Ocean Opt. Protoc. Satell. Ocean Color Sens. Valid. Revis. 2000, 2, 98–107. [Google Scholar]
- Le, C.; Hu, C.; Cannizzaro, J.; Duan, H. Long-term distribution patterns of remotely sensed water quality parameters in Chesapeake Bay. Estuar. Coast. Shelf Sci. 2013, 128, 93–103. [Google Scholar] [CrossRef]
- Le, C.; Hu, C.; Cannizzaro, J.; English, D.; Muller-Karger, F.; Lee, Z. Evaluation of chlorophyll-a remote sensing algorithms for an optically complex estuary. Remote Sens. Environ. 2013, 129, 75–89. [Google Scholar] [CrossRef]
- Chen, J.; Fu, J.; Zhang, M. An atmospheric correction algorithm for Landsat/TM imagery basing on inverse distance spatial interpolation algorithm: A case study in Taihu Lake. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 882–889. [Google Scholar] [CrossRef]
- Wang, M.; Son, S.; Zhang, Y.; Shi, W. Remote sensing of water optical property for China’s inland Lake Taihu using the SWIR atmospheric correction with 1640 and 2130 nm bands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2505–2516. [Google Scholar] [CrossRef]
- Pahlevan, N.; Roger, J.-C.; Ahmad, Z. Revisiting short-wave-infrared (SWIR) bands for atmospheric correction in coastal waters. Opt. Express 2017, 25, 6015–6035. [Google Scholar] [CrossRef] [PubMed]
- Werdell, P.J.; Franz, B.A.; Bailey, S.W. Evaluation of shortwave infrared atmospheric correction for ocean color remote sensing of Chesapeake Bay. Remote Sens. Environ. 2010, 114, 2238–2247. [Google Scholar] [CrossRef]
- Adler-Golden, S.; Berk, A.; Bernstein, L.; Richtsmeier, S.; Acharya, P.; Matthew, M.; Anderson, G.; Allred, C.; Jeong, L.; Chetwynd, J. Flaash, a Modtran4 atmospheric correction package for hyperspectral data retrievals and simulations. In Proceedings of the 7th JPL Airborne Earth Science Workshop, Pasadena, CA, USA, 12–16 January 1998; JPL Publication: Pasadena, CA, USA, 1998; pp. 9–14. [Google Scholar]
- Brockmann, C.; Doerffer, R.; Peters, M.; Kerstin, S.; Embacher, S.; Ruescas, A. Evolution of the C2RCC neural network for Sentinel 2 and 3 for the retrieval of ocean colour products in normal and extreme optically complex waters. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; p. 54. [Google Scholar]
- Doron, M.; Bélanger, S.; Doxaran, D.; Babin, M. Spectral variations in the near-infrared ocean reflectance. Remote Sens. Environ. 2011, 115, 1617–1631. [Google Scholar] [CrossRef]
- Lamquin, N.; Bourg, L.; Lerebourg, C.; Martin-Lauzer, F.-R.; Kwiatkowska, E.; Dransfeld, S. System Vicarious Calibration of Sentinel-3 OLCI. 2017. Available online: https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-3-olci (accessed on 21 June 2018).
- Zibordi, G.; Mélin, F. An evaluation of marine regions relevant for ocean color system vicarious calibration. Remote Sens. Environ. 2017, 190, 122–136. [Google Scholar] [CrossRef] [PubMed]
- Canny, J. A computational approach to edge detection. In Readings in Computer Vision; Elsevier: Amsterdam, The Netherlands, 1987; pp. 184–203. [Google Scholar]
- McFeeters, S.K. The use of the Normalized Difference water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Shi, K.; Li, Y.; Li, L.; Lu, H. Absorption characteristics of optically complex inland waters: Implications for water optical classification. J. Geophys. Res. Biogeosci. 2013, 118, 860–874. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Feng, L.; Chen, X.; Yesou, H. Meris observations of chlorophyll-a dynamics in Erhai Lake between 2003 and 2009. Int. J. Remote Sens. 2014, 35, 8309–8322. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, S.; Liu, J.; Qian, X.; Ge, Y. Time-series modis image-based retrieval and distribution analysis of total suspended matter concentrations in Lake Taihu (China). Int. J. Environ. Res. Public Health 2010, 7, 3545–3560. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Shi, K.; Zhou, Y.; Liu, X.; Qin, B. Monitoring the river plume induced by heavy rainfall events in large, shallow, Lake Taihu using MODIS 250 m imagery. Remote Sens. Environ. 2016, 173, 109–121. [Google Scholar] [CrossRef]
- Bailey, S.W.; Werdell, P.J. A multi-sensor approach for the on-orbit validation of ocean color satellite data products. Remote Sens. Environ. 2006, 102, 12–23. [Google Scholar] [CrossRef]
- Goyens, C.; Jamet, C.; Schroeder, T. Evaluation of four atmospheric correction algorithms for MODIS-Aqua images over contrasted coastal waters. Remote Sens. Environ. 2013, 131, 63–75. [Google Scholar] [CrossRef]
- Mao, Z.; Chen, J.; Hao, Z.; Pan, D.; Tao, B.; Zhu, Q. A new approach to estimate the aerosol scattering ratios for the atmospheric correction of satellite remote sensing data in coastal regions. Remote Sens. Environ. 2013, 132, 186–194. [Google Scholar] [CrossRef]
- He, X.; Bai, Y.; Pan, D.; Huang, N.; Dong, X.; Chen, J.; Chen, C.-T.A.; Cui, Q. Using geostationary satellite ocean color data to map the diurnal dynamics of suspended particulate matter in coastal waters. Remote Sens. Environ. 2013, 133, 225–239. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, R.; Li, J.; Zhang, B.; Duan, H. A validation study of an improved SWIR iterative atmospheric correction algorithm for MODIS-Aqua measurements in Lake Taihu, China. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4686–4695. [Google Scholar] [CrossRef]
- Rotta, L.H.; Alcântara, E.H.; Watanabe, F.S.; Rodrigues, T.W.; Imai, N.N. Atmospheric correction assessment of SPOT-6 image and its influence on models to estimate water column transparency in tropical reservoir. Remote Sens. Appl. Soc. Environ. 2016, 4, 158–166. [Google Scholar] [CrossRef]
- Mobley, C.D. Hydrolight 4.0 Users Guide; Sequoia Scientific Inc.: Mercer Island, WA, USA; Bellevue, WA, USA, 1998. [Google Scholar]
- Kou, L.; Labrie, D.; Chylek, P. Refractive indices of water and ice in the 0.65-to 2.5-μm spectral range. Appl. Opt. 1993, 32, 3531–3540. [Google Scholar] [CrossRef] [PubMed]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Townshend, J.R.; Liang, S.; Kalluri, S.N.; DeFries, R.S. Impact of sensor’s point spread function on land cover characterization: Assessment and deconvolution. Remote Sens. Environ. 2002, 80, 203–212. [Google Scholar] [CrossRef]
- Meister, G.; Franz, B.; Turpie, K.; McClain, R. The MODIS Aqua point-spread function for ocean color bands. In Proceedings of the Ninth International Symposium on Physical Measurements and Signatures in Remote Sensing, Beijing, China, 17–19 October 2005; pp. 334–336. [Google Scholar]
- Jiang, L.; Wang, M. Identification of pixels with stray light and cloud shadow contaminations in the satellite ocean color data processing. Appl. Opt. 2013, 52, 6757–6770. [Google Scholar] [CrossRef] [PubMed]
- Hunt, S.; Nieke, J. A Radiometric Uncertainty Tool for OLCI. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; p. 420. [Google Scholar]
- Santer, R.; Schmechtig, C. Adjacency effects on water surfaces: Primary scattering approximation and sensitivity study. Appl. Opt. 2000, 39, 361–375. [Google Scholar] [CrossRef] [PubMed]
- Sterckx, S.; Knaeps, E.; Ruddick, K. Detection and correction of adjacency effects in hyperspectral airborne data of coastal and inland waters: The use of the near infrared similarity spectrum. Int. J. Remote Sens. 2011, 32, 6479–6505. [Google Scholar] [CrossRef]
- Sterckx, S.; Knaeps, S.; Kratzer, S.; Ruddick, K. Similarity Environment Correction (SIMEC) applied to MERIS data over inland and coastal waters. Remote Sens. Environ. 2015, 157, 96–110. [Google Scholar] [CrossRef]
- Qiu, S.; Godden, G.; Wang, X.; Guenther, B. Satellite-Earth remote sensor scatter effects on Earth scene radiometric accuracy. Metrologia 2000, 37, 411. [Google Scholar] [CrossRef]
- Doxaran, D.; Leymarie, E.; Nechad, B.; Dogliotti, A.; Ruddick, K.; Gernez, P.; Knaeps, E. Improved correction methods for field measurements of particulate light backscattering in turbid waters. Opt. Express 2016, 24, 3615–3637. [Google Scholar] [CrossRef] [PubMed]
- Amin, A.R.M.; Ahmad, F.; Abdullah, K. Discriminating sediment and clear water over coastal water using GD technique. Ekológia 2017, 36, 10–24. [Google Scholar] [CrossRef] [Green Version]
- Li, R.-R.; Kaufman, Y.J.; Gao, B.-C.; Davis, C.O. Remote sensing of suspended sediments and shallow coastal waters. IEEE Trans. Geosci. Remote Sens. 2003, 41, 559–566. [Google Scholar] [Green Version]
- Sun, L.; Wei, J.; Bilal, M.; Tian, X.; Jia, C.; Guo, Y.; Mi, X. Aerosol optical depth retrieval over bright areas using Landsat 8 OLI images. Remote Sens. 2015, 8, 23. [Google Scholar] [CrossRef]
- Bulgarelli, B.; Zibordi, G. On the detectability of adjacency effects in ocean color remote sensing of mid-latitude coastal environments by SeaWiFS, MODIS-A, MERIS, OLCI, OLI and MSI. Remote Sens. Environ. 2018, 209, 423–438. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.P. The impact of misregistration upon composited wide field of view satellite data and implications for change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2017–2032. [Google Scholar] [CrossRef]
- Sobrino, J.; Jiménez-Muñoz, J.; Sòria, G.; Ruescas, A.; Danne, O.; Brockmann, C.; Ghent, D.; Remedios, J.; North, P.; Merchant, C. Synergistic use of MERIS and AATSR as a proxy for estimating Land Surface Temperature from Sentinel-3 data. Remote Sens. Environ. 2016, 179, 149–161. [Google Scholar] [CrossRef]

















| Lakes | Lon. (°E) | Lat. (°N) | E(m) | TSM(mg/L) | Chla(μg/L) | SSD(m) | Reference |
|---|---|---|---|---|---|---|---|
| Lake Hongze * | 118.682 | 33.313 | 10 | 63.82 | 8.12 | 0.19 | This study |
| Lake Taihu * | 120.192 | 31.221 | 0 | 13.54 | 20.50 | 0.80 | This study |
| Lake Gehu * | 119.807 | 31.592 | 4 | 44.23 | 53.25 | 0.27 | [29] |
| Lake Poyang * | 116.216 | 29.180 | 10 | 49.88 | 10.42 | 0.65 | [29] |
| Lake Dianchi * | 102.701 | 24.824 | 1900 | 36.09 | 91.40 | 0.29 | This study |
| Lake Erhai | 100.190 | 25.785 | 1997 | 3.97 | 11.73 | 1.78 | This study |
| Lake Chenghai | 100.665 | 26.549 | 1506 | 7.80 | 0.72 | 1.6 | [41] |
| Lake Fuxian | 102.890 | 24.528 | 1920 | 1.24 | 1.56 | 5.57 | [28] |
| Lake Xingyun | 102.775 | 24.328 | 1888 | - | 14.5 | - | [44] |
| Lake Yangzonghai | 103.002 | 24.914 | 1930 | 2.07 | 1.10 | 2.40 | [41] |
| Lake Qinghai | 100.194 | 36.897 | 3200 | 2.28 | 0.857 | 3.18 | [40] |
| Lake Zhuhu | 116.150 | 29.134 | 13 | - | 7.76 | 1.00 | [43] |
| Region | Date (ISO8601) | Sensing Time (UTC) | In-Situ Number (n = 72) |
|---|---|---|---|
| Lake Taihu Lake Gehu | 24 July 2017 | 01:50 | 35 |
| 24 July 2017 | 01:53 | ||
| Lake Hongze | 7 December 2016 | 02:27 | 8 |
| 8 December 2016 | 02:01 | 8 | |
| 18 May 2017 | 02:27 | 7 | |
| Lake Erhai Lake Chenghai | 19 April 2017 | 03:23 | 14 |
| Lake Dianchi Lake Fuxian Lake Yangzonghai Lake Xingyun | 14 November 2017 | 03:01 | - |
| Lake Qinghai | 12 July 2017 | 03:39 | - |
| Lake Poyang Lake Zhuhu | 31 October 2017 | 02:24 | - |
| Index | Combinations | Lake Erhai | Lake HongzeW | Lake HongzeS | Lake Taihu |
|---|---|---|---|---|---|
| MAPE (%) | OL16 + OL17 | 160.02 | 58.11 | 59.91 | 56.19 |
| OL16 + SL05 | 61.18 | 49.45 | 61.04 | 53.54 | |
| OL17 + SL05 | 40.05 | 43.24 | 54.91 | 50.17 | |
| OL21 + SL05 | 65.78 | 40.84 | 45.80 | 64.52 | |
| OL21 + SL06 | 53.09 | 31.70 | 37.33 | 45.17 | |
| SL05 + SL06 | 60.41 | 17.10 | 19.95 | 32.96 | |
| MRPE (%) | OL16 + OL17 | −143.87 | −58.11 | −31.44 | −53.90 |
| OL16 + SL05 | 54.69 | −49.45 | 60.26 | −51.63 | |
| OL17 + SL05 | 28.43 | −43.24 | 53.75 | −47.85 | |
| OL21 + SL05 | −60.99 | −40.84 | 34.22 | −63.58 | |
| OL21 + SL06 | −44.35 | −31.48 | 13.01 | −42.98 | |
| SL05 + SL06 | −49.98 | −5.57 | 7.77 | 18.39 | |
| RMSE (sr−1) | OL16 + OL17 | 0.00202 | 0.00772 | 0.00362 | 0.00602 |
| OL16 + SL05 | 0.00056 | 0.00667 | 0.00267 | 0.00569 | |
| OL17 + SL05 | 0.00045 | 0.00604 | 0.00239 | 0.00542 | |
| OL21 + SL05 | 0.00060 | 0.00578 | 0.00180 | 0.00658 | |
| OL21 + SL06 | 0.00052 | 0.00476 | 0.00174 | 0.00486 | |
| SL05 + SL06 | 0.00054 | 0.00267 | 0.00134 | 0.00251 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, S.; Li, Y.; Wang, Q.; Lyu, H.; Liu, G.; Zheng, Z.; Du, C.; Mu, M.; Xu, J.; Lei, S.; et al. Inland Water Atmospheric Correction Based on Turbidity Classification Using OLCI and SLSTR Synergistic Observations. Remote Sens. 2018, 10, 1002. https://doi.org/10.3390/rs10071002
Bi S, Li Y, Wang Q, Lyu H, Liu G, Zheng Z, Du C, Mu M, Xu J, Lei S, et al. Inland Water Atmospheric Correction Based on Turbidity Classification Using OLCI and SLSTR Synergistic Observations. Remote Sensing. 2018; 10(7):1002. https://doi.org/10.3390/rs10071002
Chicago/Turabian StyleBi, Shun, Yunmei Li, Qiao Wang, Heng Lyu, Ge Liu, Zhubin Zheng, Chenggong Du, Meng Mu, Jie Xu, Shaohua Lei, and et al. 2018. "Inland Water Atmospheric Correction Based on Turbidity Classification Using OLCI and SLSTR Synergistic Observations" Remote Sensing 10, no. 7: 1002. https://doi.org/10.3390/rs10071002
APA StyleBi, S., Li, Y., Wang, Q., Lyu, H., Liu, G., Zheng, Z., Du, C., Mu, M., Xu, J., Lei, S., & Miao, S. (2018). Inland Water Atmospheric Correction Based on Turbidity Classification Using OLCI and SLSTR Synergistic Observations. Remote Sensing, 10(7), 1002. https://doi.org/10.3390/rs10071002