Next Article in Journal
A Preprocessing Method for Hyperspectral Target Detection Based on Tensor Principal Component Analysis
Next Article in Special Issue
Pléiades Tri-Stereo Data for Glacier Investigations—Examples from the European Alps and the Khumbu Himal
Previous Article in Journal
Soil Moisture from Fusion of Scatterometer and SAR: Closing the Scale Gap with Temporal Filtering
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 10
Issue 7
10.3390/rs10071031
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Annual Glacier-Wide Mass Balance (2000–2016) of the Interior Tibetan Plateau Reconstructed from MODIS Albedo Products

by
Zhimin Zhang
1,2,
Liming Jiang
1,2,*,
Lin Liu
1,3,
Yafei Sun
4 and
Hansheng Wang
1
1
State Key Laboratory of Geodesy and Earth’s Dynamics, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 340 XuDong Rd, Wuhan 430077, China
2
University of Chinese Academy of Sciences, 19A Yuquan Rd., Beijing 100049, China
3
School of Physics, Huazhong University of Science and Technology, 1037 LuoYu Rd., Wuhan 430074, China
4
School of Surveying and Urban Spatial Information, Henan University of Urban Construction, LongXiang Rd., Pingdingshan 467036, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2018, 10(7), 1031; https://doi.org/10.3390/rs10071031
Submission received: 18 April 2018 / Revised: 8 June 2018 / Accepted: 28 June 2018 / Published: 30 June 2018
(This article belongs to the Special Issue Remote Sensing of Glaciers at Global and Regional Scales)
Browse Figures
Versions Notes

Abstract

:
Glaciers in the Tibetan Plateau (TP) play a crucial role in regulating agriculture irrigation, river discharge and the regional/global climate system. However, mass balance records of TP glaciers have remained scarce due to challenging mountainous terrain and harsh weather conditions, which limits our understanding of the influence of melting glaciers on local water resources and responses to climate change. Here, we present and assess an albedo-based method to derive annual mass balance for three glaciers in the interior TP from Moderate Resolution Imaging Spectroradiometer (MODIS) albedo data during 2000–2016. A strong linear correlation (R2 = 0.941, P < 0.001) is found between annual minimum-averaged glacier-wide albedo (AMGA) values and annual mass balance measurements on the Xiao Dongkemadi glacier. Furthermore, the 17-year-long annual mass balance series of the Xiao Dongkemadi glacier and the Geladandong mountain region glaciers, and the Purogangri ice cap are reconstructed for the first time, with a mass loss rate of 535 ± 63 mm w.e.a−1, 243 ± 66 mm w.e.a−1 and 113 ± 68 mm w.e.a−1, respectively. The results are verified by geodetic estimates, with relative error ranging from 4.55% to 11.80%, confirming that the albedo-based method can be used to estimate specific mass budgets for interior TP glaciers. A strong correlation between the mass balance series and air temperature infers that increasing summer air temperature may be one of main reasons for glacier shrinkage of the three studied glaciers.

Graphical Abstract

1. Introduction

The Tibetan Plateau (TP), which is home to the largest number of glaciers outside the polar regions, is characterized by very high warming rates, up to 0.29~0.50 °C/10 years, twice as high as the average global warming rate [1]. These glaciers are mostly located at the headwaters of large Asian rivers such as the Yangtze, Mekong, Brahmaputra, and Indus Rivers, providing a valuable water supply in the form of meltwater for millions of people for drinking, agriculture, and manufacturing [2,3,4,5]. However, field glaciological observations (particularly mass balance (MB) measurements) in the TP remain scarce, due to challenging mountainous terrain and harsh weather conditions [6,7,8]. There are only 15 glaciers with intensive in situ measurements of mass balance [9], which is less than 0.05% of 36,800 glaciers over this region [10]. The incomplete knowledge of glacier mass balance over the TP limits our understanding of glacier variations and their response to climate changes at the regional or global scale.
In recent years, remote sensing techniques have proven to be useful for glacier monitoring, since the available satellite sensors are increasing and their spatial, radiometric and temporal resolutions are improved [11,12].Glacier mass fluctuations can be calculated by using several parameters derived from remote sensing images, e.g., the difference between two digital elevation models (DEMs) at different times [13,14,15,16], the equilibrium–line altitude (ELA) at the end of the hydrological year [12,17,18], the accumulation–area ratio (AAR) [19,20] over a glacier, and the average glacier surface albedo [21,22,23,24]. Among these glacier properties, recent studies have revealed that the variation of glacier-wide surface albedo has shown outstanding potentials in obtaining annual or seasonal mass balance, because minimum surface albedo was directly related to AAR and ELA. Dumont et al. [22] concluded that a strong linear correlation exits between minimum Moderate Resolution Imaging Spectroradiometer (MODIS)-derived albedo value and glacier mass balance, which could be used to retrieve inter-annual variations of glacier mass balance. Sirguey et al. [23] confirmed that minimum glacier-wide albedo was a reliable predictor for annual mass variability in a maritime glacier and reconstructed both winter and summer balance records. Recently, based on a methodological framework proposed by Sirguey et al. [23], the albedo-based method was exploited to quantify annual and summer mass balance on 30 glaciers in the French Alps [24]. In addition, Brun et al. [21] assessed this albedo-based method to reconstruct the glacier mass balance for summer accumulation-type and winter accumulation-type glaciers in the Himalayas from MODIS surface albedo data and discussed the prospects of using spatial extrapolation of the established regression models for unmonitored neighboring glaciers that have similar climatological conditions to the studied glaciers [21].
The main objectives of this study were to assess the applicability of the albedo-based method to continental glaciers in the interior TP and reconstructed the annual mass balance for three glaciated regions, Xiao Dongkemadi (XD) glacier, Purogangri ice cap (PIC) and Geladandong mountain region (‘GLDD’) glaciers, derived from the MODIS albedo data. Specifically, the glacier surface albedo was retrieved from MODIS daily albedo products between 2000 and 2016. In addition, the annual minimum-averaged glacier-wide albedo (AMGA) was utilized to build a linear regression model with in situ mass balance records on the XD glacier. We also attempted to spatially extrapolate the albedo-MB regression model to climatologically similar glaciated regions close to the XD glacier, the GLDD glaciers, and the PIC. As a result, the annual mass budgets of the two regions since 2000 were reconstructed and verified with geodetic estimates. Finally, the influence of local climate indicators (air temperature and precipitation) on glacier mass changes was analyzed, and the potential and limitations of the method were discussed.

2. Site Description

2.1. Geological and Glaciological Settings of the Study Area

The study area is in the interior TP with a mean elevation more than 5000 m a.s.l., close to the Yangtze River source region (YRSR), which is an important source of fresh water for the local native people and alpine wildlife [25,26,27]. The interior TP is primarily dominated by continental/subcontinental climate conditions and is less influenced by the mid-latitude westerlies and the Indian monsoon system than other regions in high mountain Asia (e.g., the Pamir–Karakoram–Himalaya) [9]. This continental climate-dominated region is characterized by an extremely dry and cold climate due to the limited water vapor source from the westerlies and Indian monsoons, leading to sparse glacier distributions and high equilibrium-line altitudes (ELAs) above 5600 m a.s.l. [9]. Overall, the total annual precipitation in the interior TP is less than 500 mm, around 60–70% of which is in the summer months. Meteorological data at Tuotuohe (34°13′ N, 92°26′ E, about 130 km from the Dongkemadi glacier) indicate that the mean annual air temperature is approximately −2.7 °C, and the highest monthly average temperatures (>0 °C) occurred during June–September.
Three representative continental-type [28] glaciated regions (see Figure 1) were selected in this study: the XD, PIC, and GLDD glaciers, because they are affected by the same dry and cold continental climate and have similar conditions of little annual precipitation (~300 mm) and low air temperature (~−9 °C), see Table 1. About 30% of the annual precipitation occurs in the winter season, while most (over 60%) of the precipitation falls in the summer. In addition, the three glaciated regions are located close to each other, with a distance from the GLDD to Dongkemadi and PIC of about 90 and 200 km, respectively.
The XD glacier, a tributary of the Dongkemadi glacier, located at the headwaters of the Dongkemadi River, covers an area of 1.77 km2 and has an ELA close to 5620 m a.s.l. [29]. We choose the XD glacier in our study because the in situ annual mass balance is measured at this tributary glacier. Besides the XD glacier, the Dongkemadi glacier has a trunk glacier named Da (Greater) Dongkemadi (DD), covering an area of 14.63 km2, with an ELA of 5600 m a.s.l. [30]. The PIC, located in the western part of the Tanggula Mountains, is Tibet’s largest modern ice field with a glaciered area of over 420 km2 [31]. It is composed of more than 50 glaciers of variable lengths radiating from the center to the piedmont terminus [32]. The altitude of the PIC ranges from 5350 to 6370 m a.s.l. [33] with a mean ELA of 5748 m a.s.l. [34]. Serving as headwaters of the Yangtze River, the glaciers in GLDD consist of two major parts: the western and eastern parts (see Figure 1). The western part covers a glaciered area of 185 km2 and the eastern covers an area about 600 km2. The mean ELA over the GLDD is 5740 m a.s.l., with an elevation between 5200 and 6621 m a.s.l. [35]. Table 1 lists the topographical and climatic characteristics of the studied glaciers.

2.2. Previous Studies

In situ observations suggested that the XD glacier had experienced various mass changes during the past decades [9]. The cumulative mass gain between 1989 and 1993 was 970 mm w.e., whereas the cumulative mass loss (−3103 mm w.e.) was found in the years from 1994 to 2002. Meanwhile, glacier retreat accelerated since 2000 due to the increase of summer air temperature and decrease of surface albedo [36]. Recent studies showed that total glacier surface elevation decreased by about 1.76 m from 2008 to 2012. The average ELA was 5720 m in this period, which was 120 m higher than that in the early 1990s [37].
The PIC, which experienced a slight terminus retreat, has a relatively stable status compared with other glaciers in the TP. In the western part of the PIC, glacier No. 5Z611A6 retreated by 20 m from post Little Ice Age to the 1970s, and by 40~50 m in the later 20 years [38]. Moreover, the rate of glacier thickness change varied in the past decades. Studies have reported that total mean surface thickness at the PIC decreased by 6.19 ± 1.91 m (0.24 ± 0.07 m/a) between 1974 and 2000 [39]. Meanwhile, annual surface thinning ranged from 0.049 m/a [8] to 0.317 m/a [40] for the periods 2000–2012 and 2012–2016.
In recent years, continuously increasing summer air temperature has been the major reason for the shrinkage of the GLDD glaciers [35,41]. From 1973 to 2009, these glaciers experienced a shrinkage in area cover, with an average rate of decrease of about 2.65 km2/a [42], and glacier shrinkage is still on-going [35]. Besides, glacier variation appeared to have heterogeneous spatial characteristics, meaning some glaciers advanced but others retreated [41], and the glacier tongues on the eastern side of the mountain tended to melt more seriously than those on the western side [35].

3. Datasets

3.1. Observations of Glacier Mass Balance

Given the advantage of the natural conditions of a gentle surface without any avalanches or surface moraines, mass balance of the XD glacier has been measured by the stake method since 1989, providing the longest data series over the TP [43]. Twenty-five stakes were set up on the glacier surface at sites ranging in elevation from 5400 to 5750 m a.s.l., which covers both the accumulation and ablation zones. Four snow pits were set up in the glacier accumulation zone, with an elevation between 5700 and 5800 m a.s.l. [43]. The measurement records at each site include the stake height over the glacier surface, firn layer thickness and density, thickness of superimposed ice, and structure of snow pit profiles. They were obtained by manual observation in the ablation season every year, which generally begin in late May or early June and end in late September or early October [37]. Net ablation was measured by the stakes’ heights and the firn pits in the ablation area, and net accumulation was measured by the snow pits in the accumulation zone [43]. In this study, we used the in situ measurements of annual mass balance between 2002 and 2010 from the published paper [9], which provide an ideal source for calibration and validation of the linear correlation model between AMGA and mass budgets.
In addition, the mean geodetic mass balances for the XD and GLDD glaciers [40,44] were also used for verification of the mass balance results estimated by the albedo-based method. The mean geodetic mass balances were calculated with the DEM differencing method [45].

3.2. MODIS Albedo Products

Williamson et al. [46] compared the field measured albedo to the daily Moderate Resolution Imaging Spectroradiometer (MODIS) snow albedo product on glaciated surfaces and found a high correlation between black-sky albedo products and field measurements. In this study, the MODIS daily snow cover product of MOD10A1/MYD10A1 (tile: h25v05) onboard the Terra/Aqua platform was employed for albedo estimation. The MODIS data products at 500 m pixel resolution, delivered by the National Snow and Ice Data Center (NSIDC), consists of daily snow cover, daily snow albedo (DSA), fractional snow cover, and snow spatial quality assessment (QA). The DSA products provide the black-sky (or broadband) albedo for the areas that are classified as snow cover and have cloud-free coverage identified by the MODIS cloud-mask product [47]. In addition, the daily snow albedo data is generated when the viewing and illumination angles are at the best conditions in a day [48].
The DSA products from MOD10A1 during the period 2000 to 2016 and MYD10A1 from 2002 to 2016 were used in this study. To calculate the minimum average albedo over a glacier, the albedo products during the ablation season from June 1 to September 30 were selected. However, the MOD10A1 DSA data of 19 June 2000, 7–19 August 2000, and 15 June to 2 July in 2001, were absent. There was 11.48% absent data in 2000 and 14.75% in 2001. Ultimately, there were about 244 images for snow albedo processing every year. It should be noted that the XD glacier only covers 5 pixels in the MODIS albedo products, so it is scarcely possible to grasp the variations of glacier-wide albedo from such little data coverage. Furthermore, the Landsat-derived albedo results show that the mean value of glacier-wide albedo at the Dongkemadi glacier is almost identical to that of the XD glacier, with an absolute difference of less than 1% (see Supplementary Table S1). Therefore, we utilized the glacier-wide albedo at Dongkemadi glacier (60 pixels in the DSA product) as a substitute for the XD glacier and neglected the error derived from their difference. The area covered by the MODIS DSA pixels is 15 km2, which is slightly smaller than the actual area coverage of 16.4 km2 in the Dongkemadi glacier. The following regression analysis was made by using the glacier-wide albedo and in situ mass balance at the XD glacier in this study. The total number of DSA pixels for the PIC and GLDD was 1557 and 3087, respectively. The method of AMGA calculation will be presented in Section 4.1.

3.3. Climate Datasets

The High Asia Refined analysis (HAR; Maussion et al., 2014) data provided by the chair of climatology at the Technical University of Berlin was employed to evaluate the influence of climate changes on glacier mass budgets. It was generated with the advanced research version of the Weather Research and Forecasting model (WRF–AEW version 3.3.1), which was forced with the Operational Model Global Tropospheric Analyses (Final Analyses (FNL); dataset ds083.2) [49]. The data comprises two datasets of 30 km and 10 km resolution, including pressure, geopotential height, temperature, and wind direction and speed. This re-analysis product with a 10 km spatial resolution has been widely used for various geo-biophysical applications in climatic, hydrological, and glaciological studies [49,50,51] and can be accessed for free at http://www.klima.tu-berlin.de/HAR.
We chose the monthly HAR data during the period 2001 to 2013 and only the grid points within or near the glacier outlines (see Figure 1) were considered. The air temperature at 2-m above the ground (t2; °C) and the total precipitation (prcp; mm) were analyzed. Owing to the overestimate of the HAR precipitation [49], following the method of Mölg et al. [51], we applied a scaling factor to calibrate the precipitation in the studied regions. Specifically, field annual precipitation from the automatic meteorological station at XD glacier is 302 mm [43], while the annual precipitation from the HAR grids is 730 mm. Therefore, a scaling factor of 0.41, which is the ratio of 302 to 730, was applied for the HAR precipitation calibration. In addition, this scaling factor was also calibrated on HAR precipitation amounts at the PIC and GLDD. All the data utilized in this study were summed in Table 2.

4. Method

In this study, an albedo-MB regression model was constructed with the annual minimum-averaged glacier-wide albedo (AMGA) and in situ mass balance record at the XD glacier. AMGA was calculated from the MODIS daily albedo products. Further, annual mass balance series (2000–2016) in the three glaciated regions were reconstructed, in addition to the results comparison and validation. Figure 2 illustrated the flowchart of the data processing and result analysis.

4.1. Estimation of Glacier-Wide Albedo from MODIS Products

Cloud cover is one of the major influence factors in the glacier-wide albedo estimation. In this study, the snow albedo values (in the range of 0–100) in the DSA product were considered, and other non-snow albedo values, such as cloud (150), were set to null and not included in the data processing. To weaken the effect caused by the cloud cover, we merged the daily MOD10A1 and MYD10A1 DSA data into one scene of MO&YD10A1 image and utilized a mean filter of 10 temporal samples to calculate the average glacier-wide albedo.
Prior to data merging and filtering, data preprocessing should be carried out before the glacier-wide albedo estimation. The MODIS Reprojection Tool (release 4.1, 2011), a recommended software supporting higher-level MODIS land products (https://lpdaac.usgs.gov/tools/modis_reprojection_tool), was used in the data preprocessing for MOD10A1 and MYD10A1 products, including map re-projection, format conversion, and spatial sub-setting. To ensure uniformity in the validation results with the geodetic method, we re-projected the MODIS products from the sinusoidal projection into the Universal Transverse Mercator (UTM) projection with the datum of WGS84. Then, these MODIS products were extracted by glaciered areas that were extracted according to the second Chinese glacier inventory.
The MOD10A1 and MYD10A1 DSA products were obtained from different platforms, at different data acquisition times, and with different weather conditions, which led to the result that the albedo values in the daily MOD10A1 and MYD10A1 were not identical even at the same site. Therefore, we merged the daily MOD10A1 and MYD10A1 DSA data into one scene of MO&YD10A1 image per day to improve the efficiency of data utilization. Data merging was achieved by the following guidelines: (1) if pixels were identified as snow cover in only MOD10A1 or MYD10A1, their corresponding values were considered in the MO&YD10A1 image; (2) when both MOD10A1 and MYD10A1 were cloud-free for a pixel, their average value was employed in the MO&YD10A1 image; and 3) otherwise, the pixels were classified as cloud and neglected in subsequent processing steps. As a result, after data merging, the effective data coverage in the MO&YD10A1 image was increased by 14.2%, 16.4% and 16.2% for the XD, PIC, and GLDD glaciers, respectively, in comparison to the MOD10A1.
A mean filter in time was employed in the merged MO&YD10A1 time series to further reduce the influence of cloud cover and improve the signal-to-noise ratio. We calculated the average glacier-wide albedo series ( α d 10 ¯ ) by a 10-day moving window (10 temporal samples) every day for the MO&YD10A1 daily albedo series. Consequently, α d 10 ¯ in the summer (June to September) were obtained by averaging the filtered MO&YD10A1 data across the entire glacier, from which the AMGA could be determined for the 3 glaciered areas.

4.2. Construction of the Aass Balance Model

An albedo-MB regression model can be constructed based on the linear relationship between measured annual mass balance and annual minimum-averaged glacier-wide albedo (AMGA) as:
M B = A ∗ α d 10 ¯ min + B
where A and B are slope and intercept of the regression model, and α d 10 ¯ min indicates the AMGA retrieved from MODIS daily albedo products.
The constructed albedo-MB regression model between the MODIS-derived AMGA and the in situ mass balance for the XD glacier is presented in Figure 3. In the linear model, the annual mass balances during 2002–2010 were selected, as both MOD10A1 and MYD10A1 products are available for this period. The regression coefficients, Pearson’s correlation coefficient (R), and regression line were all calculated, following the method reported in York et al. [52].
Due to the inadequate datasets in the model construction, it is difficult to use one series for calibration and others for validation. Therefore, we applied the leave-one-out cross-validation (LOOCV) technique [53] for the sensitivity analysis of the albedo-MB regression model. Specifically, for each year (j) from 2002 to 2010, we used the observed mass balance and AMGA to construct a model for the mass balance calculation (LOOCV mass balance) and used the selected year as a single-item test (mass balance in the j year). In this way, the dependence between the calibration and validation datasets could be avoided and we could ensure independence between the data we used to estimate mass balance and the data we used to assess the corresponding estimation error. Table 3 shows the results of the LOOCV for the albedo-MB regression model. Analysis indicates that there is small variability (mean ± standard deviation) in the regression parameters of A and B, which is 4385.44 ± 230.51 and −2338.52 ± 99.06. The mean difference between the in situ mass balance and the LOOCV value is −5.40 mm w.e., and the standard deviation of the difference can be considered as the model error in the mass balance estimation. The significant and strong correlation (R2 = 0.941, P < 0.001) also suggests that AMGA is a reliable indicator of glacier change and can be used in the subsequent analysis.

4.3. Uncertainty Analysis

The error variances of the estimated mass balance contained three separate error sources. The first was the estimation error of the parameter A ( σ A ) and the second was the estimation error of the parameter B ( σ B ). They were calculated by the method reported in York et al. [52]. The third error source was the error of the AMGA ( σ α d 10 ¯ min ), which was related to the accuracy of the MO&YD10A1 albedo and the pixel number within the glacier. Many researchers have made accuracy assessments of MODIS daily albedo products with in situ measurements. Comparison with in situ albedo measurements collected in Greenland indicated that the overall root mean square error (RMSE) was 0.067 and 0.075 for the MOD10A1 and MYD10A1 daily albedo products, respectively [54]. Ground-based albedo observation made in Karasu basin, Turkey, showed that error of the MODIS albedo values were within 10% of the in situ values [55]. Wu et al. [56] took the field albedo observation at Dongkemadi glacier on May 11, 2011, and found that the field albedo was 0.638, which was 0.046 bigger than that in the MOD10A1 products. Hence, we used 10% of the annual maximum MO&YD10A1 values as the MO&YD10A1 albedo errors according to these previous studies. Using the method proposed in [22,23], σ α d 10 ¯ min was computed as the MO&YD10A1 error divided by the root mean square of the number of glacier pixels. Based on the propagation law [57], the error variance of the estimated mass balance could be written as:
σ M B 2 = ( ∂ M B ∂ A ) 2 σ A 2 + ( ∂ M B ∂ α d 10 ¯ min ) 2 σ α d 10 ¯ min 2 + σ B 2
Ultimately, the overall uncertainties of the derived mass balance for the XD glacier during 2000–2016 ranged from 226 mm w.e. to 299 mm w.e., with a mean value of 257 mm w.e.a−1. For PIC and GLDD, the mass balance uncertainties during 2000–2016 ranged from 248 mm w.e. to 305 mm w.e. and 233 mm w.e. to 299 mm w.e., with a mean value of 280 mm w.e.a−1 and 271 mm w.e.a−1, respectively. These were comparable with the errors reported by Burn et al. (100–190 mm w.e.a−1) [21] and Sirguey et al. (520–590 mm w.e.a−1) [23].

5. Results

5.1. Variations of the MODIS-Derived Glacier-Wide Albedo

Spatiotemporal variations of the derived glacier-wide albedo after the 10-day moving average are illustrated in Figure 4, in which the voids mean missing data. A clear evolution trend of the glacier surface albedo in the ablation season is obtained over the studied glaciers. In addition, the three glaciated regions experience a similar temporal pattern of glacier-wide albedo variation during the ablation season. Generally, larger values of albedo (yellow) occur in both the beginning and end of the ablation season, while smaller ones (blue) occur in the middle of this season. Most of the glacier-wide albedo reaches its minimum during the main melt season of mid-July and mid-August, possibly suggesting quick ice melt in this period. Figure 5 showed the annual minimum-averaged glacier-wide albedo (AMGA) from 2000 to 2016 for the three studied glaciated regions. We find that variations of AMGA are relatively stable from 2000 to 2006, but the variations are much larger in the next 11 years. This indicates that glacier mass balance is more fluctuant after 2006 in the glaciers of interior TP.
Further, the three glaciered areas have variable behavior of albedo distribution, as shown in Figure 4. A heterogeneous albedo pattern is found in the XD glacier, with the biggest temporal variation of glacier-wide albedo; however, the PIC and GLDD glaciers behave in a similar pattern of relatively low and homogeneous albedo variation. Standard deviation (see Supplementary Figure S1) of the glacier-wide albedo over the three studied regions also suggests that the mean value at the XD glacier is a little bigger than that in the PIC and GLDD. Moreover, Figure 5 illustrates that the AMGA in the XD glacier is slightly smaller than that in the other two regions. XD is characterized by lower values and highest variability, also due to its smaller size compared to the PIC and GLDD. Such diverse distribution and magnitude of glacier-wide albedo over the three glaciers result in different annual glacier mass balance, as described in Section 6.1.

5.2. Reconstructed Annual Mass Balance Series

Seventeen years (2000–2016) of annual mass balance of the XD glacier have been obtained by employing the albedo-MB regression model and the time series of albedo products (see Supplementary Table S2). Figure 6a illustrates a comparison between the mass balance series observed (blue points) and reconstructed (black points) at the XD glacier. Result of the LOOCV (see Table 3) indicates that the error of the albedo-MB regression model is 134.17 mm w.e., which suggests that the model can be used for robust mass balance estimation. Significant negative mass balance series are predicted in all six extended years (2011 to 2016), suggesting continuously rapid shrinkage of the XD glacier since 2000, which coincides with the decreasing size and thickness in this region [58]. Please note that the difference between in situ and reconstructed mass budget is 379 mm w.e. in 2000. This is because the glacier is seriously covered by clouds on the days when the minimum albedo is calculated, especially in the accumulation zone. Therefore, the calculated AMGA is dominated by the albedo result of the ablation zone, thereby resulting in an underestimation of the mass balance this year. Consequently, we consider the reconstructed annual mass balance after 2002 for subsequent analysis.
The albedo-MB regression model for the XD glacier was extended to the nearby glaciated regions of the PIC and GLDD glaciers and their annual mass balance were reconstructed. Figure 6b,c shows the 17-year-long annual mass balance records over PIC and GLDD. Generally, the annual mass balance series of these three regions have a similar changing trend during the studied period, with three dominantly positive sequences in 2005, 2008, and 2011, subsequently interrupted by three negative glacier balance records in 2006, 2010, and 2013. A comparison of the average annual mass balance derived from the albedo-based method and the geodetic method (red lines in Figure 6b,c) suggests that the reconstructed mass balance is reliable for the neighboring glaciers in this study.
The MODIS-derived annual mass balance series in Figure 6 suggest that the three glaciated regions experienced definite glacier mass loss over the period 2000–2016, and the glacier mass loss accelerated since 2012. The maximum glacier mass wastage with a loss rate of 535 ± 63 mm w.e.a−1 is found at the XD glacier, approximately double and four times that over the GLDD (243 ± 66 mm w.e.a−1) and the PIC (113 ± 68 mm w.e.a−1).

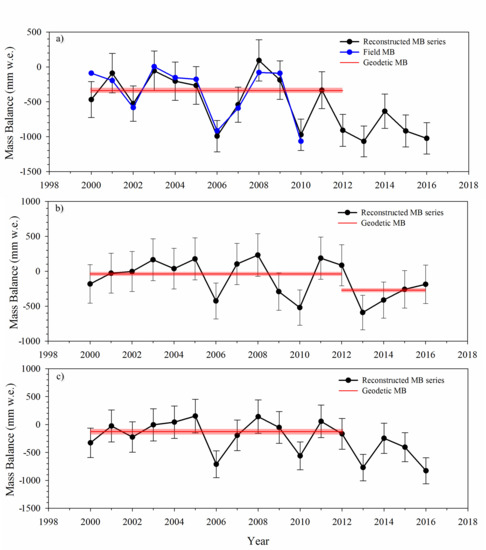
5.3. Comparison with Glacier Mass Balance and ELA Estimates

Table 4 summarizes the specific mass balance estimates for the three regions from previously published studies and this study. The data used in the geodetic method were acquired in the first half year, such as January 2012 and January 2016. The MODIS-derived annual mass balance corresponded to the hydrologic year mass balance. Thus, we chose the mass balance values in the period that was consistent with the geodetic results. Overall, the albedo-based mass balance results agree well with the glaciological, geodetic, and physical model-based estimates, although with relatively larger uncertainties compared with geodetic mass balance estimates. The physical model-based method is a multilayer subsurface snow and ice model that is used to calculate the surface energy-balance (SEB) and mass balance [33].
For the XD glacier, the average mass loss during 2000–2010 shows strong consistency between our result (383 ± 81 mm w.e.a−1) and the previous glaciological result (358 mm w.e.a−1) reported by Yao et al. [9]. The MODIS-derived mass loss rate in our study is 379 ± 77 mm w.e.a−1 from 2000 to 2012, whereas the value from the geodetic method is 339 ± 37 mm w.e.a−1 in the same period, leading to a relative error of 11.80%. The temporal coverage of the geodetic measurements is from February 2000 to February 2012, whereas the MODIS-derived mass balance result is between 2000 and 2011. Hence, the slightly different in the data period might contribute to the higher relative error.
The mean geodetic mass balance over the PIC exhibits great variability during the two studied periods, in which mass loss significantly increases from 44 ± 15 mm w.e.a−1 during 2000–2012 [8] to 269 ± 25 mm w.e.a−1 during 2012–2016 [40]. Similar results are obtained by our albedo-based method, with a relative error less than 10%, and the mass loss rates of 46 ± 82 mm w.e.a−1 and 294 ± 134 mm w.e.a−1 for the two periods. Moreover, the MODIS-derived mass budget of 2000–2012 is also comparable with the physical model-based result by Huintjes et al. [33], despite larger uncertainties.
For the GLDD, the average glacier mass loss rate based on interferometry is 128 ± 49 mm w.e.a−1 from 2000 to 2012, which is in good agreement with the MODIS-derived mass loss of 143 ± 80 mm w.e.a−1. By using the ICESat observations, Chao et al. [59] discovered that the GLDD glaciers were continuously melting, with a rate of mass change of 134 ± 56 mm w.e.a−1 for the period 2003–2009, which is slightly smaller than our result of 104 ± 115 mm w.e.a−1. This can probably be attributed to the fact that ice footprints of the ICESat are mostly over the ablation zone. However, in the periods 2000–2014 and 2000–2015, the average glacier thinning of the albedo-based method is 193 ± 71 mm w.e.a−1 and 207 ± 69 mm w.e.a−1, respectively, slightly different from the geodetic results reported by Liu et al. [60] and Chen et al. [61]. This difference might be due to the different temporal and spatial coverage of the studied GLDD glaciers for the two epochs (see Table 4).
In addition, we also calculated the annual mass balance series over the West and East GLDD (see Figure 1) and compared the respective results to the geodetic mass balance. The MODIS-derived mass loss rate in the East GLDD region is 146 ± 80 mm w.e.a−1 during 2000–2011, which agrees with that in the geodetic method of 155 ± 48 mm w.e.a−1. In the West GLDD, the average mass loss rate (202 ± 79 mm w.e.a−1) from our albedo-based method, although falls in between the results from Chen et al. [59] and Liu et al. [61], is smaller than the mean value of Liu [44] (89 ± 48 mm w.e.a−1). This is probably attributed to the influence of two surge glaciers [61], whose surface is generally heavily debris-covered [62]. It may lead to the lower glacier-wide albedo and much negative mass balance in this region. Due to the complex surge mechanism, the correlation between the variation of albedo and mass balance is unclear. Therefore, an intensive study of the relationship between glacier surging and albedo change should be need for the surge glaciers.
As an important parameter in characterizing the state of a glacier, ELA where the net mass balance is zero is a useful proxy for inter-annual mass balance variation [63]. The location of the ELA that can be interpreted as the response to climate change varies with the evolution of a glacier: the more positive the net mass balance, the lower the ELA, and vice versa. Therefore, we compared the time series results between our MODIS-derived mass balance and ELAs at the XD glacier and the PIC (Figure 7). The ELAs at the XD glacier were obtained from the Landsat imagery following the method of Rabatel et al. [12], and the ELAs at the PIC were derived from the MODIS data by Spieß et al. [34] at the end of the ablation season. Generally, there is an opposite inter-annual relationship between glacier mass balances and ELAs in both studied areas. In addition, the ascending or descending amplitude is also generally consistent, which coincides with the glacier evolutionary rules. This indicates that the derived mass balance from the albedo-based method is reliable. However, there is an exception at the PIC in the period 2001 to 2002, in which the mass balance increased from −28 mm w.e. to −4 mm w.e., and the ELA rose by 11 m simultaneously. This might be attributed to the deficiency of AMGA in these two years (see Section 5.2) and the uncertainty of ~20 m in the ELA estimation [34].

5.4. Linkage to Local Climate Variables

Air temperature and precipitation are two key climatic indicators, related to glacier melt and accumulation respectively [64,65]. To evaluate the dependence of glacier mass balance on local climate variables (annual precipitation, summer precipitation, annual air temperature, and summer air temperature), we employed simple linear regression (SLR) analysis to examine their relationships by calculating their correlation coefficients (R) and the significance level (P). The SLR analysis tool in the Statistical Product and Service Solutions (SPSS) version 20.0 software package was utilized in this study.
Figure 8 illustrates the correlations between the local climate indicators and annual glacier mass balance values for the three studied areas. Overall, summer and annual precipitation are not significant controls (P > 0.05; Figure 8a,b,e,f,i,j) on mass balance over the three glaciated regions. A possible explanation is that the precipitation variations are insufficient over the continental climate-dominated regions [9] and it is difficult for the limited precipitation to affect changes in glacier mass. However, a significant negative correlation (R < −0.6, P < 0.05; Figure 8c,g,k) is found between summer air temperature and mass balance. In contrast, annual air temperature is not significantly correlated with mass balance (P > 0.05; Figure 8d,h,l). This implies that annual air temperature is not a control factor of mass budget. Nonetheless, mass balance in the study area is primarily affected by the air temperature in summer because glacier mass loss or gain is influenced by the variation of glacier-wide albedo, the state of ice/snow, and the absorbed solar radiation in the glacier surface. This result is also consistent with that of the tree ring records in northeastern TP [66].

6. Discussions

6.1. Influence of the Local Factors on Glacier Status

As shown in Figure 9, the mass change magnitudes are remarkable different over the three glaciated regions in the same year, particularly in the extreme accumulation and ablation years. In general, the smallest value is detected in the XD glacier, the largest in the PIC, and the next largest in the GLDD. Considering their same locations in the interior TP, their glacier type and their lack of debris covering, the discrepancy of glacier status might stem from other local factors [9,67], including size, ELA, topography, or combination of these factors. Previous observations have shown the correlation between ELA or AAR changes and annual mass balance [17,19,20]. This relationship suggests that the glacier mass balance changes could be influenced by the change in glacier accumulation or ablation area. Compared with the PIC and GLDD, the XD glacier has the smallest glacier area and, the lowest ELA (Table 1), and the AAR dropped from 73.8% in the early 1990s to 51.0% in the period 2008–2012. Low AAR in recent years means higher albedo and mass balance variability for the XD glacier. Thus, the swift retreat seen in the XD glacier is probably a response to these factors, causing it to be more sensitive to climate change.
Conversely, the magnitude of glacier mass loss (increase) in the GLDD is slightly bigger (smaller) than the PIC, although the glacier–covered area in the GLDD is about two and a half times bigger. This may be attributed to the different topographic features over the two regions. At a nearly identical ELA level in the PIC and GLDD (Table 1), the PIC covers a glaciered area of more than 400 km2 and forms a rather flat plateau above about 5800 m [32]. Thus, the AAR in the PIC is about 70%, which is much bigger than 64% in the GLDD. Therefore, in similar conditions of air temperature and precipitations, glacier accumulation in the PIC is larger than in the GLDD. Besides, the GLDD consists of two major glaciated regions and more than 130 glaciers [60], thus the glacier distribution is more discrete and scattered (Figure 1) than in the PIC. Therefore, it may lead to greater acceleration of surface glacier melt than the PIC as well.

6.2. Potential and Limitations

In this study, we constructed the albedo-MB regression model by using the field mass balance measurements at the XD glacier from 2002 to 2010. The good agreement between the ELAs and albedo-based MB results at the XD glacier (see Figure 7a) demonstrates the capacity to predict specific mass balance in subsequent years after 2010. Noted that the mass balance records at XD glacier encompass very few values of large negative mass balance in 2006 and 2010, and these imbalance training samples probably lead to larger prediction errors in this regression model for certain years, especially when the glacier has larger mass loss. Therefore, good-distribution training samples, which better represent correlations between variations of both albedo and mass balance, are important for the regression model to predict robustly. In addition, the XD glacier has specific AAR and orientation, thereby possibly affecting the performance of the constructed model. More glaciers (with different areas, AARs and orientations etc.) used for model calibration can improve its accuracy and applicability.
Recently, some researchers have proposed that this albedo-based method may be extrapolated to other neighboring glaciers under similar climate conditions [21,22,23] based on the robust relationship between MODIS-derived albedo and annual mass balance. In this study, the good agreement between mass balance estimates derived from the albedo-based method and the geodetic method over the GLDD and PIC demonstrates that the albedo-MB regression model in the XD glacier can be utilized to reconstruct specific mass budgets for neighboring glaciers in the interior TP. Despite its great potential, some special attentions as follows should be paid when this method is used for further applications.
First, the studied glaciers should be the same types under similar climate conditions because the reactions of a glacier to climate change comprise a series of complex process [68]. Different atmospheric conditions, such as solar radiation, wind, air temperature, precipitation, cloudiness, evapotranspiration, etc., can influence energy and mass exchange in the glacier surface. Consequently, the physical mechanisms of glacier fluctuation will change in different climate environments. Moreover, the climate regime in which the glaciers are located must be far away from the influence of human activities, ensuring that their evolution mostly depends on regional climate variability. Second, to guarantee the robustness and accuracy of the constructed albedo-MB regression model, accurate and adequate in situ or geodetic mass balance measurements in the studied glaciers for calibration and verification are needed. For glaciers under different climatic conditions, the extrapolation and applicability of the albedo-based method require more comprehensive researches, and further model calibration by using air temperature and precipitation data should be investigated.
It should also be noted that the albedo-based method is not applicable to all glaciers. For glaciers with no accumulation zone in the ablation season, the glacier-wide albedo merely represents the average albedo of part of the glacier (most of the ablation zone). Thus, the derived mass balance will largely underestimate the real mass change. The method is also difficult to apply to glaciers with too small size (e.g., one pixel). This is because the contribution of off-glacier regions will contaminate the average glacier-wide albedo in the relatively coarse spatial resolution of the MODIS products. Moreover, this method is probably not suitable for debris-covered glaciers since the debris-covered area is usually classified as land rather than snow in the MODIS albedo products [34]. The applicability to surge glaciers needs an intensive study as well.

7. Conclusions

In this study, we constructed a liner regression model between the MODIS-derived annual minimum-averaged glacier-wide albedo (AMGA) and in situ observations of annual mass balance during 2002–2010 at the XD glacier, with a strong correlation (R2 = 0.941, P < 0.001). This albedo-MB regression model was employed to predict specific annual mass budgets over the period 2011–2016 for the XD glacier and to estimate, for the first time, the 17-year-long (2000–2016) annual mass balance series for the PIC and GLDD glaciers, which are close to the XD glacier and have similar climate regimes. An SLR analysis indicated that summer air temperature was one of the primary reasons for glacier shrinkage in the three studied areas.
The reconstructed 17-year-long annual mass balance series over the three studied glaciers confirmed that: (1) the derived albedo-MB regression model at the XD glacier could be extended to the neighboring GLDD glaciers and PIC with similar climate conditions, which was verified by mass balance estimates from glaciological, geodetic, and physical model-based methods; (2) the mass loss rate during 2000–2016 was 535 ± 63 mm w.e.a−1, 243 ± 66 mm w.e.a−1 and 113 ± 68 mm w.e.a−1 for the XD, GLDD, and PIC glaciers, respectively; and (3) the three studied regions exhibited a homogeneous tendency in glacier mass balance variations during the studied period, in which three significantly negative sequences occurred in 2006, 2010, and 2013.
This study demonstrates that the albedo-based method is potentially promising alternative to the geodetic method for deriving large-coverage and long-term annual mass balance over the interior TP where in situ measurements are scarce. This method merely depends on the in situ mass balance measurements and remote sensing-based glacier-wide albedo to establish a model and has no requirements for data continuity. Therefore, it can be applied to estimate mass balance for glaciers with inadequate or discontinued field measurements as well. The applicability of this albedo-based method to other regions of the TP and its surroundings (e.g., the Himalaya and Karakorum) needs intensive investigations. Moreover, although the continuous MODIS albedo products since 2000 are available, new sensors and platforms, such as the Visible Infrared Imager/Radiometer Suite (VIIRS) on the Suomi-NPP (National Polar-orbiting Partnership) satellite, are promising in providing global albedo products which are comparable with the MODIS [69,70]. This indicates that the albedo-based method could be further studied and applied for glacier mass balance estimation in the near future.

Supplementary Materials

The following are available online at https://www.mdpi.com/2072-4292/10/7/1031/s1, Table S1. Mean values of glacier-wide albedo retrieved from Landsat images at the Dongkemadi and XD glaciers. The albedo values in the table are the broadband albedo converted from the narrowband by using the method developed by Knap et al. [71]. The Landsat imageries were collected in the summer, from June to September. Figure S1. Standard deviation of the MODIS-derived glacier-wide albedo during the ablation season from 2000 to 2016: (a) XD glacier, (b) PIC and (c) GLDD. The mean value of the three regions is 0.09, 0.07, and 0.07, respectively. Table S2. The MODIS-derived mass balances (MBs) and its errors from 2000 to 2016 at the studied glacier regions.

Author Contributions

L.J. conceived and designed the experiments; Z.Z. performed the experiments and carried out the data analysis with the significant contributions of L.J. L.L. and H.W. made substantial contributions to the analysis and interpretation of the results; Y.S. focused on statistical computations; and Z.Z. and L.J. wrote the paper.

Funding

This research was funded by the Strategic Priority Research Program of the Chinese Academy of Sciences (grant No. XDA19070104), the National Key R & D Program of China (grant No. 2017YFA0603103), the National Natural Science Foundation of China (grant No. 41431070, 41590854, 41621091, and 41704023); and the Key Research Program of Frontier Sciences, CAS (grant No. QYZDB–SSW–DQC027 and QYZDJ–SSW–DQC042).

Acknowledgments

The MODIS daily albedo products were free downloaded at National Snow and Ice Data Center (NSIDC). Dr Marinka Spieß provided the ELA dataset in PIC. The authors would like to thank anonymous reviewers for their valuable comments and suggestions.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rangwala, I.; Miller, J.R.; Russell, G.L.; Xu, M. Using a global climate model to evaluate the influences of water vapor, snow cover and atmospheric aerosol on warming in the tibetan plateau during the twenty-first century. Clim. Dyn. 2009, 34, 859–872. [Google Scholar] [CrossRef]
  2. Immerzeel, W.W.; van Beek, L.P.H.; Bierkens, M.F.P. Climate change will affect the asian water towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
  3. Immerzeel, W.; Stoorvogel, J.; Antle, J. Can payments for ecosystem services secure the water tower of Tibet? Agric. Syst. 2008, 96, 52–63. [Google Scholar] [CrossRef]
  4. Azam, M.F.; Wagnon, P.; Berthier, E.; Vincent, C.; Fujita, K.; Kargel, J.S. Review of the status and mass changes of Himalayan-Karakoram glaciers. J. Glaciol. 2018, 64, 61–74. [Google Scholar] [CrossRef] [Green Version]
  5. Bolch, T.; Kulkarni, A.; Kääb, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M.; et al. The State and Fate of Himalayan Glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  6. Caidong, C.; Sorteberg, A. Modelled mass balance of Xibu glacier, Tibetan Plateau: Sensitivity to climate change. J. Glaciol. 2010, 56, 235–248. [Google Scholar] [CrossRef]
  7. Cao, B.; Pan, B.; Guan, W.; Wang, J.; Wen, Z. Changes in ice volume of the Ningchan No. 1 Glacier, China, from 1972 to 2014, as derived from in situ measurements. J. Glaciol. 2017, 63, 1025–1033. [Google Scholar] [CrossRef]
  8. Neckel, N.; Braun, A.; Kropácek, J.; Hochschild, V. Recent mass balance of the Purogangri Ice Cap, central Tibetan Plateau, by means of differential X-band SAR interferometry. Cryosphere 2013, 7, 1623–1633. [Google Scholar] [CrossRef] [Green Version]
  9. Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
  10. Yao, T.; Pu, J.; Lu, A.; Wang, Y.; Yu, W. Recent Glacial Retreat and Its Impact on Hydrol. Process. on the Tibetan Plateau, China, and Surrounding Regions. Arct. Antarct. Alp. Res. 2007, 39, 642–650. [Google Scholar] [CrossRef]
  11. Rabatel, A.; Sirguey, P.; Drolon, V.; Maisongrande, P.; Arnaud, Y.; Berthier, E.; Davaze, L.; Dedieu, J.; Dumont, M. Annual and Seasonal Glacier-Wide Surface Mass Balance Quantified from Changes in Glacier Surface State: A Review on Existing Methods Using Optical Satellite Imagery. Remote Sens. 2017, 9, 507. [Google Scholar] [CrossRef]
  12. Rabatel, A.; Dedieu, J.P.; Vincent, C. Spatio-temporal changes in glacier-wide mass balance quantified by optical remote sensing on 30 glaciers in the French Alps for the period 1983–2014. J. Glaciol. 2016, 62, 1153–1166. [Google Scholar] [CrossRef] [Green Version]
  13. Berthier, E.; Arnaud, Y.; Kumar, R.; Ahmad, S.; Wagnon, P.; Chevallier, P. Remote sensing estimates of glacier mass balances in the Himachal Pradesh (Western Himalaya, India). Remote Sens. Environ. 2007, 108, 327–338. [Google Scholar] [CrossRef] [Green Version]
  14. Kääb, A. Combination of SRTM3 and repeat ASTER data for deriving alpine glacier flow velocities in the Bhutan Himalaya. Remote Sens. Environ. 2005, 94, 463–474. [Google Scholar] [CrossRef]
  15. Nuimura, T.; Fujita, K.; Yamaguchi, S.; Sharma, R.R. Elevation changes of glaciers revealed by multitemporal digital elevation models calibrated by GPS survey in the Khumbu region, Nepal Himalaya, 1992–2008. J. Glaciol. 2012, 58, 648–656. [Google Scholar] [CrossRef]
  16. Li, J.; Li, Z.; Zhu, J.; Li, X.; Xu, B.; Wang, Q.; Huang, C.; Hu, J. Early 21st century glacier thickness changes in the Central Tien Shan. Remote Sens. Environ. 2017, 192, 12–29. [Google Scholar] [CrossRef]
  17. Braithwaite, R.J. Can the Mass Balance of a Glacier be Estimated from its Equilibrium-Line Altitude? J. Glaciol. 1984, 30, 364–368. [Google Scholar] [CrossRef] [Green Version]
  18. Rabatel, A.; Dedieu, J.P.; Vincent, C. Using remote-sensing data to determine equilibrium-line altitude and mass-balance time series: Validation on three french glaciers, 1994–2002. J. Glaciol. 2005, 51, 539–546. [Google Scholar] [CrossRef]
  19. Dyurgerov, M.; Meier, M.F.; Bahr, D.B. A new index of glacier area change: A tool for glacier monitoring. J. Glaciol. 2009, 55, 710–716. [Google Scholar] [CrossRef]
  20. Dyurgerov, M.B.; Meier, M.F. Glaciers and the Changing Earth System: A 2004 Snapshot; Institute of Arctic and Alpine Research, University of Colorado: Boulder, CO, USA, 2005; Volume 58, p. 23. [Google Scholar]
  21. Brun, F.; Dumont, M.; Wagnon, P.; Berthier, E.; Azam, M.F.; Shea, J.M.; Sirguey, P.; Rabatel, A.; Ramanathan, A. Seasonal changes in surface albedo of himalayan glaciers from MODIS data and links with the annual mass balance. Cryosphere 2015, 9, 341–355. [Google Scholar] [CrossRef]
  22. Dumont, M.; Gardelle, J.; Sirguey, P.; Guillot, A.; Six, D.; Rabatel, A.; Arnaud, Y. Linking glacier annual mass balance and glacier albedo retrieved from MODIS data. Cryosphere 2012, 6, 1527–1539. [Google Scholar] [CrossRef] [Green Version]
  23. Sirguey, P.; Still, H.; Cullen, N.J.; Dumont, M.; Arnaud, Y.; Conway, J.P. Reconstructing the mass balance of brewster glacier, new zealand, using modis-derived glacier-wide albedo. Cryosphere 2016, 10, 2465–2484. [Google Scholar] [CrossRef]
  24. Davaze, L.; Rabatel, A.; Arnaud, Y.; Sirguey, P.; Six, D.; Letreguilly, A.; Dumont, M. Monitoring glacier albedo as a proxy to derive summer and annual surface mass balances from optical remote-sensing data. Cryosphere 2018, 12, 271–286. [Google Scholar] [CrossRef] [Green Version]
  25. Liu, S.; Zhang, Y.; Zhang, Y.; Ding, Y. Estimation of glacier runoff and future trends in the Yangtze River source region, China. J. Glaciol. 2009, 55, 353–362. [Google Scholar] [CrossRef] [Green Version]
  26. Zhang, Y.; Liu, S.; Xu, J.; Shangguan, D. Glacier change and glacier runoff variation in the Tuotuo River basin, the source region of Yangtze River in western China. Environ. Geol. 2008, 56, 59–68. [Google Scholar] [CrossRef]
  27. Liang, E.; Shao, X.; Qin, N. Tree–ring based summer temperature reconstruction for the source region of the Yangtze River on the Tibetan Plateau. Glob. Planet. Chang. 2008, 61, 313–320. [Google Scholar] [CrossRef]
  28. Shi, Y.; Li, J. Glaciological research of the Qinghai-Xizang Plateau in China. J. Geogr. 1981, 90, 203–209. (In Japanese) [Google Scholar] [CrossRef]
  29. Wang, J.; Cui, Y.; He, X.; Zhang, J.; Yan, S. Surface Albedo Variation and Its Influencing Factors over Dongkemadi Glacier, Central Tibetan Plateau. Adv. Meteorol. 2015. [Google Scholar] [CrossRef]
  30. Fujita, K.; Ageta, Y.; Pu, J.; Yao, T. Mass balance of Xiao Dongkemadi glacier on the central Tibetan Plateau from 1989 to 1995. Ann. Glaciol. 2000, 31, 159–163. [Google Scholar] [CrossRef]
  31. Yi, C.; Li, X.; Qu, J. Quaternary glaciation of Puruogangri—The largest modern ice field in Tibet. Quat. Int. 2002, 97–98, 111–121. [Google Scholar] [CrossRef]
  32. Liu, L.; Jiang, L.; Sun, Y.; Wang, H.; Yi, C.; Hsu, H. Morphometric Controls on Glacier Mass Balance of the Puruogangri Ice Field, Central Tibetan Plateau. Water 2016, 8, 496. [Google Scholar] [CrossRef]
  33. Huintjes, E.; Neckel, N.; Hochschild, V.; Schneider, C. Surface energy and mass balance at Purogangri ice cap, central Tibetan Plateau, 2001–2011. J. Glaciol. 2015, 61, 1048–1060. [Google Scholar] [CrossRef] [Green Version]
  34. Spiess, M.; Maussion, F.; Möller, M.; Scherer, D.; Schneider, C. MODIS Derived Equilibrium Line Altitude Estimates for Purogangri Ice Cap, Tibetan Plateau, and their Relation to Climatic Predictors (2001–2012). Geogr. Ann. Ser. A Phys. Geogr. 2015, 97, 599–614. [Google Scholar] [CrossRef]
  35. Zhou, W.; Li, Z.; Li, J.; Cui, Z.; Wang, C. Variations of glaciers and glacial lake in geladandong mountain range in 1992–2009 with remote-sensing technology. J. Cent. South Univ. T. 2014, 45, 3505–3512. (In Chinese) [Google Scholar]
  36. Wang, J.; He, X.; Ye, B.; Yang, G. Variations of Albedo on the DongkemadiGlacier, Tanggula Range. J. Glaciol. Geocryol. 2012, 34, 21–28. (In Chinese) [Google Scholar]
  37. Zhang, J.; He, X.; Ye, B.; Wu, J. Recent variation of mass balance of the xiao dongkemadi glacier in the tanggula range and its influencing factors. J. Glaciol. Geocryol. 2013, 35, 263–271. (In Chinese) [Google Scholar]
  38. Pu, J.; Yao, T.; Wang, N.; Ding, L.; Zhang, Q. Puruogangri Ice Field and Its Variations Since the Little Ice Age of the Northern Tibetan Plateau. J. Glaciol. Geocryol. 2002, 24, 87–92. (In Chinese) [Google Scholar]
  39. Lei, Y.; Yao, T.; Yi, C.; Wang, W.; Sheng, Y.; Li, J.; Joswiak, D. Glacier mass loss induced the rapid growth of Linggo Co on the central Tibetan Plateau. J. Glaciol. 2012, 58, 177–184. [Google Scholar] [CrossRef]
  40. Liu, L.; Jiang, L.; Sun, Y.; Yi, C.; Wang, H.; Hsu, H. Glacier elevation changes (2012–2016) of the Puruogangri Ice Field on the Tibetan Plateau derived from bi-temporal TanDEM-X InSAR data. Int. J. Remote Sens. 2016, 37, 5687–5707. [Google Scholar] [CrossRef]
  41. Ye, Q.; Kang, S.; Chen, F.; Wang, J. Monitoring glacier variations on Geladandong mountain, central Tibetan Plateau, from 1969 to 2002 using remote-sensing and GIS technologies. J. Glaciol. 2006, 52, 537–545. [Google Scholar] [CrossRef]
  42. Zhang, J.; Liu, Y.; Lv, T.; Wang, Y.; Tao, F. An inventory of glacier change for the Geladandong Mountain area, China. J. Arid Land Resour. Environ. 2015, 29, 184–189. (In Chinese) [Google Scholar]
  43. Pu, J.; Yao, T.; Yang, M.; Tian, L.; Wang, N.; Ageta, Y.; Fujita, K. Rapid decrease of mass balance observed in the Xiao (Lesser) Dongkemadi Glacier, in the central Tibetan Plateau. Hydrol. Process. 2008, 22, 2953–2958. [Google Scholar] [CrossRef]
  44. Liu, L. Glacier Mass Balances in the Tibetan Plateau Observed from SAR Interferometry; University of Chinese Academy of Sciences: Beijing, China, 2016. [Google Scholar]
  45. Sun, Y.; Jiang, L.; Liu, L.; Sun, Q.; Wang, H.; Hsu, H. Mapping Glacier Elevations and Their Changes in the Western Qilian Mountains, Northern Tibetan Plateau, by Bistatic InSAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 68–78. [Google Scholar] [CrossRef]
  46. Williamson, S.N.; Copland, L.; Hik, D.S. The accuracy of satellite-derived albedo for northern alpine and glaciated land covers. Polar Sci. 2016, 10, 262–269. [Google Scholar] [CrossRef]
  47. Klein, A.G.; Stroeve, J. Development and validation of a snow albedo algorithm for the MODIS instrument. Ann. Glaciol. 2002, 34, 45–52. [Google Scholar] [CrossRef]
  48. Hall, D.K.; Riggs, G.A. Accuracy assessment of the MODIS snow products. Hydrol. Process. 2007, 21, 1534–1547. [Google Scholar] [CrossRef]
  49. Maussion, F.; Scherer, D.; Mölg, T.; Collier, E.; Curio, J.; Finkelnburg, R. Precipitation seasonality and variability over the Tibetan Plateau as resolved by the High Asia Reanalysis. J. Clim. 2014, 27, 1910–1927. [Google Scholar] [CrossRef]
  50. Curio, J.; Maussion, F.; Scherer, D. A 12-year high-resolution climatology of atmospheric water transport over the Tibetan Plateau. Earth Syst. Dyn. 2015, 6, 109–124. [Google Scholar] [CrossRef] [Green Version]
  51. Mölg, T.; Maussion, F.; Scherer, D. Mid-latitude westerlies as a driver of glacier variability in monsoonal High Asia. Nat. Clim. Chang. 2014, 4, 68–73. [Google Scholar] [CrossRef]
  52. York, D.; Evensen, N.M.; Martínez, M.L.; De Basabe Delgado, J. Unified equations for the slope, intercept, and standard errors of the best straight line. Am. J. Phys. 2004, 72, 367–375. [Google Scholar] [CrossRef]
  53. Senese, A.; Maugeri, M.; Meraldi, E.; Verza, G.P.; Azzoni, R.S.; Compostella, C.; Diolaiuti, G. Estimating the snow water equivalent on a glacierized high elevation site (forni glacier, italy). Cryosphere 2018, 12, 1293–1306. [Google Scholar] [CrossRef]
  54. Stroeve, J.C.; Box, J.E.; Haran, T. Evaluation of the MODIS (MOD10A1) daily snow albedo product over the Greenland ice sheet. Remote Sens. Environ. 2006, 105, 155–171. [Google Scholar] [CrossRef]
  55. Tekeli, A.E.; Şensoy, A.; Şorman, A.; Akyürek, Z.; Şorman, Ü. Accuracy assessment of MODIS daily snow albedo retrievals with in situ measurements in Karasu basin, Turkey. Hydrol. Process. 2006, 20, 705–721. [Google Scholar] [CrossRef]
  56. Wu, X.; Wang, N.; Lu, A.; Pu, J.; Guo, Z.; Zhang, H. Variations in Albedo on Dongkemadi Glacier in Tanggula Range on the Tibetan Plateau during 2002–2012 and Its Linkage with Mass Balance. Arct. Antarct. Alp. Res. 2015, 47, 281–292. [Google Scholar] [CrossRef] [Green Version]
  57. Wang, H.; Jia, L.; Steffen, H.; Wu, P.; Jiang, L.; Hsu, H.; Xiang, L.; Wang, Z.; Hu, B. Increased water storage in north america and scandinavia from grace gravity data. Nat. Geosci. 2012, 6, 38–42. [Google Scholar] [CrossRef]
  58. Ke, L.; Ding, X.; Li, W.; Qiu, B. Remote Sensing of Glacier Change in the Central Qinghai-Tibet Plateau and the Relationship with Changing Climate. Remote Sens. 2017, 9, 114. [Google Scholar] [CrossRef]
  59. Chao, N.; Wang, Z.; Hwang, C.; Jin, T.; Cheng, Y.S. Decline of Geladandong Glacier Elevation in Yangtze River’s Source Region: Detection by ICESat and Assessment by Hydroclimatic Data. Remote Sens. 2017, 9, 75. [Google Scholar] [CrossRef]
  60. Liu, G.; Fan, J.; Zhao, F.; Mao, K.; Dou, C. Monitoring elevation change of glaciers on Geladandong Mountain using TanDEM-X SAR interferometry. J. Mt. Sci. 2017, 14, 859–869. [Google Scholar] [CrossRef]
  61. Chen, A.; Wang, N.; Li, Z.; Wu, Y.; Zhang, W.; Guo, Z. Region–wide glacier mass budgets for the Tanggula Mountains between ~1969 and ~2015 derived from remote sensing data. Arct. Antarct. Alp. Res. 2017, 49, 551–568. [Google Scholar] [CrossRef]
  62. Bhambri, R.; Hewitt, K.; Kawishwar, P.; Pratap, B. Surge-type and surge-modified glaciers in the Karakoram. Sci. Rep. 2017, 7, 15391. [Google Scholar] [CrossRef] [PubMed]
  63. Zhang, Y.; Fujita, K.; Ageta, Y.; Nakawo, M.; Yao, T.; Pu, J. The response of glacier ELA to climate fluctuations on High-Asia. Bull. Glacier Res. 1998, 16, 1–11. [Google Scholar] [CrossRef]
  64. Dyurgerov, M.B.; Meier, M.F. Twentieth century climate change: Evidence from small glaciers. Proc. Natl. Acad. Sci. USA 1999, 97, 1406–1411. [Google Scholar] [CrossRef]
  65. Pepin, N.; Bradley, R.S.; Diza, H.F.; Baraer, M.; Caceres, E.B.; Forsythe, N.; Fowler, H.; Greenwood, G.; Hashmi, M.Z.; et al. Elevation–dependent warming in mountain regions of the world. Nat. Clim. Chang. 2015, 5, 424–430. [Google Scholar] [CrossRef] [Green Version]
  66. Gou, X.; Chen, F.; Yang, M.; Jacoby, G.; Peng, J.; Zhang, Y. A comparison of tree-ring records and glacier variations over the past 700 years, northeastern Tibetan Plateau. Ann. Glaciol. 2006, 43, 86–90. [Google Scholar] [CrossRef]
  67. Oerlemans, J.; Anderson, B.; Hubbard, A.; Huybrechts, P.; Johannesson, T.; Knap, W.H.; Schmeits, M.; Stroeven, A.P.; van de Wal, R.S.W.; Wallinga, J.; et al. Modelling the response of glaciers to climate warming. Clim. Dyn. 1998, 14, 267–274. [Google Scholar] [CrossRef] [Green Version]
  68. Nye, J.F. The response of glaciers and ice–sheets to seasonal and climatic changes. Proc. R. Soc. Lond. A. 1960, 256, 559–584. [Google Scholar] [CrossRef]
  69. Schaaf, C.B.; Liu, J.; Gao, F.; Strahler, A.H. Aqua and Terra MODIS albedo and reflectance anisotropy products. In Land Remote Sensing and Global Environmental Change; Springer: New York, NY, USA, 2010; pp. 549–561. [Google Scholar]
  70. Liu, Y.; Wang, Z.; Sun, Q.; Erb, A.M.; Li, Z.; Schaaf, C.B.; Zhang, X.; Román, M.O.; Scott, R.L.; Zhang, Q.; et al. Evaluation of the viirs brdf, albedo and nbar products suite and an assessment of continuity with the long term modis record. Remote Sens. Environ. 2017, 201, 256–274. [Google Scholar] [CrossRef]
  71. Knap, W.H.; Reijmer, C.H.; Oerlemans, J. Narrowband to broadband conversion of Landsat TM glacier albedos. Int. J. Remote Sens. 1999, 20, 2091–2110. [Google Scholar] [CrossRef]
Remotesensing 10 01031 g001 550
Figure 1. (a) Geographical location of the studied glaciated regions in the interior Tibetan Plateau (TP). The glacier-covered areas in (b) the Dongkemadi glacier, (c) the Geladandong mountain region (GLDD), and (d) the Purogangri ice cap (PIC). The Xiao Dongkemadi (XD) glacier is a tributary of the Dongkemadi glacier, which is indicated by the arrow in panel (b). The GLDD consists of two parts: the western and eastern parts, which are indicated by the arrows in panel (c). The red circle points in (b–d) represent grid cells (10 km resolution) of the High Asia Refined analysis (HAR) data products. The HAR grids are used for air temperature and precipitation estimation in this study. Base maps of the three glaciated regions were downloaded from Google Earth.
Figure 1. (a) Geographical location of the studied glaciated regions in the interior Tibetan Plateau (TP). The glacier-covered areas in (b) the Dongkemadi glacier, (c) the Geladandong mountain region (GLDD), and (d) the Purogangri ice cap (PIC). The Xiao Dongkemadi (XD) glacier is a tributary of the Dongkemadi glacier, which is indicated by the arrow in panel (b). The GLDD consists of two parts: the western and eastern parts, which are indicated by the arrows in panel (c). The red circle points in (b–d) represent grid cells (10 km resolution) of the High Asia Refined analysis (HAR) data products. The HAR grids are used for air temperature and precipitation estimation in this study. Base maps of the three glaciated regions were downloaded from Google Earth.
Remotesensing 10 01031 g001
Remotesensing 10 01031 g002 550
Figure 2. Flowchart of data processing and result analysis.
Figure 2. Flowchart of data processing and result analysis.
Remotesensing 10 01031 g002
Remotesensing 10 01031 g003 550
Figure 3. An albedo-mass balance (MB) regression model between annual mass balance and annual minimum-averaged glacier-wide albedo (AMGA) at the XD glacier from 2002 to 2010. The red dashed line is the 95% prediction interval.
Figure 3. An albedo-mass balance (MB) regression model between annual mass balance and annual minimum-averaged glacier-wide albedo (AMGA) at the XD glacier from 2002 to 2010. The red dashed line is the 95% prediction interval.
Remotesensing 10 01031 g003
Remotesensing 10 01031 g004 550
Figure 4. Temporal variations of the MODIS-derived glacier-wide albedo during the ablation season from 2000 to 2016: (a) XD glacier, (b) PIC, and (c) GLDD.
Figure 4. Temporal variations of the MODIS-derived glacier-wide albedo during the ablation season from 2000 to 2016: (a) XD glacier, (b) PIC, and (c) GLDD.
Remotesensing 10 01031 g004
Remotesensing 10 01031 g005 550
Figure 5. Annual minimum-averaged glacier-wide albedo (AMGA) from 2000 to 2016 at: (a) XD glacier, (b) PIC and (c) GLDD. Please note that the error bars in the PIC and GLDD are multiplied by eight times.
Figure 5. Annual minimum-averaged glacier-wide albedo (AMGA) from 2000 to 2016 at: (a) XD glacier, (b) PIC and (c) GLDD. Please note that the error bars in the PIC and GLDD are multiplied by eight times.
Remotesensing 10 01031 g005
Remotesensing 10 01031 g006 550
Figure 6. MODIS-derived annual mass balances series from 2000 to 2016 at: (a) XD glacier, (b) PIC, and (c) GLDD. Blue dotted lines in (a) represent the field observations during the period 2000–2010. The red line (or shadow) represents the annual mean (or error) result of the geodetic method. The uncertainty of estimated mass balance (black error line) is shown in every panel. Note the scaling of mass balance is different on three panels.
Figure 6. MODIS-derived annual mass balances series from 2000 to 2016 at: (a) XD glacier, (b) PIC, and (c) GLDD. Blue dotted lines in (a) represent the field observations during the period 2000–2010. The red line (or shadow) represents the annual mean (or error) result of the geodetic method. The uncertainty of estimated mass balance (black error line) is shown in every panel. Note the scaling of mass balance is different on three panels.
Remotesensing 10 01031 g006
Remotesensing 10 01031 g007 550
Figure 7. Comparisons of MODIS-derived mass balance series and ELAs at: (a) XD glacier and (b) PIC. The ELAs at XD glacier were obtained from Landsat imagery, while ELAs at the PIC were calculated by Spieß et al. [34] from the MODIS data. Please note that the years of ELA estimate in 2012 at XD glacier and 2007 at the PIC are absent because of the lack of valid data.
Figure 7. Comparisons of MODIS-derived mass balance series and ELAs at: (a) XD glacier and (b) PIC. The ELAs at XD glacier were obtained from Landsat imagery, while ELAs at the PIC were calculated by Spieß et al. [34] from the MODIS data. Please note that the years of ELA estimate in 2012 at XD glacier and 2007 at the PIC are absent because of the lack of valid data.
Remotesensing 10 01031 g007
Remotesensing 10 01031 g008 550
Figure 8. Correlations between mass balance and total (summer and annual precipitation) or means (summer and annual air temperature) local climate indicators from simple linear regression (SLR) analysis in (a–d) the XD glacier, (e–h) the PIC and (i–l) the GLDD. Dashed gray lines represent the changing trend with the indicators. The summer season corresponds to the months June to September.
Figure 8. Correlations between mass balance and total (summer and annual precipitation) or means (summer and annual air temperature) local climate indicators from simple linear regression (SLR) analysis in (a–d) the XD glacier, (e–h) the PIC and (i–l) the GLDD. Dashed gray lines represent the changing trend with the indicators. The summer season corresponds to the months June to September.
Remotesensing 10 01031 g008
Remotesensing 10 01031 g009 550
Figure 9. Reconstructed mass balances from 2000 to 2016 at three glaciated regions in the interior TP.
Figure 9. Reconstructed mass balances from 2000 to 2016 at three glaciated regions in the interior TP.
Remotesensing 10 01031 g009
Table
Table 1. Topographical and climatic characteristics of the studied glaciated regions in the interior TP. Please note that annual air temperature and precipitation are generated from High Asia Refined analysis (HAR) data.
Table 1. Topographical and climatic characteristics of the studied glaciated regions in the interior TP. Please note that annual air temperature and precipitation are generated from High Asia Refined analysis (HAR) data.
VariableXDPICGLDD
Location33°04′ N,92°05′ E33°53′ N, 89°10′ E33°30′ N, 91°10′ E
Surface area (km2)1.77420845
Number of glaciers159142
ELA (m a.s.l.)562057505740
Max. elevation (m a.s.l.)592663706621
Min. elevation (m a.s.l.)538053505200
Annual air temperature (°C)−8.10 ± 0.63−9.76 ± 0.86−9.25 ± 0.78
Annual precipitation (mm)302 ± 47248 ± 30301 ± 56
TypeContinental glacierContinental glacierContinental glacier
Table
Table 2. Datasets used in this study.
Table 2. Datasets used in this study.
Data typeSourcesDateUtilization
Annual mass balance seriesIn situ observations at XD2000–2010Model reconstruction and validation
Average annual mass balanceGeodetic estimates [40,44]2000–2016Result verification
Daily AlbedoMOD10A1/MYD10A12000–2016Glacier-wide albedo calculation
Monthly precipitationand air temperatureHAR2001–2013Influence on glacier change
Table
Table 3. The leave-one-out cross-validation (LOOCV) for the albedo-MB regression model. The regression parameters of A and B refer to the slope and intercept in the liner regression model.
Table 3. The leave-one-out cross-validation (LOOCV) for the albedo-MB regression model. The regression parameters of A and B refer to the slope and intercept in the liner regression model.
YearMass Balance in the j Year/mm w.e.LOOCV Mass Balance/mm w.e.Regression Parameters (A and B)
2002−583−5184346.9 and −2314.9
20034−724277.1 and −2299.8
2004−153−2134331.1 and −2321.8
2005−177−2794322.8 and −2322.8
2006−917−10444653.4 and −2471.4
2007−591−5344347.2 and −2315.9
2008−801754848.6 and −2514.9
2009−91−2054283.2 and −2306.8
2010−1066−9154058.7 and −2178.4
Mean−406−400.604385.44 and −2338.52
Standard Deviation––230.51 and 99.06
Table
Table 4. Comparison of glacier mass balance estimation for three regions from previously published studies and this study.
Table 4. Comparison of glacier mass balance estimation for three regions from previously published studies and this study.
GlaciersMass Balance/mm w.e.a−1PeriodArea/km2StudyMethod 1Relative Error 2/%
XD−740 ± 2101999–201573.60 3Chen et al., 2017 [59]Geod.
−3582000–2010–Yao et al., 2012 [9]Glac.
−339 ± 372000–2012 473.60 3Liu, 2016 [44]Geod.
−379 ± 772000–20111.77Our studyAlbe.11.80
PIC−44 2001–2011420Huintjes et al., 2015 [33]Phys.
−44 ± 152000–2012 5408Neckel et al., 2013 [8]Geod.
−46 ± 822000–2011420Our studyAlbe.4.55
−269 ± 252012–2016 6420Liu et al., 2016 [40]Geod.
−294 ± 1342012–2015420Our studyAlbe.9.23
GLDD−330 ± 3801999–2015178 (West)Chen et al., 2017 [59]Geod.
−134 ± 562003–2009845Chao et al., 2017 [60]Geod.
−140 ± 2602000–2014277(West)Liu et al., 2017 [61]Geod.
−128 ± 492000–2012 7845Liu, 2016 [44]Geod.
−143 ± 802000–2011845Our studyAlbe.11.72
−89 ± 482000–2012 7185 (West)Liu, 2016 [44]Geod.
−202 ± 792000–2011185 (West)Our studyAlbe.
−155 ± 482000–2012660 (East)Liu, 2016 [44]Geod.
−146 ± 802000–2011660 (East)Our studyAlbe.
Note: 1 Geod., geodetic method; Glac., glaciological method; Albe., albedo-based method; Phys., physical model-based method. 2 Relative error is absolute error (between our method and the geodetic method irrespective of their uncertainties) divided by the magnitude of the corresponding geodetic value in the same study period. 3 The Dongkemadi Region. 4 From February 2000 to February 2012. 5 From February 2000 to January 2012. 6 From January 2012 to January 2016. 7 From February 2000 to March 2012.

Share and Cite

MDPI and ACS Style

Zhang, Z.; Jiang, L.; Liu, L.; Sun, Y.; Wang, H. Annual Glacier-Wide Mass Balance (2000–2016) of the Interior Tibetan Plateau Reconstructed from MODIS Albedo Products. Remote Sens. 2018, 10, 1031. https://doi.org/10.3390/rs10071031

AMA Style

Zhang Z, Jiang L, Liu L, Sun Y, Wang H. Annual Glacier-Wide Mass Balance (2000–2016) of the Interior Tibetan Plateau Reconstructed from MODIS Albedo Products. Remote Sensing. 2018; 10(7):1031. https://doi.org/10.3390/rs10071031

Chicago/Turabian Style

Zhang, Zhimin, Liming Jiang, Lin Liu, Yafei Sun, and Hansheng Wang. 2018. "Annual Glacier-Wide Mass Balance (2000–2016) of the Interior Tibetan Plateau Reconstructed from MODIS Albedo Products" Remote Sensing 10, no. 7: 1031. https://doi.org/10.3390/rs10071031

APA Style

Zhang, Z., Jiang, L., Liu, L., Sun, Y., & Wang, H. (2018). Annual Glacier-Wide Mass Balance (2000–2016) of the Interior Tibetan Plateau Reconstructed from MODIS Albedo Products. Remote Sensing, 10(7), 1031. https://doi.org/10.3390/rs10071031

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop