Radiation Component Calculation and Energy Budget Analysis for the Korean Peninsula Region
Abstract
:1. Introduction
2. Data
3. Calculation of Radiation Components and Energy Budget
3.1. Shortwave Radiation Compoents
3.1.1. ISR
3.1.2. RSR
3.1.3. DSR and ASR
3.2. Longwave Radiation Components
3.2.1. OLR
3.2.2. DLR
3.2.3. ULR
3.3. Calibration Using CERES and MERRA-2 Data
3.4. Energy Budget
4. Results
4.1. Verification of Calculated Radiation Components
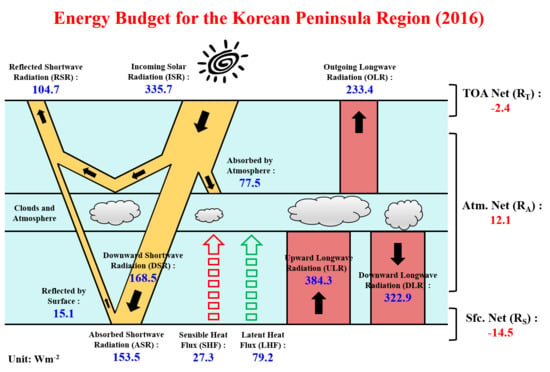
4.2. Energy Budget of the Korean Peninsula Region
4.3. Regional Energy Budgets within the Korean Peninsula
5. Summary and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| AHI | Advanced Himawari Imager |
| ASR | Absorbed Shortwave Radiation |
| CERES | Cloud and Earth’s Radiant Energy System |
| DLR | Downward Longwave Radiation |
| DSR | Downward Shortwave Radiation |
| ISR | Incoming Solar Radiation |
| LDAPS | Local Data Assimilation and Prediction System |
| LHF | Latent Heat Flux |
| MERRA-2 | Modern Era Retrospective Analysis for Research and Applications Version 2 |
| OLR | Outgoing Longwave Radiation |
| RSR | Reflected Shortwave Radiation |
| SHF | Sensible Heat Flux |
| ULR | Upward Longwave Radiation |
References
- Houghton, J.T.; Ding, Y.; Griggs, D.J.; Noguer, N.; van der Linden, P.J.; Xiaosu, D.; Maskell, K.; Johnson, C.A. Climate Change 2001: The Scientific Basis; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Solomon, S. Climate Change 2007: The Physical Science Basis: Working Group I Contribution to the Fourth Assessment Report of the IPCC (Vol. 4); Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Stocker, T. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Lashof, D.A.; Ahuja, D.R. Relative contributions of greenhouse gas emissions to global warming. Nature 1990, 344, 529–531. [Google Scholar] [CrossRef]
- Vitousek, P.M.; Mooney, H.A.; Lubchenco, J.; Melillo, J.M. Human domination of Earth’s ecosystems. Science 1997, 277, 494–499. [Google Scholar] [CrossRef]
- Karl, T.R.; Trenberth, K.E. Modern global climate change. Science 2003, 302, 1719–1723. [Google Scholar] [CrossRef] [PubMed]
- Smith, G.L.; Gibson, G.G.; Harrison, E.F. History of Earth Radiation Budget at Langley Research Center. Available online: https://ams.confex.com/ams/pdfpapers/158948.pdf (accessed on 1 February 2018).
- Walther, G.R.; Post, E.; Convey, P.; Menzel, A.; Parmesan, C.; Beebee, T.J.C.; Fromentin, J.M.; Hoegh-Guldberg, O.; Bairlein, F. Ecological responses to recent climate change. Nature 2002, 416, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Root, T.L.; Price, J.T.; Hall, K.R.; Schneider, S.H. Fingerprints of global warming on wild animals and plants. Nature 2003, 421, 57–60. [Google Scholar] [CrossRef] [PubMed]
- McMichael, A.J.; Woodruff, R.E.; Hales, S. Climate change and human health: Present and future risks. Lancet 2006, 367, 859–869. [Google Scholar] [CrossRef]
- O’Brien, G.; O’Keefe, P.; Rose, J.; Wisner, B. Climate change and disaster management. Disasters 2006, 30, 64–80. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bouwer, L.M. Have disaster losses increased due to anthropogenic climate change? Bull. Am. Meteorol. Soc. 2011, 92, 39–46. [Google Scholar] [CrossRef]
- Nordhaus, W.D. Managing the Global Commons: The Economics of Climate Change (Vol. 31); MIT Press: Cambridge, UK, 1994. [Google Scholar]
- Pielke, R.A.; Marland, G.; Betts, R.A.; Chase, T.N.; Eastman, J.L.; Niles, J.O.; Running, S.W. The influence of land-use change and landscape dynamics on the climate system: Relevance to climate-change policy beyond the radiative effect of greenhouse gases. Philos. Trans. R. Soc. Lond. A 2002, 360, 1705–1719. [Google Scholar] [CrossRef] [PubMed]
- Gaffin, S.; Rosenzweig, C.; Parshall, L.; Beattie, D.; Berghage, R.; O’Keeffe, G.; Braman, D. Energy Balance Modeling Applied to a Comparison of White and Green Roof Cooling Efficiency. In Green Roofs in the New York Metropolitan Region Research Report; Columbia University Center for Climate Systems Research and NASA Goddard Institute for Space Studies: New York, NY, USA, 2010. [Google Scholar]
- Sheffield, P.E.; Landrigan, P.J. Global climate change and children’s health: Threats and strategies for prevention. Environ. Health Perspect. 2011, 119, 291–298. [Google Scholar] [CrossRef] [PubMed]
- Coutts, A.M.; Harris, R. A multi-scale assessment of urban heating in Melbourne during an extreme heat event and policy approaches for adaptation. In Melbourne: Victorian Centre for Climate Change and Adaptation Research; Monash University: Clayton, Australia, 2013. [Google Scholar]
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s global energy budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–323. [Google Scholar] [CrossRef]
- Wild, M.; Folini, D.; Hakuba, M.Z.; Schär, C.; Seneviratne, S.I.; Kato, S.; Rutan, D.; Ammann, C.; Wood, E.F.; König-Langlo, G. The energy balance over land and oceans: An assessment based on direct observations and CMIP5 climate models. Clim. Dyn. 2015, 44, 3393–3429. [Google Scholar] [CrossRef]
- Barkstrom, B.R. The Earth Radiation Budget Experiment (ERBE). Bull. Am. Meteorol. Soc. 1984, 65, 1170–1185. [Google Scholar] [CrossRef] [Green Version]
- Wielicki, B.A.; Barkstrom, B.R.; Harrison, E.F.; Lee, R.B.; Smith, G.L.; Cooper, J.E. Clouds and the Earth’s Radiant Energy System (CERES): An earth observing system experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Barkstrom, B.R.; Baum, B.A.; Charlock, T.P.; Green, R.N.; Kratz, D.P.; Lee, R.B.; Minnis, P.; Smith, G.L.; Wong, T.; et al. Clouds and the Earth’s Radiant Energy System (CERES): Algorithm overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1127–1141. [Google Scholar] [CrossRef]
- Loeb, N.G.; Priestley, K.J.; Kratz, D.P.; Geier, E.B.; Green, R.N.; Wielicki, B.A.; Hinton, P.O.; Nolan, S.K. Determination of unfiltered radiances from the clouds and the earth’s radiant energy system instrument. J. Appl. Meteorol. 2001, 40, 822–835. [Google Scholar] [CrossRef]
- Kato, S.; Loeb, N.G.; Rose, F.G.; Doelling, D.R.; Rutan, D.A.; Caldwell, T.E.; Yu, L.; Weller, R.A. Surface irradiances consistent with CERES-derived top-of-atmosphere shortwave and longwave irradiances. J. Clim. 2013, 26, 2719–2740. [Google Scholar] [CrossRef]
- L’Ecuyer, T.S.; Beaudoing, H.K.; Rodell, M.; Olson, W.; Lin, B.; Kato, S.; Clayson, C.A.; Wood, E.; Sheffield, J.; Adler, R.; et al. The observed state of the energy budget in the early twenty-first century. J. Clim. 2015, 28, 8319–8346. [Google Scholar] [CrossRef]
- Matthews, G. In-flight spectral characterization and calibration stability estimates for the clouds and the earth’s radiant energy system (CERES). J. Atmos. Ocean. Technol. 2009, 26, 1685–1716. [Google Scholar] [CrossRef]
- Ma, Q.; Wang, K.; Wild, M. Impact of geolocations of validation data on the evaluation of surface incident shortwave radiation from Earth System Models. J. Geophys. Res. Atmos. 2015, 120, 6825–6844. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Liang, S.; Wild, M.; Jiang, B. Analysis of surface incident shortwave radiation from four satellite products. Remote Sens. Environ. 2015, 165, 186–202. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, S.; Wang, G.; Yao, Y.; Jiang, B.; Cheng, J. Evaluation of the reanalysis surface incident shortwave radiation products from NCEP, ECMWF, GSFC, and JMA using satellite and surface observations. Remote Sens. 2016, 8, 225. [Google Scholar] [CrossRef]
- Ramanathan, V. The role of earth radiation budget studies in climate and general circulation research. J. Geophys. Res. Atmos. 1987, 92, 4075–4095. [Google Scholar] [CrossRef]
- Kiehl, J.T.; Trenberth, K.E. Earth’s annual global mean energy budget. Bull. Am. Meteorol. Soc. 1997, 78, 197–208. [Google Scholar] [CrossRef]
- Loeb, N.G.; Wielicki, B.A.; Doelling, D.R.; Smith, G.L.; Keyes, D.F.; Kato, S.; Manalo-Smith, N.; Wong, T. Toward optimal closure of the Earth’s top-of-atmosphere radiation budget. J. Clim. 2009, 22, 748–766. [Google Scholar] [CrossRef]
- Wild, M.; Folini, D.; Schär, C.; Loeb, N.; Dutton, E.G.; König-Langlo, G. The global energy balance from a surface perspective. Clim. Dyn. 2013, 40, 3107–3134. [Google Scholar] [CrossRef]
- Jakob Themeßl, M.; Gobiet, A.; Leuprecht, A. Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An introduction to Himawari-8/9-Japan’s new-generation geostationary meteorological satellites. J. Meteorol. Soc. Jpn. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Park, J.H.; Bok, J.Y.; Han-Oh, H.S.L.; Chung, D.W. Development of Radiometric Calibration System for GEO-KOMPSAT-2 AMI. In Proceedings of the SpaceOps 2016 Conference, Daejeon, Korea, 16–20 May 2016; Available online: https://doi.org/10.2514/6.2016-2325 (accessed on 1 February 2018).
- Murata, H.; Takahashi, M.; Kosaka, Y. VIS and IR bands of Himawari-8/AHI compatible with those of MTSAT-2/Imager. MSC Tech. Note 2015, 60, 1–18. [Google Scholar]
- Cullen, M.J.P. The unified forecast/climate model. Meteorol. Mag. 1993, 122, 81–94. [Google Scholar]
- Berrisford, P.; Dee, D.P.; Poli, P.; Brugge, R.; Fielding, K.; Fuentes, M.; Kållberg, P.W.; Kobayashi, S.; Uppala, S.; Simmons, A. The ERA-Interim Archive Version 2.0; ERA Report Series 1; ECMWF: Reading, UK, 2011. [Google Scholar]
- KMA. Climatological Normal of Korea (1981–2010). 2011. Available online: http://www.weather.go.kr/down/Climatological_2010.pdf (accessed on 21 June 2018).
- KMA. Annual Climatological Report (2016). 2016. Available online: http://www.weather.go.kr/repositary/sfc/pdf/sfc_ann_2016.pdf (accessed on 21 June 2018).
- NASA. CERES SYN1deg Ed3A Data Quality Summary. 2013. Available online: https://ceres.larc.nasa.gov/documents/DQ_summaries/CERES_SYN1deg_Ed3A_DQS.pdf (accessed on 1 February 2018).
- Loeb, N.G.; Lyman, J.M.; Johnson, G.C.; Allan, R.P.; Doelling, D.R.; Wong, T.; Soden, B.J.; Stephens, G.L. Observed changes in top-of-the-atmosphere radiation and upper-ocean heating consistent within uncertainty. Nat. Geosci. 2012, 5. [Google Scholar] [CrossRef]
- NASA. CERES EBAF Ed4.0 Data Quality Summary. 2017. Available online: https://ceres.larc.nasa.gov/documents/DQ_summaries/CERES_EBAF_Ed2.8_DQS.pdf (accessed on 1 February 2018).
- NASA. MERRA-2: File Specification. 2016. Available online: https://gmao.gsfc.nasa.gov/pubs/docs/Bosilovich785.pdf (accessed on 1 February 2018).
- NASA. MERRA-2 Input Observations: Summary and Assessment. 2016. Available online: https://gmao.gsfc.nasa.gov/pubs/docs/McCarty885.pdf (accessed on 1 February 2018).
- Bosilovich, M.G.; Robertson, F.R.; Chen, J. Global energy and water budgets in MERRA. J. Clim. 2011, 24, 5721–5739. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Dee, D.P.; Källén, E.; Simmons, A.J.; Haimberger, L. Comments on “Reanalyses suitable for characterizing long-term trends”. Bull. Am. Meteorol. Soc. 2011, 92, 65–70. [Google Scholar] [CrossRef]
- Spencer, J.W. Fourier series representation of the position of the sun. Search 1971, 2, 172. [Google Scholar]
- Prsa, A.; Harmanec, P.; Torres, G.; Mamajek, E.; Asplund, M.; Capitaine, N.; Christensen-Dalsgaard, J.; Depagne, E.; Haberreiter, M.; Hekker, S.; et al. Nominal values for selected solar and planetary quantities: IAU 2015 Resolution B3. Astron. J. 2016, 152. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, B.Y.; Lee, K.T.; Zo, I.S.; Jung, H.S.; Rim, S.H. Retrieval of reflected shortwave radiation at the top of the atmosphere using Himawari-8/AHI data. Remote Sens. 2018, 10, 213. [Google Scholar] [CrossRef]
- Loeb, N.G.; Hinton, P.O.R.; Green, R.N. Top-of-atmosphere albedo estimation from angular distribution models: A comparison between two approaches. J. Geophys. Res. Atmos. 1999, 104, 31255–31260. [Google Scholar] [CrossRef] [Green Version]
- Kato, S.; Marshak, A. Solar zenith and viewing geometry–dependent errors in satellite retrieved cloud optical thickness: Marine stratocumulus case. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Ricchiazzi, P.; Yang, S.; Gautier, C.; Sowle, D. SBDART: A research and teaching software tool for plane-parallel radiative transfer in the earth’s atmosphere. Bull. Am. Meteorol. Soc. 1998, 79, 2101–2114. [Google Scholar] [CrossRef]
- Clerbaux, N.; Dewitte, S.; Gonzalez, L.; Bertrand, C.; Nicula, B.; Ipe, A. Outgoing longwave flux estimation: Improvement of angular modelling using spectral information. Remote Sens. Environ. 2003, 85, 389–395. [Google Scholar] [CrossRef]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L.E. Estimation of the net radiation using MODIS (Moderate Resolution Imaging Spectroradiometer) data for clear sky days. Remote Sens. Environ. 2005, 97, 52–67. [Google Scholar] [CrossRef]
- Kato, S.; Loeb, N.G.; Rutan, D.A.; Rose, F.G.; Sun-Mack, S.; Miller, W.F.; Chen, Y. Uncertainty estimate of surface irradiances computed with MODIS-, CALIPSO-, and CloudSat-derived cloud and aerosol properties. Surv. Geophys. 2012, 33, 395–412. [Google Scholar] [CrossRef]
- Li, Z.Q.; Leighton, H.G.; Masuda, K.; Takashima, T. Estimation of SW flux absorbed at the surface from TOA reflected flux. J. Clim. 1993, 6, 317–330. [Google Scholar] [CrossRef]
- NOAA. GOES-R Advanced Baseline Imager (ABI) Algorithm Theoretical Basis Document for Absorbed Shortwave Radiation (Surface). 2010. Available online: http://www.goes-r.gov/products/ATBDs/option2/RB_ASR_v1.0_no_color.pdf (accessed on 1 February 2018).
- Ohring, G.; Gruber, A.; Ellingson, R. Satellite determinations of the relationship between total longwave radiation flux and infrared window radiance. J. Clim. Appl. Meteorol. 1984, 23, 416–425. [Google Scholar] [CrossRef]
- Abel, P.G.; Gruber, A. An improved model for the calculation of longwave flux at 11 μm. In NOAA Technical Memorandum NESS 106; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1979. [Google Scholar]
- Schmetz, J.; Liu, Q. Outgoing longwave radiation and its diurnal variation at regional scales derived from Meteosat. J. Geophys. Res. Atmos. 1988, 93, 11192–11204. [Google Scholar] [CrossRef]
- Otterman, J.; Starr, D.; Brakke, T.; Davies, R.; Jacobowitz, H.; Mehta, A.; Cheruy, F.; Prabhakara, C. Modeling zenith-angle dependence of outgoing longwave radiation: Implication for flux measurements. Remote Sens. Environ. 1997, 62, 90–100. [Google Scholar] [CrossRef]
- Kim, B.Y.; Lee, K.T.; Jee, J.B.; Zo, I.S. Retrieval of outgoing longwave radiation at top-of-atmosphere using Himawari-8 AHI data. Remote Sens. Environ. 2018, 204, 498–508. [Google Scholar] [CrossRef]
- Swinbank, W.C. Long-wave radiation from clear skies. Q. J. R. Meteorol. Soc. 1963, 89, 339–348. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D. Thermal radiation from the atmosphere. J. Geophys. Res. 1969, 74, 5397–5403. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History and Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Heitor, A.; Biga, A.J.; Rosa, R. Thermal radiation components of the energy balance at the ground. Agric. For. Meteorol. 1991, 54, 29–48. [Google Scholar] [CrossRef]
- Santos, C.A.C.D.; Silva, B.B.D.; Rao, T.V.R.; Satyamurty, P.; Manzi, A.O. Downward longwave radiation estimates for clear-sky conditions over northeast Brazil. Rev. Br. Meteorol. 2011, 26, 443–450. [Google Scholar] [CrossRef]
- Iziomon, M.G.; Mayer, H.; Matzarakis, A. Downward atmospheric longwave irradiance under clear and cloudy skies: Measurement and parameterization. J. Atmos. Sol. Terr. Phys. 2003, 65, 1107–1116. [Google Scholar] [CrossRef]
- Lee, H.T.; Laszlo, I.; Gruber, A. ABI earth radiation budget-downward longwave radiation: Surface (DLR). In NOAA Nesdis Center for Satellite Applications and Research Algorithm Theoretical Basis Document; National Oceanic and Atmospheric Administration: Washington, DC, USA, 2010. [Google Scholar]
- Sobrino, J.A.; El Kharraz, J.; Li, Z.L. Surface temperature and water vapour retrieval from MODIS data. Int. J. Remote Sens. 2003, 24, 5161–5182. [Google Scholar] [CrossRef]
- Jin, M.; Liang, S. An improved land surface emissivity parameter for land surface models using global remote sensing observations. J. Clim. 2006, 19, 2867–2881. [Google Scholar] [CrossRef]
- Doelling, D.R.; Loeb, N.G.; Keyes, D.F.; Nordeen, M.L.; Morstad, D.; Nguyen, C.; Wielicki, B.A.; Young, D.F.; Sun, M. Geostationary enhanced temporal interpolation for CERES flux products. J. Atmos. Ocean. Technol. 2013, 30, 1072–1090. [Google Scholar] [CrossRef]
- Doelling, D.R.; Sun, M.; Nguyen, L.T.; Nordeen, M.L.; Haney, C.O.; Keyes, D.F.; Mlynczak, P.E. Advances in geostationary-derived longwave fluxes for the CERES synoptic (SYN1deg) Product. J. Atmos. Ocean. Technol. 2016, 33, 503–521. [Google Scholar] [CrossRef]
- Yu, L.; Weller, R.A. Objectively analyzed air-sea heat fluxes for the global ice-free oceans (1981–2005). Bull. Am. Meteorol. Soc. 2007, 88, 527–539. [Google Scholar] [CrossRef]
- Roberts, J.B.; Clayson, C.A.; Robertson, F.R.; Jackson, D.L. Predicting near-surface atmospheric variables from Special Sensor Microwave/Imager using neural networks with a first-guess approach. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Garratt, J.R. The atmospheric boundary layer. Earth Sci. Rev. 1994, 37, 89–134. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology (Vol. 13); Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Hansen, J.; Nazarenko, L.; Ruedy, R.; Sato, M.; Willis, J.; Del Genio, A.; Koch, D.; Lacis, A.; Lo, K.; Menon, S.; et al. Earth’s energy imbalance: Confirmation and implications. Science 2005, 308, 1431–1435. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Ramanathan, V. Solar radiation budget and radiative forcing due to aerosols and clouds. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Zo, I.S.; Jee, J.B.; Kim, B.Y.; Lee, K.T. Baseline Surface Radiation Network (BSRN) quality control of solar radiation data on the Gangneung-Wonju National University radiation station. Asia Pac. J. Atmos. Sci. 2017, 53, 11–19. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Kharecha, P.; Schuckmann, K.V. Earth’s energy imbalance and implications. Atmos. Chem. Phys. 2011, 11, 13421–13449. [Google Scholar] [CrossRef] [Green Version]
- Trenberth, K.E. An imperative for climate change planning: Tracking Earth’s global energy. Curr. Opin. Environ. Sustain. 2009, 1, 19–27. [Google Scholar] [CrossRef]
- Fasullo, J.T.; Trenberth, K.E. The annual cycle of the energy budget. Part II: Meridional structures and poleward transports. J. Clim. 2008, 21, 2313–2325. [Google Scholar] [CrossRef]
- Yu, L. Global variations in oceanic evaporation (1958–2005): The role of the changing wind speed. J. Clim. 2007, 20, 5376–5390. [Google Scholar] [CrossRef]
- Fasullo, J.T.; Trenberth, K.E. The annual cycle of the energy budget. Part I: Global mean and land-ocean exchanges. J. Clim. 2008, 21, 2297–2312. [Google Scholar] [CrossRef]
- Inagaki, A.; Letzel, M.O.; Raasch, S.; Kanda, M. Impact of surface heterogeneity on energy imbalance: A study using LES. J. Meteorol. Soc. Jpn. Ser. II 2006, 84, 187–198. [Google Scholar] [CrossRef]
- Shepherd, J.M.; Pierce, H.; Negri, A.J. Rainfall modification by major urban areas: Observations from spaceborne rain radar on the TRMM satellite. J. Appl. Meteorol. 2002, 41, 689–701. [Google Scholar] [CrossRef]
- Zehnder, J.A. Simple modifications to improve fifth-generation Pennsylvania State University-National Center for Atmospheric Research mesoscale model performance for the Phoenix, Arizona, metropolitan area. J. Appl. Meteorol. 2002, 41, 971–979. [Google Scholar] [CrossRef]






















| Parameter | Values | N |
|---|---|---|
| Spectral Band (μm) | 0.41–0.51, 0.47–0.55, 0.56–0.71, 0.81–0.91, 1.55–1.67, 2.19–2.32, 0.2–3.3 | 7 |
| Atmospheric Profile | Tropical, Mid-Latitude Summer & Winter, Sub-Arctic Summer & Winter, US Standard | 6 |
| SZA (°) | 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85 | 18 |
| RAA (°) | 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180 | 19 |
| Aerosol Optical Thickness (AOT) | Rural, Urban, Oceanic, Tropospheric: VIS 1, 5, 10, 15, 20 km | 20 |
| Cloud Optical Thickness (COT) | 2, 4, 8, 16, 32, 64, 128 | 7 |
| Cloud Height (km) | 2, 4, 6, 8, 10, 12, 14, 16 | 8 |
| Surface Albedo | 0.0, 1.0, Water (spectral range mean: 0.04), Vegetation (0.28), Sand (0.32), Snow (0.43) | 6 |
| Parameter | Values | N |
|---|---|---|
| Spectral Band (μm) | 0.2–3.3 | 1 |
| Atmospheric Profile | Tropical, Mid-Latitude Summer & Winter, Sub-Arctic Summer & Winter, US Standard | 6 |
| CSZA | 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0 | 10 |
| TPW (cm) | 0.2, 0.4, 0.8, 1.6, 3.2, 6.4 | 6 |
| AOT | Rural, Urban, Oceanic, Tropospheric: 0.02, 0.04, 0.08, 0.16, 0.32, 0.64, 1.28 | 28 |
| COT | 2, 4, 8, 16, 32, 64, 128 | 7 |
| Cloud Height (km) | 2, 4, 6, 8, 10, 12, 14, 16 | 8 |
| Cloud Effective Radius (μm) | Water Cloud: 8, 16, 32, 64 Ice Cloud: 16, 32, 64, 128 | 8 |
| Surface Albedo | 0.0, 1.0, Water (0.04), Vegetation (0.28), Sand (0.32), Snow (0.43) | 6 |
| DSR | ||||||
| ASR | ||||||
| Parameter | Values | N |
|---|---|---|
| Spectral Band (μm) | 5.44–7.03, 11.18–13.65, 3.3–100 | 3 |
| Atmospheric Profile | Tropical, Mid-Latitude Summer & Winter, Sub-Arctic Summer & Winter, US Standard | 6 |
| SZA (°) | 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85 | 18 |
| COT | 2, 4, 8, 16, 32, 64, 128 | 7 |
| Cloud Height (km) | 0, 2, 4, 6, 8, 10, 12, 14, 16 | 9 |
| Temperature, H2O, CO2, O3, etc. | Default |
| Channel | ||||||
|---|---|---|---|---|---|---|
| 8 | ||||||
| 15 |
| Shortwave Radiation (RSR, DSR, ASR) | Longwave Radiation (OLR, DLR, ULR) | |||
|---|---|---|---|---|
| Month | Day | Time | Day | Time |
| 1 | 4, 20 | 0230 UTC | 4, 20 | 0230, 1330 UTC |
| 2 | 5, - | 5, - | ||
| 3 | 8, 24 | 8, 24 | ||
| 4 | 2, - | 2, 18 | ||
| 5 | 4, 20 | 4, 20 | ||
| 6 | 5, - | 5, 21 | ||
| 7 | 7, 23 | 7, 23 | ||
| 8 | 6, 22 | 6, 22 | ||
| 9 | 7, 23 | 7, 23 | ||
| 10 | 2, 18 | 2, 18 | ||
| 11 | 3, 19 | 3, 19 | ||
| 12 | 5, 21 | 5 *, 21 | ||
| CERES Mean | Bias | RMSE | R | |
|---|---|---|---|---|
| ISR | ||||
| RSR | ||||
| DSR | ||||
| ASR | ||||
| OLR | ||||
| DLR | ||||
| ULR |
| Observation Mean | Bias | RMSE | R | ||
|---|---|---|---|---|---|
| DSR | CERES | ||||
| Calculation | |||||
| DLR | CERES | ||||
| Calculation |
| Korean Peninsula | Metropolitan | Yeongdong | Island | |
|---|---|---|---|---|
(Seoul: ) | (Sokcho: ) | |||
(Seoul: ) | (Sokcho: ) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, B.-Y.; Lee, K.-T. Radiation Component Calculation and Energy Budget Analysis for the Korean Peninsula Region. Remote Sens. 2018, 10, 1147. https://doi.org/10.3390/rs10071147
Kim B-Y, Lee K-T. Radiation Component Calculation and Energy Budget Analysis for the Korean Peninsula Region. Remote Sensing. 2018; 10(7):1147. https://doi.org/10.3390/rs10071147
Chicago/Turabian StyleKim, Bu-Yo, and Kyu-Tae Lee. 2018. "Radiation Component Calculation and Energy Budget Analysis for the Korean Peninsula Region" Remote Sensing 10, no. 7: 1147. https://doi.org/10.3390/rs10071147
APA StyleKim, B. -Y., & Lee, K. -T. (2018). Radiation Component Calculation and Energy Budget Analysis for the Korean Peninsula Region. Remote Sensing, 10(7), 1147. https://doi.org/10.3390/rs10071147