GRACE-Based Terrestrial Water Storage in Northwest China: Changes and Causes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection
2.3. Data Processing
- (i)
- Connect the meteorological stations in NWC with straight lines, creating a Delaunay triangulation.
- (ii)
- Determine three perpendicular bisectors and a circumcenter for each triangle in the Delaunay triangulation, thus forming many polygons which take perpendicular bisectors and/or the outline of NWC as boundaries.
- (iii)
- Each polygon is controlled by one meteorological station, where the measured climatic factor values represent those over the whole polygon.
- (iv)
- Calculate the climatic factor values over a province according to Equation (6).
2.4. Cross-Wavelet Transformation
2.5. Pearson Correlation Coefficient Test
3. Results and Discussion
3.1. Data Weights of the Three Centers
3.2. TWS Variations in the NWC
3.3. Correlations between TWS and Climatic and Vegetational Factors
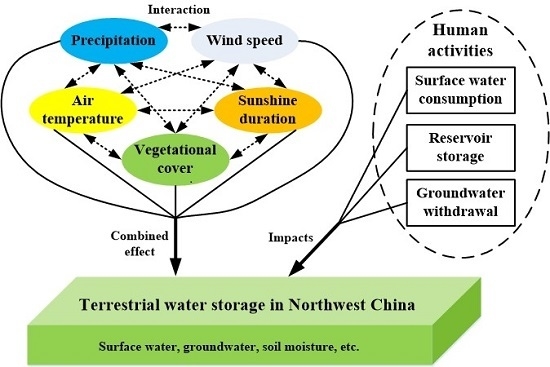
3.4. Effects of Climate and Vegetation Changes on TWS Variations
3.5. Connections between TWS Variations and Socioeconomic Water Consumption
4. Conclusions
- (1)
- TWS showed distinct seasonal variations and a significant decreasing tendency in NWC as a whole. In particular, TWS obviously decreased in the Shaanxi, Ningxia, Gansu, and Xinjiang provinces, while TWS notably increased in the Qinghai province. Increases in AT and NDVI were the main causes of the decreases in TWS in the Shaanxi, Ningxia, and Gansu provinces. The decreases in SD and WS resulted in an increase in TWS in the Qinghai province, while the decrease in TWS was caused by the obvious increase in AT in the Xinjiang province.
- (2)
- The interactions of climatic and vegetational factors were significant, and strong effects of some factors could weaken the influences of other factors on TWS variations in NWC. In particular, the negative effects of SD, AT, and NDVI jointly masked the positive effects of P and WS on TWS in the Xinjiang province, whereas the positive effect of P masked the negative effects of the other factors on TWS in the other provinces in NWC. Accordingly, we should emphasize the analysis of the interactions and combined effects of multiple effects on TWS variations in a region.
- (3)
- TWS in the Shaanxi, Ningxia, Gansu, and Qinghai provinces had good correlations with the variation in water storage in the cascade reservoirs of the upstream of the Yellow River, and the correlation coefficients gradually decreased from east to west in NWC. In addition, increasing AT could promote actual Et when more groundwater is converted into surface water in irrigated areas, thus resulting in a further reduction in TWS in NWC.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Famiglietti, J.S. Remote sensing of terrestrial water storage, soil moisture and surface waters. State Planet Front. Chall. Geophys. 2004, 150, 197–207. [Google Scholar]
- Tangdamrongsub, N.; Steele-Dunne, S.C.; Gunter, B.C.; Ditmar, P.G.; Weerts, A.H. Data assimilation of GRACE terrestrial water storage estimates into a regional hydrological model of the Rhine River basin. Hydrol. Earth Syst. Sci. 2015, 19, 2079–2100. [Google Scholar] [CrossRef] [Green Version]
- Deng, H.; Chen, Y. Influences of recent climate change and human activities on water storage variations in Central Asia. J. Hydrol. 2017, 544, 46–57. [Google Scholar] [CrossRef]
- Bhatti, A.M.; Koike, T.; Shrestha, M. Climate change impact assessment on mountain snow hydrology by water and energy budget—Based distributed hydrological model. J. Hydrol. 2016, 543, 523–541. [Google Scholar] [CrossRef]
- Jakob, D.; Walland, D. Variability and long-term change in Australian temperature and precipitation extremes. Weather Clim. Extremes 2016, 14, 36–55. [Google Scholar] [CrossRef]
- Frappart, F.; Seoane, L.; Ramillien, G. Validation of GRACE-derived terrestrial water storage from a regional approach over South America. Remote Sens. Environ. 2013, 137, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Hassan, A.; Jin, S. Water storage changes and balances in Africa observed by GRACE and hydrologic models. Geod. Geodyn. 2016, 7, 39–49. [Google Scholar] [CrossRef]
- Huang, P.; Li, Z.; Chen, J.; Li, Q.; Yao, C. Event-based hydrological modeling for detecting dominant hydrological process and suitable model strategy for semi-arid catchments. J. Hydrol. 2016, 542, 292–303. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Cazenave, A.; Güntner, A. Time variations of land water storage from an inversion of 2 years of GRACE geoids. Earth Planet. Sci. Lett. 2005, 235, 283–301. [Google Scholar] [CrossRef] [Green Version]
- Lenk, O. Satellite based estimates of terrestrial water storage variations in Turkey. J. Geodyn. 2013, 67, 106–110. [Google Scholar] [CrossRef]
- Forootan, E.; Rietbroek, R.; Kusche, J.; Sharifi, M.A.; Awang, J.; Schmidt, M.; Omondi, P.; Famiglietti, J. Separation of large scale water storage patterns over Iran using GRACE, altimetry and hydrological data. Remote Sens. Environ. 2014, 140, 580–595. [Google Scholar] [CrossRef] [Green Version]
- Yang, P.; Chen, Y. An analysis of terrestrial water storage variations from GRACE and GLDAS: The Tianshan Mountains and its adjacent areas, central Asia. Quat. Int. 2015, 358, 106–112. [Google Scholar] [CrossRef]
- Seyoum, W.M.; Milewski, A.M. Monitoring and comparison of terrestrial water storage changes in the northern high plains using GRACE and in-situ based integrated hydrologic model estimates. Adv. Water Resour. 2016, 94, 31–44. [Google Scholar] [CrossRef]
- Abiy, A.Z.; Melesse, A.M. Evaluation of watershed scale changes in groundwater and soil moisture storage with the application of GRACE satellite imagery data. Catena 2017, 153, 50–60. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M.; Zaitchik, B.F.; Reichle, R.H.; Koster, R.D.; van Dam, T.M. Assimilation of GRACE terrestrial water storage into a land surface model: Evaluation and potential value for drought monitoring in western and central Europe. J. Hydrol. 2012, 446–447, 103–115. [Google Scholar] [CrossRef]
- Zhou, Y.; Jin, S.; Tenzer, R.; Feng, J. Water storage variations in the Poyang Lake Basin estimated from GRACE and satellite altimetry. Geod. Geodyn. 2016, 7, 108–116. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Fang, W.; Huang, S.Z.; Huang, Q.; Huang, G.H.; Meng, E.H.; Luan, J.K. Reference evapotranspiration forecasting based on local meteorological and global climate information screened by partial mutual information. J. Hydrol. 2018, 561, 764–779. [Google Scholar] [CrossRef]
- Wang, Y.L.; Wang, X.; Zheng, Q.Y.; Li, C.H.; Guo, X.J. A comparative study on hourly real evapotranspiration and potential evapotranspiration during different vegetation growth stages in the Zoige Wetland. Procedia Environ. Sci. 2012, 13, 1585–1594. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, W.; Zhong, M.; Lemoine, J.M.; Biancale, R.; Hsu, H.T.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef] [Green Version]
- Haddad, O.B.; Moravej, M.; Loáiciga, H.A. Application of the water cycle algorithm to the optimal operation of reservoir systems. J. Irrig. Drain. Eng. 2014, 141, 04014064. [Google Scholar] [CrossRef]
- Huang, S.Z.; Chang, J.X.; Huang, Q.; Chen, Y.T. Spatio-temporal changes and frequency analysis of drought in the Wei River Basin, China. Water Resour. Manag. 2014, 28, 3095–3110. [Google Scholar] [CrossRef]
- Huang, S.Z.; Chang, J.X.; Huang, Q.; Chen, Y.T. Monthly streamflow prediction using modified EMD-based support vector machine. J. Hydrol. 2014, 511, 764–775. [Google Scholar] [CrossRef]
- Huang, S.Z.; Huang, Q.; Chang, J.X.; Leng, G.Y. Linkages between hydrological drought, climate indices and human activities: A case study in the Columbia River basin. Int. J. Climatol. 2016, 36, 280–290. [Google Scholar] [CrossRef]
- Huang, Y. Understanding China’s Belt and Road Initiative: Motivation, framework and assessment. China Econ. Rev. 2016, 40, 314–321. [Google Scholar] [CrossRef]
- Pan, C.J. Status and management of land desertification in Xinjiang Province. Mod. Hortic. 2018, 41, 179–180. (In Chinese) [Google Scholar]
- Fang, W.; Huang, Q.; Huang, S.Z.; Yang, J.; Meng, E.H.; Li, Y.Y. Optimal sizing of utility-scale photovoltaic power generation complementarily operating with hydropower: A case study of the world’s largest hydro-photovoltaic plant. Energy Convers. Manag. 2017, 136, 161–172. [Google Scholar] [CrossRef]
- Sakumura, C.; Bettadpur, S.; Bruinsma, S. Ensemble prediction and intercomparison analysis of GRACE time-variable gravity field models. Geophys. Res. Lett. 2014, 41, 1389–1397. [Google Scholar] [CrossRef] [Green Version]
- Famiglietti, J.; Lo, M.; Ho, S.; Bethune, J.; Anderson, K.; Syed, T.; Swenson, S.; de Linage, C.; Rodell, M. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38, L03403–L03406. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Faunt, C.C.; Longuevergne, L.; Reedy, R.C.; Alley, W.M.; McGuire, V.L.; McMahon, P.B. Groundwater depletion and sustainability of irrigation in the US High Plains and Central Valley. Proc. Natl. Acad. Sci. USA 2012, 109, 9320–9325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swenson, S.; Wahr, J. Methods for inferring regional surface-mass anomalies from Gravity Recovery and Climate Experiment (GRACE) measurements of time-variable gravity. J. Geophys. Res. Atmos. 2002, 107, 389–392. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Chen, J.L.; Rodell, M.; Wilson, C.R.; Famiglietti, J.S. Low degree spherical harmonic influences on Gravity Recovery and Climate Experiment (GRACE) water storage estimates. Geophys. Res. Lett. 2005, 32, 57–76. [Google Scholar] [CrossRef]
- Werth, S.; Güntner, A.; Schmidt, R.; Kusche, J. Evaluation of GRACE filter tools from a hydrological perspective. Geophys. J. R. Astron. Soc. 2010, 179, 1499–1515. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Ries, J.C. Low degree gravitational changes from GRACE: Validation and interpretation. Geophys. Res. Lett. 2004, 31, 359–393. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D. Variations in the Earth’s oblateness during the past 28 years. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Yang, Z.L.; Niu, G.Y. 2005 drought event in the Amazon River basin as measured by GRACE and estimated by climate models. J. Geophys. Res. Atmos. 2009, 114, B05404. [Google Scholar] [CrossRef]
- Zhou, H.; Deng, Z.; Xia, Y.; Fu, M. A new sampling method in particle filter based on Pearson correlation coefficient. Neurocomputing 2016, 216, 208–215. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Güntner, A.; Ngo-Duc, T.; Cazenave, A.; Laval, K. Time variations of the regional evapotranspiration rate from Gravity Recovery and Climate Experiment (GRACE) satellite gravimetry. Water Resour. Res. 2006, 42, 10403. [Google Scholar] [CrossRef]
- Croley, T.E., II; Hartmann, H.C. Resolving Thiessen polygons. J. Hydrol. 1985, 76, 363–379. [Google Scholar] [CrossRef]
- Bai, J.J.; Bai, J.T.; Wang, L. Spatio-temporal change of vegetation NDVI and its relations with regional climate in Northern Shannxi Province in 2000–2010. Sci. Geogr. Sin. 2014, 34, 882–888. (In Chinese) [Google Scholar]
- Hudgins, L.; Huang, J.P. Bivariate Wavelet Analysis of Asia Monsoon and ENSO. Adv. Atmos. Sci. 1996, 13, 299–312. [Google Scholar] [CrossRef]
- Huang, S.; Huang, Q.; Leng, G.; Meng, E.H. Variations in annual water-energy balance and their correlations with vegetation and soil moisture dynamics: A case study in the Wei River Basin, China. J. Hydrol. 2017, 546, 515–525. [Google Scholar] [CrossRef]
- Niu, J.; Sivakumar, B. Scale-dependent synthetic streamflow generation using a continuous wavelet transform. J. Hydrol. 2013, 496, 71–78. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef] [Green Version]
- Ndehedehe, C.E.; Agutu, N.O.; Okwuashi, O.; Ferreira, V.G. Spatio-temporal variability of droughts and terrestrial water storage over Lake Chad Basin using independent component analysis. J. Hydrol. 2016, 540, 106–128. [Google Scholar] [CrossRef] [Green Version]
- Luo, Z.; Chen, Y.; Ning, J. Effect of Terrain on the Determination of High Precise Local Gravimetric Geoid. Edit. Board Geomat. Inf. Sci. Wuhan Univ. 2003, 28, 340–344. (In Chinese) [Google Scholar]
- Huang, S.; Hou, B.; Chang, J.; Huang, Q.; Chen, Y. Spatial-temporal change in precipitation patterns based on the cloud model across the Wei River Basin, China. Theor. Appl. Climatol. 2015, 120, 391–401. [Google Scholar] [CrossRef]
- Kang, K.; Li, H.; Peng, P.; Zou, Z. Low-frequency variability of terrestrial water budget in China using GRACE satellite measurements from 2003 to 2010. Geod. Geodyn. 2015, 6, 444–452. [Google Scholar] [CrossRef]
- Yin, W.J.; Hu, L.T.; Wang, J.R. Changes of groundwater storage variation based on GRACE data at the Beishan area, Gansu province. Hydrogeol. Eng. Geol. 2015, 42, 29–34. (In Chinese) [Google Scholar]
- Zhao, Q.; Wu, W.; Wu, Y. Variations in China’s terrestrial water storage over the past decade using GRACE data. Geod. Geodyn. 2015, 6, 187–193. [Google Scholar] [CrossRef]
- Herrera, V.M.V.; Soon, W.; Herrera, G.V.; Traversi, R.; Horiuchi, K. Generalization of the cross-wavelet function. New Astron. 2017, 56, 86–93. [Google Scholar] [CrossRef]
- Li, Y.; Sun, C. Impacts of the superimposed climate trends on droughts over 1961–2013 in Xinjiang, China. Theor. Appl. Climatol. 2016, 129, 977–994. [Google Scholar] [CrossRef]
- Xu, W.; Gu, S.; Zhao, X.Q.; Xiao, J.S.; Tang, Y.H.; Fang, J.Y.; Zhang, J.; Jiang, S. High positive correlation between soil temperature and NDVI from 1982 to 2006 in alpine meadow of the Three-River Source Region on the Qinghai-Tibetan Plateau. Int. J. Appl. Earth Observ. Geoinf. 2011, 13, 528–535. [Google Scholar] [CrossRef]
- Kong, D.; Zhang, Q.; Singh, V.P.; Shi, P. Seasonal vegetation response to climate change in the northern hemisphere (1982–2013). Glob. Planet. Chang. 2017, 148, 1–8. [Google Scholar] [CrossRef]
- Gessner, U.; Naeimi, V.; Klein, I.; Kuenzer, C.; Klein, D.; Dech, S. The relationship between precipitation anomalies and satellite-derived vegetation activity in Central Asia. Glob. Planet. Chang. 2013, 110, 74–87. [Google Scholar] [CrossRef]
- Mcvicar, T.R.; Roderick, M.L.; Donohue, R.J.; Li, L.T.; Niel, T.G.V.; Thomas, A.; Grieser, J.; Jhajharia, D.; Himri, Y.; Mahowald, N.M.; et al. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416, 182–205. [Google Scholar] [CrossRef]
- Kousari, M.R.; Ahani, H.; Hakimelahi, H. An investigation of near surface wind speed trends in arid and semiarid regions of Iran. Theor. Appl. Climatol. 2013, 114, 153–168. [Google Scholar] [CrossRef]
- Dai, X.G.; Wang, P.; Zhang, K.J. A study on precipitation trend and fluctuation mechanism in northwestern China over the past 60 years. Acta Phys. Sin. 2013, 62, 129201. [Google Scholar] [CrossRef]
- Huang, W.; Chang, S.Q.; Xie, C.L.; Zhang, Z.P. Moisture sources of extreme summer precipitation events in North Xinjiang and their relationship with atmospheric circulation. Adv. Clim. Chang. Res. 2017, 8, 12–17. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, M.; Wang, S.; Qiang, F.; Zeng, T.; Ren, Z.; Dong, L. Comparison of monthly precipitation derived from high-resolution gridded datasets in arid Xinjiang, central Asia. Quat. Int. 2015, 358, 160–170. [Google Scholar] [CrossRef]
- Wang, W.; Feng, Q.S.; Guo, N.; Sha, S.; Hu, D.; Wang, L.J.; Li, Y.H. Dynamic monitoring of vegetation coverage based on long time-series NDVI data sets in northwest arid region of China. Pratac. Sci. 2015, 32, 1969–1979. (In Chinese) [Google Scholar]
- Yin, Y.H.; Wu, S.H.; Dai, E.F. Determining factors in potential evapotranspiration changes over China in the period 1971–2008. Sci. Bull. 2010, 55, 3329–3337. [Google Scholar] [CrossRef]
- Tang, X.L.; Lv, X.; He, Y. Features of climate change and their effects on glacier snow melting in Xinjiang, China. C. R. Geosci. 2013, 345, 93–100. [Google Scholar] [CrossRef]
- Yang, L.; Wei, W.; Chen, L.; Chen, W.; Wang, J. Response of temporal variation of soil moisture to vegetation restoration in semi-arid Loess Plateau, China. Catena 2014, 115, 123–133. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.W.; Deng, L.; Yan, W.M.; Shangguan, Z.P. Interaction of soil water storage dynamics and long-term natural vegetation succession on the Loess Plateau, China. Catena 2016, 137, 52–60. [Google Scholar] [CrossRef]
- Shen, Q.; Gao, G.; Fu, B.; Lü, Y. Responses of shelterbelt stand transpiration to drought and groundwater variations in an arid inland river basin of Northwest China. J. Hydrol. 2015, 531, 738–748. [Google Scholar] [CrossRef] [Green Version]
- Döll, P.; Dobrev, H.H.; Portmann, F.T.; Siebert, S.; Eicker, A.; Rodell, M.; Strassberg, G.; Scanlon, B.R. Impact of water withdrawals from groundwater and surface water on continental water storage variations. J. Geodyn. 2012, 59–60, 143–156. [Google Scholar] [CrossRef]
- Yeh, J.F.; Swenson, S.C.; Famiglietti, J.S.; Rodell, M. Remote sensing of groundwater storage changes in Illinois using the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2006, 42, 395–397. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Longuevergne, L.; Long, D. Ground referencing GRACE satellite estimates of groundwater storage changes in the California Central Valley, USA. Water Resour. Res. 2012, 48, 4520. [Google Scholar] [CrossRef]
- Döll, P.; Schmied, H.M.; Schuh, C.; Portmann, F.T.; Eicker, A. Global-scale assessment of groundwater depletion and related groundwater abstractions: Combining hydrological modeling with information from well observations and GRACE satellites. Water Resour. Res. 2015, 50, 5698–5720. [Google Scholar] [CrossRef]
- Bhanja, S.N.; Mukherjee, A.; Saha, D.; Velicogna, I.; Famiglietti, J.S. Validation of GRACE based groundwater storage anomaly using in-situ groundwater level measurements in India. J. Hydrol. 2016, 2016, 543. [Google Scholar] [CrossRef]
- Cui, Y.L.; Zhang, G.; Shao, J.L. Classification and Characteristics of Groundwater System in the Yellow River Basin. Resour. Sci. 2004, 26, 2–8. (In Chinese) [Google Scholar]
- Jing, J.; Sun, J.; Han, S.; Wang, S. Distribution of groundwater resources and the state of development and utilization in the northwestern area. South-to-North Water Transf. Water Sci. Technol. 2007, 5, 54–56. (In Chinese) [Google Scholar]
- Liu, X.; Shen, Y.; Guo, Y.; Li, S.; Guo, B. Modeling demand/supply of water resources in the arid region of northwestern China during the late 1980s to 2010. J. Geogr. Sci. 2015, 25, 573–591. [Google Scholar] [CrossRef]
- Hu, X.; Shi, L.; Zeng, J.; Yang, J.; Zha, Y.; Yao, Y.; Cao, G. Estimation of actual irrigation amount and its impact on groundwater depletion: A case study in the Hebei Plain, China. J. Hydrol. 2016, 543, 433–449. [Google Scholar] [CrossRef]
- Leng, G.; Tang, Q. Modeling the impacts of future climate change on irrigation over China: Sensitivity to adjusted projections. J. Hydrometeorol. 2014, 15, 2085–2103. [Google Scholar] [CrossRef]
- Leng, G.; Huang, M.; Tang, Q.; Gao, H.; Leung, L. Modeling the effects of groundwater-fed irrigation on terrestrial hydrology over the conterminous United States. J. Hydrometeorol. 2014, 15, 957–972. [Google Scholar] [CrossRef]
- Leng, G.; Huang, M.; Tang, Q.; Leung, L. A modeling study of irrigation effects on global surface water and groundwater resources under a changing climate. J. Adv. Model. Earth Syst. 2015, 7, 1285–1304. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Wei, X.; Jiang, Y.; Feng, D. Response of groundwater cycle to environmental changes in Guanzhong Plain irrigation district. Trans. Chin. Soc. Agric. Eng. 2014, 30, 123–131. (In Chinese) [Google Scholar]
- Zhang, X.; Zhang, L.; He, C.; Li, J.; Jiang, Y.; Ma, L. Quantifying the impacts of land use/land cover change on groundwater depletion in Northwestern China-A case study of the Dunhuang oasis. Agric. Water Manag. 2014, 146, 270–279. [Google Scholar] [CrossRef]









| Province | CSR | GFZ | JPL |
|---|---|---|---|
| Shaanxi | 0.335 | 0.333 | 0.333 |
| Ningxia | 0.335 | 0.334 | 0.331 |
| Gansu | 0.337 | 0.332 | 0.331 |
| Qinghai | 0.341 | 0.332 | 0.327 |
| Xinjiang | 0.344 | 0.331 | 0.326 |
| Factors in Pair | PCC | Shaanxi | Ningxia | Gansu | Qinghai | Xinjiang |
|---|---|---|---|---|---|---|
| P and SD | r | 0.10 | 0.26 | 0.33 | 0.07 | 0.60 |
| r’ | −0.60 | −0.50 | −0.55 | −0.77 | −0.60 | |
| P and AT | r | 0.77 | 0.73 | 0.83 | 0.89 | 0.72 |
| r’ | −0.33 | −0.26 | −0.29 | −0.12 | −0.21 | |
| P and WS | r | −0.18 | 0.06 | 0.01 | 0.04 | 0.55 |
| r’ | −0.29 | −0.13 | −0.09 | −0.09 | 0.23 | |
| P and NDVI | r | 0.77 | 0.78 | 0.87 | 0.90 | 0.74 |
| r’ | −0.19 | −0.20 | −0.21 | −0.34 | −0.14 | |
| SD and AT | r | 0.56 | 0.66 | 0.65 | 0.36 | 0.94 |
| r’ | 0.45 | 0.32 | 0.39 | 0.17 | 0.26 | |
| SD and WS | r | 0.48 | 0.34 | 0.32 | 0.24 | 0.76 |
| r’ | 0.36 | 0.05 | 0.03 | 0.14 | −0.36 | |
| SD and NDVI | r | 0.50 | 0.51 | 0.54 | 0.19 | 0.84 |
| r’ | 0.37 | 0.33 | 0.40 | 0.45 | 0.28 | |
| AT and WS | r | 0.13 | 0.27 | 0.20 | 0.18 | 0.76 |
| r’ | 0.23 | 0.17 | 0.07 | 0.16 | −0.15 | |
| AT and NDVI | r | 0.94 | 0.87 | 0.91 | 0.86 | 0.89 |
| r’ | 0.12 | 0.10 | 0.15 | 0.19 | 0.10 | |
| WS and NDVI | r | −0.04 | 0.03 | −0.05 | −0.12 | 0.54 |
| r’ | 0.11 | 0.01 | 0.09 | 0.10 | −0.07 |
| Factors in Pair | PCC | Shaanxi | Ningxia | Gansu | Qinghai | Xinjiang |
|---|---|---|---|---|---|---|
| ΔTWS and P | r | 0.55 | 0.55 | 0.53 | 0.58 | −0.49 |
| r’ | 0.31 | 0.37 | 0.32 | 0.31 | 0.11 | |
| ΔTWS and SD | r | 0.20 | 0.22 | 0.38 | 0.09 | −0.71 |
| r’ | −0.31 | −0.30 | −0.15 | −0.17 | −0.14 | |
| ΔTWS and AT | r | 0.55 | 0.46 | 0.51 | 0.50 | −0.74 |
| r’ | −0.18 | −0.19 | −0.16 | −0.16 | −0.13 | |
| ΔTWS and WS | r | 0.13 | 0.24 | 0.31 | 0.31 | −0.45 |
| r’ | −0.14 | −0.07 | −0.11 | −0.18 | 0.10 | |
| ΔTWS and NDVI | r | 0.52 | 0.50 | 0.52 | 0.48 | −0.77 |
| r’ | −0.29 | −0.17 | −0.28 | −0.26 | −0.11 |
| Climatic and Vegetational Factors | Shaanxi | Ningxia | Gansu | Qinghai | Xinjiang |
|---|---|---|---|---|---|
| P | +1 * | +1 * | +1 * | +1 * | +4↑ |
| SD | −2 * | −2 * | −4 * | −4↓ | −1 * |
| AT | −4↑ | −3↑ | −3↑ | −5↑ | −2↑ |
| WS | −5 * | −5 * | −5 * | −3↓ | +5 * |
| NDVI | −3↑ | −4↑ | −2↑ | −2 * | −3 * |
| Province | Shaanxi | Ningxia | Gansu | Qinghai |
|---|---|---|---|---|
| r’ | 0.40 | 0.37 | 0.33 | 0.16 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Huang, S.; Liu, S.; Leng, G.; Peng, J.; Huang, Q.; Li, P. GRACE-Based Terrestrial Water Storage in Northwest China: Changes and Causes. Remote Sens. 2018, 10, 1163. https://doi.org/10.3390/rs10071163
Xie Y, Huang S, Liu S, Leng G, Peng J, Huang Q, Li P. GRACE-Based Terrestrial Water Storage in Northwest China: Changes and Causes. Remote Sensing. 2018; 10(7):1163. https://doi.org/10.3390/rs10071163
Chicago/Turabian StyleXie, Yangyang, Shengzhi Huang, Saiyan Liu, Guoyong Leng, Jian Peng, Qiang Huang, and Pei Li. 2018. "GRACE-Based Terrestrial Water Storage in Northwest China: Changes and Causes" Remote Sensing 10, no. 7: 1163. https://doi.org/10.3390/rs10071163
APA StyleXie, Y., Huang, S., Liu, S., Leng, G., Peng, J., Huang, Q., & Li, P. (2018). GRACE-Based Terrestrial Water Storage in Northwest China: Changes and Causes. Remote Sensing, 10(7), 1163. https://doi.org/10.3390/rs10071163