Urban Change Detection Based on Dempster–Shafer Theory for Multitemporal Very High-Resolution Imagery
Abstract
:1. Introduction
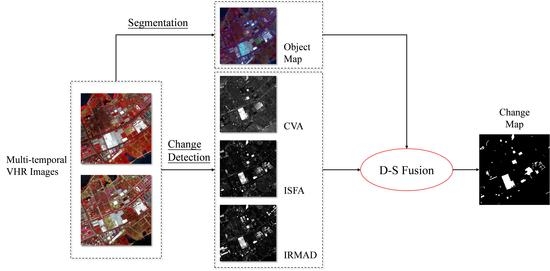
2. Methodology
- (1)
- Obtain the object map by the segmentation of stacked multitemporal VHR images;
- (2)
- Implement three change detection methods (CVA, ISFA, and IRMAD) to get change intensity, and utilize OTSU thresholding method to obtain the candidate change maps;
- (3)
- Fuse the three candidate change maps by the object map and D–S theory to obtain the final object-oriented change map.
2.1. Segmentation
2.2. Change Detection
2.3. Fusion with D–S Theory
3. Experiment
3.1. First Dataset
3.2. Second Dataset
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, F.; Li, X. Optimal clustering framework for hyperspectral band selection. IEEE Trans. Geosci. Remote Sens. 2018, 1–13. [Google Scholar] [CrossRef]
- Wang, Q.; Meng, Z.; Li, X. Locality adaptive discriminant analysis for spectral-spatial classification of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2077–2081. [Google Scholar] [CrossRef]
- Fan, C.; Wang, L.; Liu, P.; Lu, K.; Liu, D. Compressed sensing based remote sensing image reconstruction via employing similarities of reference images. Multimed. Tools Appl. 2016, 75, 12201–12225. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, J.; Liu, P.; Choo, K.-K.R.; Huang, F. Spectral–spatial multi-feature-based deep learning for hyperspectral remote sensing image classification. Soft Comput. 2017, 21, 213–221. [Google Scholar] [CrossRef]
- Dou, M.; Chen, J.; Chen, D.; Chen, X.; Deng, Z.; Zhang, X.; Xu, K.; Wang, J. Modeling and simulation for natural disaster contingency planning driven by high-resolution remote sensing images. Future Gener. Comput. Syst. 2014, 37, 367–377. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Coppin, P.; Jonckheere, I.; Nackaerts, K.; Muys, B.; Lambin, E. Digital change detection methods in ecosystem monitoring: A review. Int. J. Remote Sens. 2004, 25, 1565–1596. [Google Scholar] [CrossRef]
- Singh, A. Review article digital change detection techniques using remotely-sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y. Remote sensing research issues of the national land use change program of china. ISPRS J. Photogramm. 2007, 62, 461–472. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Townsend, P.A.; Gross, J.E.; Cohen, W.B.; Bolstad, P.; Wang, Y.Q.; Adams, P. Remote sensing change detection tools for natural resource managers: Understanding concepts and tradeoffs in the design of landscape monitoring projects. Remote Sens. Environ. 2009, 113, 1382–1396. [Google Scholar] [CrossRef]
- Li, H.; Xiao, P.; Feng, X.; Yang, Y.; Wang, L.; Zhang, W.; Wang, X.; Feng, W.; Chang, X. Using land long-term data records to map land cover changes in china over 1981–2010. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1372–1389. [Google Scholar] [CrossRef]
- Li, Z.; Shi, W.; Myint, S.W.; Lu, P.; Wang, Q. Semi-automated landslide inventory mapping from bitemporal aerial photographs using change detection and level set method. Remote Sens. Environ. 2016, 175, 215–230. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Ke, L.; Richards, K.S. Remote sensing of alpine lake water environment changes on the tibetan plateau and surroundings: A review. ISPRS J. Photogramm. 2014, 92, 26–37. [Google Scholar] [CrossRef]
- Xian, G.; Homer, C.; Fry, J. Updating the 2001 national land cover database land cover classification to 2006 by using landsat imagery change detection methods. Remote Sens. Environ. 2009, 113, 1133–1147. [Google Scholar] [CrossRef]
- Vittek, M.; Brink, A.; Donnay, F.; Simonetti, D.; Desclée, B. Land cover change monitoring using landsat mss/tm satellite image data over west africa between 1975 and 1990. Remote Sens. 2014, 6, 658–676. [Google Scholar] [CrossRef] [Green Version]
- Araya, Y.H.; Cabral, P. Analysis and modeling of urban land cover change in setúbal and sesimbra, portugal. Remote Sens. 2010, 2, 1549–1563. [Google Scholar] [CrossRef]
- Rokni, K.; Ahmad, A.; Selamat, A.; Hazini, S. Water feature extraction and change detection using multitemporal landsat imagery. Remote Sens. 2014, 6, 4173–4189. [Google Scholar] [CrossRef]
- Hussain, M.; Chen, D.; Cheng, A.; Wei, H.; Stanley, D. Change detection from remotely sensed images: From pixel-based to object-based approaches. ISPRS J. Photogramm. 2013, 80, 91–106. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L. A theoretical framework for unsupervised change detection based on change vector analysis in the polar domain. IEEE Trans. Geosci. Remote Sens. 2007, 45, 218–236. [Google Scholar] [CrossRef]
- Ridd, M.K.; Liu, J. A comparison of four algorithms for change detection in an urban environment. Remote Sens. Environ. 1998, 63, 95–100. [Google Scholar] [CrossRef]
- Carvalho Júnior, O.A.; Guimarães, R.F.; Gillespie, A.R.; Silva, N.C.; Gomes, R.A.T. A new approach to change vector analysis using distance and similarity measures. Remote Sens. 2011, 3, 2473–2493. [Google Scholar] [CrossRef]
- Wu, C.; Du, B.; Zhang, L. Slow feature analysis for change detection in multispectral imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2858–2874. [Google Scholar] [CrossRef]
- Nielsen, A.A. The regularized iteratively reweighted mad method for change detection in multi- and hyperspectral data. IEEE Trans. Image Process. 2007, 16, 463–478. [Google Scholar] [CrossRef] [PubMed]
- Celik, T. Unsupervised change detection in satellite images using principal component analysis and k-means clustering. IEEE Geosci. Remote Sens. Lett. 2009, 6, 772–776. [Google Scholar] [CrossRef]
- Huang, Z.; Jia, X.P.; Ge, L.L. Sampling approaches for one-pass land-use/land-cover change mapping. Int. J. Remote Sens. 2010, 31, 1543–1554. [Google Scholar] [CrossRef]
- Yuan, F.; Sawaya, K.E.; Loeffelholz, B.C.; Bauer, M.E. Land cover classification and change analysis of the twin cities (minnesota) metropolitan area by multitemporal landsat remote sensing. Remote Sens. Environ. 2005, 98, 317–328. [Google Scholar] [CrossRef]
- Lei, Z.; Fang, T.; Huo, H.; Li, D. Bi-temporal texton forest for land cover transition detection on remotely sensed imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1227–1237. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, T.; Zhang, L.; Tang, Y. A novel building change index for automatic building change detection from high-resolution remote sensing imagery. Remote Sens. Lett. 2014, 5, 713–722. [Google Scholar] [CrossRef]
- Bruzzone, L.; Bovolo, F. A novel framework for the design of change-detection systems for very-high-resolution remote sensing images. Proc. IEEE 2013, 101, 609–630. [Google Scholar] [CrossRef]
- Brunner, D.; Lemoine, G.; Bruzzone, L. Earthquake damage assessment of buildings using vhr optical and sar imagery. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2403–2420. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, L. Urban change analysis with multi-sensor multispectral imagery. Remote Sens. 2017, 9, 252. [Google Scholar] [CrossRef]
- Sun, L.; Tang, Y.; Zhang, L. Rural building detection in high-resolution imagery based on a two-stage cnn model. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1998–2002. [Google Scholar] [CrossRef]
- Volpi, M.; Tuia, D.; Bovolo, F.; Kanevski, M.; Bruzzone, L. Supervised change detection in vhr images using contextual information and support vector machines. Int. J. Appl. Earth Obs. Geoinf. 2013, 20, 77–85. [Google Scholar] [CrossRef]
- Wang, Q.; Wan, J.; Yuan, Y. Locality constraint distance metric learning for traffic congestion detection. Pattern Recognit. 2018, 75, 272–281. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, J.; Yuan, Y. A joint convolutional neural networks and context transfer for street scenes labeling. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1457–1470. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, L.; Huang, X. Object-oriented change detection based on the kolmogorov–smirnov test using high-resolution multispectral imagery. Int. J. Remote Sens. 2011, 32, 5719–5740. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Blaschke, T.; Ma, X.; Tiede, D.; Cheng, L.; Chen, Z.; Chen, D. Object-based change detection in urban areas: The effects of segmentation strategy, scale, and feature space on unsupervised methods. Remote Sens. 2016, 8, 761. [Google Scholar] [CrossRef]
- Wen, D.; Huang, X.; Zhang, L.; Benediktsson, J.A. A novel automatic change detection method for urban high-resolution remotely sensed imagery based on multiindex scene representation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 609–625. [Google Scholar] [CrossRef]
- Gueguen, L.; Pesaresi, M.; Ehrlich, D.; Lu, L.; Guo, H. Urbanization detection by a region based mixed information change analysis between built-up indicators. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2410–2420. [Google Scholar] [CrossRef]
- Dutta, P. An uncertainty measure and fusion rule for conflict evidences of big data via dempster–shafer theory. Int. J. Image Data Fusion 2017, 1–18. [Google Scholar] [CrossRef]
- Hegarat-Mascle, S.L.; Bloch, I.; Vidal-Madjar, D. Application of dempster-shafer evidence theory to unsupervised classification in multisource remote sensing. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1018–1031. [Google Scholar] [CrossRef]
- Hao, M.; Shi, W.; Zhang, H.; Wang, Q.; Deng, K. A scale-driven change detection method incorporating uncertainty analysis for remote sensing images. Remote Sens. 2016, 8, 745. [Google Scholar] [CrossRef]
- Lu, Y.H.; Trinder, J.C.; Kubik, K. Automatic building detection using the dempster-shafer algorithm. Photogramm. Eng. Remote Sens. 2006, 72, 395–403. [Google Scholar] [CrossRef]
- Desclée, B.; Bogaert, P.; Defourny, P. Forest change detection by statistical object-based method. Remote Sens. Environ. 2006, 102, 1–11. [Google Scholar] [CrossRef]
- Marpu, P.R.; Gamba, P.; Canty, M.J. Improving change detection results of ir-mad by eliminating strong changes. IEEE Geosci. Remote Sens. Lett. 2011, 8, 799–803. [Google Scholar] [CrossRef]
- Canty, M.J.; Nielsen, A.A. Automatic radiometric normalization of multitemporal satellite imagery with the iteratively re-weighted mad transformation. Remote Sens. Environ. 2008, 112, 1025–1036. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, L.; Du, B. Kernel slow feature analysis for scene change detection. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2367–2384. [Google Scholar] [CrossRef]
- Wu, C.; Du, B.; Cui, X.; Zhang, L. A post-classification change detection method based on iterative slow feature analysis and bayesian soft fusion. Remote Sens. Environ. 2017, 199, 241–255. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D.F. Automatic analysis of the difference image for unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1171–1182. [Google Scholar] [CrossRef]
- Shafer, G. Dempster-shafer theory. Encycl. Artif. Intell. 1992, 330–331. [Google Scholar]
- Luo, H.; Wang, L.; Shao, Z.; Li, D. Development of a multi-scale object-based shadow detection method for high spatial resolution image. Remote Sens. Lett. 2015, 6, 59–68. [Google Scholar] [CrossRef]
- Luo, H.; Li, D.; Liu, C. Parameter evaluation and optimization for multi-resolution segmentation in object-based shadow detection using very high resolution imagery. Geocarto Int. 2017, 32, 1307–1332. [Google Scholar] [CrossRef]
















| Kappa | OA | DR | FAR | F1-Score | ||
|---|---|---|---|---|---|---|
| CVA | K-means | 0.8444 | 0.9757 | 0.9311 | 0.2051 | 0.8576 |
| EM | 0.7863 | 0.9640 | 0.9502 | 0.3007 | 0.8057 | |
| OTSU | 0.8444 | 0.9757 | 0.9312 | 0.2051 | 0.8576 | |
| Max | 0.8912 | 0.9846 | 0.8788 | 0.0786 | 0.8996 | |
| IRMAD | K-means | 0.8666 | 0.9814 | 0.8396 | 0.0829 | 0.8766 |
| EM | 0.5179 | 0.8837 | 0.9872 | 0.5976 | 0.5718 | |
| OTSU | 0.8680 | 0.9814 | 0.8504 | 0.0925 | 0.8780 | |
| Max | 0.8681 | 0.9815 | 0.8489 | 0.0906 | 0.8781 | |
| ISFA | K-means | 0.8615 | 0.9814 | 0.8044 | 0.0491 | 0.8715 |
| EM | 0.6109 | 0.9174 | 0.9833 | 0.5126 | 0.6518 | |
| OTSU | 0.8656 | 0.9818 | 0.8129 | 0.0517 | 0.8754 | |
| Max | 0.8884 | 0.9841 | 0.8831 | 0.0885 | 0.8970 |
| Kappa | OA | DR | FAR | F1-Score | |
|---|---|---|---|---|---|
| CVA | 0.8444 | 0.9757 | 0.9312 | 0.2051 | 0.8576 |
| IRMAD | 0.8680 | 0.9814 | 0.8504 | 0.0925 | 0.8780 |
| ISFA | 0.8656 | 0.9818 | 0.8129 | 0.0517 | 0.8754 |
| CVA_MajorVote | 0.9165 | 0.9879 | 0.9252 | 0.0790 | 0.9231 |
| IRMAD_MajorVote | 0.9002 | 0.9865 | 0.8408 | 0.0146 | 0.9074 |
| ISFA_MajorVote | 0.8849 | 0.9847 | 0.8136 | 0.0103 | 0.8930 |
| MajorVote_Fusion | 0.9004 | 0.9866 | 0.8378 | 0.0098 | 0.9076 |
| D–S_Fusion | 0.9327 | 0.9904 | 0.9240 | 0.0478 | 0.9379 |
| Kappa | OA | DR | FAR | F1-Score | ||
|---|---|---|---|---|---|---|
| CVA | K-means | 0.3474 | 0.8964 | 0.9433 | 0.7599 | 0.3828 |
| EM | 0.6869 | 0.9760 | 0.8179 | 0.3895 | 0.6991 | |
| OTSU | 0.7485 | 0.9833 | 0.7655 | 0.2510 | 0.7572 | |
| Max | 0.7687 | 0.9862 | 0.7017 | 0.1327 | 0.7758 | |
| IRMAD | K-means | 0.6933 | 0.9781 | 0.7682 | 0.3492 | 0.7046 |
| EM | 0.3943 | 0.9108 | 0.9741 | 0.7270 | 0.4265 | |
| OTSU | 0.6796 | 0.9818 | 0.5902 | 0.1736 | 0.6887 | |
| Max | 0.7018 | 0.9808 | 0.6959 | 0.2717 | 0.7117 | |
| ISFA | K-means | 0.6950 | 0.9779 | 0.7810 | 0.3551 | 0.7064 |
| EM | 0.3745 | 0.9036 | 0.9766 | 0.7420 | 0.4082 | |
| OTSU | 0.6811 | 0.9816 | 0.6007 | 0.1886 | 0.6903 | |
| Max | 0.7017 | 0.9813 | 0.6748 | 0.2480 | 0.7113 |
| Kappa | OA | DR | FAR | F1-Score | |
|---|---|---|---|---|---|
| CVA | 0.7485 | 0.9833 | 0.7655 | 0.2510 | 0.7572 |
| IRMAD | 0.6796 | 0.9818 | 0.5902 | 0.1736 | 0.6887 |
| ISFA | 0.6811 | 0.9816 | 0.6007 | 0.1886 | 0.6903 |
| CVA_MajorVote | 0.8018 | 0.9885 | 0.7091 | 0.0619 | 0.8077 |
| IRMAD_MajorVote | 0.7392 | 0.9861 | 0.6007 | 0.0161 | 0.7460 |
| ISFA_MajorVote | 0.7392 | 0.9861 | 0.6007 | 0.0161 | 0.7460 |
| MajorVote_Fusion | 0.7392 | 0.9861 | 0.6007 | 0.0161 | 0.7460 |
| D–S_Fusion | 0.8064 | 0.9888 | 0.7091 | 0.0501 | 0.8120 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Liu, C.; Wu, C.; Guo, X. Urban Change Detection Based on Dempster–Shafer Theory for Multitemporal Very High-Resolution Imagery. Remote Sens. 2018, 10, 980. https://doi.org/10.3390/rs10070980
Luo H, Liu C, Wu C, Guo X. Urban Change Detection Based on Dempster–Shafer Theory for Multitemporal Very High-Resolution Imagery. Remote Sensing. 2018; 10(7):980. https://doi.org/10.3390/rs10070980
Chicago/Turabian StyleLuo, Hui, Chong Liu, Chen Wu, and Xian Guo. 2018. "Urban Change Detection Based on Dempster–Shafer Theory for Multitemporal Very High-Resolution Imagery" Remote Sensing 10, no. 7: 980. https://doi.org/10.3390/rs10070980
APA StyleLuo, H., Liu, C., Wu, C., & Guo, X. (2018). Urban Change Detection Based on Dempster–Shafer Theory for Multitemporal Very High-Resolution Imagery. Remote Sensing, 10(7), 980. https://doi.org/10.3390/rs10070980