1. Introduction
Satellite remote sensing has become a vital tool in the arsenal of land managers, not only for the initial detection of active fire, but as part of inputs for modelling and planning purposes. Timely and accurate fire information from remote sensing enables preparation and planning for mitigation activities, along with providing vital information about fire behaviour and characteristics [
1]. Increasing importance is being placed upon active fire products to calculate metrics such as fire radiative power and burn severity [
2], in order to obtain an understanding of how the environment burns, and also to provide input for environmental modelling and quantifying outputs such as carbon emissions from fire.
Active fire detection from remote sensing relies on elevated levels of radiation in the infrared wavelengths caused by the blackbody radiation emitted from fire [
2]. The typical energy emitted by fire at medium-wave infrared (3–4
) wavelengths can be several orders of magnitude higher than regular radiation levels, which are primarily made up of thermal emission from the surface and solar reflection [
3,
4]. This disparity in energy levels allow fires that are much smaller than the pixel area to be detected, as the extra energy from a fire will overwhelm the background level of radiation [
1]. This propensity of fire to overwhelm the background signal presents a problem for fire detection purposes as well. The ability to determine whether a pixel is fire-affected is dependent upon knowing what the pixel should look like in the absence of fire [
5]. Accurate knowledge of the differential between fire signal and background allows fire to be detected, and enables the calculation of common fire-related metrics such as fire radiative power (FRP) [
6].
Without the ability to directly measure the background temperature of a pixel in the event of fire, fire algorithms have largely utilised the land area surrounding a target pixel to facilitate estimation of the background temperature, a method known as contextual estimation [
6,
7,
8,
9,
10,
11,
12]. For pixel brightness temperatures in the medium-wave infrared, spatial autocorrelation is primarily driven by latitude, with adjacent pixels receiving similar amounts of solar radiation, along with climatic conditions, which homogenise land cover over localised regions. This was highlighted in [
6], who stated that the assumption of neighbouring pixels having the same surface background characteristics was implicit in the fire algorithm developed in that work. This work [
6] also stated that “
…the extent to which this is true depends of surface spatial homogeneity and the sensor spatial resolution”. There has been no thorough examination of how surface homogeneity affects the accuracy of fire detection algorithms, despite this assumption being prevalent in active fire algorithms and products. Contextual measurements are also influenced by obscuration due to cloud or smoke, which may lead to decreased infrared radiation in pixels adjacent to a target pixel [
13]. Additionally, adjacency to water bodies may eliminate some pixels from being used in contextual calculations, with islands and coastal regions particularly susceptible to errors caused by reduced land surface availability. Examples of how these scenarios may influence the calculation of background temperature may be seen in
Figure 1.
Land surface temperature is a well covered topic in remote sensing [
14,
15,
16,
17,
18,
19], but most techniques focus upon use of thermal infrared (8–12
), which lacks a solar reflection component. This has led to an integration of land surface temperature techniques encompassing a combination of medium-wave and thermal infrared bands for fire detection purposes [
6,
9,
20,
21,
22], due to the differential response between these two wavelengths to emitted energy from fire. Such methods rely on accurate knowledge of the sensor response to temperature in both infrared bands and their relation to one another, and often rely on arbitrary statistical thresholds to relate the two bands for detection purposes, and studies such as [
23] have highlighted issues with the use of bispectral methods of fire detection. Algorithms exclusively using medium-wave infrared for background temperature detection have generally used this approach for calculation of metrics such as FRP, which is less reliant on highly accurate temperature information to achieve satisfactory results [
24,
25,
26].
The successful launch of the AHI-8 sensor in 2015 has expanded the availability of geostationary satellite image data for the Asia-Pacific, both in the spatial and temporal resolution domains [
27]. The increased spatial resolution of the sensor, which achieves 2 km × 2 km resolution in the medium-wave and thermal infrared bands, and the increased temporal coverage of the sensor, which records an as-yet unparalleled 10
refresh rate for geostationary full disk images, provide opportunities to image and analyse the sensor’s coverage area in far greater detail than previously [
28]. The fire detection and examination capabilities of the sensor have already been demonstrated in multiple studies [
12,
29,
30,
31]. These studies use a mix of contextual and multi-temporal techniques to detect and monitor fire activity, but as yet there has been no definitive fire algorithm for all conditions adopted for use with this sensor.
Fire detection algorithms perform a number of tests to not only isolate elevated sources of radiation, but to also eliminate false positive detections. Tests are usually made to mask cloud, which can trigger some detections through elevated reflectivity in the medium-wave infrared, for masking excess solar reflectivity in the form of sun glint, and to flag areas of water, which will bias infrared measurements downwards. Once these sources of error are eliminated from evaluation, decisions are then made about the suitability of pixels surrounding a potential fire for fire background temperature calculation. For instance, the MODIS MxD14 product [
20] uses values initially from a 3 × 3 (3 km) pixel window surrounding the target pixel (without the leading and trailing pixels in the cross-swath direction due to pixel smearing) to determine this temperature. The algorithm then tests how many suitable contextual pixels are available for evaluation, with a successful set of target pixels isolated for temperature calculation when the number of valid contextual pixels reaches at least 25% of the total, with a minimum of eight contextual pixels used for calculation. If the algorithm cannot find sufficient pixels at the first window (in this case, only six pixels are available and eight are required), the window expands to 5 × 5 pixels, and the tests are repeated. If the test fails again, the cycle repeats expanding the window to the maximum size of 21 × 21, at which point the tests conclude with no result.
This technique of the expanding window is not exclusively used for MODIS. The VIIRS VNP14 product [
32] has a background temperature calculation based upon a starting window of 11 × 11 (∼4 km in length), a success rate based on 25% of valid contextual pixels available for calculation and a 10 pixel minimum, and a maximum window range of 31 × 31 (∼10 km in length). The Fire Identification, Mapping and Monitoring Algorithm (FIMMA) for use on AVHRR sensors [
33] started with a 5 × 5 window, ended at the 41 × 41 pixel level, and used 35% of total contextual pixels available with a minimum number of eight pixels used. Work involving fire detection using Landsat-8 [
34] involved evaluation of a fixed 61 × 61 pixel window for background temperature calculation, with no limits placed upon the number of pixels used. Geostationary satellite algorithms apply these contextual tests as well–the MSG-SEVIRI sensor fire algorithm [
6] starts at a 5 × 5 window (15 km due to the sensor spatial resolution), with a maximum window size of 15 × 15 (45 km) evaluated before calculation failure. The pixels inside each window are tested against cloud, sun glint and anomalous differences between medium-wave and thermal infrared, and only if at least 65% valid context pixels are available will an estimation take place. This work on SEVIRI has also been extended for use on the GOES sensors [
17], with similar parameters used for contextual pixel utilisation.
These expanding window methods for evaluating temperature from the pixel context are applied to sensors with different spatial and radiometric characteristics, so they should differ slightly in application based upon each sensor. Despite this, apart from a rough relationship of spatial scaling between some of the products, there is no general consensus as to the ideal dimensions for contextual window evaluation, and indeed no optimal value for the minimum percentage of valid contextual pixels to use for deriving an accurate background temperature.
The objectives of this work are to examine common methods of deriving land surface temperature from a target’s surroundings in the context of fire detection. To achieve this, the enhanced temporal and spatial capabilities of the AHI-8 sensor are exploited in a large-area study. This paper presents the effects of variation of examined window sizes and valid contextual pixel percentages on background temperature. This work also highlights the challenges faced in using contextual estimation effectively, with in-depth examinations of a number of case study areas to determine the effectiveness of contextual temperature calculation.
2. Method
2.1. Data
This study utilises images from the Advanced Himawari Imager-8 (AHI-8), a geostationary sensor located at 140.7°E longitude [
35], data from which was obtained from the Japan Meteorological Agency (JMA) via the Australian Bureau of Meteorology (ABOM). This geostationary sensor provides coverage over the Asia-Pacific region over 16 bands, with an image captured every 10
. Images were obtained from the
medium-wave infrared band (AHI-8 Band 7) data, which is available in Australia from the National Computing Infrastructure (NCI). Dates were randomly selected for 36 days of the year 2016, with a distribution of three per calendar month in order to provide a representative sample of times in the results. The Julian dates selected were days 6, 10, 20, 35, 36, 41, 71, 72, 82, 97, 101, 103, 133, 144, 149, 153, 164, 173, 184, 188, 200, 222, 230, 236, 253, 257, 274, 279, 286, 290, 314, 322, 323, 343, 353 and 355 of 2016. A single image was examined at each of these days for the full disk examination, which was taken at 0500 UTC. This time was selected for full disk processing to maximise the amount of the land surface in daylight, along with examination of much of the disk at, or near, peak daily temperatures. This timing also coincides with the afternoon overpass of the VIIRS sensor for much of the land areas of the disk. This study utilises a cloud mask algorithm used in a study of AHI fire detection by [
30], which was adapted from use on the GOES–11 and GOES–12 geostationary sensors from [
24]. This mask is calculated using AHI Bands 3, 7 and 13, along with solar zenith information at each image time, from products supplied by ABOM.
To enable efficient processing of full disk images, the size of those captured by AHI, each full disk image was divided into component arrays of 500 × 500 pixels in size. The number of land pixels in each of these component arrays was then counted, and arrays containing less than 100 land pixels were discarded from analysis. Along with these omitted areas, arrays comprising solely land constituting the continent of Antarctica were also discarded. Once these tiles were identified, selections from each image with a 12 pixel buffer (for expanding window analysis purposes) were made of each tile and processing was performed. The areas with sufficient land for analysis are shown in
Figure 2.
As the focus of this study is determination of brightness temperature of land pixels, a land/sea mask supplied as part of the AHI ancillary data was applied to imagery to mask non-land pixels. Pixels close to the edge of the full disk are stretched over a large area of land surface, and also suffer from refraction due to the longer transmission period through the atmosphere. Pixels that have a sensor zenith angle greater than 80° were masked from further analysis using the AHI sensor ancillary product provided by ABOM.
2.2. AHI Disk Characterisation
Cloud is a major source of occlusion when measuring brightness temperature values. In order to obtain an understanding of the role cloud cover plays in an AHI full disk image, and by extension the distribution of clear sky pixels for analysis, the AHI image was broken into sub-images of 500 rows, for the first 5000 rows of the 5500 × 5500 image. The number of land pixels available in each of these sub-images was tallied, and the cloud coverage from the cloud mask was recorded for each full disk image. This breakdown of the AHI full disk into sub-images can be seen in the horizontal banding depicted in
Figure 2b.
The land area covered by AHI can be quite discontinuous, especially in the equatorial regions where many islands are present. These islands and coastal areas will have permanent gaps in their contextual coverage area due to the land forms surrounding them. In order to gain an understanding of the magnitude of these standing anomalies, an analysis of the land mask was conducted. Pixels were selected by the number of contextual pixels available for estimation during a cloud-free period, and categorised into percentage classes (75%, 65%, 55%, 45%, 35%, 25%, 15%). Pixels that had less than the required percentage of pixels available on the land mask were flagged, and counts of these unusable pixels were tabled.
To investigate the effectiveness of contextual estimation at a full disk level, the mean of all available contextual pixels was taken for each window size for each cloud-free pixel in the 36 images selected for study. The difference between each of these contextual estimates and the benchmark central pixel was calculated, and mean and standard deviations of these differences were aggregated for analysis. These values were further broken down by the exact percentage of contextual pixels available at each window level, in order to understand how the percentage of valid pixels affects the ultimate calculation of contextual temperature.
The size of the land area covered by individual pixels in a geostationary image increases as the sensor zenith angle increases. To determine whether this expansion of pixel area has an effect on contextual temperature calculations, all pixels from the dataset with contextual estimates were then divided into classes based upon their sensor zenith angle (eight classes spanning 10° from 0 to 80°), and statistics were aggregated for each of these classes.
2.3. Expanding the Window
As noted in the introduction, there have been many approaches taken to determine a suitable window size for contextual calculation, and no general consensus has been reached for ideal parameters, apart from a rough 10 km × 10 km maximum window size for the LEO sensor algorithms. For a geostationary sensor like AHI, we are limited as to the spatial bounds of the minimum window size we can select, as the sensor resolution prevents us from resolving at better than two kilometres in the infrared bands. A minimum sampling window of has been set around each pixel, which corresponds to 10 km × 10 km at sensor nadir. A number of window sizes were examined, with values selected in two pixel increments up to a maximum window size of 25 × 25 pixels. Each of these windows had a count of valid pixels, and the mean and standard deviation of differences between the contextual mean and the central pixel value recorded for each pixel for each image.
A common feature of contextual algorithms is the use of a threshold of valid pixels as a portion of the total examination window as a limiting factor for estimation validity. If the target pixel has at least the number of valid context pixels set by this threshold, the target’s contextual pixel values are used to calculate a temperature estimate, otherwise the target is ignored. There is no consensus upon which to base a definitive decision about valid context percentage choice—the most commonly used success criterion is 25% or an arbitrary number of pixels, as used by both MODIS and VIIRS in their respective fire products. This study has chosen to examine the use of seven percentage thresholds of contextual pixel availability, ranging from 75% to 15% in 10% increments. A pixel is deemed to have sufficient contextual data to make a calculation when the number of valid contextual pixels is equal to or greater than the selected percentage over the window being examined. For example, at the 5 × 5 window size, nine or more valid pixels need to be available for a temperature to be calculated at the 35% threshold. At some thresholds, land pixels with proximity to oceans and lakes may have insufficient land available to calculate a temperature.
Another commonly utilised feature of contextual algorithms is the expanding window. When insufficient data is available at an inner window size, the window of examination grows outwards until it obtains sufficient data to make a temperature determination. For a true evaluation of the effects of the expanding window on contextual estimation, it is important to know not only how often this window expansion occurs, but the effect the expanding window has upon calculated contextual estimations. For the expanding window section of this study, the portion of data with full contextual coverage at the window was analysed separately from pixels with at least one contextual pixel obscured. From the remaining pixels for each of the valid context percentages, pixels with sufficient context available at the were identified, and statistics calculated over these pixels. For the remaining pixels with no solution at the window at each valid context percentage, the window of examination was expanded to . At this point, the counts of valid context pixels were totalled for the current window and all previous windows. If the new number of contextual pixels was sufficient for the valid context percentage to be met, a contextual estimate was calculated over all contextual pixels available, and these statistics were recorded for reporting at the specified window size. After this, the examination window was expanded, and the process was repeated. Once the window of examination reached , some pixels were unable to find a solution based upon the selected percentage of valid contextual pixels. Counts of these failed pixels were also recorded.
Also, some expanding window methods will in addition use an absolute threshold for the number of valid contextual pixels required for temperature estimation. Once the number of contextual pixels available satisfies this threshold of valid pixels, a contextual estimate will be made based upon the available pixels regardless of the valid context percentage set. The work presented in this paper also examined the effects of using an absolute threshold of valid pixels of 10, similar to the VIIRS VNP14 product. For this, the window was firstly analysed, and as 10 pixels was the cutoff for validity for the 45% valid pixel class at , no higher valid contextual pixel percentages were examined. If a target pixel had either the required percentage of contextual pixels available, or sufficient contextual pixels to reach the absolute cutoff, the target pixel had a context temperature estimate calculated and recorded. Where this requirement was not met, the window was expanded to the next window size. If a target pixel did not reach either the valid contextual percentage or the absolute threshold of contextual pixels by the window, the target pixel was recorded as a failure and tallied.
2.4. Case Study Evaluation
A series of case study areas have also been evaluated in a more in-depth fashion, due to their land surface variation or their fire-prone nature. These areas include part of south-eastern Australia, part of north-western Australia, a section of Kalimantan’s east coast, part of central Thailand, part of eastern China, the central part of Honshu in Japan, and part of Siberia east of Lake Baikal. Each of these areas consists of a section of the AHI image measuring 200 × 200 pixels in size, with a small buffer to provide data for pixels at the edge of the selected window. These study areas are highlighted in
Figure 3.
In order to provide a more representative understanding of how each of these landscapes behaves during fire-prone periods, a selection of images for each case study area was made based upon the prevalence of fire over 2016. The monthly VIIRS fire product (VNP14IMGML) [
36] was subsampled for each of the study areas, and a rolling window of 30 days was applied to the sum total of fires from each area over the course of the year. The point of time exhibiting maximum fire activity from this was then used as the central day in a 31-day window for in-depth analysis. The image time selected for each case study area was also derived from the time of fires detected during the day time period in each case study area. The selection criteria for each case study area are detailed in
Table 1.
The counts of valid context pixels, and the difference of the context pixel mean from the central pixel were obtained for each window size, for each image, for each of the case study areas used for analysis. A visual examination of the causes of contextual estimate variation was also conducted based upon the spatial distribution of the mean temperature differences calculated, over window sizes from pixels to pixels, for each site.
4. Discussion
Whilst the numbers presented in
Section 3.1 are specific to the AHI disk coverage area, the same factors that restrict calculation of background temperature should be common to any part of the globe where fire detection and attribution occurs. Cloud coverage is a major inhibiting factor in any satellite fire detection setup, and areas that display even moderate occlusion of the contextual surroundings tend to present less than ideal estimations of temperature. From the range of values of contextual availability shown in
Figure 4a, there seems to be a break between results derived from pixels with at least 65% contextual availability and results from pixels with less contextual values available. The usage of estimates from target pixels with at least 65% available contextual information minimises the bias in the mean calculation of background temperature, especially at the larger window sizes, whilst also limiting the variation of the resultant estimations. The results presented in both
Table 4 and
Figure 4 also demonstrate the relative stability of temperatures derived from window sizes larger than
, or in AHI scale once pixels are at least 12 km from the pixel being estimated. If an increase in variance of calculated estimates of 60% over values derived at the
is acceptable for a specific purpose, then there is seemingly no reason not to set the initial area of examination for contextual temperature as large as practicable, but if this temperature variance is more of a concern, then using pixels from outside even the
window of pixels becomes problematic.
The effects at play when calculating contextual estimates as shown in
Figure 4 bear further examination. The relative differences between the mean and variation seen at the higher window sizes reduces as the pixels examined increase in distance from the target, an effect noted in
Section 3.1 being due to variations in the window edge radius. Examination of the effect of using pixels with similar distances to the target, in a circular ring, would most likely bear this out, though implementation of such a distance-based window of examination would become less trivial as sensor zenith angle increases. The pattern of mean difference as a function of valid pixels is worth mentioning as well, especially with regard to overestimation of the target temperature when valid contextual pixels approach 50%. This effect is likely due to shadowing of the target pixel and consequent reduction in solar reflectivity, with the target pixel most likely being immediately adjacent to the obscuration affecting the surrounding pixels. This effect is lessened in the rings of pixels situated further from the target pixel, as the source of obscuration at the outer edge of the window is less likely to be present closer in to the target pixel. This overestimation is not particularly large in magnitude, and is less likely to affect fire detection for instance, but such information may assist in the adjustment of temperature-controlled metrics calculated from these estimates.
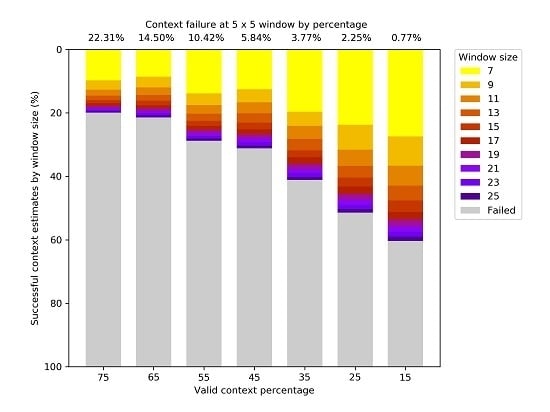
The results also cast the use of expanding windows for contextual temperature examination in a poor light, particularly for those sensors with larger spatial resolutions. The vast majority of all pixel calculations are achieved at the window, with the recovery of data from using an expanding window ranging from 20% to 54% of all remaining target pixels. If we are to use the 65% window as an example, 85% of data is contributed from the window, extra estimates from using the expanding window are just over 4%, and the majority of those extra estimates occur at or below the window. There are also compromises involved in using the estimates, with a general positive bias and much higher variation in values at even the level. Depending on the purpose of using these estimates, using the data coming from the combined windows could be detrimental to the overall reporting accuracy. When evaluating how a background temperature method should be implemented, care needs to be taken to ensure that any need for comprehensive coverage, whether it be achieved by either using a smaller percentage of valid contextual pixels, by using larger window sizes, or both, does not inhibit the accuracy of the overall product.
With regard to the case study areas selected for analysis, the reasons for major variances in contextually determined temperature are as diverse as the case study sites selected. Phenomena affecting contextual estimation range from highly ephemeral conditions, such as fire and flooding, to seasonally changing influences such as snow and vegetation cover, to semi-permanent influences such as urban–rural interfaces and land cover change, and on to permanent conditions such as relief, tree lines and coastlines. Each of these influencing factors needs to be treated in a different way dependent upon the expected temporal duration of phenomena. Whilst setting global thresholds is satisfactory for more holistic measures such as carbon emissions and global FRP [
10], in order to obtain more accurate estimates of pixel contrast, for metrics which require more accurate estimates of pixel temperature, the use of a contextual method may require the application of a-priori information. Conversely, a method that takes local variation into account by using such information needs to take into account the changes caused by more short-term influences mentioned here. This adds complexity to any system that uses fire background temperature in a rapid fashion, such as in active fire response.
Whilst this study demonstrates the effectiveness of contextual estimation when conditions are amenable, the deterioration of temperature estimation fidelity, and in some cases total loss of recovery, leads to the investigation of other methods that may be able to bridge the gap in temperature retrieval. Investigation should be encouraged into the leveraging information from the temporal domain when looking at this problem. Methods such as those used in [
25,
31,
37] look at the diurnal temporal domain for temperature estimation, which is more suited to geostationary sensors such as AHI and GOES. This does not preclude the use of temporal information for LEO products though. An approach to the integration of temporal modelling of background temperature could look at the adjustment of measurements by images from previous time periods, with adjustments made for factors such as time of image capture. Looking at many different time points would provide redundancy against ephemeral conditions such as cloud, but looking too far back in time can lead to information not being representative of the current state of the landscape. A mix of ephemeral, seasonal and annual adjustments should be examined for their effectiveness in correcting estimated values for LEO-based products.
With regard to the direct applicability of these results to products and values from other sensors, caution should be exercised. The pixel sizes examined here from the AHI-8 sensor are much larger than their equivalents from images taken by low earth orbiting sensors. The rapid changes in landforms and land cover types seen in the case study areas may be smoothed or exacerbated by using smaller pixels, and the overall granularity of spatial homogeneity at varying scales should be taken into account when making comparisons across products and sensor scales. Sensor-dependent effects such as sensor point spread function have also not been examined here, although these effects are mostly seen when dealing with high temperature anomalies in the MWIR band, which the vast majority of target pixels in this study do not encounter. The orbit of the sensor used in this study also grants the opportunity to examine targets at the same local time over many images, and the application of methods used for analysis of LEO sensor information in a similar fashion would need to take into account variations in the time of image capture for longitudinal analysis purposes.
This study has assessed the overall ability to estimate background temperature from spatial context using AHI. In this study, temperature estimates from pixels with all context pixels available show a standard deviation of when examined across the full disk. In comparison, the global standard deviations for the case study areas were higher, ranging from in Siberia to in Japan. Whilst the accuracy of background temperature is less emphasised for metrics such as FRP, information obtained from this study could be used in an adjustment of these metrics as calculated from AHI. Knowledge about the expected variation of medium-wave infrared radiation estimation may also play a role in the development of new fire detection techniques, which use the expected variation of MWIR radiation in an area to identify anomalous values as a first-pass filter. Providing simpler and more concise algorithms for fire detection reduces the data volumes and processing overhead required, leading to the more rapid production and application of results.