Determination of Soil Salt Content Using a Probability Neural Network Model Based on Particle Swarm Optimization in Areas Affected and Non-Affected by Human Activities
Abstract
:1. Introduction
2. Data Collection
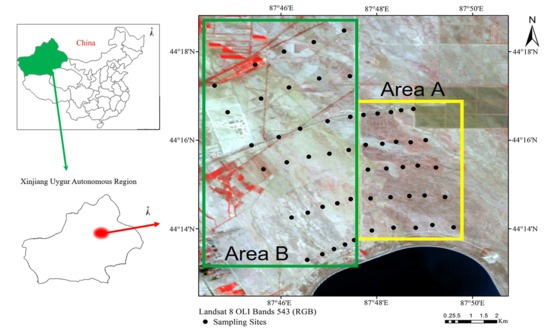
2.1. Overview of the Study Area
2.2. Soil Sample Collection
2.3. Obtaining Spectrum Data
3. Methodology
3.1. Probability Neural Network
3.2. Particle Swarm Optimization
3.3. Model Verification
4. Spectrum Data Pre-Processing
4.1. Removing Interfering Wave Bands
4.2. Savitzky-Golay Convolution Smoothing
4.3. Multiple-Spectrum Mathematical Transformation
5. Simulation Results
5.1. Five Wave Band Intervals
5.2. Optimal Smoothing Parameter
5.3. Evaluation Indicators for Area A
5.4. Area A Prediction Results
5.5. Area B Evaluation Indicators
5.6. Area B Prediction Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nawar, S.; Buddenbaum, H.; Hill, J. Digital mapping of soil properties using multivariate statistical analysis and ASTER data in an arid region. Remote Sens. 2015, 7, 1181–1205. [Google Scholar] [CrossRef]
- Ding, J.L.; Yu, D.L. Monitoring and evaluating spatial variability of soil salinity in dry and wet seasons in the Werigan-Kuqa Oasis, China, using remote sensing and electromagnetic induction instruments. Geoderma 2014, 235, 316–322. [Google Scholar] [CrossRef]
- Marcos, R.G.; Fauze, A.A.; André, R.F.; Alessandro, F.M.; Alexandre, T.P.; Magali, F.T.D.; Adley, F.R.; Edvani, C.M. Superabsorbent hydrogels based on polysaccharides for application in agriculture as soil conditioner and nutrient carrier: A review. Eur. Polym. J. 2015, 72, 365–385. [Google Scholar]
- Hu, G.T.; He, D.; Kenneth, A.S. Soil phosphorus and potassium estimation using visible-near infrared reflectance spectroscopy with direct orthogonal signal correction. Trans. Chin. Soc. Agric. Mach. 2015, 46, 139–145. [Google Scholar]
- Li, J.G.; Pu, L.J.; Han, M.F.; Zhu, M.; Zhang, R.S.; Xiang, Y.Z. Soil salinization research in China: Advances and prospects. J. Geogr. Sci. 2014, 24, 943–960. [Google Scholar] [CrossRef]
- McLeod, M.K.; Slavich, P.G.; Irhas, Y.; Moore, N.; Rachman, A.; Ali, N.; Iskandar, T.; Hunt, C.; Caniago, C. Soil salinity in Aceh after the December 2004 Indian Ocean tsunami. Agric. Water Manag. 2010, 97, 605–613. [Google Scholar] [CrossRef]
- Metternicht, G.I.; Zinck, J.A. Remote sensing of soil salinity: Potentials and constraints. Remote Sens. Environ. 2003, 85, 1–20. [Google Scholar] [CrossRef]
- Allbed, A.; Kumar, L.; Sinha, P. Mapping and modeling spatial variation in soil salinity in the Al Hassa Oasis based on remote sensing indicators and regression techniques. Remote Sens. 2014, 6, 1137–1157. [Google Scholar] [CrossRef]
- Farifteh, J.; Farshad, A.; George, R.J. Assessing salt-affected soils using remote sensing, solute modeling, and geophysics. Geoderma 2006, 130, 191–206. [Google Scholar] [CrossRef]
- Liu, S.L.; Maimaitiaili, B.; Joergensen, R.G.; Feng, G. Response of soil microorganisms after converting a saline desert to arable land in central Asia. Appl. Soil Ecol. 2016, 98, 1–7. [Google Scholar] [CrossRef]
- Dinh, H.Q.; Fotedar, R. Early development of the blue mussel Mytilus edulis (Linnaeus, 1758) cultured in potassium-fortified inland saline water. Aquaculture 2016, 452, 373–379. [Google Scholar] [CrossRef]
- Fan, X.; Pedroli, B.; Liu, G.; Liu, Q.; Liu, H.; Shu, L. Soil salinity development in the yellow river delta in relation to groundwater dynamics. Land Degrad. Dev. 2011, 23, 175–189. [Google Scholar] [CrossRef]
- Weng, Y.; Gong, P.; Zhu, Z. Soil salt content estimation in the Yellow River delta with satellite hyperspectral data. Can. J. Remote Sens. 2008, 34, 259–270. [Google Scholar]
- Herrero, J.; Netthisinghe, A.; Hudnall, W.H.; Pérez, C.O. Electromagnetic induction as a basis for soil salinity monitoring within a Mediterranean irrigation district. J. Hydrol. 2011, 405, 427–438. [Google Scholar] [CrossRef] [Green Version]
- Ding, J.L.; Wu, M.C.; Tashpolat, T. Study on soil salinization information in Arid Region using remote sensing technique. Agric. Sci. Chin. 2011, 10, 404–411. [Google Scholar] [CrossRef]
- Brunner, P.; Li, H.T.; Kinzelbach, W. Generating soil electrical conductivity maps at regional level by integrating measurements on the ground and remote sensing data. Int. J. Remote Sens. 2007, 28, 3341–3361. [Google Scholar] [CrossRef]
- Sahu, N.; Singh, S.K.; Reddy, G.P.O.; Kumar, N.; Nagaraju, M.S.S.; Srivastava, R. Large-Scale Soil Resource Mapping Using IRS-P6 LISS-IV and Cartosat-1 DEM in Basaltic Terrain of Central India. J. Indian Soc. Remote Sens. 2016, 44, 811–819. [Google Scholar] [CrossRef]
- Joshi, N.; Baumann, M.; Ehammer, A.; Fensholt, R.; Grogan, K.; Hostert, P.; Jepsen, M.; Kuemmerle, T.; Meyfroidt, P.; Mitchard, E.; et al. A review of the application of optical and radar remote sensing data fusion to land use mapping and monitoring. Remote Sens. 2016, 8, 1–23. [Google Scholar] [CrossRef]
- Wu, W.C.; Mhaimeed, A.S.; Al-Shafie, W.M.; Ziadat, F.; Dhehibi, B.; Nangia, V.; Pauw, E.D. Mapping soil salinity changes using remote sensing in Central Iraq. Geoderma Regional. 2014, 23, 21–31. [Google Scholar] [CrossRef]
- Lobell, D.B.; Ortizmonasterio, J.I.; Gurrola, F.C.; Valenzuela, L. Identification of saline soils with multiyear remote sensing of crop yields. Soil Sci. Soc. Am. 2007, 71, 777–783. [Google Scholar] [CrossRef]
- Cao, L.; Ding, J.L.; Yu, H.Y. Relationship between multi-scale landscape pattern and salinity in Weigan and Kuqa rivers delta oasis. Trans. Chin. Soc. Agric. Eng. 2016, 32, 101–110. [Google Scholar]
- Luan, F.M.; Zhang, X.L.; Xiong, H.; Zhang, F.; Wang, F. Comparative Analysis of Soil Organic Matter Content Based on Different Hyperspectral Inversion Models. Spectrosc. Spectr. Anal. 2013, 33, 196–200. [Google Scholar]
- Han, Y.; Xu, W.R.; Jin, L. Study on the polarized reflectance hyperspectral characteristics and models of typical saline soil. J. Infrared Millim. Waves 2015, 34, 606–612. [Google Scholar]
- Ding, J.L.; Wu, M.C.; Liu, H.X.; Li, Z.G. Study on the soil salinization monitoring based on synthetical hyperspectral index. Spectrosc. Spectr. Anal. 2012, 32, 1918–1922. [Google Scholar]
- Viscarra, R.R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Debaene, G.; Niedźwiecki, J.; Pecio, A.; Żurek, A. Effect of the number of calibration samples on the prediction of several soil properties at the farm-scale. Geoderma 2014, 214, 114–125. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Patkin, K.; Banin, A.; Karnieli, A. Mapping of several soil properties using DAIS-7915 hyperspectral scanner data. A case study over clayey soils in Israel. Int. J. Remote Sens. 2002, 23, 1043–1062. [Google Scholar] [CrossRef]
- Qu, Y.H.; Duan, X.L.; Gao, H.Y.; Chen, A.P.; An, Y.Q.; Song, J.L.; Zhou, H.M.; He, T. Quantitative retrieval of soil salinity using hyperspectral data in the region of Inner Mongolia Hetao irrigation district. Spectrosc. Spectr. Anal. 2009, 29, 1362–1366. [Google Scholar]
- Liu, X.Y.; Shi, Z.Y.; Chang, Q.R.; Liu, C.Z.; Huang, M.; Gu, X. Hyperspectral Model for Estimation of Soil Potassium Content in Loessal soil. Acta Pedologica Sin. 2018, 55, 325–337. [Google Scholar]
- Liu, X.M.; Liu, J.S. Based on the LS-SVM modeling method determination of soil available N and available K by using near-infrared spectroscopy. Spectros. Spectr. Anal. 2012, 32, 3019–3023. [Google Scholar]
- Farifteh, J.; Meer, F.V.D.; Atzberger, C.; Carranza, E.J.M. Quantitative analysis of salt-affected soil reflectance spectra: A comparison of two adaptive methods (PLSR and ANN). Remote Sens. Environ. 2017, 110, 59–78. [Google Scholar] [CrossRef]
- Weng, Y.L.; Gong, P.; Zhu, Z.L. A Spectral Index for Estimating Soil Salinity in the Yellow River Delta Region of China Using EO-1 Hyperion Data. Pedosphere 2010, 20, 378–388. [Google Scholar] [CrossRef]
- Sidike, A.; Zhao, S.H.; Wen, Y.M. Estimating soil salinity in Pingluo County of China using QuickBird data and soil reflectance spectra. Int. J. App. Earth Obs. Geoinf. 2014, 26, 156–175. [Google Scholar] [CrossRef]
- Zhang, X.G.; Huang, B.; Ji, J.F.; Hu, W.Y.; Sun, W.X.; Zhao, Y.C. Quantitative prediction of soil salinity content with visible-near infrared hyper-spectra in Northeast China. Spectrosc. Spectr. Anal. 2012, 32, 2075–2079. [Google Scholar]
- Specht, D.F. Probabilistic neural networks. Neural Netw. 1990, 3, 109–118. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Yau, H.T.; Hung, T.H.; Hsieh, C.C. Bluetooth based chaos synchronization using particle swarm optimization and its applications to image encryption. Sensors 2012, 12, 7468–7484. [Google Scholar] [CrossRef] [PubMed]
- Selvakumar, A.I.; Thanushkodi, K. A new particle swarm optimization solution to nonconvex economic dispatch problems. IEEE Trans. Power Syst. 2007, 22, 42–51. [Google Scholar] [CrossRef]
- Qiao, X.X.; Wang, C.; Feng, M.; Yang, W.D.; Ding, G.W.; Sun, H.; Liang, Z.Y.; Shi, C.C. Hyperspectral estimation of soil organic matter based on different spectral preprocessing techniques. Spectrosc. Lett. 2017, 50, 156–163. [Google Scholar] [CrossRef]
- Rocha, O.C.D.; Teixeira, A.; Leão, R.; Moreira, L.C.J.; Galvão, L.S. Hyperspectral remote sensing for detecting soil salinization using ProSpecTIR-VS aerial imagery and sensor simulation. Remote Sens. 2017, 9, 1–16. [Google Scholar] [CrossRef]
- Liu, H.J.; Zhang, X.L.; Zheng, S.F.; Tang, N.; Hu, Y.L. Black soil organic matter predicting model based on field hyperspectral reflectance. Spectrosc. Spectr. Anal. 2010, 30, 3355–3358. [Google Scholar]
- Zheng, X.P.; Sun, Y.J.; Qin, Q.M.; Ren, H.Z.; Gao, Z.L.; Wu, L.; Meng, Q.Y.; Wang, J.L.; Wang, J.H. Bare soil moisture inversion model based on visible-shortwave infrared reflectance. Spectrosc. Spectr. Anal. 2015, 35, 2113–2118. [Google Scholar]
- Liu, X.Y.; Wang, L.; Chang, Q.R.; Song, R.J. Prediction of moisture content in loess using continuum-removed method. Geomat. Inf. Sci. Wuhan Univ. 2017, 42, 661–668. [Google Scholar]
- Stoner, E.R.; Baumgardner, M.F. Characteristic variation in reflectance of surface of surface soils. Soil Sci. Soc. Am. J. 1981, 45, 1161–1165. [Google Scholar] [CrossRef]
- Bowers, S.A.; Hanks, R.J. Reflection of radiant energy from soils. Soil Sci. 1965, 100, 130–138. [Google Scholar] [CrossRef]
- Zhao, Z.L.; Tashpolat, T.; Sun, Q.; Lei, L.; Zhang, F. Soil spectrum characteristics and information extraction of salinization: A case study in Weigan-Kuqa Oasis in Xinjiang. Prog. Geogr. 2014, 33, 280–288. [Google Scholar]
- Dehaan, R.L.; Taylor, G.R. Field-derived spectra of salinized soils and vegetation as indicators of irrigation-induced soil salinization. Remote Sens. Environ. 2002, 80, 406–417. [Google Scholar] [CrossRef]
- Li, J.; Wang, K.R.; Li, S.K.; Chen, B.; Xiao, C.H.; Wang, Q.; Wang, F.Y.; Li, S.M.; Lai, J.C.; Sun, Y.L.; et al. Cotton Soil Salinity Monitoring Based on a Spectrum-Salt Index. Cotton Sci. 2014, 26, 555–562. [Google Scholar]
- Wang, J.; Liu, X.N.; Huang, F.; Tang, J.L.; Zhao, L.B. Salinity predicting of saline soil based on ANN and hyperspectral remote sensing. Trans. Chin. Soc. Agric. Eng. 2009, 25, 161–166. [Google Scholar]
- Zhu, Y.; Shen, G.G.; Wang, Z.J.; Lu, S.M.; Zhi, Y.E.; Xiang, Q.Q. Soil salt content and its spectral characteristics during microbial remediation processes. Spectrosc. Spectr. Anal. 2017, 37, 1507–1513. [Google Scholar]











| Wavelength | Signal | R | 1/R | log(1/R) | log(R) | 1/log(R) | |
|---|---|---|---|---|---|---|---|
| 400–700 nm | Original | 0.880219 | 0.846142 | 0.24551 | 0.432957 | 0.432957 | 0.623002 |
| SG | 0.88395 | 0.851433 | 0.227578 | 0.4545 | 0.4545 | 0.634666 | |
| 700–1000 nm | Original | 0.666516 | 0.715382 | 0.237389 | 0.413956 | 0.413956 | 0.4538 |
| SG | 0.669802 | 0.718228 | 0.293012 | 0.445924 | 0.445924 | 0.479089 | |
| 1000–1350 nm | Original | 0.503986 | 0.574182 | 0.18463 | 0.313566 | 0.313566 | 0.303839 |
| SG | 0.512374 | 0.5803 | 0.140863 | 0.303304 | 0.303304 | 0.290997 | |
| 1455–1805 nm | Original | 0.98773 | 1.092727 | 0.319539 | 0.598944 | 0.598944 | 0.587325 |
| SG | 0.997925 | 1.103375 | 0.350219 | 0.61947 | 0.61947 | 0.610725 | |
| 2000–2400 nm | Original | 0.600098 | 0.663767 | 0.211646 | 0.368735 | 0.368735 | 0.360034 |
| SG | 0.659119 | 0.711643 | 0.322248 | 0.466626 | 0.466626 | 0.460637 |
| Wavelength | Signal | R | 1/R | log(1/R) | log(R) | 1/log(R) | |
|---|---|---|---|---|---|---|---|
| 400–700 nm | Original | 0.980265 | 0.981634 | 0.998564 | 0.995391 | 0.995391 | 0.990327 |
| SG | 0.980088 | 0.981386 | 0.998599 | 0.994626 | 0.994626 | 0.989803 | |
| 700–1000 nm | Original | 0.993754 | 0.992662 | 0.994437 | 0.997762 | 0.997762 | 0.997385 |
| SG | 0.993514 | 0.992418 | 0.998454 | 0.997112 | 0.997112 | 0.996863 | |
| 1000–1350 nm | Original | 0.994176 | 0.992279 | 0.999183 | 0.997733 | 0.997733 | 0.99795 |
| SG | 0.993888 | 0.992063 | 0.999374 | 0.997755 | 0.997755 | 0.99801 | |
| 1455–1805 nm | Original | 0.97765 | 0.972195 | 0.998362 | 0.992584 | 0.992584 | 0.992823 |
| SG | 0.97698 | 0.971436 | 0.997082 | 0.991397 | 0.991397 | 0.991483 | |
| 2000–2400 nm | Original | 0.991189 | 0.989169 | 0.999038 | 0.996719 | 0.996719 | 0.996814 |
| SG | 0.988771 | 0.987007 | 0.997086 | 0.993908 | 0.993908 | 0.993993 |
| Wavelength | Signal | R | 1/R | log(1/R) | log(R) | 1/log(R) | |
|---|---|---|---|---|---|---|---|
| 400–700 nm | Original | 6.400056 | 6.657809 | 22.94595 | 13.01157 | 13.01157 | 9.042428 |
| SG | 6.373043 | 6.616435 | 24.75394 | 12.39483 | 12.39483 | 8.876255 | |
| 700–1000 nm | Original | 8.452091 | 7.874745 | 23.7309 | 13.60883 | 13.60883 | 12.41394 |
| SG | 8.410621 | 7.843541 | 19.22602 | 12.63322 | 12.63322 | 11.75867 | |
| 1000–1350 nm | Original | 11.17781 | 9.811266 | 30.51219 | 17.96574 | 17.96574 | 18.54091 |
| SG | 10.9948 | 9.707836 | 39.99251 | 18.57365 | 18.57365 | 19.35916 | |
| 1455–1805 nm | Original | 5.703437 | 5.155406 | 17.62992 | 9.405647 | 9.405647 | 9.591717 |
| SG | 5.645165 | 5.105654 | 16.0855 | 9.09399 | 9.09399 | 9.224208 | |
| 2000–2400 nm | Original | 9.38756 | 8.487099 | 26.61728 | 15.27779 | 15.27779 | 15.64701 |
| SG | 8.546946 | 7.916121 | 17.48176 | 12.07275 | 12.07275 | 12.2297 |
| Wavelength | Signal | R | 1/R | log(1/R) | log(R) | 1/log(R) | |
|---|---|---|---|---|---|---|---|
| 400–700 nm | Original | 1.652057 | 1.578996 | 0.362379 | 0.755131 | 0.755131 | 1.10885 |
| SG | 1.395946 | 1.33715 | 0.281027 | 0.658492 | 0.658492 | 0.984695 | |
| 700–1000 nm | Original | 1.881389 | 2.027826 | 0.670349 | 1.195093 | 1.195093 | 1.270434 |
| SG | 1.885963 | 2.034313 | 0.741881 | 1.177413 | 1.177413 | 1.253372 | |
| 1000–1350 nm | Original | 1.172402 | 1.277664 | 0.416209 | 0.684781 | 0.684781 | 0.676523 |
| SG | 1.171473 | 1.277971 | 0.506309 | 0.725767 | 0.725767 | 0.720614 | |
| 1455–1805 nm | Original | 0.940534 | 1.066988 | 0.331386 | 0.573277 | 0.573277 | 0.518566 |
| SG | 0.962209 | 1.087288 | 0.338851 | 0.623245 | 0.623245 | 0.579542 | |
| 2000–2400 nm | Original | 1.264737 | 1.395243 | 0.574168 | 0.894886 | 0.894886 | 0.823833 |
| SG | 1.083877 | 1.263583 | 0.358336 | 0.582145 | 0.582145 | 0.508204 |
| Wavelength | Signal | R | 1/R | log(1/R) | log(R) | 1/log(R) | |
|---|---|---|---|---|---|---|---|
| 400–700 nm | Original | 0.981787 | 0.98322 | 0.999088 | 0.996064 | 0.996064 | 0.992045 |
| SG | 0.989466 | 0.99 | 0.999208 | 0.998047 | 0.998047 | 0.995474 | |
| 700–1000 nm | Original | 0.967022 | 0.961644 | 0.995763 | 0.986701 | 0.986701 | 0.984855 |
| SG | 0.966294 | 0.960977 | 0.994643 | 0.986877 | 0.986877 | 0.985058 | |
| 1000–1350 nm | Original | 0.990661 | 0.989318 | 0.998602 | 0.996765 | 0.996765 | 0.996747 |
| SG | 0.990562 | 0.989185 | 0.998028 | 0.996127 | 0.996127 | 0.996085 | |
| 1455–1805 nm | Original | 0.995222 | 0.993748 | 0.999069 | 0.998343 | 0.998343 | 0.998549 |
| SG | 0.994733 | 0.993217 | 0.999017 | 0.997754 | 0.997754 | 0.997931 | |
| 2000–2400 nm | Original | 0.984271 | 0.981215 | 0.996815 | 0.992047 | 0.992047 | 0.99292 |
| SG | 0.990315 | 0.986701 | 0.996413 | 0.99785 | 0.99785 | 0.998264 |
| Wavelength | Signal | R | 1/R | log(1/R) | log(R) | 1/log(R) | |
|---|---|---|---|---|---|---|---|
| 400–700 nm | Original | 6.047578 | 6.327404 | 27.5704 | 13.23074 | 13.23074 | 9.010187 |
| SG | 7.157114 | 7.47182 | 35.55161 | 15.17245 | 15.17245 | 10.14623 | |
| 700–1000 nm | Original | 5.310409 | 4.926924 | 14.9041 | 8.359976 | 8.359976 | 7.864198 |
| SG | 5.29753 | 4.911213 | 13.46704 | 8.485507 | 8.485507 | 7.971253 | |
| 1000–1350 nm | Original | 8.521775 | 7.819697 | 24.00465 | 14.58998 | 14.58998 | 14.76808 |
| SG | 8.528532 | 7.817816 | 19.73291 | 13.76605 | 13.76605 | 19.26648 | |
| 1455–1805 nm | Original | 10.62263 | 9.363695 | 30.149 | 17.42778 | 17.42778 | 19.26648 |
| SG | 10.38334 | 9.188868 | 29.48481 | 16.03053 | 16.03053 | 17.23937 | |
| 2000–2400 nm | Original | 7.899625 | 7.160722 | 17.40074 | 11.16449 | 11.16449 | 12.12738 |
| SG | 9.217781 | 7.906835 | 27.88154 | 17.1623 | 17.1623 | 19.65932 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, C.; Gan, S.; Yuan, X.; Xiong, H.; Tian, A. Determination of Soil Salt Content Using a Probability Neural Network Model Based on Particle Swarm Optimization in Areas Affected and Non-Affected by Human Activities. Remote Sens. 2018, 10, 1387. https://doi.org/10.3390/rs10091387
Fu C, Gan S, Yuan X, Xiong H, Tian A. Determination of Soil Salt Content Using a Probability Neural Network Model Based on Particle Swarm Optimization in Areas Affected and Non-Affected by Human Activities. Remote Sensing. 2018; 10(9):1387. https://doi.org/10.3390/rs10091387
Chicago/Turabian StyleFu, Chengbiao, Shu Gan, Xiping Yuan, Heigang Xiong, and Anhong Tian. 2018. "Determination of Soil Salt Content Using a Probability Neural Network Model Based on Particle Swarm Optimization in Areas Affected and Non-Affected by Human Activities" Remote Sensing 10, no. 9: 1387. https://doi.org/10.3390/rs10091387
APA StyleFu, C., Gan, S., Yuan, X., Xiong, H., & Tian, A. (2018). Determination of Soil Salt Content Using a Probability Neural Network Model Based on Particle Swarm Optimization in Areas Affected and Non-Affected by Human Activities. Remote Sensing, 10(9), 1387. https://doi.org/10.3390/rs10091387