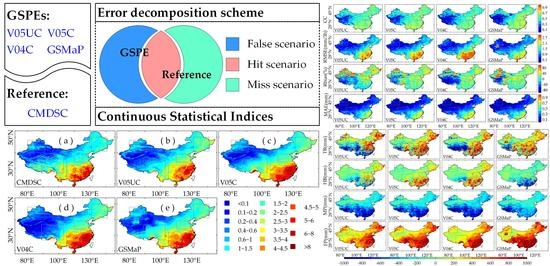
Component Analysis of Errors in Four GPM-Based Precipitation Estimations over Mainland China
Abstract
:1. Introduction
2. Study Site and Materials
2.1. Study Areas
2.2. Ground Reference Data
2.3. Satellite-Based Precipitation Products
2.3.1. IMERG Products
2.3.2. GSMaP Product
3. Methods
3.1. Continuous Statistical Indices
3.2. Error Decomposition
4. Results
4.1. Spatiotemporal Analyses of Precipitation Accumulation
4.2. Spatial Statistical Analysis
4.3. Error Components Analysis
4.4. Intensity Distribution Analysis
5. Discussion
6. Conclusions
- (1)
- Compared to the CMDSC, the four GSPEs could generally capture the spatial patterns of precipitation over mainland China in spite of the overestimation in the southeast and the underestimation in the northern Tibetan Plateau. Overall, the quality of the four GSPEs in the humid and flat east was better than that in the arid and hypsographic west, with higher CCs of approximately 0.6 occurring in the east, but relatively lower CCs appearing in the west.
- (2)
- In regional analysis, two calibrated IMERG products (V05C and V04C) showed similar performances in both detecting accurate daily average precipitation and capturing 3-h-scale regional averaged precipitation accumulation over regions 1–4. The uncalibrated V05UC achieved comparable performance to calibrated IMERG products over these regions. This indicated that the latest IMERG (V05UC and V05C) did not achieve superior improvement in these areas, despite the slight improvement in detecting regional heavy precipitation events. Moreover, GSMaP outperformed all of the IMERG products in regions 1–4 in regard to almost all of the metrics. However, all four products should improve their quality in arid areas (Region 5) and the Tibet Plateau (Region 6) for better application.
- (3)
- The error components and TB of the four GSPEs showed strong regional differences over mainland China. Much of the overestimations over the North China Plain and northeastern China for IMERG V05 can be traced to significant FP and noticeable HB. Since the GCA used in IMERG V05 was prone to increase the rain rates over the southern Tibetan Plateau and southeastern China, the negative HB had been changed to positive, and FP was significantly enlarged, but could not correct the MP. Thus, the negative TB contained in V05UC had been turned to positive over these regions. V04C had similar error component distributions to V05C except for over the Tibetan Plateau, where larger MP and non-negligible negative HB had generated remarkable TB. For GSMaP, much of the overestimations over the east and south are the comprehensive impact of HB and FP, although MP may counteract some of this impact.
- (4)
- The regional time-series analyses clearly illustrated that the TB resulted from the interaction of the three independent components. The positive HB and FP played a dominant role in the overestimation of IMERG over northeast China (regions 1–2). Benefiting from the mutual melting of FP and MP, the curves of HB in IMERG were very close to the corresponding TB over south China (regions 3–4), although a more obviously positive HB appeared in the calibrated IMERG. The uncertainty in IMERG caused by MP and FP cannot be ignored in high-altitude (Regions 6) and dry (Region 5) areas, particularly for V04C in the Tibetan Plateau, where it showed obvious underestimation principally caused by MP. Larger FP was a main problem of GSMaP over almost the entirety of China. Meanwhile, the HB contained in GSMaP over Region 4 also needs to be noted.
- (5)
- From the perspective of the intensity distribution, V05C can best match the PDF of CMDSC over almost all of the regions, but the overestimation in heavy rain, which was mainly caused by positive HB, was still a large problem. V05UC had better ability than V05C in detecting heavy rain. In addition, GSMaP tended to overrate light rain and underrate heavy rain, particularly for regions 1–4. Such overestimation and underestimation were mainly caused by large FP in light rain and negative HB in heavy rain, respectively.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hong, Y.; Adler, R.F.; Huffman, G.J.; Pierce, H. Applications of Trmm-Based Multi-Satellite Precipitation Estimation for Global Runoff Prediction: Prototyping a Global Flood Modeling System; Springer: Berlin, Germany, 2010; pp. 245–265. [Google Scholar]
- Su, J.; Lü, H.; Wang, J.; Sadeghi, A.M.; Zhu, Y. Evaluating the applicability of four latest satellite–gauge combined precipitation estimates for extreme precipitation and streamflow predictions over the upper yellow river basins in China. Remote Sens. 2017, 9, 1176. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Conti, F.L.; Hsu, K.L.; Noto, L.V.; Sorooshian, S. Evaluation and comparison of satellite precipitation estimates with reference to a local area in the mediterranean sea. Atmos. Res. 2014, 138, 189–204. [Google Scholar] [CrossRef]
- Dinku, T.; Anagnostou, E.N.; Borga, M. Improving radar-based estimation of rainfall over complex terrain. J. Appl. Meteorol. 2002, 41, 1163–1178. [Google Scholar] [CrossRef]
- Mei, Y.; Anagnostou, E.N.; Nikolopoulos, E.I.; Borga, M. Error analysis of satellite precipitation products in mountainous basins. J. Hydrometeorol. 2014, 15, 1778–1793. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Xue, X.; Hodges, G. Global precipitation estimation and applications. In Multiscale Hydrologic Remote Sensing: Perspectives and Applications; CRC Press: Boca Raton, FL, USA, 2012; pp. 371–386. [Google Scholar]
- Barrera, D.F.; Ceirano, E.; Zucarelli, G.V. Differences in area-averaged rainfall depth over a mid-size basin from two remote sensing methods of estimating precipitation. In Predictions in Ungauged Basins: PUB Kick-Off, Proceedings of the PUB Kick-Off Meeting Held in Brasilia, 20–22 November 2002; IAHS Publ.: London, UK, 2007. [Google Scholar]
- Huffman, G.J.; Bolvin, D.; Nelkin, E.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The trmm multisatellite precipitation analysis (tmpa): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. Cmorph: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.L.; Gao, X.; Gupta, H.V.; Imam, B.; Dan, B. Evaluation of persiann system satellite–based estimates of tropical rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; Iwanami, K. Global precipitation map using satellite-borne microwave radiometers by the gsmap project: Production and validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Ushio, T.; Sasashige, K.; Kubota, T.; Shige, S.; Okamoto, K.I.; Aonashi, K.; Inoue, T.; Takahashi, N.; Iguchi, T.; Kachi, M.; et al. A kalman filter approach to the global satellite mapping of precipitation (gsmap) from combined passive microwave and infrared radiometric data. J. Meteorol. Soc. Jpn. 2009, 87A, 137–151. [Google Scholar] [CrossRef]
- Mei, Y.; Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Evaluating satellite precipitation error propagation in runoff simulations of mountainous basins. J. Hydrometeorol. 2016, 17, 1407–1423. [Google Scholar] [CrossRef]
- Chen, F.; Li, X. Evaluation of imerg and trmm 3b43 monthly precipitation products over mainland China. Remote Sens. 2016, 8, 472. [Google Scholar] [CrossRef]
- Ning, S.; Wang, J.; Jin, J.; Ishidaira, H. Assessment of the latest gpm-era high-resolution satellite precipitation products by comparison with observation gauge data over the Chinese mainland. Water 2016, 8, 481. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of gpm day-1 imerg and tmpa version-7 legacy products over mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of integrated multi-satellite retrievals for global precipitation measurement over China. Atmos. Res. 2016, 176–177, 121–133. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Eylander, J.B.; Joyce, R.J.; Huffman, G.J.; Adler, R.F.; Hsu, K.L.; Turk, F.J.; Garcia, M.; Zeng, J. Component analysis of errors in satellite-basd precipitation estimates. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Xu, S.; Shen, Y.; Du, Z. Tracing the source of the errors in hourly imerg using a decomposition evaluation scheme. Atmosphere 2016, 7, 161. [Google Scholar] [CrossRef]
- Ning, S.; Song, F.; Udmale, P.; Jin, J.; Thapa, B.R.; Ishidaira, H. Error analysis and evaluation of the latest gsmap and imerg precipitation products over eastern China. Adv. Meteorol. 2017, 2017, 1803492. [Google Scholar] [CrossRef]
- Yong, B.; Chen, B.; Tian, Y.; Yu, Z.; Hong, Y. Error-component analysis of trmm-based multi-satellite precipitation estimates over mainland China. Remote Sens. 2016, 8, 440. [Google Scholar] [CrossRef]
- Meng, L.; Long, D.; Quiring, S.M.; Shen, Y. Statistical analysis of the relationship between spring soil moisture and summer precipitation in east China. Int. J. Climatol. 2014, 34, 1511–1523. [Google Scholar] [CrossRef]
- Yang, Y.; Yi, L. Evaluating the performance of remote sensing precipitation products cmorph, persiann, and tmpa, in the arid region of northwest China. Theor. Appl. Climatol. 2014, 118, 429–445. [Google Scholar] [CrossRef]
- Guo, Z.H.; Liu, X.M.; Xiao, W.F. Regionalization and integrated assessment of climate resource in China based on gis. Resour. Sci. 2007, 29, 2–9. (In Chinese) [Google Scholar]
- Shen, Y.; Zhao, P.; Pan, Y.; Yu, J. A high spatiotemporal gauge-satellite merged precipitation analysis over China. J. Geophys. Res. Atmos. 2014, 119, 3063–3075. [Google Scholar] [CrossRef] [Green Version]
- Xie, P.; Yatagai, A.; Chen, M.; Hayasaka, T.; Fukushima, Y.; Liu, C.; Yang, S. A gauge-based analysis of daily precipitation over East Asia. J. Hydrometeorol. 2007, 8, 607. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.; Wang, Y.; Xie, P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Feng, M.; Zhang, H.; Gao, F. Interpolation methods of China daily precipitation data. J. Appl. Meteorol. Sci. 2010, 21, 279–286. (In Chinese) [Google Scholar]
- Shen, Y.; Xiong, A. Validation and comparison of a new gauge-based precipitation analysis over mainland China. Int. J. Climatol. 2016, 36, 252–265. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Ma, M.; Liu, R.; Wen, Y.; Hong, Y. Can near-real-time satellite precipitation products capture rainstorms and guide flood warning for the 2016 summer in south China? IEEE Geosci. Remote Sens. Lett. 2017. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.; Hong, Y.; Yu, J.; Pan, Y.; Chen, Z.; Saharia, M. Uncertainty analysis of five satellite-based precipitation products and evaluation of three optimally merged multi-algorithm products over the tibetan plateau. Int. J. Remote Sens. 2014, 35, 6843–6858. [Google Scholar] [CrossRef]
- Karaseva, M.O.; Prakash, S.; Gairola, R.M. Validation of high-resolution trmm-3b43 precipitation product using rain gauge measurements over kyrgyzstan. Theor. Appl. Climatol. 2012, 108, 147–157. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. Algorithm Theoretical Basis Document (ATBD) Version 5.1. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V5.1b.pdf (accessed on 22 January 2018).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Integrated Multi-satellitE Retrievals for GPM (IMERG) Technical Documentation. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_doc_171117b.pdf (accessed on 22 January 2018).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Stocker, E.F.; Tan, J. V05 Imerg Final Run Release Notes; NASA/GSFC: Greenbelt, MD, USA, 2017.
- Omranian, E.; Sharif, H.O. Evaluation of the global precipitation measurement (GPM) satellite rainfall products over the lower Colorado River Basin, Texas. JAWRA J. Am. Water Resour. Assoc. 2018. [Google Scholar] [CrossRef]
- Okamoto, K.I.; Ushio, T.; Iguchi, T.; Takahashi, N.; Iwanami, K. The global satellite mapping of precipitation (gsmap) project. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 29 July 2005; pp. 3414–3416. [Google Scholar]
- Maggioni, V.; Meyers, P.C.; Robinson, M.D. A review of merged high-resolution satellite precipitation product accuracy during the tropical rainfall measuring mission (TRMM) era. J. Hydrometeorol. 2016, 17. [Google Scholar] [CrossRef]
- Aonashi, K.; Liu, G.; Awaka, J.; Hirose, M.; Kozu, T.; Kubota, T.; Shige, S.; Kida, S.; Seto, S.; Takahashi, N. Gsmap passive microwave precipitation retrieval algorithm: Algorithm description and validation. J. Meteorol. Soc. Jpn. 2009, 87A, 119–136. [Google Scholar] [CrossRef]
- Ushio, T.; Kachi, M. Kalman Filtering Applications for Global Satellite Mapping of Precipitation (GSMAP); Springer: Dordrecht, The Netherlands, 2010; pp. 105–123. [Google Scholar]
- Tian, Y.; Peterslidard, C.D.; Choudhury, B.J.; Garcia, M. Multitemporal analysis of trmm-based satellite precipitation products for land data assimilation applications. J. Hydrometeorol. 2007, 8, 1165–1183. [Google Scholar] [CrossRef]
- Wang, W.; Chen, X.; Shi, P.; Phajmvan, G. Detecting changes in extreme precipitation and extreme streamflow in the dongjiang river basin in southern China. Hydrol. Earth Syst. Sci. 2008, 12, 207–221. [Google Scholar] [CrossRef]
- Dinku, T.; Ceccato, P.; Grover-Kopec, E.; Lemma, M.; Connor, S.J.; Ropelewski, C.F. Validation of satellite rainfall products over East Africa’s complex topography. Int. J. Remote Sens. 2007, 28, 1503–1526. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.; Hong, Y. Multi-scale evaluation of high-resolution multi-sensor blended global precipitation products over the Yangtze River. J. Hydrol. 2013, 500, 157–169. [Google Scholar] [CrossRef]
- Omranian, E.; Sharif, H.O.; Tavakoly, A.A. How well can global precipitation measurement (GPM) capture hurricanes? Case study: Hurricane harvey. Remote Sens. 2018, 10, 1150. [Google Scholar] [CrossRef]
- Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the version-6 and version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic extr. J. Hydrol. 2014, 508, 77–87. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Win, K.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Assessment of GPM and TRMM multi-satellite precipitation products in streamflow simulations in a data-sparse mountainous watershed in myanmar. Remote Sens. 2017, 9, 302. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; Dijk, A.I.J.M.V.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 23 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. Discuss. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J.E.; Michaelides, S. Precipitation: Measurement, remote sensing, climatology and modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Sun, R.; Yuan, H.; Liu, X.; Jiang, X. Evaluation of the latest satellite–gauge precipitation products and their hydrologic applications over the huaihe river basin. J. Hydrol. 2016, 536, 302–319. [Google Scholar] [CrossRef]
- Mega, T.; Ushio, T.; Kubota, T.; Kachi, M.; Aonashi, K.; Shige, S. Gauge adjusted global satellite mapping of precipitation (gsmap_gauge). In Proceedings of the General Assembly and Scientific Symposium, Florence, Italy, 9–14 November 2014; pp. 1–4. [Google Scholar]
- Yong, B.; Ren, L.; Hong, Y.; Gourley, J.J.; Tian, Y.; Huffman, G.J.; Chen, X.; Wang, W.; Wen, Y. First evaluation of the climatological calibration algorithm in the real-time tmpa precipitation estimates over two basins at high and low latitudes. Water Resour. Res. 2013, 49, 2461–2472. [Google Scholar] [CrossRef]
- Shen, Y.; Pan, Y.; Yu, J.J.; Zhao, P.; Zhou, Z.J. Quality assessment of hourly merged precipitation product over China. Trans. Atmos. Sci. 2013, 36, 37–46. (In Chinese) [Google Scholar]
- Su, X.; Shum, C.K.; Luo, Z. Evaluating imerg v04 final run for monitoring three heavy rain events over mainland China in 2016. IEEE Geosci. Remote Sens. Lett. 2018, 15, 444–448. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the gpm imerg satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, S.; You, S.; Huang, Y.; Wang, Q.; Zhou, Q. Comprehensive evaluation of two successive v3 and v4 imerg final run precipitation products over mainland China. Remote Sens. 2017, 10, 34. [Google Scholar] [CrossRef]
- Wei, G.; Lü, H.; Crow, W.T.; Zhu, Y.; Wang, J.; Su, J. Evaluation of satellite-based precipitation products from imerg v04a and v03d, cmorph and tmpa with gauged rainfall in three climatologic zones in China. Remote Sens. 2017, 10, 30. [Google Scholar] [CrossRef]
- Crow, W.T.; Berg, M.J.V.D.; Huffman, G.J.; Pellarin, T. Correcting rainfall using satellite-based surface soil moisture retrievals: The soil moisture analysis rainfall tool (smart). Water Resour. Res. 2011, 47, 2924–2930. [Google Scholar] [CrossRef]
- Lü, H.; Crow, W.T.; Zhu, Y.; Ouyang, F.; Su, J. Improving streamflow prediction using remotely-sensed soil moisture and snow depth. Remote Sens. 2016, 8, 503. [Google Scholar] [CrossRef]











| Statistic Metrics | Equation | Unit | Rang | Perfect Value |
|---|---|---|---|---|
| Correlation Coefficient (CC) | NA | 0~1 | 1 | |
| Root Mean Square Error (RMSE) | mm | 0~+∞ | 0 | |
| Relative bias (Rbias) | % | −∞~+∞ | 0 | |
| Mean Absolute Error (MAE) | mm | 0~+∞ | 0 |
| Satellite Products | |||
|---|---|---|---|
| Rain: 1 | No rain: 0 | ||
| Gauged Observations | Rain: 1 | Hit | Missed |
| No rain: 0 | False | 0 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, J.; Lü, H.; Zhu, Y.; Wang, X.; Wei, G. Component Analysis of Errors in Four GPM-Based Precipitation Estimations over Mainland China. Remote Sens. 2018, 10, 1420. https://doi.org/10.3390/rs10091420
Su J, Lü H, Zhu Y, Wang X, Wei G. Component Analysis of Errors in Four GPM-Based Precipitation Estimations over Mainland China. Remote Sensing. 2018; 10(9):1420. https://doi.org/10.3390/rs10091420
Chicago/Turabian StyleSu, Jianbin, Haishen Lü, Yonghua Zhu, Xiaoyi Wang, and Guanghua Wei. 2018. "Component Analysis of Errors in Four GPM-Based Precipitation Estimations over Mainland China" Remote Sensing 10, no. 9: 1420. https://doi.org/10.3390/rs10091420
APA StyleSu, J., Lü, H., Zhu, Y., Wang, X., & Wei, G. (2018). Component Analysis of Errors in Four GPM-Based Precipitation Estimations over Mainland China. Remote Sensing, 10(9), 1420. https://doi.org/10.3390/rs10091420