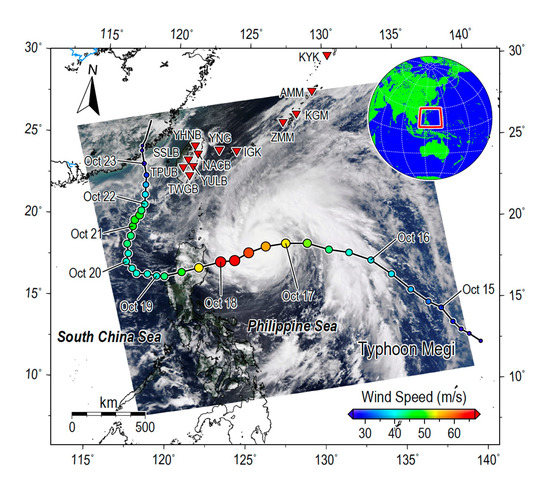
Seismological Observations of Ocean Swells Induced by Typhoon Megi Using Dispersive Microseisms Recorded in Coastal Areas
Abstract
:1. Introduction
2. Data
3. Methods
3.1. Location and Timing of Swell Origin
3.2. Fractional Fourier Transform
4. Results and Discussion
4.1. Swell-Generated DF Microseisms
4.2. Origins of Typhoon-Induced Swell
4.3. Localization Deviations
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Snodgrass, F.E.; Groves, G.W.; Hasselmann, K.; Miller, G.R.; Munk, W.H.; Powers, W.H. Propagation of ocean swell across the Pacific. Philos. Trans. R. Soc. Lond. Ser. A 1966, 249, 431–497. [Google Scholar] [CrossRef]
- Ardhuin, F.; Chapron, B.; Collard, F. Observation of swell dissipation across oceans. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef] [Green Version]
- Grachev, A.A.; Fairall, C.W. Upward momentum transfer in the marine boundary layer. J. Phys. Oceanogr. 2001, 31, 1698–1711. [Google Scholar] [CrossRef]
- Babanin, A.V. On a wave-induced turbulence and a wave-mixed upper ocean layer. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Hwang, P.A. Observations of swell influence on ocean surface roughness. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Semedo, A. Atmosphere-Ocean Interactions in Swell Dominated Wave Fields. Available online: http://www.diva-portal.org/smash/record.jsf?pid=diva2%3A350126&dswid=4604 (accessed on 6 September 2018).
- Wu, L.; Rutgersson, A.; Sahlee, E.; Guo Larsen, X. Swell impact on wind stress and atmospheric mixing in a regional coupled atmosphere-wave model. J. Geophys. Res. Oceans 2016, 121, 4633–4648. [Google Scholar] [CrossRef] [Green Version]
- Smedman, A.S.; Högström, U.; Sahleé, E.; Drennan, W.M.; Kahma, K.K.; Pettersson, H.; Zhang, F. Observational study of marine atmospheric boundary layer characteristics during swell. J. Atmos. Sci. 2009, 66, 2747–2763. [Google Scholar] [CrossRef]
- Högström, U.; Smedman, A.S.; Semedo, A.; Rutgersson, A. Comments on “A global climatology of wind-wave interaction”. J. Phys. Oceanogr. 2011, 41, 1811–1813. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.A.; Yang, X.; Pichel, W.G.; DeMaria, M.; Long, D.; Li, Z. Tropical cyclone morphology from spaceborne synthetic aperture radar. Bull. Am. Meteorol. Soc. 2012, 94, 215–230. [Google Scholar] [CrossRef]
- Li, X. The first Sentinel-1 SAR image of a typhoon. Acta Oceanol. Sin. 2015, 34. [Google Scholar] [CrossRef]
- Li, X.; Pichel, W.G.; He, M.; Wu, S.; Friedman, K.S.; Clemente-Colon, P.; Zhao, C. Observation of hurricane-generated ocean swell refraction at the Gulf Stream north wall with the RADARSAT-1 synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2131–2142. [Google Scholar]
- Jiang, H.; Stopa, J.E.; Wang, H.; Husson, R.; Mouche, A.; Chapron, B.; Chen, G. Tracking the attenuation and nonbreaking dissipation of swells using altimeters. J. Geophys. Res. Oceans 2016, 121, 1446–1458. [Google Scholar] [CrossRef] [Green Version]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Gartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Meansurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Dtsch. Hydrogr. Z. Suppl. 1973, 12, 1–95. [Google Scholar]
- Bromirski, P.D.; Flick, R.E.; Graham, N. Ocean wave height determined from inland seismometer data: Implications for investigating wave climate changes in the NE Pacific. J. Geophys. Res. Oceans 1999, 104, 20753–20766. [Google Scholar] [CrossRef] [Green Version]
- Okal, E.A.; MacAyeal, D.R. Seismic recording on drifting icebergs: Catching seismic waves, tsunamis and storms from Sumatra and elsewhere. Seismol. Res. Lett. 2006, 77, 659–671. [Google Scholar] [CrossRef]
- Barruol, G.; Reymond, D.; Fontaine, F.R.; Hyvernaud, O.; Maurer, V.; Maamaatuaiahutapu, K. Characterizing swells in the southern Pacific from seismic and infrasonic noise analyses. Geophys. J. Int. 2006, 164, 516–542. [Google Scholar] [CrossRef] [Green Version]
- Barruol, G.; Davy, C.; Fontaine, F.R.; Schlindwein, V.; Sigloch, K. Monitoring austral and cyclonic swells in the “Iles Eparses” (Mozambique channel) from microseismic noise. Acta Oecol. 2016, 72, 120–128. [Google Scholar] [CrossRef] [Green Version]
- Cathles IV, L.M.; Okal, E.A.; MacAyeal, D.R. Seismic observations of sea swell on the floating Ross Ice Shelf, Antarctica. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Davy, C.; Barruol, G.; Fontaine, F.R.; Cordier, E. Analyses of extreme swell events on La Réunion Island from microseismic noise. Geophys. J. Int. 2016, 207, 1767–1782. [Google Scholar] [CrossRef] [Green Version]
- Haubrich, R.A.; McCamy, K. Microseisms: Coastal and pelagic sources. Rev. Geophys. 1969, 7, 539–571. [Google Scholar] [CrossRef]
- Bromirski, P.D. Vibrations from the “Perfect Storm”. Geochem. Geophy. Geosyst. 2001, 2. [Google Scholar] [CrossRef] [Green Version]
- Bromirski, P.D.; Duennebier, F.K.; Stephen, R.A. Mid-ocean microseisms. Geochem. Geophy. Geosyst. 2005, 6. [Google Scholar] [CrossRef] [Green Version]
- Longuet-Higgins, M.S. A theory of the origin of microseisms. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1950, 243, 1–35. [Google Scholar] [CrossRef]
- Gerstoft, P.; Fehler, M.C.; Sabra, K.G. When Katrina hit California. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Gerstoft, P.; Shearer, P.M.; Harmon, N.; Zhang, J. Global P, PP, and PKP wave microseisms observed from distant storms. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Gerstoft, P.; Bromirski, P.D. Pelagic and coastal sources of P-wave microseisms: Generation under tropical cyclones. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Lin, J.M.; Lin, J.; Xu, M. Microseisms generated by super typhoon Megi in the western Pacific Ocean. J. Geophys. Res. Oceans 2017, 122, 9518–9529. [Google Scholar] [CrossRef]
- Tanimoto, T.; Lin, C.J.; Hadziioannou, C.; Igel, H.; Vernon, F. Estimate of Rayleigh-to-Love wave ratio in the secondary microseism by a small array at Piñon Flat observatory, California. Geophys. Res. Lett. 2016, 43. [Google Scholar] [CrossRef]
- Nishida, K.; Takagi, R. Teleseismic S wave microseisms. Science 2016, 353, 919–921. [Google Scholar] [CrossRef] [PubMed]
- Hasselmann, K.A. Statistical analysis of the generation of microseisms. Rev. Geophys. 1963, 1, 177–210. [Google Scholar] [CrossRef]
- Webb, S.C. Broadband seismology and noise under the ocean. Rev. Geophys. 1998, 36, 105–142. [Google Scholar] [CrossRef] [Green Version]
- Ardhuin, F.; Stutzmann, E.; Schimmel, M.; Mangeney, A. Ocean wave sources of seismic noise. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Chi, W.C.; Chen, W.J.; Kuo, B.Y.; Dolenc, D. Seismic monitoring of western Pacific typhoons. Mar. Geophys. Res. 2010, 31, 239–251. [Google Scholar] [CrossRef] [Green Version]
- Sufri, O.; Koper, K.D.; Burlacu, R.; Foy, B.D. Microseisms from Superstorm Sandy. Earth Planet. Sci. Lett. 2014, 402, 324–336. [Google Scholar] [CrossRef]
- Lin, J.M.; Wang, Y.T.; Wang, W.T.; Li, X.F.; Fang, S.K.; Chen, C.; Zheng, H. Seismic Remote Sensing of Super Typhoon Lupit (2009) with Seismological Array Observation in NE China. Remote Sens. 2018, 10, 235. [Google Scholar] [CrossRef]
- Gray, W.M. Global view of the origin of tropical disturbances and storms. Mon. Weather Rev. 1968, 96, 669–700. [Google Scholar] [CrossRef]
- Lu, X.; Yu, H.; Yang, X.; Li, X. Estimating tropical cyclone size in the Northwestern Pacific from geostationary satellite infrared images. Remote Sens. 2017, 9, 728. [Google Scholar] [CrossRef]
- Munk, W.H.; Miller, G.R.; Snodgrass, F.E.; Barber, N.F. Directional recording of swell from distant storms. Philos. Trans. R. Soc. Lond. Ser. A 1963, 255, 505–584. [Google Scholar] [CrossRef]
- Namias, V. The fractional order Fourier transform and its application to quantum mechanics. IMA J. Appl. Math. 1980, 25, 241–265. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, L.; Liu, K.; Liu, D. Separation and localization of multiple distributed wideband chirps using the fractional Fourier transform. EURASIP J. Wirel. Commun. Netw. 2015, 1, 1–8. [Google Scholar] [CrossRef]
- Wei, D.; Li, Y.M. Generalized sampling expansions with multiple sampling rates for lowpass and bandpass signals in the fractional Fourier transform domain. IEEE Trans. Signal Process. 2016, 64, 4861–4874. [Google Scholar] [CrossRef]
- Capus, C.; Brown, K. Short-time fractional Fourier methods for the time-frequency representation of chirp signals. J. Acoust. Soc. Am. 2003, 113, 3253–3263. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, A.; Kruger, F.; Klinge, K. Ocean generated microseismic noise located with the Gräfenberg array. J. Seismolog. 1998, 2, 47–64. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F. New improved version of Generic Mapping Tools released. EOS Trans. AGU 1998, 79, 579. [Google Scholar] [CrossRef]








© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, J.; Fang, S.; Li, X.; Wu, R.; Zheng, H. Seismological Observations of Ocean Swells Induced by Typhoon Megi Using Dispersive Microseisms Recorded in Coastal Areas. Remote Sens. 2018, 10, 1437. https://doi.org/10.3390/rs10091437
Lin J, Fang S, Li X, Wu R, Zheng H. Seismological Observations of Ocean Swells Induced by Typhoon Megi Using Dispersive Microseisms Recorded in Coastal Areas. Remote Sensing. 2018; 10(9):1437. https://doi.org/10.3390/rs10091437
Chicago/Turabian StyleLin, Jianmin, Sunke Fang, Xiaofeng Li, Renhao Wu, and Hong Zheng. 2018. "Seismological Observations of Ocean Swells Induced by Typhoon Megi Using Dispersive Microseisms Recorded in Coastal Areas" Remote Sensing 10, no. 9: 1437. https://doi.org/10.3390/rs10091437
APA StyleLin, J., Fang, S., Li, X., Wu, R., & Zheng, H. (2018). Seismological Observations of Ocean Swells Induced by Typhoon Megi Using Dispersive Microseisms Recorded in Coastal Areas. Remote Sensing, 10(9), 1437. https://doi.org/10.3390/rs10091437