A 55-Year Time Series Station for Primary Production in the Adriatic Sea: Data Correction, Extraction of Photosynthesis Parameters and Regime Shifts
Abstract
:1. Introduction
2. Materials and Methods
2.1. Production Measurements
2.2. Estimating Daily Production at Depth
3. Results
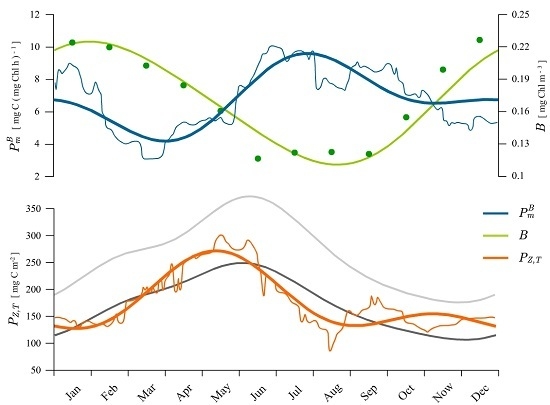
3.1. Correcting Historical Daily Production Estimates
3.2. Estimating Water Column Production
3.3. Regime Shifts
3.4. Remote Sensing Application
4. Discussion
4.1. Recovered Assimilation Numbers
4.2. Remotely-Sensed Chlorophyll
4.3. Long-Term Changes
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barber, R.T.; Hilting, A.K. History of the study of plankton productivity. In Phytoplankton Productivity—Carbon Assimilation in Marine and Freshwater Ecosystems; Blackwell Science: Hoboken, NJ, USA, 2002; pp. 16–43. [Google Scholar]
- Steemann Nielsen, E. The use of radioactive carbon (14C) for measuring organic production in the sea. Journal du Conseil International pour l’Exploration de la Mer 1952, 18, 117–140. [Google Scholar] [CrossRef]
- Karl, D.M.; Lukas, R. The Hawaii Ocean Time-series (HOT) program: Background, rationale and field implementation. Deep-Sea Res. II 1996, 43, 129–156. [Google Scholar] [CrossRef]
- Steinberg, D.K.; Carlson, C.A.; Bates, N.R.; Johnson, R.J.; Michaels, A.F.; Knap, A.H. Overview of the US JGOFS Bermuda Atlantic Time-series Study (BATS): a decade-scale look at ocean biology and biogeochemistry. Deep-Sea Res. II 2001, 48, 1405–1447. [Google Scholar] [CrossRef]
- Marasović, I.; Grbec, B.; Morović, M. Long-term production changes in the Adriatic. Neth. J. Sea Res. 1995, 34, 267–273. [Google Scholar] [CrossRef]
- Marasović, I.; Ninčević, Z.; Kušpilić, G.; Marinović, S.; Marinov, S. Long-term changes of basic biological and chemical parameters at two stations in the middle Adriatic. J. Sea Res. 2005, 54, 3–14. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S. Fundamental issues in measurement of primary production. ICES Mar. Sci. Symp. 1993, 197, 3–8. [Google Scholar]
- Peterson, B.J. Aquatic primary production and the 14C-CO2 method: A history of the productivity problem. Annu. Rev. Ecol. Evol. Syst. 1980, 11, 359–385. [Google Scholar] [CrossRef]
- Kovač, Z.; Platt, T.; Sathyendranath, S.; Morović, M.; Jackson, T. Recovery of photosynthesis parameters from in situ profiles of phytoplankton production. ICES J. Mar. Sci. 2016, 73, 275–285. [Google Scholar] [CrossRef]
- Ryther, J.H. Photosynthesis and Fish Production in the Sea. Science 1969, 166, 72–76. [Google Scholar] [CrossRef] [PubMed]
- Grbec, B.; Morović, M.; Beg Paklar, G.; Kušpilić, G.; Matijević, S.; Matić, F.; Ninčević Gladan, Ž. The relationship between the atmospheric variability and productivity in the Adriatic Sea area. J. Mar. Biol. Assoc. UK 2009, 89, 1549–1558. [Google Scholar] [CrossRef]
- Ninčević, Z.; Marasović, I.; Grbec, B.; Skejić, S.; Bužančić, M.; Kušpilić, G.; Matijević, S.; Matić, F. Inter-decadal variability in phytoplankton community in the Middle Adriatic (Kaštela Bay) in relation to the North Atlantic Oscillation. Estuaries Coasts 2010, 33, 376–383. [Google Scholar] [CrossRef]
- Williams, P.J.L. On the definition of plankton production terms. ICES Mar. Sci. Symp. 1993, 197, 9–19. [Google Scholar]
- Lizon, F.; Lagadeuc, Y. Comparisons of primary production values estimated from different incubation times in a coastal sea. J. Plankton Res. 1998, 20, 371–381. [Google Scholar] [CrossRef] [Green Version]
- Platt, T.; Sathyendranath, S.; White, G.N.; Jackson, T.; Saux Picart, S.; Bouman, H. Primary Production: Sensitivity to Surface Irradiance and Implications for Archiving Data. Front. Mar. Sci. 2017, 4, 387. [Google Scholar] [CrossRef]
- Platt, T.; Gallegos, C.L.; Harrison, W.G. Photoinhibition of photosynthesis in natural assemblages of marine phytoplahnkton. J. Mar. Res. 1980, 38, 687–701. [Google Scholar]
- Lohrenz, S.E. Fundamental issues in measurement of primary production. ICES Mar. Sci. Symp. 1993, 197, 159–171. [Google Scholar]
- Ryther, J.H. Photosynthesis in the Ocean as a Function of Light Intensity. Limnol. Oceanogr. 1956, 1, 61–69. [Google Scholar] [CrossRef]
- Kovač, Z.; Platt, T.; Sathyendranath, S.; Morović, M. Analytical solution for the vertical profile of daily production in the ocean. J. Geophys. Res. Oceans 2016, 121, 3532–3548. [Google Scholar] [CrossRef]
- Strickland, J.D.H.; Parsons, T.R. A Practical Handbook on Seawater Analysis; Fisheries Research Board of Canada: Ottawa, ON, Canada, 1972; p. 167. [Google Scholar]
- Matić, F.; Kovač, Z.; Vilibić, I.; Mihanović, H.; Morović, M.; Grbec, B.; Leder, N.; Džoić, T. Oscillating Adriatic temperature and salinity regimes mapped using the Self-Organizing Maps method. Cont. Shelf Res. 2017, 132, 11–18. [Google Scholar] [CrossRef]
- Grasshoff, K.; Ehrhardt, M.; Kremling, K. Methods of Sea Water Analysis, 2nd ed.; Verlag Chemie: Weinheim, Germany, 1983; p. 419. [Google Scholar]
- Jassby, A.D.; Platt, T. Mathematical formulation of the relationship between photosynthesis and light for phytoplankton. Limnol. Oceanogr. 1976, 21, 540–547. [Google Scholar] [CrossRef] [Green Version]
- Platt, T.; Jassby, A. The relationship between photosynthesis and light for natural assemblages of coastal marine phytoplankton. J. Phycol. 1976, 12, 421–430. [Google Scholar] [CrossRef]
- Kirk, J.T.O. Light and Photosynthesis in Quatic Ecosystems, 3rd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Platt, T.; Sathyendranath, S.; Ravindran, P. Primary Production by Phytoplankton: Analytic Solutions for Daily Rates per Unit Area of Water Surface. Proc. R. Soc. B 1990, 241, 101–111. [Google Scholar] [CrossRef]
- Kovač, Z.; Platt, T.; Antunović, S.; Sathyendranath, S.; Morović, M.; Gallegos, C. Extended Formulations and Analytic Solutions for Watercolumn Production Integrals. Front. Mar. Sci. 2017, 4, 163. [Google Scholar] [CrossRef]
- Rodionov, S.N. A sequential algorithm for testing climate regime shifts. Geophys. Res. Lett. 2004, 31, LO9204. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S. Oceanic primary production: Estimation by remote sensing at local and regional scales. Science 1988, 241, 1613–1620. [Google Scholar] [CrossRef] [PubMed]
- Platt, T.; Woods, J.D.; Sathyendranath, S.; Barkmann, W. Net Primary Production and Stratification in the Ocean. Geophys. Monogr. 1994, 85, 247–254. [Google Scholar]
- Platt, T.; Broomhead, D.S.; Sathyendranath, S.; Edwards, A.M.; Murphy, E.J. Phytoplankton biomass and residual nitrate in the pelagic ecosystem. Proc. R. Soc. A 2003, 459, 1063–1073. [Google Scholar] [CrossRef] [Green Version]
- Sathyendranath, S.; Brewin, B.; Mueller, D.; Doerffer, R.; Krasemann, H.; Mélin, F.; Brockmann, C.; Fomferra, N.; Peters, M.; Grant, M.; et al. Ocean Colour Climate Change Initiative; Approach and initial results. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 2024–2027. [Google Scholar]
- Sathyendranath, S.; Brewin, R.J.W.; Jackson, T.; Mélin, F.; Platt, T. Ocean-colour products for climate-change studies: What are their ideal characteristics? Remote Sens. Environ. 2017, 203, 125–138. [Google Scholar] [CrossRef]
- Jackson, T.; Sathyendranath, S.; Mélin, F. An improved optical classification scheme for the Ocean Colour Essential Climate Variable and its applications. Remote Sens. Environ. 2017, 203, 152–161. [Google Scholar] [CrossRef]
- MacIntyre, H.L.; Kana, T.M.; Anning, T.; Geider, R. Photoacclimation of photosynthesis irradiance response curves and photosynthetic pigments in microalge and cyanobacteria. J. Phycol. 2002, 38, 17–38. [Google Scholar] [CrossRef]
- Falkowski, P.G. Light-shade adaptation and assimilation numbers. J. Plankton Res. 1981, 3, 203–216. [Google Scholar] [CrossRef]
- Milligan, A.; Hasley, K.M.; Behrenfeld, M.J. Advancing interpretations of 14C-uptake measurements in the context of phytoplankton physiology and ecology. J. Plankton Res. 2015, 37, 692–698. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Wayne, E.E.; Turpie, K.R. Assessment of primary production at the global scale. In Phytoplankton Productivity—Carbon Assimilation in Marine and Freshwater Ecosystems; Blackwell Science: Hoboken, NJ, USA, 2002; pp. 78–108. [Google Scholar]
- Marra, J. Vertical mixing and primary production. In Primary Productivity in the Sea; Plenum Press: New York, NY, USA, 1980; pp. 121–137. [Google Scholar]
- Harris, G.P. Phytoplankton productivity and growth measurements: past, present and future. J. Plankton Res. 1984, 6, 219–237. [Google Scholar] [CrossRef]
- Jones, C.T.; Craig, S.E.; Barnett, A.B.; MacIntyre, H.L.; Cullen, J.J. Curvature in models of the photosynthesis-irradiance response. J. Phycol. 2014, 50, 341–355. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kovač, Z.; Platt, T.; Sathyendranath, S.; Antunović, S. Models for estimating photosynthesis parameters from in situ production profiles. Prog. Oceanogr. 2017, 159, 255–266. [Google Scholar] [CrossRef]
- Karl, D.M.; Bidigare, R.R.; Letelier, R.M. Sustained and aperiodic variability in organic matter production and phototrophic microbial community structure in the North Pacific Subtropical Gyre. In Phytoplankton Productivity—Carbon Assimilation in Marine And Freshwater Ecosystems; Blackwell Science: Hoboken, NJ, USA, 2002; pp. 78–108. [Google Scholar]
- Longhurst, A.R. Ecological Geography of the Sea, 2nd ed.; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Falkowski, P.G.; Owens, T.G. Light-shade adaptation: Two strategies in marine phytoplankton. Plant Physiol. 1980, 66, 592–595. [Google Scholar] [CrossRef] [PubMed]
- Harrison, W.G.; Platt, T. Variations in assimilation number of coastal marine phytophytoplankton: Effects of environmental co-variates. J. Plankton Res. 1980, 2, 249–260. [Google Scholar] [CrossRef]
- Renk, H.; Ochocki, S. Photosynthetic rate and light curves of phytoplankton in the southern Baltic. Oceanologia 1998, 40, 331–344. [Google Scholar]
- Takahashi, M.; Fugii, K.; Parsons, T. Simulation study of phytoplankton photosyn- thesis and growth in the Fraser River Estuary. Mar. Biol. 1973, 19, 102–116. [Google Scholar] [CrossRef]
- Marra, J.; Trees, C.C.; O’Reilly, J.E. Phytoplankton pigment absorption: A strong predictor of primary productivity in the surface ocean. Deep-Sea Res. I 2007, 54, 155–163. [Google Scholar] [CrossRef]
- Laws, E.A.; Redalje, D.G.; Haas, L.W.; Bienfang, P.; Eppley, R.W.; Harrison, W.G.; Karl, D.M.; Marra, J. High Phytoplankton Growth and Production-Rates in Oligotrophic Hawaiian Coastal Waters. Limnol. Oceanogr. 1984, 29, 1161–1169. [Google Scholar] [CrossRef]
- Videau, C.; Sournia, A.; Prieur, L.; Fiala, M. Phytoplankton and primary production characteristics at selected sites in the geostrophic Almeria-Oran front system (SW Mediterranean Sea). J. Mar. Syst. 1994, 5, 235–250. [Google Scholar] [CrossRef]
- Latasa, M.; Morán, X.A.G.; Scharek, R.; Estrada, M. Estimating the carbon flux through main phytoplankton groups in the northwestern Mediterranean. Limnol. Oceanogr. 2005, 50, 1447–1458. [Google Scholar] [CrossRef] [Green Version]
- Morán, G.X.A.; Estrada, M. Short-term variability of photosynthetic parameters and particulate and dissolved primary production in the Alboran Sea (SW Mediterranean). Mar. Ecol. Prog. Ser. 2001, 212, 53–67. [Google Scholar] [CrossRef] [Green Version]
- Gasol, J.M.; Cardelús, C.; Morán, X.A.G.; Balagué, V.; Forn, I.; Marrasé, C.; Massana, R.; Pedrós-Alió, C.; Montserrat Sala, M.; Simó, R.; et al. Seasonal patterns in phytoplankton photosynthetic parameters and primary production at a coastal NW Mediterranean site. Sci. Mar. 2016, 80, 63–77. [Google Scholar] [CrossRef] [Green Version]
- Kovač, Z.; Platt, T.; Sathyendranath, S.; Lomas, M.W. Extraction of photosynthesis parameters from time-series measurements of in situ production. Remote Sens. 2018, 10, 915. [Google Scholar] [CrossRef]
- Chavez, F.P.; Messié, M.; Pennington, J.T. Marine Primary Production in Relation to Climate Variability and Change. Annu. Rev. Mar. Sci. 2011, 3, 227–260. [Google Scholar] [CrossRef] [PubMed]
- Longhurst, A. Seasonal cycles of pelagic production and consumption. Prog. Oceanogr. 1995, 36, 77–167. [Google Scholar] [CrossRef]
- Ninčević, Z. Size-Fractionated Biomass in the Middle Adriatic. Ph.D. Thesis, University of Zagreb, Zagreb, Croatia, 2000. [Google Scholar]
- Ninčević, Z. Contribution of the Different Size Phytoplankton Categories in Biomass and Primary Production of the Middle Adriatic Sea. Master’s Thesis, University of Zagreb, Zagreb, Croatia, 1996. [Google Scholar]
- Kirk, J.T.O. Optical properties of picoplankton suspensions. Photosynth. Picoplankton 1986, 214, 501–520. [Google Scholar]
- Civitarese, G.; Gačić, M.; Lipizer, M.; Eusebi Borzelli, G.L. On the impact of the Bimodal Oscillating System (BiOS) on the biogeochemistry and biology of the Adriatic and Ionian Seas (Eastern Mediterranean). Biogeosciences 2010, 7, 3987–3997. [Google Scholar] [CrossRef] [Green Version]
- Jeffrey, S.W.; Mantoura, R.F.C.; Wright, S.W. Phytoplanton pigments in oceanography: guidlines to modern methods. In Monographs on Oceanographic Methodology; UNESCO Publishing: Paris, France, 1997; pp. 1–661. [Google Scholar]
- Morović, M.; Flander Puterle, V.; Lučić, D.; Grbec, B.; Gangai, B.; Malej, A.; Matić, F. Signatures of pigments and processes in the south Adriatic Pit-project MEDUZA. Acta Adriatica 2012, 53, 303–322. [Google Scholar]
- Jerlov, N.G. Marine Optics, 2nd ed.; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Morović, M.; Precali, R. Comparison of Satellite Colour Data to in Situ Chlorophyll Measurements. Int. J. Remote Sens. 2004, 25, 1507–1516. [Google Scholar] [CrossRef]
- Grbec, B.; Morović, M. Seasonal thermohaline fluctuations in the Middle Adriatic Sea. Il Nuovo Cimento 1997, 20, 561–576. [Google Scholar]
- Vilibić, I.; Book, J.W.; Beg Paklar, G.; Orlić, M.; Dadić, V.; Tudor, M.; Martin, P.J.; Pasarić, M.; Grbec, B.; Matić, F.; et al. West Adriatic coastal water summertime excursion into the East Adriatic. J. Mar. Syst. 2008, 78, S132–S156. [Google Scholar] [CrossRef]
- Buljan, M. Fluctuations of Salinity in the Adriatic; Reports; Institut za Oceanografiju i Ribarstvo: Split, Croatia, 1953; Volume 2, p. 64. [Google Scholar]
- Vilibić, I.; Matijević, J.; Šepić, J.; Kušpilić, G. Changes in the Adriatic oceanographic properties induced by the Eastern Mediterranean Transient. Biogeosciences 2012, 9, 2085–2097. [Google Scholar] [CrossRef] [Green Version]
- Gačić, M.; Eusebi Borzelli, G.L.; Civitarese, G.; Cardin, V.; Yari, S. Can internal processes sustain reversals of the ocean upper circulation? The Ionian Sea example. Geophys. Res. Lett. 2010, 37, L09608. [Google Scholar] [CrossRef]







| No. | Duration | B | T | DIN | DIP | ||
|---|---|---|---|---|---|---|---|
| 1 | 1962–1979 | 118 ± 21 | - | - | 16.2 ± 2.8 | 2.04 ± 0.99 | 0.072 ± 0.023 |
| 2 ↑ | 1979–1997 | 214 ± 24 | 4.9 ± 4.1 | 0.19 ± 0.02 | 15.9 ± 3.0 | 1.99 ± 1.24 | 0.072 ± 0.048 |
| 3 ↓ | 1997–2008 | 128 ± 20 | 5.1 ± 3.8 | 0.11 ± 0.03 | 16.7 ± 3.0 | 1.67 ± 1.31 | 0.068 ± 0.058 |
| 4 ↑ | 2008–2013 | 251 ± 22 | 4.5 ± 2.6 | 0.21 ± 0.02 | 16.5 ± 3.2 | 1.23 ± 0.86 | 0.062 ± 0.082 |
| 5 ↓ | 2013–now | 154 ± 23 | 4.9 ± 4.3 | 0.17 ± 0.01 | 16.8 ± 2.8 | 1.55 ± 0.79 | 0.058 ± 0.046 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovač, Ž.; Platt, T.; Ninčević Gladan, Ž.; Morović, M.; Sathyendranath, S.; Raitsos, D.E.; Grbec, B.; Matić, F.; Veža, J. A 55-Year Time Series Station for Primary Production in the Adriatic Sea: Data Correction, Extraction of Photosynthesis Parameters and Regime Shifts. Remote Sens. 2018, 10, 1460. https://doi.org/10.3390/rs10091460
Kovač Ž, Platt T, Ninčević Gladan Ž, Morović M, Sathyendranath S, Raitsos DE, Grbec B, Matić F, Veža J. A 55-Year Time Series Station for Primary Production in the Adriatic Sea: Data Correction, Extraction of Photosynthesis Parameters and Regime Shifts. Remote Sensing. 2018; 10(9):1460. https://doi.org/10.3390/rs10091460
Chicago/Turabian StyleKovač, Žarko, Trevor Platt, Živana Ninčević Gladan, Mira Morović, Shubha Sathyendranath, Dionysios E. Raitsos, Branka Grbec, Frano Matić, and Jere Veža. 2018. "A 55-Year Time Series Station for Primary Production in the Adriatic Sea: Data Correction, Extraction of Photosynthesis Parameters and Regime Shifts" Remote Sensing 10, no. 9: 1460. https://doi.org/10.3390/rs10091460
APA StyleKovač, Ž., Platt, T., Ninčević Gladan, Ž., Morović, M., Sathyendranath, S., Raitsos, D. E., Grbec, B., Matić, F., & Veža, J. (2018). A 55-Year Time Series Station for Primary Production in the Adriatic Sea: Data Correction, Extraction of Photosynthesis Parameters and Regime Shifts. Remote Sensing, 10(9), 1460. https://doi.org/10.3390/rs10091460