Data Processing and Interpretation of Antarctic Ice-Penetrating Radar Based on Variational Mode Decomposition
Abstract
:1. Introduction
2. Variational Mode Decomposition Method Principle
3. Processing Non-Stationary, Nonlinear Synthetic Data and Simulated Ice-Penetrating Radar Data with VMD
3.1. Comparison of VMD and EMD Tests for Synthetic Data
3.2. Processing Simulated Ice-Penetrating Radar Data with VMD
3.2.1. Ice-Penetrating Radar Forward Simulation
3.2.2. Processing Simulated Data with VMD
4. Processing and Interpretation of Antarctic Ice-Penetrating Radar Data
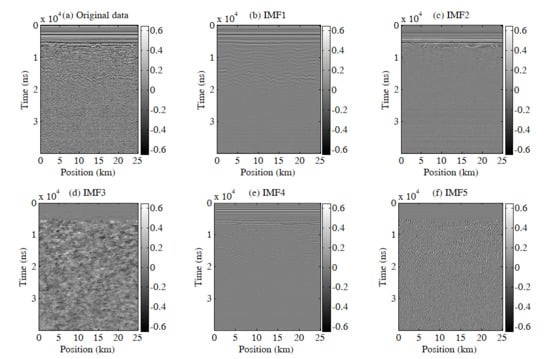
4.1. Analysis and Processing of Antarctic Ice-Penetrating Radar Data
4.2. Interpretation of Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qin, D.H.; Kang, S.C. Present process of glacier and global climatic and environmental change. Earth Sci. Front. 1997, 4, 85–94. (In Chinese) [Google Scholar]
- Allison, I.; Alley, R.B.; Fricker, H.A.; Thomas, R.H.; Warner, R.C. Ice sheet mass balance and sea level. Antarct. Sci. 2009, 21, 413–426. [Google Scholar] [CrossRef] [Green Version]
- Deconto, R.M.; Pollard, D. Contribution of Antarctica to past and future sea-level rise. Nature 2016, 531, 591–597. [Google Scholar] [CrossRef]
- Zhang, X.P.; Sun, B.; Wang, B.B.; Tang, X.Y.; Tian, G. Radar Detection of Characteristics and Distribution of Isochronous Ice Layer in Antarctic Ice Sheet. In Proceedings of the Chinese Geophysical Society Annual Conference, Hangzhou, China, 15–19 October 2006. (In Chinese). [Google Scholar]
- Shepherd, A.; Ivins, E.R.; Rignot, E.; Smith, B.; Broeke, M.R.V.D.; Velicogna, I.; Whitehouse, P.L.; Briggs, K.; Joughin, I.; Krinner, G.; et al. Mass balance of the Antarctic Ice Sheet from 1992 to 2017. Nature 2018, 558, 219–222. [Google Scholar] [Green Version]
- Evans, S. Radio techniques for the measurement of ice thickness. Pol. Rec. 1963, 11, 406–410. [Google Scholar] [CrossRef]
- Plewes, L.A.; Hubbard, B. A review of the use of radio-echo sounding in glaciology. Prog. Phys. Geogr. 2001, 25, 203–236. [Google Scholar] [CrossRef]
- Bogorodskiy, V.V.; Bentley, C.R.; Gudmandsen, P. Radioglaciology; Kluwer: Dordrecht, The Netherlands, 1985. [Google Scholar]
- Cui, X.B.; Sun, B.; Zhang, X.P.; Zhang, D.; Li, X.; Tang, X.; Tian, G. A review of ice radar’s technical development in polar ice sheet investigation. Chin. J. Polar Res. 2009, 21, 322–335. (In Chinese) [Google Scholar]
- Bingham, R.G.; Siegert, M.J. Radio-echo sounding over polar ice masses. J. Environ. Eng. Geophys. 2007, 12, 47–62. [Google Scholar] [CrossRef]
- Tzanis, A. Detection and extraction of orientation-and-scale-dependent information from two-dimensional GPR data with tuneable directional wavelet filters. J. Appl. Geophys. 2013, 89, 48–67. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Gonçalvès, P. On empirical mode decomposition and its algorithms. In Proceedings of the IEEE-Eurasip Workshop Nonlinear Signal Image Process, c(NSIP), Trieste, Italy, 8–11 June 2003; Volume 3, pp. 8–11. [Google Scholar]
- Wang, T. Research on EMD Algorithm and Its Application in Signal Denoising; Harbin Engineering University: Harbin, China, 2010. (In Chinese) [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Partyka, G.; Gridley, J.; Lopez, J. Interpretational applications of spectral decomposition in reservoir characterization. Lead. Edge 1999, 18, 353–360. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, A.; Okaya, D. Frequency-time decomposition of seismic data using wavelet-based methods. Geophysics 1995, 60, 1906–1916. [Google Scholar] [CrossRef]
- Odebeatu, E.; Zhang, J.; Chapman, M.; Liu, E.; Li, X.Y. Application of spectral decomposition to detection of dispersion anomalies associated with gas saturation. Lead. Edge 2006, 25, 206–210. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, X. Spectral decomposition using Wigner-Ville distribution with applications to carbonate reservoir characterization. Lead. Edge 2008, 27, 1050–1057. [Google Scholar] [CrossRef]
- Wang, Y.H.; Yeh, C.H.; Young, H.W.V.; Hu, K.; Lo, M.T. On the computational complexity of the empirical mode decomposition algorithm. Phys. A Stat. Mech. Its Appl. 2014, 400, 159–167. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, F.Z.; Li, J.; Lin, J.; Hu, Y.; Wang, X.; Sun, X. Simulation of the Lunar Regolith and Lunar-Penetrating Radar Data Processing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 655–663. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, F.Z.; Li, J.; Hu, Z.; Zhang, J. Lunar Penetrating Radar Data Processing and Analysis Based on CEEMD. In Proceedings of the 2018 17th International Conference on Ground Penetrating Radar (GPR), Rapperswil, Switzerland, 18–21 June 2018. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Two-dimensional variational mode decomposition. Energy Minimization Methods Comput. Vis. Pattern Recognit. 2015, 8932, 197–208. [Google Scholar]
- Xue, Y.J.; Cao, J.X.; Wang, D.X.; Du, H.K.; Yao, Y. Application of the Variational-Mode Decomposition for Seismic Time–frequency Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 9, 3821–3831. [Google Scholar] [CrossRef]
- Zhang, X.; Nilot, E.; Feng, X.; Ren, Q.; Zhang, Z. IMF-Slices for GPR Data Processing Using Variational Mode Decomposition Method. Remote Sens. 2018, 10, 476. [Google Scholar] [CrossRef]
- Hoeher, P.A.; Kaiser, S.; Robertson, P. Two-dimensional pilot-symbol-aided channel estimation by Wiener filtering. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Munich, Germany, 21–24 April 1997; pp. 1845–1848. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J. A non-local algorithm for image denoising. Comput. Vis. Pattern Recogn. 2005, 2, 60–65. [Google Scholar]
- Feng, D.S.; Chen, C.S.; Yu, K. Signal Enhancement and Complex Signal Analysis of GPR Based on Hilbert-Huang Transform. Lect. Notes Electr. Eng. 2011, 99, 375–384. [Google Scholar]
- Daubechies, I.; Lu, J.; Wu, H.-T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef] [Green Version]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Rockafellar, R.T. A dual approach to solving nonlinear programming problems by unconstrained optimization. Math. Program 1973, 5, 354–373. [Google Scholar] [CrossRef] [Green Version]
- Bertsekas, D.P. Constrained optimization and Lagrange Multiplier methods. In Computer Science and Applied Mathematics; Academic Pr: Boston, MA, USA, 1982; Volume 1. [Google Scholar]
- MacGregor, J.A.; Winebrenner, D.P.; Conway, H.; Matsuoka, K.; Mayewski, P.A.; Clow, G.D. Modeling englacial radar attenuation at Siple Dome, West Antarctica, using ice chemistry and temperature data. J. Geophys. Res. Earth Surf. 2007, 112, 1–14. [Google Scholar] [CrossRef]
- Liu, S.X.; Zeng, Z.F.; Xu, B. FDTD Simulation of Ground Penetrating Radar Signal in 3-Dimensional Dispersive Medium. J. Jilin Univ. (Earth Sci. Ed.) 2006, 36, 123–127. (In Chinese) [Google Scholar]
- Li, J.; Zeng, Z.F.; Wu, F.S.; Lin, H. Study of three dimension high-order FDTD simulation for GPR. Chin. J. Geophys. 2010, 53, 974–981. (In Chinese) [Google Scholar]
- Feng, D.S.; Chen, C.S.; Dai, Q.W. GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD. Chin. J. Geophys. 2010, 53, 2484–2496. (In Chinese) [Google Scholar]
- Cui, X.B.; Wang, T.T.; Sun, B.; Tang, X.; Guo, J. Chinese radioglaciological studies on the Antarctic ice sheet: Progress and prospects. Adv. Polar Sci. 2017, 28, 161–170. [Google Scholar]
- Jacobel, R.W.; Hodge, S.M. Radar Internal Layers from the Greenland Summit. Geophys. Res. Lett. 1995, 22, 587–590. [Google Scholar] [CrossRef]
- Fujita, S.; Maeno, H.; Uratsuka, S.; Furukawa, T.; Mae, S.; Fujii, Y.; Watanabe, O. Nature of radio echo layering in the Antarctic ice sheet detected by a two-frequency experiment. J. Geophys. Res. Solid Earth 1999, 104, 13013–13024. [Google Scholar] [CrossRef]
- Yang, S.H.; Gu, Q.M.; Yun, Y.; Cui, X.B.; Tang, X.Y. A review of the use of ice penetrating radar to diagnose the subglacial environments. Chin. J. Polar Res. 2016, 28, 277–286. (In Chinese) [Google Scholar]
- Tang, X.Y.; Sun, B.; Cui, X.B. Review of research progress of internal radar isochronous layers in Antarctic ice sheet. Chin. J. Polar Res. 2015, 27, 104–114. (In Chinese) [Google Scholar]
- Vaughan, D.G.; Anderson, P.S.; King, J.C.; Mann, G.W.; Mobbs, S.D.; Ladkin, R.S. Imaging of firn isochrones across an Antarctic ice rise and implications for patterns of snow accumulation rate. J. Glaciol. 2004, 50, 413–418. [Google Scholar] [CrossRef]
- Eisen, O.; Nixdorf, U.; Wilhelms, F.; Miller, H. Age estimates of isochronous reflection horizons by combining ice core, survey, and synthetic radar data. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Herron, M.M.; Langway, C.C. Firn densification: An empirical model. J. Glaciol. 1980, 25, 373–385. [Google Scholar] [CrossRef]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers, 4th ed.; Academic Press: Cambridge, MA, USA, 2010; pp. 11–25. [Google Scholar]
- Grima, C.; Blankenship, D.D.; Young, D.A.; Schroeder, D.M. Surface slope control on firn density at Thwaites Glacier, West Antarctica: Results from airborne radar sounding. Geophys. Res. Lett. 2014, 41, 6787–6794. [Google Scholar] [CrossRef]

















| Composition | Interface | Average Depth of the Interface (m) | Ice Inner Layer | Average Relative Permittivity ɛr | Average Conductivity σ(s/m) |
|---|---|---|---|---|---|
| Air | - | - | 1 | 0 | |
| Air ice interface | 0 | ||||
| Ice sheet | I | 3.00 | 0.00001 | ||
| Ice inner layer interface 1 | 5 | ||||
| II | 3.07 | 0.00004 | |||
| Ice inner layer interface 2 | 10 | ||||
| III | 3.15 | 0.00006 | |||
| Ice rock interface | 17.5 | ||||
| Bedrock | - | 6 | 0.00018 | ||
| - | |||||
| IMFs | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 |
|---|---|---|---|---|---|
| Correlation Coefficient | 0.5059 | 0.6375 | 0.3841 | 0.3529 | 0.7839 |
| IMFs | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 |
|---|---|---|---|---|---|
| Correlation Coefficient | 0.6313 | 0.2996 | 0.2230 | 0.6819 | 0.2412 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, S.; Liu, S.; Guo, J.; Luo, K.; Zhang, L.; Tang, X. Data Processing and Interpretation of Antarctic Ice-Penetrating Radar Based on Variational Mode Decomposition. Remote Sens. 2019, 11, 1253. https://doi.org/10.3390/rs11101253
Cheng S, Liu S, Guo J, Luo K, Zhang L, Tang X. Data Processing and Interpretation of Antarctic Ice-Penetrating Radar Based on Variational Mode Decomposition. Remote Sensing. 2019; 11(10):1253. https://doi.org/10.3390/rs11101253
Chicago/Turabian StyleCheng, Siyuan, Sixin Liu, Jingxue Guo, Kun Luo, Ling Zhang, and Xueyuan Tang. 2019. "Data Processing and Interpretation of Antarctic Ice-Penetrating Radar Based on Variational Mode Decomposition" Remote Sensing 11, no. 10: 1253. https://doi.org/10.3390/rs11101253
APA StyleCheng, S., Liu, S., Guo, J., Luo, K., Zhang, L., & Tang, X. (2019). Data Processing and Interpretation of Antarctic Ice-Penetrating Radar Based on Variational Mode Decomposition. Remote Sensing, 11(10), 1253. https://doi.org/10.3390/rs11101253