A Convolutional Neural Network with Fletcher–Reeves Algorithm for Hyperspectral Image Classification
Abstract
:1. Introduction
2. Materials and Research Area
2.1. Hyperspectral Data
2.2. Supplementary Data
2.3. Study Area Introduction
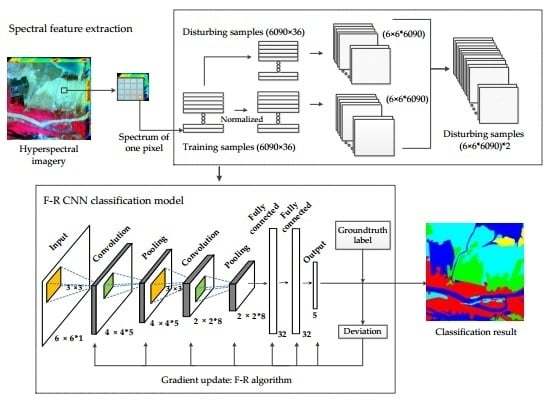
3. Proposed Method
3.1. Input Processing
3.2. Mathematical Knowledge
3.3. F–R CNN Model
| Gradient update of F–R algorithm: | |
| 1 | Completing the forward propagation process: initialize the weight W and offset b of each layer l to obtain the prediction result h. |
| 2 | Calculating the error between the predicted results and the real results by the cost function J. |
| 3 | Finding the first-order partial derivatives and and calculate and of each hidden layer l in reverse. |
| 4 | If the number of iterations is i = 1, the descending direction of each layer is the first-order partial derivative , and is , and then go to step 6. |
| 5 | If the number of iterations i = 2, 3..., the descending direction of each layer is calculated according to Equation (10) and is calculated from Equation (11). |
| 6 | Substituting and into Equations (8) and (9), the weights and offset of each layer are calculated, and the parameter update is completed. |
| 7 | Performing the next forward propagation until the cost function J converges or reaches the maximum number of iterations. |
4. Experimental Results and Discussion
4.1. Dataset and Experimental Settings
4.1.1. Dataset Description
4.1.2. Experimental Settings
4.2. Experiment Results
4.3. Discussion
4.3.1. Increase Training Samples
4.3.2. Adjust the Disturbance Magnitude
4.3.3. Change the Number of Batch Training Samples
4.3.4. Iteration Time
4.4. Additional Application of the Proposed Method
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sainath, T.N.; Kingsbury, B.; Saon, G.; Soltau, H.; Mohamed, A.; Dahl, G.; Ramabhadran, B. Deep Convolutional Neural Networks for large-scale speech tasks. Neural Netw. 2015, 64, 39–48. [Google Scholar] [CrossRef] [PubMed]
- Swietojanski, P.; Ghoshal, A.; Renals, S. Convolutional Neural Networks for Distant Speech Recognition. IEEE Signal Process. Lett. 2014, 21, 1120–1124. [Google Scholar] [Green Version]
- Wei, Y.; Xia, W.; Lin, M.; Huang, J.; Ni, B.; Dong, J.; Zhao, Y.; Yan, S. HCP: A Flexible CNN Framework for Multi-Label Image Classification. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1901–1907. [Google Scholar] [CrossRef] [PubMed]
- Zha, S.X.; Luisier, F.; Andrews, W.; Srivastava, N.; Salakhutdinov, R. Exploiting Image-trained CNN Architectures for Unconstrained Video Classification. In Proceedings of the British Machine Vision Conference (BMVC), Swansea, UK, 7–10 September 2015; p. 60. [Google Scholar]
- Zhang, X.; Zhao, J.B.; Lecun, Y. Character-level Convolutional Networks for Text Classification. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 649–657. [Google Scholar]
- Peng, J.T.; Du, Q. Robust joint sparse representation based on maximum correntropy criterion for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7152–7164. [Google Scholar] [CrossRef]
- Dong, Y.N.; Du, B.; Zhang, L.P.; Zhang, L.F. Dimensionality reduction and classification of hyperspectral images using ensemble discriminative local metric learning. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2509–2524. [Google Scholar] [CrossRef]
- Paul, S.; Nagesh Kumar, D. Spectral-spatial classification of hyperspectral data with mutual information based segmented stacked autoencoder approach. ISPRS J. Photogramm. Remote Sens. 2018, 138, 265–280. [Google Scholar] [CrossRef]
- Lin, Z.H.; Chen, Y.S.; Zhao, X.; Wang, G. Spectral-spatial classification of hyperspectral image using autoencoders. In Proceedings of the 9th International Conference on Information, Communications & Signal Processing (ICICS), Tainan, Taiwan, 10–13 December 2013; pp. 1–5. [Google Scholar]
- Zhou, P.C.; Han, J.W.; Cheng, G.; Zhang, B.C. Learning compact and discriminative stacked autoencoder for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, in press. [Google Scholar] [CrossRef]
- Tao, C.; Pan, H.B.; Li, Y.S.; Zou, Z.R. Unsupervised spectral-spatial feature learning with stacked sparse autoencoder for hyperspectral imagery Classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2438–2442. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, Y.W.; Wang, W.Q.; Gao, W. Content-Based Natural Image Classification and Retrieval Using SVM. Chin. J. Comput. 2003, 26, 1261–1265. [Google Scholar]
- Tan, K.; Du, P.J. Hyperspectral remote sensing image classification based on support vector machine. J. Infrared Millim. Waves 2008, 27, 123–128. [Google Scholar] [CrossRef]
- Du, P.J.; Lin, H.; Sun, D.X. On Progress of Support Vector Machine Based Hyperspectral RS Classification. Bull. Surv. Mapp. 2006, 12, 37–40. [Google Scholar]
- Chen, S.J.; Pang, Y.F. High resolution remote sensing image classificatoin based on Boosting and Bagging algorithms. Sci. Surv. Mapp. 2010, 35, 169–172. [Google Scholar]
- Du, X.X. Boosting Algorithm Based Research in Face Recognition Methods. Ph.D. Dissertation, Zhejiang University, Zhejiang, China, 2006. [Google Scholar]
- Feng, D.; Wenkang, S.; Liangzhou, C.; Yong, D.; Zhenfu, Z. Infrared image segmentation with 2-D maximum entropy method based on particle swarm optimization (PSO). Pattern Recognit. Lett. 2005, 26, 597–603. [Google Scholar] [CrossRef]
- Castelluccio, M.; Poggi, G.; Sansone, C.; Verdoliva, L. Land Use Classification in Remote Sensing Images by Convolutional Neural Networks. Acta Ecol. Sin. 2015, 28, 627–635. [Google Scholar]
- Hu, F.; Xia, G.S.; Hu, J.W.; Zhang, L.P. Transferring Deep Convolutional Neural Networks for the Scene Classification of High-Resolution Remote Sensing Imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef] [Green Version]
- Kussul, N.; Lavreniuk, M.; Skakun, S.; Shelestov, A. Deep Learning Classification of Land Cover and Crop Types Using Remote Sensing Data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 778–782. [Google Scholar] [CrossRef]
- Li, E.Z.; Xia, J.S.; Du, P.J.; Lin, C.; Samat, A. Integrating Multilayer Features of Convolutional Neural Networks for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5653–5665. [Google Scholar] [CrossRef]
- Sharma, A.; Liu, X.W.; Yang, X.J.; Shi, D. A patch-based convolutional neural network for remote sensing image classification. Neural Netw. 2017, 95, 19–28. [Google Scholar] [CrossRef]
- Zhu, J.; Fang, L.Y.; Ghamisi, P. Deformable Convolutional Neural Networks for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1254–1258. [Google Scholar] [CrossRef]
- Chen, C.Y.; Gong, W.G.; Chen, Y.L.; Li, W.H. Object Detection in Remote Sensing Images Based on a Scene-Contextual Feature Pyramid Network. Remote Sens. 2019, 11, 339. [Google Scholar] [CrossRef]
- Fang, B.; Li, Y.; Zhang, H.K.; Chan, J.C.W. Hyperspectral Images Classification Based on Dense Convolutional Networks with Spectral-Wise Attention Mechanism. Remote Sens. 2019, 11, 159. [Google Scholar] [CrossRef]
- Chen, Y.S.; Jiang, H.L.; Li, C.Y.; Jia, X.P.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.Z.; Du, S.H. Spectral–spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Chen, C.C.; Jiang, F.; Yang, C.F.; Rho, S.; Shen, W.Z.; Liu, S.H.; Liu, Z.G. Hyperspectral classification based on spectral–spatial convolutional neural networks. Eng. Appl. Artif. Intell. 2018, 68, 165–171. [Google Scholar] [CrossRef]
- Li, Y.S.; Xie, W.Y.; Li, H.Q. Hyperspectral image reconstruction by deep convolutional neural network for classification. Pattern Recognit. 2017, 63, 371–383. [Google Scholar] [CrossRef]
- Yue, J.; Zhao, W.Z.; Mao, S.J.; Liu, H. Spectral–spatial classification of hyperspectral images using deep convolutional neural networks. Remote Sens. Lett. 2015, 6, 468–477. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.D.; Zhang, F.; Du, Q. Hyperspectral Image Classification Using Deep Pixel-Pair Features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Zhang, M.M.; Li, W.; Du, Q. Diverse Region-Based CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2018, 27, 2623–2634. [Google Scholar] [CrossRef]
- Cheng, G.; Li, Z.P.; Han, J.W.; Yao, X.W.; Guo, L. Exploring hierarchical convolutional features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6712–6722. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. A new deep convolutional neural network for fast hyperspectral image classification. ISPRS J. Photogramm. Remote Sens. 2017, 145, 120–147. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Zhong, Z.L.; Li, J.; Luo, Z.M.; Chapman, M. Spectral-Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2017, 56, 847–858. [Google Scholar] [CrossRef]
- Shi, C.; Pun, C.M. Superpixel-based 3D deep neural networks for hyperspectral image classification. Pattern Recognit. 2018, 74, 600–616. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference for Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 1–13. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the 30th International Conference on Machine Learning (ICML’13), Atlanta, GA, USA, 16–21 June 2013; pp. 1139–1147. [Google Scholar]
- Botev, A.; Lever, G.; Barber, D. Nesterov’s accelerated gradient and momentum as approximations to regularised update descent. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1899–1903. [Google Scholar]
- Andrychowicz, M.; Denil, M.; Gomez, S.; Hoffman, M.W.; Pfau, D.; Schaul, T.; Shillingford, B.; de Freitas, N. Learning to learn by gradient descent by gradient descent. In Proceedings of the 30th Conference on Neural Information Processing Systems (NIPS 2016), Barcelona, Spain, 18 August 2016; pp. 748–756. [Google Scholar]
- Sarigül, M.; Avci, M. Performance comparison of different momentum techniques on deep reinforcement learning. J. Inf. Telecommun. 2018, 2, 205–216. [Google Scholar] [CrossRef] [Green Version]
- Yue, Q.; Ma, C.W. Deep Learning for Hyperspectral Data Classification through Exponential Momentum Deep Convolution Neural Networks. J. Sens. 2016, 2016, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Su, W.J.; Boyd, S.; Candes, E.J. A Differential Equation for Modeling Nesterov’s Accelerated Gradient Method: Theory and Insights. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2510–2518. [Google Scholar]
- Zhang, X.H.; Saha, A.; Vishwanathan, S.V.N. Regularized Risk Minimization by Nesterov’s Accelerated Gradient Methods: Algorithmic Extensions and Empirical Studies. arXiv 2010, arXiv:1011.0472. [Google Scholar]
- Chen, Z.Y.; Xing, X.S.; Li, Y. Implement of Conjugate Gradient BP Algorithm in Matlab 7.0. Mod. Electron. Tech. 2009, 32, 125–127. [Google Scholar]
- Fletcher, R.; Reeves, C.M. Function minimization by conjugate gradients. Comput. J. 1964, 7, 149–154. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.L.; Chan, J.C.W.; Canters, F. Fully Automatic Subpixel Image Registration of Multiangle CHRIS/Proba Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2829–2839. [Google Scholar]
- Chen, B.L. Optimization Theory and Algorithm, 2nd ed.; Tsinghua University Press: Beijing, China, 2005; pp. 281–301. [Google Scholar]
- Bottou, L. Large-Scale Machine Learning with Stochastic Gradient Descent. In Proceedings of the COMPSTAT’2010, Paris, France, 22–27 August 2010; pp. 177–186. [Google Scholar]
- Nakama, T. Theoretical analysis of batch and on-line training for gradient descent learning in neural networks. Neurocomputing 2009, 73, 151–159. [Google Scholar] [CrossRef]
- Qian, Q.; Jin, R.; Yi, J.F.; Zhang, L.J.; Zhou, S.H. Efficient distance metric learning by adaptive sampling and mini-batch stochastic gradient descent (SGD). Mach. Learn. 2015, 99, 353–372. [Google Scholar] [CrossRef]













| Parameter | Index |
|---|---|
| Spatial sampling interval /m | End of the sky 18 |
| Image area/km × km | 14 × 14 |
| Number of images | 5(different angles) |
| Image size/km | 13 × 13(768 × 748pixels) |
| Each image size/Mbit | 131 |
| Pixel format | BSQ |
| Spectral range /nm | 400–1050 |
| Data unit | MicroWatts/nm/m2/str |
| Number of spectral bands | 18 bands with a spatial resolution of 17 m, 62 bands with 34 m |
| Spectral resolution | 1.3 nm@410 nm to 12 nm@1050 nm |
| Signal to noise ratio | 200 |
| No. | Color | Type | Pattern | Feature |
|---|---|---|---|---|
| 1 |  | Reed |  | Hi-wet, tall grass that can be wet for many years, can grow in fresh or salt water. |
| 2 |  | Mixture of Suaeda-salsa and tamarisk |  | The halophyte, which is high in humidity and salt-tolerant, grows on sand or sandy loam in coastal areas such as seashores and wastelands, and is sparsely distributed. Tamarix is a salt-tolerant shrub that grows on sand, silt and tidal flats such as beaches, beachheads, coasts, and is resistant to dry and watery, wind and alkali resistant. |
| 3 |  | Water |  | The river section near the Yellow River mouth. |
 | Naturally formed or manually excavated pit water surface for aquaculture. | |||
| 4 |  | Spartina alterniflora |  | Plants resistant to salt and flooding, born in intertidal zone. |
| 5 |  | Tidal flats and bare land |  | This paper refers to the muddy tidal flat, the tide intrusion zone between the high tide level and the low tide level. |
| Layers | Layer Name | Image Size | Size of Kernels | No. of Kernels | Pool Scale |
|---|---|---|---|---|---|
| 1 | Input | 6 * 6 | - | - | - |
| 2 | Convolution | 4 * 4 * 5 | 3*3 | 5 | - |
| 3 | Pooling | 4 * 4 * 5 | 1*1 | - | 1 |
| 4 | Convolution | 2 * 2 * 8 | 3*3 | 8 | - |
| 5 | Pooling | 2 * 2 * 8 | 1*1 | - | 1 |
| 6 | Fully connected | 32 * 1 | - | - | - |
| 7 | Fully connected | 32 * 1 | - | - | - |
| 8 | Output | 5 * 1 | - | - | - |
| Class | Samples | |||
|---|---|---|---|---|
| No. | Color | Land Cover Types | Train | Test |
| 1 |  | Reed | 1468 | 66121 |
| 2 |  | Mixture of Suaeda-salsa and tamarisk | 1367 | 44811 |
| 3 |  | Water | 1531 | 64274 |
| 4 |  | Spartina alterniflora | 411 | 5926 |
| 5 |  | Tidal flats and bare land | 1313 | 80942 |
| Total | 6090 | 262144 | ||
| Training Samples | CNN(%) | Improved(%) | F-R CNN(%) | Improved(%) |
|---|---|---|---|---|
| 1x(original) | 83.34 | - | 82.89 | - |
| 4x | 82.96 | −0.38 | 83.16 | 0.27 |
| 8x | 83.54 | 0.20 | 84.15 | 1.26 |
| 12x | 84.56 | 1.22 | 83.67 | 0.78 |
| 16x | 82.61 | −0.73 | 82.79 | −0.10 |
| 20x | 83.47 | 0.13 | 82.74 | −0.15 |
| Training Set | 4x (%) | 8x (%) | 12x (%) | 16x (%) | 20x (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| CNN | FR-CNN | CNN | FR-CNN | CNN | FR-CNN | CNN | FR-CNN | CNN | FR-CNN | |
| A (1%) | 82.96 (−0.38) | 83.16 (+0.27) | 83.54 (+0.2) | 84.15 (+1.26) | 84.56 (+1.22) | 83.67 (+0.78) | 82.61 (−0.73) | 82.79 (−0.10) | 83.47 (+0.13) | 82.74 (−0.15) |
| B (2%) | 83.67 (+0.33) | 83.77 (+0.88) | 84.98 (+1.64) | 84.46 (+1.57) | 84.05 (+0.71) | 83.34 (+0.45) | 83.49 (+0.15) | 82.31 (−0.58) | 84.28 (+0.94) | 83.39 (+0.50) |
| C (3%) | 83.53 (+0.19) | 83.13 (+0.24) | 84.62 (+1.28) | 84.52 (+1.63) | 84.44 (+1.10) | 82.69 (−0.20) | 83.87 (+0.53) | 82.88 (−0.01) | 84.12 (+0.78) | 82.75 (−0.14) |
| D (4%) | 83.55 (+0.21) | 82.54 (−0.35) | 84.73 (+1.39) | 83.85 (+0.96) | 83.99 (+0.65) | 83.47 (+0.58) | 83.31 (−0.03) | 83.19 (+0.30) | 83.90 (+0.56) | 82.29 (−0.60) |
| E (5%) | 82.82 (−0.52) | 82.58 (−0.31) | 84.68 (+1.34) | 84.07 (+1.18) | 84.24 (+0.90) | 83.22 (+0.33) | 83.11 (−0.23) | 82.84 (−0.05) | 82.96 (−0.38) | 82.76 (+0.13) |
| Batch Size | A (1%) (%) | B (2%) (%) | C (3%) (%) | D (4%) (%) | E (5%) (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| CNN | FR-CNN | CNN | FR-CNN | CNN | FR-CNN | CNN | FR-CNN | CNN | FR-CNN | |
| 20 | 84.14 | 83.65 | 84.33 | 83.88 | 84.02 | 83.97 | 84.13 | 83.97 | 84.16 | 84.14 |
| 40 | 83.19 | 84.04 | 83.18 | 84.27 | 83.14 | 83.96 | 83.30 | 84.02 | 83.00 | 84.05 |
| 60 | 82.35 | 83.92 | 82.28 | 83.96 | 82.33 | 83.84 | 82.49 | 83.89 | 82.19 | 83.84 |
| 75 | 82.13 | 83.50 | 82.07 | 83.47 | 82.08 | 83.46 | 82.21 | 83.47 | 82.00 | 83.39 |
| 100 | 81.74 | 82.52 | 81.70 | 82.48 | 81.70 | 82.53 | 81.84 | 82.66 | 81.63 | 82.34 |
| 120 | 81.53 | 82.22 | 81.50 | 82.07 | 81.49 | 82.19 | 81.58 | 82.32 | 81.44 | 82.03 |
| 140 | 81.32 | 82.04 | 81.29 | 81.95 | 81.27 | 81.99 | 81.39 | 82.16 | 81.24 | 81.90 |
| 175 | 80.87 | 82.07 | 80.85 | 82.06 | 80.83 | 82.03 | 80.91 | 82.18 | 80.80 | 81.91 |
| 203 | 80.35 | 81.80 | 80.34 | 81.78 | 80.31 | 81.72 | 80.39 | 81.89 | 80.30 | 81.65 |
| 232 | 79.74 | 81.50 | 79.73 | 81.45 | 79.70 | 81.45 | 79.76 | 81.58 | 79.69 | 81.36 |
| 280 | 78.92 | 81.31 | 78.90 | 81.28 | 78.88 | 81.26 | 78.94 | 81.38 | 78.87 | 81.24 |
| 300 | 78.56 | 81.20 | 78.56 | 81.18 | 78.53 | 81.16 | 78.58 | 81.26 | 78.52 | 81.11 |
| 350 | 77.82 | 80.78 | 77.80 | 80.77 | 77.77 | 80.74 | 77.82 | 80.80 | 77.76 | 80.72 |
| 420 | 76.78 | 79.99 | 76.76 | 79.97 | 76.76 | 79.93 | 76.77 | 80.01 | 76.75 | 79.93 |
| 580 | 73.60 | 78.64 | 73.57 | 78.62 | 73.60 | 78.60 | 73.60 | 78.66 | 73.60 | 78.60 |
| CNN Batch Size | 10 | 20 | 50 | 120 | 150 | 280 | 300 |
|---|---|---|---|---|---|---|---|
| Iteration step | 200 | 200 | 200 | 200 | 200 | 200 | 200 |
| Number of steps with error rate <0.01 | 2 | 10 | 31 | 139 | 168 | - | - |
| Time of error rate <0.01 | 1.0 | 2.7 | 4.0 | 9.5 | 11.0 | - | - |
| Average iteration time per step | 0.50 | 0.27 | 0.13 | 0.07 | 0.07 | - | - |
| F-R CNN Batch Size | 10 | 20 | 50 | 120 | 150 | 280 | 300 |
| Iteration step | 200 | 200 | 200 | 200 | 200 | 200 | 200 |
| Number of steps with error rate <0.01 | 2 | 7 | 26 | 43 | 43 | 167 | - |
| Time of error rate <0.01 | 1.3 | 2.4 | 4.0 | 4.0 | 3.6 | 11.0 | - |
| Average iteration time per step | 0.64 | 0.34 | 0.16 | 0.09 | 0.08 | 0.07 | - |
| Class | Samples | ||
|---|---|---|---|
| No. | Land Cover Types | Train | Test |
| 1 | Asphalt | 332 | 6299 |
| 2 | Meadows | 933 | 17,716 |
| 3 | Gravel | 105 | 1994 |
| 4 | Trees | 154 | 2910 |
| 5 | Painted metal sheets | 68 | 1277 |
| 6 | Bare Soil | 252 | 4777 |
| 7 | Bitumen | 67 | 1263 |
| 8 | Self-Blocking Bricks | 185 | 3497 |
| 9 | Shadows | 48 | 899 |
| Method | CNN (%) | F-R CNN (%) | ||
|---|---|---|---|---|
| Training Set | Test Accuracy | Improved | Test Accuracy | Improved |
| 1X | 80.14 | - | 81.26 | - |
| 20X-A | 84.96 | 4.82 | 83.08 | 1.82 |
| 20X-B | 85.15 | 5.01 | 84.07 | 2.81 |
| 20X-C | 85.55 | 5.41 | 84.08 | 2.82 |
| 20X-D | 84.95 | 4.81 | 83.34 | 2.08 |
| 20X-E | 84.98 | 4.84 | 83.16 | 1.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Ma, Y.; Ren, G. A Convolutional Neural Network with Fletcher–Reeves Algorithm for Hyperspectral Image Classification. Remote Sens. 2019, 11, 1325. https://doi.org/10.3390/rs11111325
Chen C, Ma Y, Ren G. A Convolutional Neural Network with Fletcher–Reeves Algorithm for Hyperspectral Image Classification. Remote Sensing. 2019; 11(11):1325. https://doi.org/10.3390/rs11111325
Chicago/Turabian StyleChen, Chen, Yi Ma, and Guangbo Ren. 2019. "A Convolutional Neural Network with Fletcher–Reeves Algorithm for Hyperspectral Image Classification" Remote Sensing 11, no. 11: 1325. https://doi.org/10.3390/rs11111325
APA StyleChen, C., Ma, Y., & Ren, G. (2019). A Convolutional Neural Network with Fletcher–Reeves Algorithm for Hyperspectral Image Classification. Remote Sensing, 11(11), 1325. https://doi.org/10.3390/rs11111325