Registration Algorithm Based on Line-Intersection-Line for Satellite Remote Sensing Images of Urban Areas
Abstract
:1. Introduction
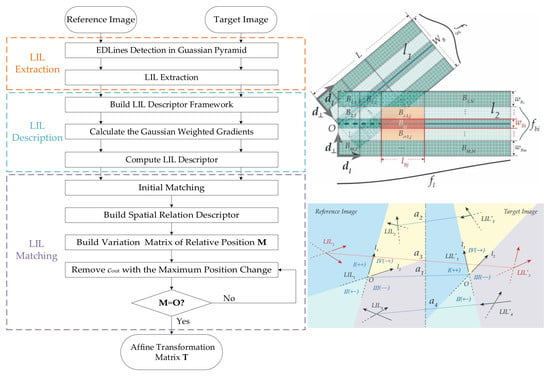
2. Methodology
2.1. LIL Feature Extraction and Description
2.1.1. Multi-scale LIL Feature Extraction
- Nearest-neighbor rectangular region search. Search other line segments in a rectangular region centered on line segment to compute intersections, as shown in Figure 3. Define the length of as ; then, set . The width and length of the rectangular region are and , respectively. The intersection is reserved when the starting or ending point of is within the rectangular region.
- Intersection angle constraint. The intersection angle of two line segments must satisfy .
- Distance constraint. The intersection may be on the segment extension line. If it is very far from the line segment, the positioning accuracy will be reduced and the intersection may not make sense; thus, the distance constraint is needed. The distance between and is defined as the distance between the midpoint of shorter line segment and their intersection, which must meet .
2.1.2. LIL Local Feature Description
2.2. LIL Matching
2.2.1. LIL Spatial Relation Descriptor
2.2.2. LIL Outlier Removal Based on LIL Spatial Relation Descriptor and Graph Theory
- Initialize with the unity vector, and .
- Compute the accumulated error and solve the match with the maximum error. The accumulated error of each match is obtained by summing each row of the variation matrix of relative position, and the matches corresponding to the maximum value can be solved as follows:where is the set of candidate removed matches. If , then return ; otherwise, set . More than one match may correspond to the maximum accumulated error. If , then the outlier is ; otherwise, these candidate matches should be compared by the number of matches whose position changes relative to them.where ⊕ is the xor symbol used to count the number of non-zero elements in the row corresponding to LIL match a.
- Remove match , and add it to . Delete the row and column in corresponding to , and set .
- Repeat Steps (2)and (3), until . Return , and add matches such that to .
| Algorithm 1 LIL Outlier Removal. |
Input: of size . Output: of size , of size , of size ,
|
3. Experiment and Results
3.1. Accuracy Evaluation
3.2. Parameter Setting
3.3. Experimental Results on Images with Simulated Transformations
3.3.1. Comparison of Matching Results with Different Methods
3.3.2. Comparison of SIFT and LIL Descriptor
3.4. Experimental Results on Real Multi-Temporal Remote Sensing Images
3.5. Comparison and Analysis of Outlier Filtering
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. In European Conference on Computer Vision; Springer: Berlin, Germany, 2006; pp. 404–417. [Google Scholar]
- Ke, Y.; Sukthankar, R. PCA-SIFT: A more distinctive representation for local image descriptors. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004. [Google Scholar]
- Morel, J.M.; Yu, G. ASIFT: A New Framework for Fully Affine Invariant Image Comparison. Siam J. Imaging Sci. 2010, 2, 438–469. [Google Scholar] [CrossRef]
- Sedaghat, A.; Mokhtarzade, M.; Ebadi, H. Uniform Robust Scale-Invariant Feature Matching for Optical Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4516–4527. [Google Scholar] [CrossRef]
- Dellinger, F.; Delon, J.; Gousseau, Y.; Michel, J.; Tupin, F. SAR-SIFT: A SIFT-like algorithm for SAR images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 453–466. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Aguilar, W.; Frauel, Y.; Escolano, F.; Martinez-Perez, M.E.; Espinosa-Romero, A.; Lozano, M.A. A robust graph transformation matching for non-rigid registration. Image Vis. Comput. 2009, 27, 897–910. [Google Scholar] [CrossRef]
- Liu, Z.; An, J.; Jing, Y. A simple and robust feature point matching algorithm based on restricted spatial order constraints for aerial image registration. IEEE Trans. Geosci. Remote Sens. 2012, 50, 514–527. [Google Scholar] [CrossRef]
- Zhang, K.; Li, X.Z.; Zhang, J.X. A Robust Point-Matching Algorithm for Remote Sensing Image Registration. IEEE Geosci. Remote Sens. Lett. 2013, 11, 469–473. [Google Scholar] [CrossRef]
- Alajlan, N.; El Rube, I.; Kamel, M.S.; Freeman, G. Shape retrieval using triangle-area representation and dynamic space warping. Pattern Recognit. 2007, 40, 1911–1920. [Google Scholar] [CrossRef]
- Shi, X.; Jiang, J. Point-matching method for remote sensing images with background variation. J. Appl. Remote Sens. 2015, 9, 095046. [Google Scholar] [CrossRef]
- Zhao, M.; An, B.; Wu, Y.; Luong, H.V.; Kaup, A. RFVTM: A Recovery and Filtering Vertex Trichotomy Matching for Remote Sensing Image Registration. IEEE Trans. Geosci. Remote Sens. 2017, 55, 375–391. [Google Scholar] [CrossRef]
- Von Gioi, R.G.; Jakubowicz, J.; Morel, J.M.; Randall, G. LSD: A fast line segment detector with a false detection control. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 722–732. [Google Scholar] [CrossRef] [PubMed]
- Akinlar, C.; Topal, C. EDLines: A real-time line segment detector with a false detection control. Pattern Recognit. Lett. 2011, 32, 1633–1642. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, F.; Hu, Z. MSLD: A robust descriptor for line matching. Pattern Recognit. 2009, 42, 941–953. [Google Scholar] [CrossRef]
- Zhang, L.; Koch, R. An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency. J. Vis. Commun. Image Represent. 2013, 24, 794–805. [Google Scholar] [CrossRef]
- Shi, X.; Jiang, J. Automatic Registration Method for Optical Remote Sensing Images with Large Background Variations Using Line Segments. Remote Sens. 2016, 8, 426. [Google Scholar] [CrossRef]
- Yammine, G.; Wige, E.; Simmet, F.; Niederkorn, D.; Kaup, A. Novel similarity-invariant line descriptor and matching algorithm for global motion estimation. IEEE Trans. Circuits Syst. Video Technol. 2014, 24, 1323–1335. [Google Scholar] [CrossRef]
- Long, T.; Jiao, W.; He, G.; Wang, W. Automatic line segment registration using Gaussian mixture model and expectation-maximization algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1688–1699. [Google Scholar] [CrossRef]
- Zhao, C.; Zhao, H.; Lv, J.; Sun, S.; Li, B. Multimodal image matching based on multimodality robust line segment descriptor. Neurocomputing 2016, 177, 290–303. [Google Scholar] [CrossRef]
- Jiang, J.; Cao, S.; Zhang, G.; Yuan, Y. Shape registration for remote-sensing images with background variation. Int. J. Remote Sens. 2013, 34, 5265–5281. [Google Scholar] [CrossRef]
- Yavari, S.; Zoej, M.J.V.; Salehi, B. An automatic optimum number of well-distributed ground control lines selection procedure based on genetic algorithm. ISPRS J. Photogramm. Remote Sens. 2018, 139, 46–56. [Google Scholar] [CrossRef]
- Fan, B.; Wu, F.; Hu, Z. Line matching leveraged by point correspondences. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 390–397. [Google Scholar]
- Zhao, M.; Wu, Y.; Pan, S.; Zhou, F.; An, B.; Kaup, A. Automatic Registration of Images With Inconsistent Content Through Line-Support Region Segmentation and Geometrical Outlier Removal. IEEE Trans. Image Process. 2018, 27, 2731–2746. [Google Scholar] [CrossRef] [PubMed]
- Sui, H.; Xu, C.; Liu, J.; Hua, F. Automatic optical-to-SAR image registration by iterative line extraction and Voronoi integrated spectral point matching. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6058–6072. [Google Scholar] [CrossRef]
- Li, K.; Yao, J.; Lu, X.; Li, L.; Zhang, Z. Hierarchical line matching based on Line-Junction-Line structure descriptor and local homography estimation. Neurocomputing 2016, 184, 207–220. [Google Scholar] [CrossRef]
- Lyu, C.; Jiang, J. Remote sensing image registration with line segments and their intersections. Remote Sens. 2017, 9, 439. [Google Scholar]
- Han, X.; Leung, T.; Jia, Y.; Sukthankar, R.; Berg, A.C. Matchnet: Unifying feature and metric learning for patch-based matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3279–3286. [Google Scholar]
- Kanazawa, A.; Jacobs, D.W.; Chandraker, M. Warpnet: Weakly supervised matching for single-view reconstruction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3253–3261. [Google Scholar]
- Rocco, I.; Arandjelovic, R.; Sivic, J. Convolutional neural network architecture for geometric matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; Volume 2. [Google Scholar]
- He, H.; Chen, M.; Chen, T.; Li, D. Matching of Remote Sensing Images with Complex Background Variations via Siamese Convolutional Neural Network. Remote Sens. 2018, 10, 355. [Google Scholar] [CrossRef]
- Yang, Z.; Dan, T.; Yang, Y. Multi-temporal Remote Sensing Image Registration Using Deep Convolutional Features. IEEE Access 2018, 6, 38544–38555. [Google Scholar] [CrossRef]
- Leordeanu, M.; Hebert, M. A Spectral Technique for Correspondence Problems Using Pairwise Constraints. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; pp. 1482–1489. [Google Scholar]















| Notation | Parameter | Default Value |
|---|---|---|
| Coefficient of search range | 0.5 | |
| Threshold of intersection angle constraint | ||
| Coefficient of distance constraint | 5 | |
| M | Number of rows of blocks in LSR | 9 |
| Widths of blocks | ||
| N | Number of columns of blocks in LSR | 4 |
| Separation column of coordinates | 2 | |
| Dimension of LIL local descriptor | 576 |
| Parameter Setting () | Total Correct Matches | Precision (%) | Descriptor Dimension |
|---|---|---|---|
| M = 7, | 8106 | 84.30 | 448 |
| M = 7, | 7716 | 84.96 | 448 |
| M = 7, | 7605 | 84.82 | 448 |
| M = 9, | 7992 | 84.61 | 576 |
| M = 9, | 7883 | 84.66 | 576 |
| M = 9, | 8483 | 85.39 | 576 |
| M = 11, | 8352 | 85.53 | 704 |
| M = 11, | 7687 | 85.03 | 704 |
| Parameter Setting | Total Correct Matches | Precision (%) | |
|---|---|---|---|
| N = 4 | = 1 | 8017 | 83.23 |
| = 2 | 8483 | 85.39 | |
| = 3 | 8247 | 84.60 | |
| = 4 | 8337 | 85.09 | |
| N = 3 | = 1 | 7726 | 83.64 |
| = 2 | 8083 | 84.74 | |
| = 3 | 8058 | 84.53 | |
| No. | Type | Location | Source | Date (yyyy/mm/dd) | Size | GSD |
|---|---|---|---|---|---|---|
| 1 | Years | Anqing, China | GoogleEarth | 2009/12/06 | 922*865 | 4 m |
| GoogleEarth | 2016/12/05 | 922*863 | 4 m | |||
| 2 | Hurricane | Seaside Heights, America | GeoEye-1 | 2010/09/07 | 1190*994 | 0.5 m |
| GeoEye-1 | 2012/10/31 | 1170*1002 | 0.5 m | |||
| 3 | Flooding | Nowshera, Pakistan | Quickbird | 2010/08/05 | 1888*1896 | 2 m |
| Quickbird | 2010/08/05 | 1888*1896 | 2 m | |||
| 4 | Seasons | Huhhot, China | GoogleEarth | 2017/01/20 | 1076*829 | 2 m |
| GoogleEarth | 2018/06/30 | 1076*829 | 2 m | |||
| 5 | Earthquake | Port-Au-Prince, Haiti | GeoEye-1 | 2010/01/13 | 2504*1884 | 0.5 m |
| IKONOS | 2008/09/29 | 1240*952 | 0.82 m | |||
| 6 | Tornado | Yazoo City, America | Quickbird | 2010/04/28 | 3432*2664 | 0.6 m |
| Quickbird | 2010/03/23 | 2992*2380 | 0.6 m |
| Algorithm | Evaluation | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| SIFT | TN | 170 | 112 | 140 | 82 | 283 | 25 |
| CN | 97 | 8 | 32 | 3 | 3 | 0 | |
| Precision (%) | 57.1 | 7.1 | 22.5 | 3.6 | 1.1 | 0 | |
| RMSE | 8.63 | 26.91 | 41.72 | — | — | — | |
| LP | TN | 7 | 48 | 20 | 4 | 4 | 1 |
| CN | 3 | 29 | 11 | 0 | 0 | 0 | |
| Precision (%) | 42.9 | 60.4 | 55.0 | 0 | 0 | 0 | |
| RMSE | 81.52 | 6.47 | 5.53 | — | — | — | |
| MSLD | TN | 6 | 8 | 20 | 5 | 1 | 11 |
| CN | 3 | 5 | 10 | 0 | 0 | 9 | |
| Precision (%) | 50 | 62.5 | 0 | 0 | 0 | 81.8 | |
| RMSE | 15.42 | 5.89 | 23.41 | — | — | — | |
| RLI | TN | 25 | 4 | 70 | 0 | 0 | 6 |
| CN | 17 | 2 | 70 | 0 | 0 | 0 | |
| Precision (%) | 68 | 25 | 100 | 0 | 0 | 0 | |
| RMSE | 12.86 | 92.21 | 0.57 | — | — | 20.90 | |
| LJL | TN | 331 | 2669 | 365 | 34 | 837 | 544 |
| CN | 215 | 1194 | 241 | 7 | 478 | 377 | |
| Precision (%) | 65.0 | 44.7 | 66.0 | 20.6 | 57.1 | 69.3 | |
| RMSE | 2.48 | 0.97 | 1.30 | 98.75 | 1.30 | 6.15 | |
| Proposed | TN | 14 | 190 | 320 | 19 | 21 | 30 |
| CN | 14 | 190 | 320 | 19 | 20 | 29 | |
| Precision (%) | 100 | 100 | 100 | 100 | 95.2 | 99.2 | |
| RMSE | 0.80 | 0.60 | 0.45 | 0.69 | 1.17 | 0.99 |
| Initial Matches | RANSAC | LIL | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IN | IC | IF | CN | FN | DF | DC | RMSE | Time | CN | FN | DF | DC | RMSE | Time | |
| 1 | 105 | 15 | 90 | 10 | 8 | 82 | 7 | 16.34 | 0.32 | 14 | 0 | 90 | 1 | 0.80 | 0.35 |
| 2 | 643 | 263 | 380 | 260 | 110 | 270 | 3 | 2.89 | 0.08 | 190 | 0 | 380 | 73 | 0.60 | 8.74 |
| 3 | 594 | 342 | 252 | 338 | 89 | 163 | 4 | 2.32 | 0.02 | 320 | 0 | 252 | 22 | 0.45 | 6.88 |
| 4 | 167 | 19 | 148 | 18 | 21 | 127 | 1 | 13.18 | 0.34 | 19 | 0 | 148 | 0 | 0.69 | 0.89 |
| 5 | 310 | 24 | 286 | 3 | 17 | 269 | 21 | — | 0.39 | 20 | 1 | 285 | 4 | 1.17 | 2.14 |
| 6 | 142 | 30 | 112 | 28 | 22 | 90 | 2 | 35.37 | 0.33 | 29 | 1 | 111 | 1 | 0.99 | 0.62 |
| [0, 1) | [1, 2) | [2, 3) | |
|---|---|---|---|
| RANSAC | 65 | 105 | 90 |
| LIL | 65 | 84 | 41 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Jiang, J. Registration Algorithm Based on Line-Intersection-Line for Satellite Remote Sensing Images of Urban Areas. Remote Sens. 2019, 11, 1400. https://doi.org/10.3390/rs11121400
Liu S, Jiang J. Registration Algorithm Based on Line-Intersection-Line for Satellite Remote Sensing Images of Urban Areas. Remote Sensing. 2019; 11(12):1400. https://doi.org/10.3390/rs11121400
Chicago/Turabian StyleLiu, Siying, and Jie Jiang. 2019. "Registration Algorithm Based on Line-Intersection-Line for Satellite Remote Sensing Images of Urban Areas" Remote Sensing 11, no. 12: 1400. https://doi.org/10.3390/rs11121400
APA StyleLiu, S., & Jiang, J. (2019). Registration Algorithm Based on Line-Intersection-Line for Satellite Remote Sensing Images of Urban Areas. Remote Sensing, 11(12), 1400. https://doi.org/10.3390/rs11121400