Next Article in Journal
Improved Spring Vegetation Phenology Calculation Method Using a Coupled Model and Anomalous Point Detection
Next Article in Special Issue
Advances in the Derivation of Northeast Siberian Forest Metrics Using High-Resolution UAV-Based Photogrammetric Point Clouds
Previous Article in Journal
Differential Inter-System Biases Estimation and Initial Assessment of Instantaneous Tightly Combined RTK with BDS-3, GPS, and Galileo
Previous Article in Special Issue
Tree Height Estimation of Forest Plantation in Mountainous Terrain from Bare-Earth Points Using a DoG-Coupled Radial Basis Function Neural Network
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 11
Issue 12
10.3390/rs11121431
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Comparison of Two Tree Detection Methods for Estimation of Forest Stand and Ecological Variables from Airborne LiDAR Data in Central European Forests

by
Ivan Sačkov
1,2,*,
Ladislav Kulla
2 and
Tomáš Bucha
2
1
Department of Ecology and Natural Resource Management, Norwegian University of Life Sciences, P.O. Box 5003, NO-1432 Ås, Norway
2
Department of Forest Policy, Economics and Forest Management, National Forest Centre-Forest Research Institute Zvolen, T.G. Masaryka 22, 960 01 Zvolen, Slovak Republic
*
Author to whom correspondence should be addressed.
Remote Sens. 2019, 11(12), 1431; https://doi.org/10.3390/rs11121431
Submission received: 17 May 2019 / Revised: 30 May 2019 / Accepted: 31 May 2019 / Published: 16 June 2019
(This article belongs to the Special Issue 3D Point Clouds in Forests)
Browse Figures
Versions Notes

Abstract

:
Estimation of biophysical variables based on airborne laser scanning (ALS) data using tree detection methods concentrates mainly on delineation of single trees and extraction of their attributes. This study provides new insight regarding the potential and limits of two detection methods and underlines some key aspects regarding the choice of the more appropriate alternative. First, we applied the multisource-based method implemented in reFLex software (National Forest Centre, Slovakia), which uses the information contained in the point cloud and a priori information. Second, we applied the raster-based method implemented in OPALS software (Vienna University of Technology, Austria), which extracts information from several ALS-derived height models. A comparative study was conducted for a part of the university forest in Zvolen (Slovakia, Central Europe). ALS-estimated variables of both methods were compared (1) to the ground reference data within four heterogonous stands with an area size of 7.5 ha as well as (2) to each other within a comprehensive forest unit with an area size of 62 ha. We concluded that both methods can be used to evaluate forest stand and ecological variables. The overall performance of both methods achieved a matching rate within the interval of 52%–64%. The raster-based method provided faster and slightly more accurate estimate of most variables, while the total volume was more precisely estimated using the multisource-based method. Specifically, the relative root mean square errors did not exceed 7.2% for mean height, 8.6% for mean diameter, 21.4% for total volume, 29.0% for stand density index, and 7.2% for Shannon’s diversity index. Both methods provided estimations with differences that were statistically significant, relative to the ground data as well as to each other (p < 0.05).

Graphical Abstract

1. Introduction

Forest ecosystems are an important base for renewable raw materials and natural resources. These ecosystems are, however, exposed to permanent disturbances caused by human actions and by biological or climatic agents (deforestation, forest fires, bark beetles outbreaks, droughts, etc.). Precise and up-to-date information about the state of forests and their changes is, therefore, very important for sustainable forest management, natural resource protection, and for forest science.
Remote sensing (RS) technologies represent an effective way to acquire relevant information about forest ecosystems. Specifically, airborne laser scanning (ALS), also known as airborne light detection and ranging (airborne LiDAR), as an active RS technology, provides an opportunity to complement ground-based inventories. This is primarily because these systems can penetrate a laser beam through even dense and multi-layered forest canopies to the ground, and they can be used to directly estimate a spatially explicit three-dimensional canopy structure with submeter accuracy in real time [1,2].
This study focused on estimation of forest stand and ecological variables based on ALS data using individual tree detection approach (ITD). ITD-based techniques usually involve a sequence of tree detection, feature extraction, and estimation of tree attributes [3]. In general, tree tops/crowns and tree heights are extracted directly from ALS data or ALS-based derivatives, whereas other tree and stand variables are inferred indirectly [4]. Regarding tree detection and tree height extraction, there are three dominant groups of methods in relation to input data format: (1) Raster-based, (2) point-based, and (3) multisource-based. The review performed by Zhen et al. [5] showed that the raster-based methods are preferred. These methods use different types of digital models as input and, therefore, are relatively easy to use (i.e., digital terrain model (DTM), digital surface model (DSM), and canopy height model (CHM)). On the other hand, these methods require some interpolation or smoothing procedures, and they also largely reduce information regarding the understory [6]. The original point cloud is used less frequently [5]. These point-based methods are usually computationally demanding, but most information from the whole three-dimensional structure of the source is taken into account within feature extraction. The main representatives of this method are k-means clustering techniques [7,8,9] and voxel-based segmentations of single trees [10,11,12]. The multisource-based methods combine different raster layers and/or point-clouds and/or a priori information (e.g., allometric rules). As an example, Reitberger et al. [13] reported a method that retrieves points associated with crown segments, which are extracted from the CHM. The region-growing algorithm by Tiede and Hoffmann [14] regulates the tree detection process based on the minimal height and maximal permissible width of a tree crown. Ene et al. [15] proposed to use the area-based estimate of stem numbers for optimizing the CHM resolution and filter size. Swetnam and Falk [16] included a rule based on the expected canopy radius in the treetop detection algorithm that prevents branches of a single tree crown to be classified as the local maxima. Diameters to breast height (DBH) and volumes of detected trees are mostly estimated using allometric models, geometrically weighted regression methods, or various nonparametric approaches [17,18]. Regardless of the detection techniques, however, stand variables that are directly linked to the number of detected trees are often underestimated due to problems in detecting suppressed and understory trees (e.g., growing stock). To overcome this problem, semi-ITD approaches and several techniques for modeling understory trees have been proposed [19,20,21,22,23].
Although a number of studies for ITD-based estimation of forest ecosystems variables have been reported, they mostly focused only on a few forest inventory variables within one study. Moreover, relatively few studies have dealt with estimation of ecological variables and with the benchmark of different groups of methods for these purposes. The overall objective of this study was, therefore, to use and compare two totally different tree detection methods to estimate few selected forests stand as well as ecological variables in heterogeneous forests located in Central Europe. We selected the multisource-based method implemented in reFLex software and the raster-based method implemented in OPALS software for comparison because (1) “reFLex” method uses original point cloud and allometric rules, while “OPALS” method uses only ALS-derived digital models, (2) “reFLex” method has not yet been broadly tested, while “OPALS” method achieved one of the best performance within international benchmarks [24], and (3) “reFLex” method is developed by corresponding authors for common application in forest inventories at the national level. We focused on five characteristics, namely mean height, mean diameter, total volume, stand density index, and Shannon’s diversity index of the tree species. The first three characteristics have a particular importance in forest management and represent the main forest stand variables. The last two characteristics are especially important for ecological applications and describe a measure of the stocking and tree species diversity in a given forest.

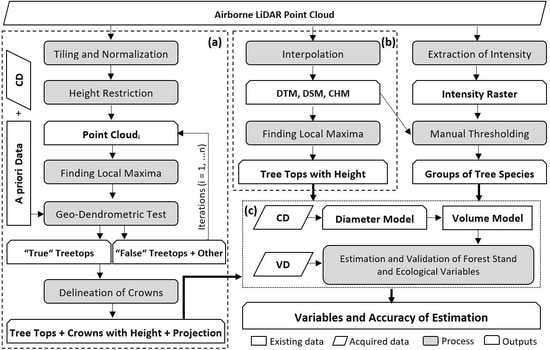
2. Materials and Methods

The study area is located in central Slovakia and represents a part of the University Forest Enterprise of the Technical University in Zvolen (48°37’N, 19°05´E). The main part of the area is situated in the mountain orographic unit of the Kremnické and Štiavnické Vrchy. The elevation reaches intervals of 250–1025 m above sea level and the dominating exposures are south, east, and south-west. The southern parts are characterized by thermophile species, while the north slopes and ridges have typical mountain species.
Discrete ALS data and two groups of field data were available for purpose of this study: (1) Ground calibration data for construction of DBHs models and (2) ground reference data for validation of both methods (Figure 1).

2.1. Estimation of Forest Stand Variables from Ground Reference Data

Ground reference data were collected during the leaf-on season in 2013 within four reference forest stands with different types of species mix (dominance of conifers, dominance of broadleaves, and a mix of conifers and broadleaves). Dominant species include European beech (Fagus sylvatica Linnaeus), Sessile oak (Quercus petraea Lieblein), European hornbeam (Carpinus betulus Linnaeus), European silver fir (Abies alba Miller), and Norway spruce (Picea abies Linnaeus). These stands covered approximately 7.5 ha, and their border was determined with GNSS measurements, resulting in a positional error of less than 1 m. A total of 2203 trees with DBH ≥ 7 cm and heights ≥ 5 m were measured for species, height, diameter, and vitality. A tree height threshold (5 m) was set with respect to conventional forest definitions by FAO FRA [25]. Tree height measurements were taken by the Vertex system and vertical accuracy was expected to be ±1.0 m. Measurements of DBH were performed with calipers at the millimeter scale. An overview of the ground reference data is presented in Table 1.
The quadratic mean diameter (dq) was calculated based on diameters at breast height (Equation (1)), and the quadratic mean height (hdq) was calculated using a regression height of the trees with dq as predictor.
d q   = ∑ i = 1 N D B H i 2 N ,
where N is number of trees, DBH is diameter at breast height in centimeters, and i is the indices for the i-th tree.
The total volume (V) calculation was obtained by summing up the tree data (v). The volumes of the measured trees were calculated based on models introduced by Petráš et al. [25]. The model predictors are tree height and diameter for the selected tree species (Equation (2)). The accuracy for these models reaches an average of 10% and empirical material includes 1886 broadleaved trees and 3588 coniferous trees from areas across Slovakia and Czechia.
v = f ( D B H , h ) ,
where DBH is the diameter at breast height in centimeters and h is tree height in meters.
Stand density indexes (SDI) were calculated based on the number of trees per hectare and the quadratic mean diameter (Equation (3)).
S D I = N P H × ( d q 25 ) 1.605 ,
where NPH is the number of trees per hectare and dq is the quadratic mean diameter in centimeters.
Shannon’s diversity indexes (H) were calculated based on the relative proportion of tree species to the total number of species (Equation (4)).
H = − ∑ l = 1 S p l ( l n p l ) ,
where S is number of tree species and pl is proportion of the l-th species to the total number of trees.

2.2. Estimation of Forest Stand Variables from ALS Data

ALS data acquisition was performed in September 2011 using a Riegl L-680i scanner. The study area was scanned from an altitude of 700 m with a 60° field of view, 320 kHz laser pulse repetition rate (PRR), and 122 Hz sampling rate (SR). The resulting vertical standard error was 0.047 m and the average density of point cloud reached 5.1 point/m2.
The estimation of forest stand and ecological variables from ALS data was carried out on a workstation with 8-core Intel(R) Xeon(R) CPU E5-2665 2.4 GHz processor and 32.0 GB RAM. The workflow for both methods is shown in Figure 2 and described in detail in following sections.

2.2.1. Individual Tree and Tree Height Detection

Regarding the multisource-based method, the treetops, tree crowns, and tree heights were detected using the reFLex algorithm (National Forest Centre, Zvolen, Slovakia). There, the initial procedures (1) divided the points into a three-dimensional regular mesh, (2) calculated the absolute height above the ground for each point, and (3) reduced the number of points in the input file by applying a minimum tree height threshold (5 m). These operations produced a point cloud that was further used in an iterative search for treetops and tree crowns by using a moving-window analysis. Since there is a reason to assume that a part of the local maxima identified in the previous operation may not be indicative of real treetops, an additional geo-dendrometric (GD) test was applied. The GD test is linked to a priori information and includes two steps: (1) Evaluation of height differences between the local maxima, and (2) evaluation of horizontal and vertical distances between the local maxima. In this way, false treetops situated in the crowns of other trees are removed. The final procedures were applied to delineate the tree crowns. After the treetop identification and crown delineation phases were completed, tree height was recorded and crown coverage was calculated. Finally, the outputs of all procedures were exported to point and polygon vector files in an ESRI shapefile format. All details of the algorithm are listed in the study of Sačkov et al. [26].
Regarding the raster-based method, the treetops and tree heights were detected using OPALS algorithm (Institute of Photogrammetry and Remote Sensing, Dept. of Geodesy and Geoinformation at the University of Technology in Vienna, Austria). The process of tree identification was carried out at input spatial resolutions of 1.5 m [27]. At first, the “cell module” was used for the derivation of models through accumulating the laser heights. Subsequently, two DSMs were created with a grid equal to the input spatial resolution. The first DSM was created using the interpolation method of moving planes with the quadrant selection mode. Hereby, a grid dataset was created representing the sigma of the grid post adjustment (i.e., the standard deviation of the unit weight observation). The second DSM was created by the aggregation of the maximum values for laser height. The final DSM was created by combining these two DSMs and the sigma raster layer using the “algebra module”. The DTM with a grid equal to the input spatial resolution was derived using the moving planes interpolation method with the quadrant selection mode. The CHM was created by subtracting the DTM from DSM. Statistical filtering was performed on the CHM using the “StatFilter module”. The shape of the kernel environment was a circle and the max value was set as a parameter (i.e., the cell with highest value inside the defined area). In this way, the local maxima were localized across the whole study area. Grids representing the CHM and local maxima were combined using the “algebra module”. The result was a grid representing the positions and heights of the individual trees. All details on the algorithms are listed in OPALS manuals [28].

2.2.2. Classification of Tree Species Groups

The classification was carried out for two general groups of tree species: (1) Broadleaves, and (2) conifers. These groups were classified based on combination of intensity raster and CHM with pixel size of 1.0 m. First, the range of spectral information in the form of the backscatter intensity of the laser signal for each group of species was identified through visual interpretation, and the intensity raster with pixels representing broadleaves, conifers, and ground was created. Second, pixels smaller than 5 m CHM height were removed from the intensity raster and, thus, the final intensity raster included only the broadleaved and coniferous group. Finally, one of the species groups was assigned to detected trees using zonal statistical functions.

2.2.3. Tree Diameter Derivation

The DBHs of the detected trees were derived based on nonlinear regression models through tree height as predictor. We found the exponential function to be most suitable for DBH derivation based on tree height (Table 2). The statistical significance of models was assessed using the F-test at a significance level of α = 0.05. Here, the empirical material included 1372 trees from nine calibration plots covering a total area of 3.3 ha (Figure 1). A prevailing terrain slopes, development stages, and tree species mixture occurring in the reference forest stands were represented in these plots [29].

2.2.4. Tree Volume Derivation

The volume for detected trees was derived based on the same models and equations as in the case of the ground data (Equation (2)).

2.2.5. Calculation of Forest Stand and Ecological Variables

With respect to selected criteria (Section 2.1), only ALS-detected trees higher than 5 m were used for the purposes of this study. The stand height and stand diameter were obtained as the average of the tree data. The total volume calculation was obtained by summing up the tree data. The stand density index and Shannon’s diversity index for detected trees were calculated based on the same models and equations as in the case of the ground data (Equations (3) and (4)).

2.3. Accuracy Assessment

2.3.1. Forest Stands Level

An accuracy assessment was carried out for the reference stands (7.5 ha). ALS-estimated stand variables using multisource-based and raster-based methods were compared to the ground reference data.
First, the following detection rates were assessed: (1) Extraction rate (ER), as the rate of all detected trees; (2) matching rate (MR), as the rate of detected trees that could be matched; (3) commission rate (CR), as the rate of detected trees that could not be matched; and (4) omission rate (OR), as the rate of reference trees that could not be matched.
Second, the overall accuracy for multisource-based and raster-based methods was assessed based on comparing ALS-estimated and ground-measured stand variables. The mean difference (e) was calculated as the average of individual differences and was used as an indicator of underestimation or overestimation. The random error component (se) was used to assess the dispersion of differences around the mean difference. The root mean square error (RMSE) was used to aggregate both the systematic and random error components. The resulting RMSE should indicate the range of total accuracy for the whole study area at the 68% confidence level. The relative e%, se%, and RMSE% were calculated as the ratios of their absolute values and the arithmetic average of the reference data. In addition, we used the Wilcoxon Test to assess the significance of differences (p < 0.05). This non-parametric test was selected primarily because a normal distribution of mean differences was not confirmed within the dataset (p < 0.05).
Third, we evaluated the effect of (1) detection rates and (2) selected stand parameters (in terms of tree species composition, mean height, mean diameter, and crown coverage, slope) on overall accuracy of ALS-estimations.

2.3.2. Forest Unit Level

An accuracy assessment was carried out for a comprehensive forest unit that was divided into a 10 × 10 m grid (62 ha; 6250 grid cells). ALS-estimated stand and ecological variables using multisource-based and raster-based methods were compared to each other within all grid cells.

3. Results

3.1. Forest Stands Level

The detection of individual trees and subsequent estimation of forest stand and ecological variables using the multisource-based method took 150 s (20.0 s ha−1), while the raster-based method lasted 102 s (13.6 s ha−1).
In Table 3, the detection results per method are summarized. The best matching rate was found within the forest stands where coniferous trees dominated. Specifically, the overall performance of both methods achieved the matching rate within the interval of 52%–64% and the omission rate ranged from 36% to 48%. In contrast, the incorrect detections with an average value of 9% and 36% was produced by multisource-based and raster-based method, respectively.
The overview of relative differences between ALS-estimated and ground-measured variables using multisource-based and raster-based method is presented in Table 4 and Table 5. The raster-based method provided slightly more accurate estimate of most variables, while the total volume was more precisely estimated using the multisource-based method. Here, the total volume of false positive trees was only 20.3 m3 ha−1 for multisource-based method, but up to 137.1 m3 ha−1 for the raster-based method. The compared methods provided outputs with differences that were statistically significant relative to the ground data as well as to each other (p < 0.05).
The effect of commission rate on accuracy of ALS-estimated variables was particularly pronounced in the case of the raster-based method in relation to the total volume and SDI. The ALS-estimated variables also showed sensitivity to selected stand parameters. The strong relationship (R2 > 0.7) was found between detection ratio and tree species mixture as well as between the ALS-estimated mean height, mean diameter, total volume, and ground-measured variables, such as number of trees per hectare, quadratic mean height and diameter, and volume per hectare.

3.2. Forest Unit Level

The detection of individual trees and subsequent estimation of forest stand and ecological variables using the multisource-based method took 1200 s (19.4 s ha−1), while the raster-based method lasted 780 s (12.6 s ha−1).
The individual difference between methods reached the values of 1.1 m for mean height, 1.5 cm for mean diameter, 1.2 m3 for mean volume, 151.7 units for mean stand density index, and 0.1 units for mean Shannon’s diversity index. Simultaneously, these differences were statistically significant (p < 0.05). In Table 6, the estimated variables per method are summarized. The maps of estimated variables for a comprehensive forest unit over grid cells (10 × 10 m) are displayed in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7.

4. Discussion

4.1. Mean Height

Our results confirmed the general statement that stand height is the most accurate forest inventory attribute within direct estimations based on the ALS data [30,31]. In this study, the mean error ranged from −3.4% to 9.6% and RMSE% did not exceed the level of 7.2%. A slightly higher accuracy was achieved by the raster-based method (RMSE% = 6.1%) and within reference stands with substantial or moderate dominance of coniferous trees (C and CB). The trend related to differences, and their over- or underestimations was similar for both methods. The accuracy of the ALS-estimated mean height decreased with increasing stand density and increased as all other stand parameters increased. However, terrain slope of 15° or more caused an underestimation of the mean height. This underestimation could also be because the point density was relatively low. For example, Andersen et al. [32] reported a density of 5 points/m2 as a minimum, and Takahashi et al. [33] recommended a density of at least 9 points/m2 in order to achieve a difference in height estimates lower than 1 m. Despite the relative low density of the point cloud, however, our results for both alternative methods were within the range of achievable accuracy (6%–33%) indicated by Kaartinen and Hyyppä [34].

4.2. Mean Diameter

The average accuracy of the one-parameter nonlinear regression models, which were used for DBH derivation, reached 19% in terms of standard error of estimates. Based on these models, we found that both alternative methods overestimated the mean diameter, but the difference between methods was minimal (0.8%). In detail, mean error reached value of 6.9 ± 6% for the multisource-based method and value of 6.1 ± 6% for the raster-based method. In both cases, the RMSE% was less than 9% and accuracy increased with increasing mean height. On the other hand, with increasing total volume and stem density, this accuracy decreased. Although the models used for DBH derivation in this study were relatively simple, the accuracy of mean diameter estimation was slightly higher than reported by other comparative studies [35,36]. These studies provided accuracies of 15%–23% in terms of RMSE%, and models for DBH derivation often included more variables than just tree height (e.g., crown area, crown height, crown volume).

4.3. Total Volume

The volume of trees usually is calculated using volume models or equations, where information about tree height and diameter is required. In this study, we used two-parameter volume equations with an average accuracy of 10%. Here, we found the most striking differences between total volumes calculated using compared methods. The multisource-based method underestimated total volume within all reference stands. Mean error varied from −19.1% to −9.3%, and RMSE% was 15.0%. The raster-based method, however, overestimated total volume within all reference stands. Mean error varied from 6.3% to 31.1%, and RMSE% was 21.4%. On the other hand, in both cases, higher accuracy was found within reference stands with majority of coniferous trees (C). The accuracy decreased with increasing stand density, but increased as all other stand parameters increased.
With respect to other studies (e.g., [37]), negative biases are achievable with higher probability and they are basically expected for the ITD approach; if some type of correction is not used and the fundamental requirement is also a low rate of commission error. Based on results from this study (Table 2) as well as previous research [24,27], however, the raster-based method provides relatively many false positive trees. In this context, results provided by the multisource-based method could be considered more relevant and, ultimately, more accurate if some type of correction is not used. Other studies reported the accuracy ranged between 20%–43% [38] and different structures of volume models there were used. As an example, Næsset [39] used a percentile of pulse laser heights and canopy density for tree volume calculation. An even more complicated volume model was proposed by Tesfamichael et al. [40] that contained up to four predictors for tree volume calculation (i.e., ALS-derived height variables, stems per hectare, stand age, and the level of association between estimated and observed volume).

4.4. Stand Density Index

The SDI defines tree stocking level and, in a broad sense, describes wildlife thermal and hiding cover [41]. A relative measure of stand density provides a relationship between the number of trees per hectare and their quadratic mean diameter. In this study, the multisource-based method underestimated the SDI within all reference stands. The range of mean error was relatively small, from -24.0% to -32.6%, and the RMSE% was 29.0%. The raster-based method tended to overestimate SDI, with the exception of coniferous stand (C). This method estimated the SDI with a wider range of mean error, from -11.0% to 16.0%, and the RMSE% was 14.7%.
With regards to the SDI formula, the crucial point for density prediction represents the performance of tree detection. Here, the extraction algorithm and point density or grid resolution is the main factor affecting the accuracy of tree detection [32]. A very fine grid resolution increases the potential for false positives (commission rate), while a too-coarse resolution or low scanning density leads to an increased number of undetected trees (omission rate). Vauhkonen et al. [42] stated that the accuracy of tree detection in Scandinavia and Central Europe forests should be around 70%. Regarding algorithms used in this study, the accuracy of tree detection is found within the interval of 52%–84% according to the results from this study (Table 2) and previous research for the same study area [26,27]. However, the commission rate of the raster-based method may exceed 45%, while the commission rate of multisource-based method is usually within 8%. This is because the algorithm used in the multisource-based method includes an iterative process for the elimination of false treetops. All this ultimately causes significant differences between alternative methods, especially for cumulative stand variables (e.g., tree stocking).

4.5. Shannon’s Diversity Index

The H is a mathematical measure of tree species diversity and provides important information about the rarity and commonness of species in given forests. Specifically, it is the relative proportion of tree species to the total number of species, where H = 1 means complete evenness of tree species across the study area. The estimation of tree species diversity using ALS data has proven to be a difficult task because of the lack of spectral information [43]. Species-specific estimations are, therefore, mostly realized by combining ALS data and aerial photography. The correct spatial adjustment of the information derived from diverse sensors, however, is required in these cases [44].
In this context, our study applied only spectral information in the form of backscatter intensity of the ALS data for tree species classification and for subsequent tree species diversity estimation. Both algorithms overestimated the H value in coniferous and mixed forest (CB and BC). In the case of reference stands with broadleaved forest (B), the H values were underestimated. Overall, the differences between methods did not exceed 3.5% at both levels. A similar data source was chosen by Ørka et al. [45] or by Korpela et al. [46]. These studies were focused on the classification of coniferous and broadleaved trees and they reported an overall accuracy in the range of 33%–88%. Dalponte et al. [47] focused directly on the prediction of Shannon’s diversity index. The mean absolute deviation reached value of 9.6% when an area-based approach and a Leica ALS70 scanner was used.

5. Conclusions

This study demonstrated that forest stand and ecological variables can be estimated with sufficient accuracy using tree detection methods from both original ALS point clouds and ALS-derived digital models.
As expected, the raster-based method was less time consuming than the multisource-based method. The difference in time consumption was, however, only 6 s per hectare, and the algorithm of multisource-based method additionally included an iterative verification of detected trees. In this context, the estimation of cumulative variables, such as total volume and SDI, should be less affected by false positive trees when using the multisource-based method. On the other hand, the raster-based method provided slightly more accurate estimations for all other stand and ecological variables. The overall accuracy of most variables increased with increasing the proportion of coniferous trees, mean height, and diameter, but decreased with increasing stand density. The compared methods provided estimations with differences that were statistically significant relative to the ground data as well as to each other.
Future research should include gradual testing of the methods in different forest conditions to assess their applicability to forest inventories practice. Furthermore, development of more precise models for DBH derivation, and testing of enhanced methods for tree species classification will be needed in the future.

Author Contributions

I.S. was involved in the whole study (i.e., conceptualization, methodology, reFLex software development and application, validation, investigation, ground reference data acquisition, writing/editing). L.K. and T.B. provided the theoretical background and supervision. All co-authors improved the article at various stages of the reviewing and writing process.

Funding

This research was supported by the Slovak Research and Development Agency in the framework of the project “Innovations in the forest inventories based on progressive technologies of remote sensing” (APVV-15-0393).

Acknowledgments

Ivan Sačkov acknowledges the receipt of a fellowship from the OECD Co-operative Research Programme: Biological Resource Management for Sustainable Agricultural Systems in 2019. Special thanks go to Gobakken for supervising. Additional thanks go to Smreček for application of OPALS software.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
GNSSGlobal Navigation Satellite System
IUFROInternational Union of Forest Research Organizations
FAOFood and Agriculture Organization of the United Nations References
ESRI shpEnvironmental Systems Research Institute Shapefile

References

  1. Véga, C.; Renaud, J.; Durrieu, S.; Bouvier, M. On the interest of penetration depth, canopy area and volume metrics to improve Lidar-based models of forest parameters. Remote Sens. Environ. 2016, 175, 32–42. [Google Scholar] [CrossRef]
  2. Zhang, Z.; Cao, L.; She, G. Estimating Forest Structural Parameters Using Canopy Metrics Derived from Airborne LiDAR Data in Subtropical Forests. Remote Sens. 2017, 9, 940. [Google Scholar] [CrossRef]
  3. Vauhkonen, J.; Maltamo, M.; McRoberts, R.E.; Næsset, E. Introduction to forestry applications of airborne laser scanning. In Forestry Application of Airborne Laser Scanning: Concept and Case Studies; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2014; pp. 1–16. [Google Scholar]
  4. Tuominen, S.; Pitkänen, J.; Balazs, A.; Korhonen, K.T.; Hyvönen, P.; Muinonen, E. NFI plots as complementary reference data in forest inventory based on airborne laser scanning and aerial photography in Finland. Silva Fenn. 2014, 48. [Google Scholar] [CrossRef] [Green Version]
  5. Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in Automatic Individual Tree Crown Detection and Delineation—Evolution of LiDAR Data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef]
  6. Lee, A.C.; Lucas, R.M. A LiDAR-derived canopy density model for tree stem and crown mapping in Australian forests. Remote Sens. Environ. 2007, 111, 493–518. [Google Scholar] [CrossRef]
  7. Morsdorf, F.; Meiera, E.; Kötza, B.; Ittena, K.I.; Dobbertinc, M.; Allgöwer, B. LiDAR-based geometric reconstruction of boreal type forest stands at single tree level for forest and wildland fire management. Remote Sens. Environ. 2004, 92, 353–362. [Google Scholar] [CrossRef]
  8. Gupta, S.; Weinacker, H.; Koch, B. Comparative analysis of clustering-based approaches for 3-D single tree detection using airborne fullwave LiDAR data. Remote Sens. 2010, 2, 968–989. [Google Scholar] [CrossRef]
  9. Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the LiDAR point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar]
  10. Popescu, S.C.; Zhao, K. A voxel-based LiDAR method for estimating crown base height for deciduous and pine trees. Remote Sens. Environ. 2008, 112, 767–781. [Google Scholar] [CrossRef]
  11. Wu, B.; Yu, B.; Yue, W.; Shu, S.; Tan, W.; Hu, C.; Huang, Y.; Wu, J.; Liu, H. A voxel-based method for automated identification and morphological parameters estimation of individual street trees from mobile laser scanning data. Remote Sens. 2013, 5, 581–611. [Google Scholar] [CrossRef]
  12. Amiria, N.; Polewskic, P.; Heurich, M.; Krzystek, P.; Skidmore, A.K. Adaptive stopping criterion for top-down segmentation of ALS point clouds in temperate coniferous forests. ISPRS J. Photogramm. Remote Sens. 2018, 141, 265–274. [Google Scholar]
  13. Reitberger, J.; Schnörr, C.; Krzystek, P.; Stilla, U. 3D Segmentation of single trees exploiting full waveform LiDAR data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 561–574. [Google Scholar]
  14. Tiede, D.; Hoffmann, C. Process oriented object-based algorithms for single tree detection using laser scanning data. In Proceedings of the Workshop on 3D Remote Sensing in Forestry, Vienna, Austria, 14–15 February 2006; p. 5. [Google Scholar]
  15. Ene, L.; Næsset, E.; Gobakken, T. Single tree in heterogeneous boreal forests using airborne laser scanning and area-based stem number estimates. Int. J. Remote Sens. 2012, 33, 5171–5193. [Google Scholar] [CrossRef]
  16. Swetnam, T.L.; Falk, D.A. Application of metabolic scaling theory to reduce error in local maxima tree segmentation from aerial LiDAR. For. Ecol. Manag. 2014, 323, 158–167. [Google Scholar] [CrossRef]
  17. Salas, C.; Ene, L.; Gregoire, T.G.; Næsset, E.; Gobakken, T. Modelling tree diameter from airborne laser scanning derived variables: A comparison of spatial statistics models. Remote Sens. Environ. 2010, 114, 1277–1285. [Google Scholar] [CrossRef]
  18. Packalén, P.; Maltamo, M. The estimation of species-specific diameter distribution using airborne laser scanning and aerial photographs. Can. J. For. Res. 2008, 38, 1750–1760. [Google Scholar] [CrossRef]
  19. Flewelling, J.W. Probability models for individually segmented tree crown images in a sampling context. In Proceedings of the SilviLaser 2008 8th International Conference on LiDAR Applications in Forest Assessment and Inventory, Heriot-Watt University, Edinburgh, UK, 17–19 September 2008; pp. 284–294. [Google Scholar]
  20. Breidenbach, J.; Næsset, E.; Lien, V.; Gobakken, T.; Solberg, S. Prediction of species specific forest inventory attributes using a nonparametric semi-individual tree crown approach based on fused airborne laser scanning and multispectral data. Remote Sens. Environ. 2010, 114, 911–924. [Google Scholar] [CrossRef]
  21. Lahivaara, T.; Seppanen, A.; Kaipio, J.P.; Vauhkonen, J.; Korhonen, L.; Tokola, T.; Maltamo, M. Bayesian approach to tree detection based on airborne laser scanning data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2690–2699. [Google Scholar] [CrossRef]
  22. Melville, G.; Stone, C.; Turner, R. Application of LiDAR data to maximise the efficiency of inventory plots in softwood plantations. N. Z. J. For. Sci. 2015, 45, 16. [Google Scholar] [CrossRef]
  23. Kansanen, K.; Vauhkonen, J.; Lahivaara, T.; Mehtatalo, L. Stand density estimators based on individual tree detection and stochastic geometry. Can. J. For. Res. 2016, 46, 1359–1366. [Google Scholar] [CrossRef] [Green Version]
  24. Eysn, L.; Hollaus, M.; Lindberg, E.; Berger, F.; Monnet, J.M.; Dalponte, M.; Kobal, M.; Pellegrini, M.; Lingua, E.; Mongus, D.; Pfeifer, N. A benchmark of LiDAR-based single tree detection methods using heterogeneous forest data from the Alpine space. Forests 2015, 6, 1721–1747. [Google Scholar] [CrossRef]
  25. Petráš, R.; Pajtík, J. Sustava cesko-slovenskych objemovych tabuliek drevin. Lesnicky casopis. 1991, 37, 49–56. (In Slovak) [Google Scholar]
  26. Sackov, I.; Hlásny, T.; Bucha, T.; Juriš, M. Integration of tree allometry rules to treetops detection and tree crowns delineation using airborne lidar data. IForest 2017, 10, 459–467. [Google Scholar] [CrossRef]
  27. Smreček, R.; Michnová, Z.; Sačkov, I.; Danihelová, Z.; Levická, M.; Tuček, J. Determining basic forest stand characteristics using airborne laser scanning in mixed forest stands of Central Europe. IForest 2018, 11, 181–188. [Google Scholar] [CrossRef] [Green Version]
  28. OPALS Manual. Orientation and processing of airborne laser scanning data: User documentation. Available online: http://geo. tuwien.ac.at/opals/html/index.html (accessed on 5 November 2018).
  29. Šmelko, Š.; Šebeň, V.; Bošeľa, M.; Sačkov, I.; Kulla, L. New Variants of Methods for Multi-Purpose Inventory and Monitoring of Forest Ecosystems Using Progressive Technologies; NLC-LVÚ Zvolen: Zvolen, Slovakia, 2014; p. 368. ISBN 978-80-8093-193-3. (In Slovak) [Google Scholar]
  30. Akkay, A.E.; Oguz, H.; Karas, I.R.; Aruga, K. Using LiDAR technology in forestry activities. Environ. Monit. Assess. 2009, 151, 117–125. [Google Scholar] [CrossRef] [PubMed]
  31. Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
  32. Andersen, H.E.; Reutebuch, S.E.; McGaughey, R.J. A rigorous assessment of tree height measurements obtained using airborne lidar and conventional field methods. Can. J. Remote Sens. 2006, 32, 355–366. [Google Scholar] [CrossRef]
  33. Takahashi, T.; Yamamoto, K.; Senda, Y.; Tsuzuku, M. Estimating individual-tree heights of sugi (Cryptomeria japonica D. Don) plantations in mountainous areas using small-footprint airborne LiDAR. J. For. Res. 2005, 10, 135–142. [Google Scholar] [CrossRef]
  34. Kaartinen, H.; Hyyppä, J. Tree extraction-Report of EuroSDR project. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=2ahUKEwi-hPOa6MfiAhXMyYsBHaRMD80QFjAAegQIAxAC&url=http%3A%2F%2Fbono.hostireland.com%2F~eurosdr%2Fpublications%2F53.pdf&usg=AOvVaw3iEPzkFdw06CbOp6niCnOx (accessed on 5 November 2018).
  35. Yu, X.; Hyyppä, J.; Vastaranta, M.; Holopainen, M. Predicting individual tree attributes from airborne laser point clouds based on random forest technique. ISPRS J. Photogramm. Remote Sens. 2011, 66, 28–37. [Google Scholar]
  36. Wu, J.; Yao, W.; Choi, S.; Park, T.; Myneni, R.B. A comparative study of predicting DBH and stem volume of individual trees in a temperate forest using airborne waveform LiDAR. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2267–2271. [Google Scholar] [CrossRef]
  37. Kandare, K.; Dalponte, M.; Ørka, H.O.; Frizzeria, L.; Næsset, E. Prediction of Species-Specific Volume Using Different Inventory Approaches by Fusing Airborne Laser Scanning and Hyperspectral Data. Remote Sens. 2017, 9, 400. [Google Scholar] [CrossRef]
  38. Peuhkurinen, J.; Mehtätalo, L.; Maltamo, M. Comparing individual tree detection and the area-based statistical approach for the retrieval of forest stand characteristics using airborne laser scanning in Scots pine stands. Can. J. For. Res. 2011, 41, 583–598. [Google Scholar] [CrossRef]
  39. Næsset, E. Practical large-scale forest stand inventory using a small-footprint airborne scanning laser. Scand. J. For. Res. 2004, 19, 164–179. [Google Scholar]
  40. Tesfamichael, S.G.; Aardt, J.A.N.; Ahmed, F. Estimating plot-level tree height and volume of Eucalyptus grandis plantations using small-footprint, discrete return LiDAR data. Prog. Phys. Geogr. 2010, 34, 515–540. [Google Scholar] [CrossRef]
  41. Moore, M.M.; Deiter, D.A. Stand Density Index as a Predictor of Forage Production in Northern Arizona Pine Forests. J. Range Manag. 1992, 45, 267–271. [Google Scholar] [CrossRef]
  42. Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkänen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M.; Lien, V.; Packalén, P.; Gobakken, T.; Koch, B.; Næsset, E.; Tokola, T.; Maltamo, M. Comparative testing of single-tree detection algorithms under different types of forest. Forestry 2012, 85, 27–40. [Google Scholar] [CrossRef]
  43. Yu, X.; Hyyppä, J.; Litkey, P.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Single-Sensor Solution to Tree Species Classification Using Multispectral Airborne Laser Scanning. Remote Sens. 2017, 9, 108. [Google Scholar] [CrossRef]
  44. Ballanti, L.; Blesius, L.; Hines, E.; Kruse, B. Tree Species Classification Using Hyperspectral Imagery: A Comparison of Two Classifiers. Remote Sens. 2016, 8, 445. [Google Scholar] [CrossRef]
  45. Ørka, H.O.; Næsset, E.; Bollandsås, O.M. Classifying species of individual trees by intensity and structure features derived from airborne laser scanner data. Remote Sens. Environ. 2009, 113, 1163–1174. [Google Scholar] [CrossRef]
  46. Korpela, I.; Ørka, H.O.; Maltamo, M.; Tokola, T. Tree species classification using airborne LiDAR-effects of stand and tree parameters, downsizing of training set, intensity normalization and sensor type. Silva Fenn. 2010, 44, 319–339. [Google Scholar] [CrossRef]
  47. Dalponte, M.; Ene, L.T.; Gobakken, T.; Næsset, E.; Gianelle, D. Predicting Selected Forest Stand Characteristics with Multispectral ALS Data. Remote Sens. 2018, 10, 586. [Google Scholar] [CrossRef]
Remotesensing 11 01431 g001 550
Figure 1. Location of the study area with position of nine calibration plots (black points) and four reference stands (Blue polygon: Dominance of conifers; purple and orange polygon: Mix of conifers and broadleaves; red polygon: Dominance of broadleaves).
Figure 1. Location of the study area with position of nine calibration plots (black points) and four reference stands (Blue polygon: Dominance of conifers; purple and orange polygon: Mix of conifers and broadleaves; red polygon: Dominance of broadleaves).
Remotesensing 11 01431 g001
Remotesensing 11 01431 g002 550
Figure 2. Flowchart of (a) multisource-based method and (b) raster-based method within the (c) estimation of forest stand and ecological variables. Note: CD: Calibration data; VD: Validation data; DTM, DSM: Digital terrain and surface model; CHM: Canopy height model.
Figure 2. Flowchart of (a) multisource-based method and (b) raster-based method within the (c) estimation of forest stand and ecological variables. Note: CD: Calibration data; VD: Validation data; DTM, DSM: Digital terrain and surface model; CHM: Canopy height model.
Remotesensing 11 01431 g002
Remotesensing 11 01431 g003 550
Figure 3. Maps of mean height over grid cell (10 × 10 m): (a) Multisource-based method and (b) raster-based method.
Figure 3. Maps of mean height over grid cell (10 × 10 m): (a) Multisource-based method and (b) raster-based method.
Remotesensing 11 01431 g003
Remotesensing 11 01431 g004 550
Figure 4. Maps of mean diameter over grid cell (10 × 10 m): (a) Multisource-based method and (b) raster-based method.
Figure 4. Maps of mean diameter over grid cell (10 × 10 m): (a) Multisource-based method and (b) raster-based method.
Remotesensing 11 01431 g004
Remotesensing 11 01431 g005 550
Figure 5. Maps of total volume over grid cell (10 × 10 m): (a) Multisource-based method and (b) raster-based method.
Figure 5. Maps of total volume over grid cell (10 × 10 m): (a) Multisource-based method and (b) raster-based method.
Remotesensing 11 01431 g005
Remotesensing 11 01431 g006 550
Figure 6. Maps of stand density index over grid cell (10 × 10 m): (a) Multisource-based method and (b) raster-based method.
Figure 6. Maps of stand density index over grid cell (10 × 10 m): (a) Multisource-based method and (b) raster-based method.
Remotesensing 11 01431 g006
Remotesensing 11 01431 g007 550
Figure 7. Maps of Shannon’s diversity index over grid cell (10 × 10 m): (a) Multisource-based method and (b) Raster-based method.
Figure 7. Maps of Shannon’s diversity index over grid cell (10 × 10 m): (a) Multisource-based method and (b) Raster-based method.
Remotesensing 11 01431 g007
Table
Table 1. Forest stand characteristics across reference stands.
Table 1. Forest stand characteristics across reference stands.
StandSR (%)A (ha)S (°)NPHhdq (m)dq (cm)VPH (m3)SDIH
C≥701.6416.5224133.7043.01520.77575.40.69
CB≈ 60/401.905.6219927.3135.76229.89353.30.64
BC≈ 60/402.704.5636624.5930.69292.95508.10.60
B≥\701.8510.7236425.2031.73337.97533.40.55
Note: C: Coniferous stand; CB: Con./Broad stand; BC: Broad./Con. stand; B: Broadleaved stand; SR (%): Ratio of tree species group in percent; A (ha): Area in hectare; S (°): Mean slope in degrees; NPH: Number of trees per hectare; hdq (m): Quadratic mean height in meters; dq (cm): Quadratic mean diameter in centimeters; VPH (m3): Total volume per hectare in cubic meters; SDI: Stand density index; H: Shannon’s diversity index.
Table
Table 2. Regression models for diameters to breast height (DBH) derivation.
Table 2. Regression models for diameters to breast height (DBH) derivation.
Tree Species GroupModel FormsNRR2SEESEE%p-Level
BroadleavesDBH = 6.152 × exp(0.058 × h) + ε7690.850.726.218.9<0.001
ConifersDBH = 8.054 × exp(0.053 × h) + ε6030.880.787.319.1<0.001
Note: N: Number of trees; R: Correlation coefficient; R2: Coefficient of determination; SEE: Standard error of estimates in centimeters; SEE%: Relative standard error of estimates; p-level: Significance of regression (F-test); h: Tree height in meters.
Table
Table 3. Detection results of the multisource-based method and raster-based method.
Table 3. Detection results of the multisource-based method and raster-based method.
Reference StandsMulti.-Based MethodRaster-Based Method
ERMRCRORERMRCROR
C675894297643336
CB655784396564044
BC645684492583442
B6655114589523748
Average665794494583643
Note: C: Coniferous stand; CB: Con./Broad stand; BC: Broad./Con. stand; B: Broadleaved stand; ER: Extraction rate; MR: Matching rate; CR: Commission rate; OR: Omission rate.
Table
Table 4. Relative differences between ALS-estimated and ground-measured data using the multisource-based method.
Table 4. Relative differences between ALS-estimated and ground-measured data using the multisource-based method.
Stand and Ecological VariablesCCBBCBAll
ei%e%se%RMSE%
Mean height−4.31.29.19.23.16.57.2
Mean diameter6.7−0.610.911.86.95.78.6
Total volume−10.2−11.7−21.3−14.9−14.24.915.0
Stand density index−30.3−24.3−33.1−24.8−28.34.329.0
Shannon’s diversity index−1.23.97.8−10.10.47.77.2
Note: C: Coniferous stand; CB: Con./Broad stand; BC: Broad./Con. stand; B: Broadleaved stand; ei%: Relative individual difference; e%: Relative mean error; se%: Relative standard deviation of mean error; RMSE%: Relative root mean square error.
Table
Table 5. Relative differences between ALS-estimated and ground-measured data using the raster-based method.
Table 5. Relative differences between ALS-estimated and ground-measured data using the raster-based method.
Stand and Ecological VariablesCCBBCBAll
ei%e%se%RMSE%
Mean height−2.80.17.38.92.85.66.1
Mean diameter7.7−2.28.111.26.15.88.3
Total volume3.829.319.130.618.712.421.4
Stand density index−15.05.34.417.52.513.514.7
Shannon’s diversity index−4.81.71.1−8.6−2.55.05.3
Note: C: Coniferous stand; CB: Con./Broad stand; BC: Broad./Con. stand; B: Broadleaved stand; ei%: Relative individual difference; e%: Relative mean error; se%: Relative standard deviation of mean error; RMSE%: Relative root mean square error.
Table
Table 6. ALS-estimated variables using the multisource-based method and raster-based method at forest unit level.
Table 6. ALS-estimated variables using the multisource-based method and raster-based method at forest unit level.
MethodHeight (m)Diameter (cm)Volume (m3)SDIH
MeanSDMeanSDMeanSDMeanSDMeanSD
Multi-based25.78.934.113.22.92.6366.6246.60.70.2
Raster-based24.69.932.614.54.14.3518.3416.60.60.2
Note: SDI: Stand density index; H: Shannon’s diversity index; SD: Standard deviation.

Share and Cite

MDPI and ACS Style

Sačkov, I.; Kulla, L.; Bucha, T. A Comparison of Two Tree Detection Methods for Estimation of Forest Stand and Ecological Variables from Airborne LiDAR Data in Central European Forests. Remote Sens. 2019, 11, 1431. https://doi.org/10.3390/rs11121431

AMA Style

Sačkov I, Kulla L, Bucha T. A Comparison of Two Tree Detection Methods for Estimation of Forest Stand and Ecological Variables from Airborne LiDAR Data in Central European Forests. Remote Sensing. 2019; 11(12):1431. https://doi.org/10.3390/rs11121431

Chicago/Turabian Style

Sačkov, Ivan, Ladislav Kulla, and Tomáš Bucha. 2019. "A Comparison of Two Tree Detection Methods for Estimation of Forest Stand and Ecological Variables from Airborne LiDAR Data in Central European Forests" Remote Sensing 11, no. 12: 1431. https://doi.org/10.3390/rs11121431

APA Style

Sačkov, I., Kulla, L., & Bucha, T. (2019). A Comparison of Two Tree Detection Methods for Estimation of Forest Stand and Ecological Variables from Airborne LiDAR Data in Central European Forests. Remote Sensing, 11(12), 1431. https://doi.org/10.3390/rs11121431

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop