Derivation of Vegetation Optical Depth and Water Content in the Source Region of the Yellow River using the FY-3B Microwave Data
Abstract
:1. Introduction
2. Algorithm Motivation
2.1. Classical Retrieval Approach for VOD and VWC
2.2. Determination of Influence of Open Water Fraction
3. Study Area and Data Source
3.1. Study Area
3.2. Field Observation Data
3.3. Remote Sensing Data
4. Results and Discussion
4.1. Spatial Distribution of 16-Day Mean NDVI and MVI
4.2. Fractional Coverage of Open Waterbodies
4.3. VOD Retrievals
4.3.1. Spatial Variation of Retrieved VOD
4.3.2. Temporal Variation of Retrieved VOD
4.3.3. Correlations between Retrieved VOD and Vegetation Indexes
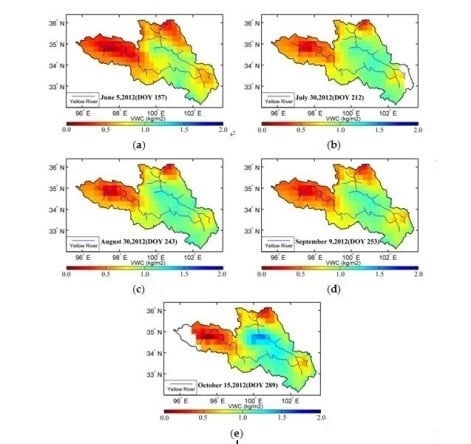
4.4. VWC Retrievals
4.5. Validation of VWC
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Colliander, A.; Cosh, M.H.; Misra, S.; Jackson, T.J.; Crow, W.T.; Chan, S.; Bindlish, R.; Chae, C.; Collins, C.H.; Yueh, S.H. Validation and scaling of soil moisture in a semi-arid environment: SMAP validation experiment 2015 (SMAPVEX15). Remote Sens. Environ. 2017, 196, 101–112. [Google Scholar] [CrossRef]
- Yi, L.; Zhang, W.C.; Li, X.Y. Assessing hydrological modelling driven by different precipitation datasets via the smap soil moisture product and gauged streamflow data. Remote Sens. 2018, 10, 1872. [Google Scholar] [CrossRef]
- Njoku, E.G.; Chan, S.K. Vegetation and surface roughness effects on AMSR-E land observations. Remote Sens. Environ. 2006, 100, 190–199. [Google Scholar] [CrossRef]
- Du, J.Y. A method to improve satellite soil moisture retrievals based on Fourier analysis. Geophysi. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Talebiesfandarani, S.; Zhao, T.J.; Shi, J.C.; Ferrazzoli, P.; Wigneron, J.P.; Zamani, M.; Pani, P. Microwave vegetation index from multi-angular observations and its application in vegetation properties retrieval: Theoretical modelling. Remote Sens. 2019, 11, 730. [Google Scholar] [CrossRef]
- Njoku, E.G.; Li, L. Retrieval of land surface parameters using passive microwave measurements at 6–18 GHz. IEEE Trans. Geosci. Remote Sens. 1999, 37, 79–93. [Google Scholar] [CrossRef]
- Kolassa, J.; Gentine, P.; Prigent, C.; Aires, F. Soil moisture retrieval from AMSR-E and ASCAT microwave observation synergy. Part 1: Satellite data analysis. Remote Sens. Environ. 2016, 173, 1–14. [Google Scholar] [CrossRef]
- Liu, Y.Y.; van Dijk, A.I.J.M.; de Jeu, R.A.M.; Canadell, J.G.; McCabe, M.F.; Evans, J.P.; Wang, G. Recent reversal in loss of global terrestrial biomass. Nat. Clim. Chang. 2015, 5, 470–474. [Google Scholar] [CrossRef]
- Jones, M.O.; Kimball, J.S.; Jones, L.A.; McDonald, K.C. Satellite passivemicrowave detection of North America start of season. Remote Sens. Environ. 2012, 123, 324–333. [Google Scholar] [CrossRef]
- Barichivich, J.; Briffa, K.R.; Myneni, R.B.; Osborn, T.J.; Melvin, T.M.; Ciais, P.; Piao, S.; Tucker, C. Large-scale variations in the vegetation growing season and annual cycle of atmospheric CO2 at high northern latitudes from 1950 to 2011. Glob. Chang. Biol. 2013, 19, 3167–3183. [Google Scholar] [CrossRef]
- Marle, M.V.; Werf, G.V.D.; Jeu, R.D.; Liu, Y. Annual South American forest loss estimates based on passive microwave remote sensing (1990–2010). Biogeosciences 2016, 13, 609–624. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
- Miralles, D.G.; Nieto, R.; McDowell, N.G.; Dorigo, W.A.; Verhoest, N.E.; Liu, Y.Y.; Teuling, A.J.; Dolman, A.J.; Good, S.P.; Gimeno, L. Contribution of water-limited ecoregions to their own supply of rainfall. Environ. Res. Lett. 2016, 11, 124007. [Google Scholar] [CrossRef]
- Jones, M.O.; Jones, L.A.; Kimball, J.S.; Mcdonald, K.C. Satellite passive microwave remote sensing for monitoring global land surface phenology. Remote Sens. Environ. 2011, 115, 1102–1114. [Google Scholar] [CrossRef]
- Meesters, A.; De, J.R.; Owe, M. Analytical derivation of the vegetation optical depth from the microwave polarization difference index. IEEE Geosci. Remote Sens. 2006, 2, 121–123. [Google Scholar] [CrossRef]
- Shi, J.C.; Jiang, L.M.; Zhang, L.X.; Chen, K.S.; Wigneron, J.P.; Chanzy, A.; Jackson, T.J. Physically based estimation of bare-surface soil moisture with the passive radiometers. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3145–3153. [Google Scholar] [CrossRef]
- Shi, J.C.; Jackson, T.J.; Tao, J.; Du, J.; Bindlish, R.; Lu, L.; Chen, K.S. Microwave vegetation indices for short vegetation covers from satellite passive microwave sensor AMSR-E. Remote Sens. Environ. 2008, 112, 4285–4300. [Google Scholar] [CrossRef]
- Njoku, E.G.; Ashcroft, P.; Chan, T.K.; Li, L. Global survey and statistics of radiofrequency interference in AMSR-E land observations. IEEE Trans. Geosci. Remote Sens. 2005, 43, 938–947. [Google Scholar] [CrossRef]
- Jones, L.A.; Ferguson, C.R.; Kimball, J.S.; Zhang, K.; Chan, S.T.K.; McDonald, K.C.; Njoku, E.G.; Wood, E.F. Satellite microwave remote sensing of daily land surface air temperature minima and maxima from AMSR-E. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 111–123. [Google Scholar] [CrossRef]
- Grant, J.P.; Wigneron, J.-P.; De Jeu, R.A.M.; Lawrence, H.; Mialon, A.; Richaume, P.; Al Bitar, A.; Drusch, M.; van Marle, M.J.E.; Kerr, Y. Comparison of SMOS and AMSR-E vegetation optical depth to four MODIS-based vegetation indices. Remote Sens. Environ. 2016, 172, 87–100. [Google Scholar] [CrossRef]
- Owe, M.; Jeu, R.D.; Walker, J. A methodology for surface soil moisture and vegetation opticaldepth retrieval using the microwave polarization difference index. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1643–1654. [Google Scholar] [CrossRef]
- Gao, H.; Wood, E.F.; Jackson, T.J.; Drusch, M.; Bindlish, R. Using TRMM/TMI to Retrieve Surface Soil Moisture over the Southern United States from 1998 to 2002. J. Hydrometer. 2006, 7, 815–818. [Google Scholar] [CrossRef]
- Oveisgharan, S.D.; Haddad, Z.; Turk, J.; Rodriguez, E.; Li, L. Soil moisture and vegetation water content retrieval using QuikSCAT data. Remote Sens. 2018, 10, 636. [Google Scholar] [CrossRef]
- Meyer, T.; Weihermüller, L.; Vereecken, H.; Jonard, F. Vegetation Optical Depth and Soil Moisture Retrieved from L-Band Radiometry over the Growth Cycle of a Winter Wheat. Remote Sens. 2018, 10, 1637. [Google Scholar] [CrossRef]
- Zheng, D.H.; Wang, X.; Velde, R.V.D.; Ferrazzoli, P.; Wen, J.; Wang, Z.L.; Schwank, M.; Colliander, A.; Bindlish, R.; Su, Z.B. Impact of surface roughness, vegetation opacity and soil permittivity on L-band microwave emission and soil moisture retrieval in the third pole environment. Remote Sens. Environ. 2018, 209, 633–647. [Google Scholar] [CrossRef]
- Jackson, T.J.; Schmugge, T.J. Vegetation effects on the microwave emission of soils. Remote Sens. Environ. 1991, 36, 203–212. [Google Scholar] [CrossRef]
- Liu, R.; Wen, J.; Wang, X.; Wang, Z.L. Validation of evapotranspiration and its long-term trends in the Yellow River source region. J. Water Clim. Chang. 2017, 8, 495–509. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing, Active and Passive; Artech House: Dedham, MA, USA, 1986; p. 2. [Google Scholar]
- Wang, J.R.; Choudhury, B.J. Remote sensing of soil moisture content over bare fields at 1.4 GHz frequency. J. Geophys. Res. 1981, 86, 5277–5282. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-Rayes, M.A. Microwave dielectric behavior of wet soil-Part II: Dielectric mixing models. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 35–46. [Google Scholar] [CrossRef]
- Holmes, T.R.H.; Drusch, M.; Wigneron, J.P.; RAMDe, J. A global simulation of microwave emission: Error structures based on output from ECMWF’s operational Integrated Forecast System. IEEE Trans. Geosci. Remote Sens. 2008, 46, 846–856. [Google Scholar] [CrossRef]
- Jackson, T.J.; O’Neill, P.E. Attenuation of soil microwave emissivity by corn and soybeans at 1.4 and 5 GHz. IEEE Trans. Geosci. Remote Sens. 1990, 28, 978–980. [Google Scholar] [CrossRef]
- Van De Griend, A.A.; Wigneron, J.P. The b-factor as a function of frequency and canopy type at H-polarization. IEEE Trans. Geosci. Remote Sens. 2004, 42, 786–794. [Google Scholar] [CrossRef]
- Jackson, T.J.; Le Vine, D.M.; Hsu, A.Y.; Oldak, A.; Starks, P.J.; Swift, C.T.; Ishan, J.D.; Haken, M. Soil moisture mapping at regional scales using microwave radiometry: The Southern Great Plains Hydrology Experiment. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2136–2151. [Google Scholar] [CrossRef]
- Jackson, T.J.; Hsu, A.Y.; O’Neill, P.E. Surface Soil Moisture Retrieval and Mapping Using High-Frequency Microwave Satellite Observations in the Southern Great Plains. J. Hydrometer. 2002, 3, 688–699. [Google Scholar] [CrossRef]
- English, S.J. The importance of accurate skin temperature in assimilating radiances from satellite sounding instruments. IEEE Trans. Geosci. Remote Sens. 2008, 46, 403–408. [Google Scholar] [CrossRef]
- Zheng, D.H.; Wang, X.; van der Velde, R.; Zeng, Y.; Wen, J.; Wang, Z.; Schwank, M.; Ferrazzoli, P.; Su, Z. L-Band Microwave Emission of Soil Freeze-Thaw Process in the Third Pole Environment. IEEE Trans. Geosci. Remote Sens. 2017, 99, 1–15. [Google Scholar] [CrossRef]
- Cui, Y.K.; Long, D.; Hong, Y.; Zeng, C.; Zhou, J.; Han, Z.Y.; Liu, R.H.; Wan, W. Validation and reconstruction of FY-3B/MWRI soil moisture using an artificial neural network based on reconstructed MODIS optical products over the Tibetan Plateau. J. Hydrometer. 2016, 543, 242–254. [Google Scholar] [CrossRef]
- Yang, J.T.; Jiang, L.M.; Shi, J.C.; Wu, S.L.; Sun, R.J.; Yang, H. Monitoring snow cover using Chinese meteorological satellite data over China. Remote Sens. Environ. 2014, 143, 192–203. [Google Scholar] [CrossRef]
- Paloscia, S.; Pampalonil, P. Microwave vegetation indexes for detecting biomass and water conditions of agricultural crops. Remote Sens. Environ. 1992, 40, 15–26. [Google Scholar] [CrossRef]
- Chen, S.Y.; Yu, H.; Feng, Q.S.; Liang, T.G. Dynamic monitoring of vegetation water content based on microwave remote sensing in Qinghai-Tibetan Plateau region from 2002 to 2010. Acta Prataculturae Sinica. 2013, 5, 1–10. [Google Scholar]
- Dente, L.; Vekerdy, Z.; Wen, J.; Su, Z. Maqu network for validation of satellite-derived soil moisture products. Int. J. Appl. Earth Obs. 2012, 17, 55–65. [Google Scholar] [CrossRef]














| Frequencies (GHz) | 10.65 | 18.7 | 23.8 | 36.5 | 89 |
|---|---|---|---|---|---|
| Polarization | V.H | V.H | V.H | V.H | V.H |
| Bandwidth (MHz) | 180 | 200 | 400 | 900 | 2 × 2300 |
| Calibration accuracy (K) | 1.0 | 2.0 | 2.0 | 2.0 | 2.0 |
| Spatial resolution (km × km) | 51 × 85 | 30 × 50 | 27 × 45 | 18 × 30 | 9 × 15 |
| Swath width (Km) | 1400 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Wen, J.; Wang, X.; Wang, Z.; Li, Z.; Xie, Y.; Zhu, L.; Li, D. Derivation of Vegetation Optical Depth and Water Content in the Source Region of the Yellow River using the FY-3B Microwave Data. Remote Sens. 2019, 11, 1536. https://doi.org/10.3390/rs11131536
Liu R, Wen J, Wang X, Wang Z, Li Z, Xie Y, Zhu L, Li D. Derivation of Vegetation Optical Depth and Water Content in the Source Region of the Yellow River using the FY-3B Microwave Data. Remote Sensing. 2019; 11(13):1536. https://doi.org/10.3390/rs11131536
Chicago/Turabian StyleLiu, Rong, Jun Wen, Xin Wang, Zuoliang Wang, Zhenchao Li, Yan Xie, Li Zhu, and Dongpeng Li. 2019. "Derivation of Vegetation Optical Depth and Water Content in the Source Region of the Yellow River using the FY-3B Microwave Data" Remote Sensing 11, no. 13: 1536. https://doi.org/10.3390/rs11131536
APA StyleLiu, R., Wen, J., Wang, X., Wang, Z., Li, Z., Xie, Y., Zhu, L., & Li, D. (2019). Derivation of Vegetation Optical Depth and Water Content in the Source Region of the Yellow River using the FY-3B Microwave Data. Remote Sensing, 11(13), 1536. https://doi.org/10.3390/rs11131536