A Priori Solar Radiation Pressure Model for BeiDou-3 MEO Satellites
Abstract
:1. Introduction
2. Precise Orbit Determination for the BeiDou-3 Satellites Using the ECOM1 Model
2.1. ECOM1 SRP Model
2.2. ECOM2 SRP Model
2.3. Precise Orbit Determination Strategies
2.4. D-Acceleration Analysis
3. A Priori SRP for the BeiDou-3 Satellites
3.1. SRP Acceleration Obtained by the Semi-Analytical Model
3.2. Estimation of the A Priori Cuboid SRP Model
4. Validations
4.1. D0 Variation
4.2. Satellite Orbits
4.3. Satellite Clock Offsets
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhao, Q.; Wang, C.; Guo, J.; Wang, B.; Liu, J. Precise orbit and clock determination for BeiDou-3 experimental satellites with yaw attitude analysis. GPS Solut. 2018, 22, 4. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Y.; Li, J.; Yang, C. Progress and performance evaluation of BeiDou global navigation satellite system: Data analysis based on BDS-3 demonstration system. Sci. China Earth Sci. 2018, 61, 614–624. [Google Scholar] [CrossRef]
- Beutler, G.; Brockmann, E.; Gurtner, W.; Hugentobler, U.; Mervart, L.; Rothacher, M.; Verdun, A. Extended Orbit Modeling Techniques at the CODE Processing Center of the International GPS Service for Geodynamics (IGS): Theory and Initial Results. Manuscripta Geodaetica 1994, 19, 367–386. [Google Scholar]
- Deng, Z.; Fritsche, M.; Uhlemann, M.; Wickert, J.; Schuh, H. Reprocessing of GFZ Multi-GNSS Product GBM. In Proceedings of the IGS Workshop 2016, Sydney, Australia, 8–12 February 2016. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS experiment (MGEX) of the International GNSS Service (IGS)–achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Hugentobler, U. Enhanced solar radiation pressure modeling for Galileo satellites. J. Geod. 2015, 89, 283–297. [Google Scholar] [CrossRef]
- Arnold, D.; Meindl, M.; Beutler, G.; Dach, R.; Schaer, S.; Lutz, S.; Prange, L.; Sośnica, K.; Mervart, L.; Jäggi, A. CODE’s new solar radiation pressure model for GNSS orbit determination. J. Geod. 2015, 89, 775–791. [Google Scholar] [CrossRef]
- Prange, L.; Orliac, E.; Dach, R.; Arnold, D.; Beutler, G.; Schaer, S.; Jäggi, A. CODE’s five-system orbit and clock solution the challenges of multi-GNSS data analysis. J. Geod. 2017, 91, 345–360. [Google Scholar] [CrossRef]
- Steigenberger, P.; Montenbruck, O. Galileo status: Orbits, clocks, and positioning. GPS Solut. 2016, 21, 319–331. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Darugna, F. Semi-analytical solar radiation pressure modeling for QZS-1 orbit-normal and yaw-steering attitude. Adv. Space Res. 2017, 59, 2088–2100. [Google Scholar] [CrossRef]
- Zhao, Q.; Chen, G.; Guo, J.; Liu, J.; Liu, X. An a priori solar radiation pressure model for the QZSS Michibiki satellite. J. Geod. 2018, 92, 109–121. [Google Scholar] [CrossRef]
- Wang, C.; Guo, J.; Zhao, Q.; Liu, J. Empirically derived model of solar radiation pressure for BeiDou GEO satellites. J. Geod. 2019, 93, 791. [Google Scholar] [CrossRef]
- Wang, C.; Guo, J.; Zhao, Q.; Liu, J. Solar Radiation Pressure Models for BeiDou-3 I2-S Satellite: Comparison and Augmentation. Remote Sens. 2018, 10, 118. [Google Scholar] [CrossRef]
- Rodriguez-Solano, C.J.; Hugentobler, U.; Steigenberger, P. Adjustable box-wing model for solar radiation pressure impacting GPS satellites. Adv. Space Res. 2012, 49, 1113–1128. [Google Scholar] [CrossRef]
- Rodriguez-Solano, C.J.; Hugentobler, U.; Steigenberger, P.; Allende-Alba, G. Improving the orbits of GPS block IIA satellites during eclipse seasons. Adv. Space Res. 2013, 52, 1511–1529. [Google Scholar] [CrossRef]
- Duan, B.; Hugentobler, U.; Selmke, I. The Adjusted Optical Properties for Galileo/BeiDou-2/QZS-1 Satellites and Initial Results on BeiDou-3e and QZS-2 satellites. Adv. Space Res. 2019, 63, 1803–1812. [Google Scholar] [CrossRef]
- Bury, G.; Zajdel, R.; Sośnica, K. Accounting for perturbing forces acting on Galileo using a box-wing model. GPS Solut. 2019, 23, 74. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Huang, G.; Zhang, Q.; Liu, C.; Wang, L.; Qin, Z. Early analysis of precise orbit and clock offset determination for the satellites of the global BeiDou-3 system. Adv. Space Res. 2019, 63, 1270–1279. [Google Scholar] [CrossRef]
- Xia, L.; Baojun, L.; Yingchun, L.; Sujie, X.; Tao, B. Satellite Geometry and Attitude Mode of MEO Satellites of BDS-3 Developed by SECM; ION GNSS+: Miami, FL, USA, 2018. [Google Scholar]
- Guo, J.; Chen, G.; Zhao, Q.; Liu, J.; Liu, X. Comparison of solar radiation pressure models for BDS IGSO and MEO satellites with emphasis on improving orbit quality. GPS Solut. 2017, 21, 511–522. [Google Scholar] [CrossRef]
- Dilssner, F. A Note on the Yaw Attitude Modeling of BeiDou IGSO-6, a Report Dated November 20, 2017. Available online: http://navigation-office.esa.int/attachments_24576369_1_BeiDou_IGSO-6_Yaw_Modeling.pdf (accessed on 20 February 2019).
- Milani, A.; Nobili, A.M.; Farinella, P. Non-Gravitational Perturbations and Satellite Geodesy; Adam Hilger: Bristol, UK, 1987. [Google Scholar]
- Dow, J.M.; Neilan, R.E.; Rizos, C. The international GNSS service in a changing landscape of global navigation satellite systems. J. Geod. 2009, 83, 689. [Google Scholar] [CrossRef]
- Guo, J.; Xu, X.; Zhao, Q.; Liu, J. Precise orbit determination for Quad-constellation satellites at Wuhan University: Strategy, result validation, and comparison. J. Geod. 2016, 90, 143–159. [Google Scholar] [CrossRef]
- Montenbruck, O.; Schmid, R.; Mercier, F.; Steigenberger, P.; Noll, C.; Fatkulin, R.; Kogure, S.; Ganeshan, A.S. GNSS satellite geometry and attitude models. Adv. Space Res. 2015, 56, 1015–1029. [Google Scholar] [CrossRef] [Green Version]
- Dai, X.; Ge, M.; Lou, Y.; Shi, C.; Wickert, J.; Schuh, H. Estimating the yaw-attitude of BDS IGSO and MEO satellites. J. Geod. 2015, 89, 1005–1018. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction, part II: Refraction corrections in satellite Geodesy. Bull. Geod. 1973, 105, 279–298. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data. Geophy. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef]
- Zhang, R.; Tu, R.; Liu, J.; Hong, J.; Fan, L.; Zhang, P.; Lu, X. Impact of BDS-3 experimental satellites to BDS-2: Service area, precise products, precise positioning. Adv. Space Res. 2018, 62, 829–844. [Google Scholar] [CrossRef]
- Sośnica, K.; Thaller, D.; Dach, R.; Steigenberger, P.; Beutler, G.; Arnold, D.; Jäggi, A. Satellite laser ranging to GPS and GLONASS. J. Geod. 2015, 89, 725–743. [Google Scholar] [CrossRef] [Green Version]
- Urschl, C.; Beutler, G.; Gurtner, W.; Hugentobler, U.; Ploner, M. Orbit determination for GIOVE-A using SLR tracking data. In Extending the Range, Proceedings of the 15th International Workshop on Laser Ranging, Canberra, Australia, 15–20 October 2006; Available online: http://cddis.gsfc.nasa.gov/lw15/docs/papers/Orbit%20Determination%20for%20GIOVE-A%20using%20SLR%20Tracking%20Data.pdf (accessed on 2 July 2019).
- Pavlis, E. SLRF2008: The ILRS reference frame for SLR POD contributed to ITRF2008. In Proceedings of the 2009 Ocean Surface Topography Science Team Meeting, Seattle, WA, USA, 22–24 June 2009. [Google Scholar]
- Huang, G.; Yan, X.; Zhang, Q.; Liu, C.; Wang, L.; Qin, Z. Estimation of antenna phase center offset for BDS IGSO and MEO satellites. GPS Solut. 2018, 22, 49. [Google Scholar] [CrossRef]
- Steigenberger, P.; Fritsche, M.; Dach, R.; Schmid, R.; Montenbruck, O.; Uhlemann, M.; Prange, L. Estimation of satellite antenna phase center offsets for galileo. J. Geod. 2016, 90, 773–785. [Google Scholar] [CrossRef]








| Items | Description |
|---|---|
| Stations | About 17 iGMAS stations and 56 IGS/MGEX stations [5] |
| Time period | From 181 in 2018 to 125 in 2019 |
| Observation | Zero-difference phase and code observations Elevation-dependent weight; Elevation cutoff angle is 15° |
| Data arc | 72-h orbital arcs |
| Attitude model | BeiDou-3: YS mode [25] and CYS mode [21] BeiDou-2: YS mode and ON mode [26] |
| SRP model | ECOM1 () |
| Inter-system biases (ISBs) | A constant parameter per arc for each station, and zero-mean constraints were added for all ISB parameters |
| Ionosphere delay | Ionosphere-free linear combination GPS: L1/L2 BeiDou: B1I/B3I |
| Troposphere model | Zenith total delay: 2-h intervals; SAAS+GMF [27,28]; Horizontal gradients: 6-h intervals |
| Manufacturer | x-offset | y-offset | z-offset |
|---|---|---|---|
| CAST | −200 | 0 | 1500 |
| SECM | −50 | 0 | 800 |
| Surface | Area (m2) | Mass (kg) | |||
|---|---|---|---|---|---|
| Solar panels | 14.100 | 0.72 | 0.00 | 0.28 | 1010 |
| 1.242 | 0.35 | 0.00 | 0.65 | ||
| 1.242 | 0.35 | 0.00 | 0.65 | ||
| 2.576 | 3.748 | 0.35 | 0.00 |
| Surface | Area (m2) | Mass (kg) | |||
|---|---|---|---|---|---|
| Solar panels | 22.704 | 0.72 | 0.00 | 0.28 | 994 |
| 3.748 | 0.35 | 0.00 | 0.65 | ||
| 3.748 | 0.35 | 0.00 | 0.65 | ||
| 3.440 | 3.748 | 0.35 | 0.00 |
| Types | CAST (20,21,22,23,24) | SECM (25,26,27,29,30) | ||
|---|---|---|---|---|
| Parameters | Value | STD | Value | STD |
| 5.99 | 0.11 | 3.02 | 0.01 | |
| −0.32 | 0.02 | 1.05 | 0.01 | |
| −1.18 | 0.11 | 0.84 | 0.08 | |
| 11.10 | 0.21 | 5.61 | 0.03 | |
| −0.53 | 0.01 | 1.95 | 0.01 | |
| 0.21 | 0.08 | 0.05 | 0.02 | |
| 110.62 | 0.69 | 59.01 | 0.81 | |
| PRN | ECOM1 | ECOM2 | Cuboid + ECOM1 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| A | C | R | A | C | R | A | C | R | |
| C20 | 6.98 | 5.14 | 1.30 | 5.92 | 3.77 | 2.56 | 6.18 | 3.68 | 1.56 |
| C21 | 7.26 | 5.42 | 1.42 | 6.21 | 3.77 | 2.15 | 6.16 | 3.80 | 1.54 |
| C22 | 6.90 | 5.78 | 1.38 | 5.81 | 3.77 | 2.44 | 5.98 | 3.70 | 1.50 |
| C23 | 8.98 | 6.58 | 2.10 | 11.31 | 5.75 | 2.96 | 7.32 | 5.86 | 1.78 |
| C24 | 7.84 | 6.44 | 2.04 | 9.83 | 5.33 | 2.79 | 7.12 | 5.38 | 1.70 |
| C25 | 10.04 | 7.68 | 2.20 | 9.13 | 6.56 | 1.98 | 7.96 | 7.00 | 2.02 |
| C26 | 12.34 | 8.36 | 2.48 | 13.52 | 8.25 | 2.79 | 12.00 | 7.84 | 2.64 |
| C27 | 7.82 | 5.94 | 1.54 | 8.40 | 5.33 | 2.71 | 7.66 | 4.76 | 1.38 |
| C28 | 7.56 | 6.04 | 1.66 | 7.43 | 5.57 | 3.43 | 6.06 | 4.56 | 1.38 |
| C29 | 8.02 | 5.80 | 1.58 | 8.33 | 5.23 | 2.71 | 8.40 | 4.48 | 1.52 |
| C30 | 7.96 | 6.06 | 1.80 | 8.15 | 5.56 | 3.06 | 6.84 | 4.44 | 1.34 |
| C32 | 9.50 | 6.00 | 1.94 | 6.77 | 4.96 | 2.88 | 7.06 | 4.46 | 1.50 |
| C33 | 10.48 | 6.72 | 2.04 | 9.27 | 4.94 | 3.31 | 9.76 | 4.76 | 1.84 |
| C34 | 7.84 | 5.68 | 1.60 | 8.60 | 5.83 | 3.23 | 7.10 | 4.72 | 1.04 |
| Avg | 8.54 | 6.26 | 1.79 | 8.56 | 5.31 | 2.74 | 7.54 | 4.96 | 1.62 |
| Manufacturers | x-offset | y-offset | z-offset |
|---|---|---|---|
| SECM | 664.6 | 424.9 | 642.7 |
| CAST | 612.0 | −72.0 | 1223.0 |
| PRN | ECOM1 | ECOM2 | Cuboid + ECOM1 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | STD | RMS | Mean | STD | RMS | Mean | STD | RMS | |
| C20 | −1.38 | 4.86 | 5.05 | −2.13 | 4.12 | 4.64 | −2.77 | 4.02 | 4.88 |
| C21 | −1.42 | 5.28 | 5.47 | −1.77 | 4.46 | 4.80 | −2.36 | 4.16 | 4.78 |
| C29 | −1.60 | 5.49 | 5.72 | −1.34 | 5.23 | 5.39 | −1.05 | 4.24 | 4.37 |
| C30 | −3.06 | 5.87 | 6.62 | −2.20 | 5.15 | 5.60 | −1.64 | 4.52 | 4.81 |
| PRN | ECOM1 | ECOM2 | Cuboid+ECOM1 |
|---|---|---|---|
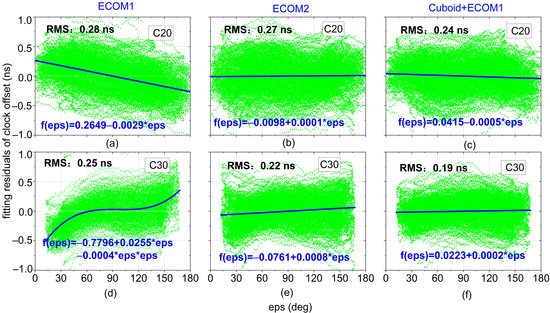
| C20 | 0.28 | 0.27 | 0.24 |
| C21 | 0.31 | 0.29 | 0.28 |
| C22 | 0.34 | 0.35 | 0.32 |
| C23 | 0.26 | 0.27 | 0.27 |
| C24 | 0.21 | 0.22 | 0.21 |
| C25 | 0.39 | 0.39 | 0.39 |
| C26 | 0.33 | 0.31 | 0.31 |
| C27 | 0.22 | 0.22 | 0.18 |
| C29 | 0.24 | 0.22 | 0.19 |
| C30 | 0.25 | 0.22 | 0.19 |
| C32 | 0.21 | 0.21 | 0.19 |
| C33 | 0.27 | 0.29 | 0.24 |
| C34 | 0.27 | 0.26 | 0.24 |
| Avg | 0.27 | 0.27 | 0.25 |
| PRN | ECOM1 | ECOM2 | Cuboid+ECOM1 | |||
|---|---|---|---|---|---|---|
| STD | Mean | STD | Mean | STD | Mean | |
| C20 | 0.13 | 0.34 | 0.13 | 0.33 | 0.11 | 0.28 |
| C21 | 0.12 | 0.36 | 0.12 | 0.31 | 0.11 | 0.33 |
| C22 | 0.12 | 0.40 | 0.13 | 0.32 | 0.11 | 0.30 |
| C23 | 0.21 | 0.35 | 0.20 | 0.34 | 0.19 | 0.37 |
| C24 | 0.17 | 0.41 | 0.17 | 0.34 | 0.14 | 0.34 |
| C25 | 0.25 | 0.34 | 0.19 | 0.38 | 0.21 | 0.32 |
| C26 | 0.25 | 0.32 | 0.21 | 0.34 | 0.23 | 0.26 |
| C27 | 0.16 | 0.40 | 0.16 | 0.32 | 0.14 | 0.31 |
| C29 | 0.16 | 0.37 | 0.16 | 0.38 | 0.14 | 0.33 |
| C30 | 0.18 | 0.39 | 0.16 | 0.35 | 0.14 | 0.33 |
| C32 | 0.18 | 0.36 | 0.16 | 0.28 | 0.15 | 0.32 |
| C33 | 0.18 | 0.42 | 0.19 | 0.32 | 0.19 | 0.32 |
| C34 | 0.16 | 0.34 | 0.18 | 0.25 | 0.13 | 0.24 |
| Avg | 0.17 | 0.37 | 0.17 | 0.33 | 0.15 | 0.31 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Liu, C.; Huang, G.; Zhang, Q.; Wang, L.; Qin, Z.; Xie, S. A Priori Solar Radiation Pressure Model for BeiDou-3 MEO Satellites. Remote Sens. 2019, 11, 1605. https://doi.org/10.3390/rs11131605
Yan X, Liu C, Huang G, Zhang Q, Wang L, Qin Z, Xie S. A Priori Solar Radiation Pressure Model for BeiDou-3 MEO Satellites. Remote Sensing. 2019; 11(13):1605. https://doi.org/10.3390/rs11131605
Chicago/Turabian StyleYan, Xingyuan, Chenchen Liu, Guanwen Huang, Qin Zhang, Le Wang, Zhiwei Qin, and Shichao Xie. 2019. "A Priori Solar Radiation Pressure Model for BeiDou-3 MEO Satellites" Remote Sensing 11, no. 13: 1605. https://doi.org/10.3390/rs11131605
APA StyleYan, X., Liu, C., Huang, G., Zhang, Q., Wang, L., Qin, Z., & Xie, S. (2019). A Priori Solar Radiation Pressure Model for BeiDou-3 MEO Satellites. Remote Sensing, 11(13), 1605. https://doi.org/10.3390/rs11131605