An Improved Hatch Filter Algorithm towards Sub-Meter Positioning Using only Android Raw GNSS Measurements without External Augmentation Corrections

Abstract

In May 2016, the availability of GNSS raw measurements on smart devices was announced by Google with the release of Android 7. It means that developers can access carrier-phase and pseudorange measurements and decode navigation messages for the first time from mass-market Android-devices. In this paper, an improved Hatch filter algorithm, i.e., Three-Thresholds and Single-Difference Hatch filter (TT-SD Hatch filter), is proposed for sub-meter single point positioning with raw GNSS measurements on Android devices without any augmentation correction input, where the carrier-phase smoothed pseudorange window width adaptively varies according to the three-threshold detection for ionospheric cumulative errors, cycle slips and outliers. In the mean time, it can also eliminate the inconsistency of receiver clock bias between pseudorange and carrier-phase by inter-satellite difference. To eliminate the effects of frequent smoothing window resets, we combine TT-SD Hatch filter and Kalman filter for both time update and measurement update. The feasibility of the improved TT-SD Hatch filter method is then verified using static and kinematic experiments with a Nexus 9 Android tablet. The result of the static experiment demonstrates that the position RMS of TT-SD Hatch filter is about 0.6 and 0.8 m in the horizontal and vertical components, respectively. It is about 2 and 1.6 m less than the GNSS chipset solutions, and about 10 and 10 m less than the classical Hatch filter solution, respectively. Moreover, the TT-SD Hatch filter can accurately detect the cycle slips and outliers, and reset the smoothed window in time. It thus avoids the smoothing failure of Hatch filter when a large cycle-slip or an outlier occurs in the observations. Meanwhile, with the aid of the Kalman filter, TT-SD Hatch filter can keep continuously positioning at the sub-meter level. The result of the kinematic experiment demonstrates that the TT-SD Hatch filter solution can converge after a few minutes, and the 2D error is about 0.9 m, which is about 64%, 89%, and 92% smaller than that of the chipset solution, the traditional Hatch filter solution and standard single point solution, respectively. Finally, the TT-SD Hatch filter solution can recover a continuous driving track in this kinematic test.

1. Introduction

As a general impression, we can get a rough position through the consumer-grade chipset in smartphones based on Global Navigation Satellite System (GNSS) observations. The accuracy of the GPS modules embedded in smartphones is typically 3–5 m under good multi-path conditions; otherwise, it can be above 10 m [1]. Meanwhile, previous works have been focusing on different characteristics of GNSS reception and smartphone GNSS performance under different conditions [2,3]. However, as the positioning accuracy of GNSS chipsets improves, the existing devices are likely to be updated and location-based services will become further diversified. Appreciably, achieving positioning and navigation with sub-meter-level accuracy on smart devices with a consumer-grade chipset is an important application for the future development of mass-market GNSS [4]. Therefore, sub-meter-level positioning is urgently required to meet the demands of the high-precision Location Based Services (LBS) [5]. With the release of Android 7, Google announced that the raw GNSS measurements in Android smart devices can be exported and used through the API (Application Programming Interface) at the application level. Thus, it is possible for us to make use of the GNSS raw measurements from the low-cost Android smart terminal for high-precision navigation and positioning. On the other hand, from 2017 to 2020, GNSS receivers in the global market will grow from 5.8 billion to 8.0 billion, in which the smart portable devices that people use almost every day account for almost 80% of the total amount [6]. It means that research on high-precision positioning and navigation of smart devices has great prospects in the market. The official Android documentation illustrates most Android 7.0 or higher smart devices manufactured in 2016 or later can provide raw GNSS data [7].

These GNSS raw measurements from Android devices mainly include the pseudorange, carrier-phase, and Doppler measurements. The pseudorange measurements from the Android-devices combined with broadcast ephemeris can be processed using standard point positioning to provide the user with the meter-level position [8]. Warnant has proposed that carrier phase-based static differential positioning using GPS and Galileo (L1/E1+L5/E5a) on a very short baseline provides cm-level precision in the horizontal component and decimeter-level in the vertical component by using a XiaoMi 8 (XiaoMi, Beijing, China) smartphone [9]. K. Asari used a smartphone-grade antenna and receiver combined with SSR corrections which achieved positioning at the sub-meter level [10]. Meanwhile, D. Calle proposed the MagicPPP method combined with IMU (Inertial Measurement Unit) data from Android-devices, which can reach decimeter-level accuracy [11]. D. Laurichesse developed an application named PPP Wizlite, which can provide positions with a sub-meter level accuracy in static mode and with meter-level accuracy in dynamic mode with online precise satellite corrections [12]. However, a high-precision position obtained by the PPP method needs an online statement and more electric power. Therefore, the point that combines carrier-phase observations with pseudorange observations to attain a high-precision position without any additional corrections for an Android device is worthy of research.

Previous research has found that smoothing the pseudorange measurements with Doppler measurements and carrier-phase measurements can reduce the pseudorange noise and improve the positioning accuracy for the traditional geodetic GNSS receivers [13]. Hatch filter algorithm is a classical phase-smoothed pseudorange algorithm in the existing smoothing filters [14,15]. For the classical Hatch filter algorithm, the selection of the smoothing windows is a difficult and significant step. If the smoothing window is too long, the ionospheric cumulative errors are too large and the filtering will diverge [16]. On the contrary, if the smoothing window is too short, the smoothing effect is not obvious. Park applied an optimal constant to the classical Hatch filter to reduce the ionospheric cumulative errors [17]. Euiho Kim proposed an adaptive carrier smoothing method to weaken the active ionospheric error and severe multipath error [18]. However, there is a big amount of cycle slips in the carrier-phase measurements for Android devices, which is a non-negligible problem for the pseudorange smoothing algorithm as it needs to calculate the phase difference between adjacent epochs. Cycle slips may lead to a devastating influence on the result with the smoothing algorithm [19]. Liu proposed an improved Hatch filter algorithm for the duty-cycle disuse of smartphones [20]. H. K. Lee proposed an improved position-domain Hatch filter, which is advantageous in real-time kinematic positioning and cycle slip detection based on dual frequency observations [21]. Besides, previous research has proposed that for Android smart devices, the clock bias in the carrier phase observation is not the same as the clock bias in the pseudorange observation [22]. Therefore, we construct single-difference observations between satellites to weaken this inequality. In addition, Helena has implemented a fusion filter to combine carrier phase, pseudorange and Doppler to obtain the smoothing position in kinematic tests [23]. In dynamic mode, we use the Kalman filter combined with phase-smoothed pseudorange and Doppler observations for velocity-aided positioning. Based on the above analysis, we will propose an enhanced algorithm based on the Hatch filter and the Kalman filter algorithms, which use variable smoothing window widths dealing with ionospheric delay cumulative errors, cycle slips and outliers in the GNSS observations of Android-devices. Our study is based on the Nexus 9 tablet because it can provide continuous carrier phase observation without duty cycle.

In the following, firstly, the release of GNSS observations after Android N system and the respective data collection applications are briefly reviewed. Secondly, a classical phase-smoothed pseudorange using Hatch filter algorithm and three threshold detections for ionosphere cumulative errors, cycle slips and gross errors of observations from Android devices are discussed, following which the three thresholds-single difference Hatch filter algorithm, i.e., TT-SD Hatch filter algorithm, is proposed. Subsequently, the specific suppression effects of the Three-Thresholds and Single-Difference (TT-SD) Hatch filter algorithm on the ionospheric delay cumulative errors, cycle slips, and outliers, are verified by experiments. In the next section, the quality analyses of pseudorange and carrier-phase observations are discussed and the experiment design, results, and experimental analysis are outlined. Finally, the discussion and conclusions are presented.

2. Methods

2.1. Acquisition of GNSS Measurements

Although we can acquire raw GNSS information, we cannot obtain the pseudorange and carrier-phase measurements directly from Android devices through the API at the application level. We should first carry on a series of transformations on the parameters provided with the corresponding APIs to obtain the pseudorange and carrier-phase measurements. The reception time of the GNSS signal in the GPS time system $t_{Rx}$ is computed as:

$$t_{Rx}=TimeNanos-\left(FullBiasNanos+BiasNanos\right)\left(ns\right)$$

(1)

where TimeNanos denotes the GNSS receiver internal hardware clock value in nanoseconds; FullBiasNanos denotes the difference between the hardware clock inside the GPS receiver and the true GPS time since 6 January 1980 (GPS time start reference); and BiasNanos denotes the clock sub-nanosecond bias [24]. After computing the reception time in the GPS time system, the pseudorange $P$ can be deduced using Equation (2):

$$P=(t_{Rx}-t_{Tx})\ast c$$

(2)

where $c$ is the speed of light and $t_{Tx}$ is the transmitted time of the GPS signal in the GPS time system calculated by the getReceivedSvTimeNanos function of Android API 24 [24].

Meanwhile, we can derive carrier-phase measurements from the AccumulatedDeltaRangeMeters observations calculated by the getAccumulatedDeltaRangeMeters function of Android API 24. The mathematical relationship between the AccumulatedDeltaRangeMeters parameter and carrier-phase measurement is expressed by the following equation:

$$AccumulatedDeltaRangeMeters=-k\ast (\mathit{\text{carrier-phase}})$$

(3)

where $k$ is the wavelength of carrier-phase data. The Doppler shift that results from satellite movement can be derived from the getPseudorangeRateMetersPerSecond function of Android API 24 in m/s [24].

We used the data collection applications GnssLogger (V 2.0.0.1 Release) to collect the raw GNSS data, [25] whilst the collected raw GNSS data are processed and converted into the RINEX 3.0 format by our own software.

2.2. Phase-Smoothed Pseudorange

Phase-smoothed pseudorange can decrease the noise of pseudorange. Among all the smoothing techniques, the Hatch filter is a type of recursive filter that uses the current measurement and previous estimate without any dynamic model or additional sensors, and it can be implemented for real-time operation in a low-cost single-frequency GNSS receiver [16]. The equation of the Hatch filter is as follows:

$$\{\begin{array}{l}\overline{P}(n)=\frac{1}{n}P(n)+\frac{n-1}{n}(\overline{P}(n-1)+\Phi (n)-\Phi (n-1))\\ \overline{P}(1)=P(1)\end{array}$$

(4)

where $\Phi (n)$ and $\Phi (n-1)$ denote the carrier-phase observation at $n\mathrm{th}$ and $(n-1)\mathrm{th}$ epoch, respectively; $\overline{P}(n)$ and $\overline{P}(n-1)$ denote the smoothed pseudorange at the $n\mathrm{th}$ and $(n-1)\mathrm{th}$ epoch, respectively; and $P(n)$ denotes the pseudorange measurement at the $n\mathrm{th}$ epoch. Through Equation (4) we can find that as the measured values increase, the pseudorange will be smoothed and measurement noise will be decreased. As the single difference between epochs is used, ambiguity has been subtracted when no cycle slips occur.

Previous research has proposed that for Android devices, the receiver clock bias in the carrier phase raw observation may not be the same as the clock bias in the pseudorange [22]. To avoid the possible influence of this inequality, we use the single difference between satellites. Therefore, we establish the smoothed pesudorange observations with a single difference between satellites based on the Hatch filter smoothing algorithm, as described in Equation (5):

$$\{\begin{array}{l}{\overline{P}}^{s,A}(\mathrm{n})=\frac{1}{n}{P}^{s,A}(n)+\frac{n-1}{n}({\overline{P}}^{s,A}(n-1)+{\Phi }^{s,A}(n)-{\Phi }^{s,A}(n-1))\\ P^{s,A}=P^s-P^A\\ {\Phi }^{s,A}={\Phi }^s-{\Phi }^A\\ {\overline{P}}^{s,A}(1)=P^{s,A}(1)\end{array}$$

(5)

where $A$ and $s$ represent the reference satellite and the non-reference satellite, respectively; $P^A$ and $P^s$ denote the raw pseudorange observations of satellites $A$ and $s$, respectively, while ${\Phi }^A$ and ${\Phi }^s$ denote the raw carrier-phase observation of satellites $A$ and $s$; and $P^{s,A}$, ${\overline{P}}^{s,A}$ and ${\Phi }^{s,A}$ denote the single difference raw pseudorange, smoothed pseudorange and carrier-phase observation between the reference satellite $A$ and the non-reference satellite $s$, respectively. Besides, in our algorithm, we choose the satellite with the highest elevation as the reference satellite.

2.3. Threshold Detection for Ionosphere Delay Cumulative Error

The observation equation for single-difference pseudorange and carrier-phase between satellites is:

$$\{\begin{array}{l}{P}^{s,A}={\rho }^{s,A}-cd{T}^{s,A}+I^{s,A}+T^{s,A}+{\epsilon }_{P^{s,A}}\\ {\Phi }^{s,A}={\rho }^{s,A}-cd{T}^{s,A}-I^{s,A}+T^{s,A}+\lambda N^{s,A}+{\epsilon }_{{\Phi }^{s,A}}\end{array}$$

(6)

In the above equations, ${\Phi }^{s,A}$ is the single difference carrier-phase observation; ${\rho }^{s,A}$ is the single difference distance between the satellite and receiver; $d{T}^{s,A}$ is the single difference satellite clock bias between the reference satellite $A$ and the non-reference satellite $s$; $I^{s,A}$ and $T^{s,A}$ represent the single difference propagation delay of the ionosphere and troposphere; and ${\epsilon }_{P^{s,A}}$ and ${\epsilon }_{{\Phi }^{s,A}}$ are the sum of all remaining errors of single difference pseudorange and carrier phase respectively. Based on Equation (6), we use the epoch-differenced method between $n\mathrm{th}$ and $(n-1)\mathrm{th}$ epoch and the transformed observation equation can be described in Equation (7):

$$\{\begin{array}{l}{P}^{s,A}(n)-P^{s,A}(n-1)={\rho }^{s,A}(n, n-1)-cd{T}^{s,A}(n, n-1)+I^{s,A}(n, n-1)+T^{s,A}(n, n-1)+{\epsilon }_{P^{s,A}}\\ {\Phi }^{s,A}(n)-{\Phi }^{s,A}(n-1)={\rho }^{s,A}(n, n-1)-cd{T}^{s,A}(n, n-1)-I^{s,A}(n, n-1)+T^{s,A}(n, n-1)+{\epsilon }_{{\Phi }^{s,A}}\end{array}$$

(7)

Although the Hatch filter performs excellently in reducing noise and is easy to implement under normal conditions, the ionosphere-related term should not be ignored and should be compensated in the phase-smoothed pseudorange as described:

$${\Phi }^{s,A}(n)-{\Phi }^{s,A}(n-1)=P^{s,A}(n)-P^{s,A}(n-1)-2\cdot I^{s,A}(n, n-1)$$

(8)

Equations (5) and (8) show that as the observation time increases, the ionosphere delay errors are gradually accumulated in Hatch filter processing. In order to reduce the influence of the ionosphere delay cumulative errors, it needs to reset the window and re-smooth observations when this error exceeds the pseudorange measurement range. We use the difference between the smoothed pseudorange and the raw pseudorange to detect whether the ionosphere delay cumulative errors reach the threshold and reset the filter window:

$$\left|{\overline{P}}^{s,A}(\mathrm{n})-P^{s,A}(\mathrm{n})\right|<{\xi }_1$$

(9)

where ${\xi }_1$ denotes the detection threshold and ${\xi }_1=3\times 2{\sigma }_P$ is set according to the 3σ-Rule and variance-covariance propagation law, where ${\sigma }_P$ is the standard deviation of pseudorange measurement error.

2.4. Threshold Detection for Cycle Slip

Based on the collected GPS data from Nexus 9 and Trimble NetR9 (Trimble, Sunnyvale, CA, USA) receiver over 24 h, we make an assessment of the number of cycle slips for the carrier-phase observations. Figure 1 shows that there exists a huge number of cycle slips in the whole time series of carrier phase observations for Nexus 9 device, which is about 18 times as many as that for Trimble NetR9 receiver. This is because the GNSS antenna used for the Android-device Nexus 9 is a low-cost linearly polarized antenna with poor multipath resistance. In addition, the price of the GNSS chipset in Nexus 9 is relatively low, and the quality of the phase-locked loop is worse than that of the traditional GNSS geodetic receiver. Therefore, there are a large number of cycle slips which jeopardize the phase-smoothed pseudorange in real time or in post-processing mode.

In order to mitigate the influence of cycle slips, we perform cycle slip detection by the relationship between Doppler and phase change rate. When a cycle slip occurs, the phase-smoothed pseudorange window is reset to re-smooth observations. The cycle slip detection and threshold are designed as follows [26]:

$$\left|\left(\Phi (n)-\Phi (n-1)\right)+\frac{D(n)+D(n-1)}{2}\Delta t\right|<{\xi }_2$$

(10)

where $D(n)$ and $D(n-1)$ represent the Doppler observations at $n\mathrm{th}$ and $(n-1)\mathrm{th}$ epoch, respectively; $\left(\Phi (n)-\Phi (n-1)\right)$ represents the phase change rate by single difference between the $n\mathrm{th}$ and $(n-1)\mathrm{th}$ epoch; $\Delta t$ denotes time interval; and ${\xi }_2$ denotes the cycle slip threshold, which is valued as one cycle when $\Delta t$ is 1 s.

2.5. Threshold Detection for Outliers

As we know, if the outliers (such as observation biases) in the GNSS observations cannot be accurately detected and properly removed, the pseudorange smoothing may be seriously affected or even fail. We use the difference between the pseudorange rate and the phase rate to detect outliers. The difference between $(P(n)-P(n-1))$ and $\left(\Phi (n)-\Phi (n-1)\right)$ is $2\cdot I(n, n-1)$, and the epoch-difference ionospheric delay $I(n, n-1)$ is much smaller. When an outlier occurs in the pseudorange or phase, a large number is introduced. Therefore, we set the following threshold detection:

$$\left|(P(n)-P(n-1))-\left(\Phi (n)-\Phi (n-1)\right)\right|<{\xi }_3$$

(11)

where ${\xi }_3$ denotes the detection threshold and ${\xi }_3=3\times \sqrt{2}{\sigma }_P$ is set according to the 3σ-Rule and variance-covariance propagation law, where ${\sigma }_P$ is the standard deviation of pseudorange measurement error.

2.6. Three-Thresholds and Single-Difference Hatch Filter Algorithm

Based on the above analysis, we eliminate the receiver clock inconsistency between the pseudorange and the phase by the single difference between the satellites. Meanwhile, we introduce these three threshold detections into the Hatch filter to adaptively adjust the smoothing window length, in order to weaken the influence of the ionosphere cumulative errors, cycle slips, and gross errors. Therefore, we call this method: three thresholds–single difference Hatch filter algorithm (TT-SD Hatch-Filter). Figure 2 presents the whole process of the algorithm.

In detail, the processing procedures of our TT-SD Hatch filter include:

• Input raw GNSS (Global Navigation Satellite System) observations;
• Form a single-difference carrier phase and pseudorange observations between the reference satellite and non-reference satellite;
• Phase-smoothed pseudorange by Hatch filter;
• Three thresholds detection: While the difference between the smoothed pseudorange and true pseudorange (t₁) is less than the threshold (ξ₁) for ionosphere delay cumulative errors, the phase rate prediction residual by Doppler observations (t₂) is less than the threshold (ξ₂) for the cycle slip, and the difference between the pseudorange rate and the phase rate (t₃) is less than the threshold (ξ₃) for outliers; the smoothing window width accumulates and the smoothed pseudorange observations are available for positioning. Otherwise, the smoothing window is re-initialized.
• If the smoothing window was initialized and the condition t₃ < ξ₃ holds, the raw pseudorange observations are used for positioning, or else no pseudorange observations are available for positioning at this epoch.
• Repeat step 1–5 above for all epochs of GNSS observations to obtain the smoothed pseudorange observations for positioning.

2.7. Three-Thresholds and Single-Difference Hatch Filter Algorithm with Kalman Filter

In the process of obtaining a smoothed pseudorange using the TT-SD Hatch filter algorithm, if any one of the thresholds is exceeded, the smoothing window will be reset and the continuity between the epochs for the position parameters will be destroyed. In particular, the frequent occurrence of cycle slips and outliers in Android devices makes this problem more serious. Therefore, we use the Kalman filter for state update and measurement update to obtain smoothed position results. When the user is in the kinematic mode, the Doppler observations are used to estimate the velocity of the user, which is combined with the position of the user to construct the state vector of the system. The position of the user is only estimated on the static mode. The recurrence model is described as Equation (12):

$$X_k={\mathsf{\phi }}_{k,k-1}{X}_{k-1}+Q_k$$

(12)

where $k$ denotes the $k\mathrm{th}$ epoch; $X$ denotes the state vector of the receiver; $\phi$ denotes the state transition matrix between epochs; and $Q$ denotes the processing noise vector. When applying the kinematic mode, assuming $T$ is the sampling interval, $X$, $\mathsf{\phi }$ and $Q$ can be described as:

$$X=\left[\begin{array}{c}r\\ \begin{array}{l}V\\ a\end{array}\end{array}\right],\mathsf{\phi }=\left[\begin{array}{ccc}I& T& \frac{T^2}{2}\\ 0& I& T\\ 0& 0& I\end{array}\right],r=\left[\begin{array}{c}x\\ y\\ z\end{array}\right],v=\left[\begin{array}{c}{v}_x\\ v_y\\ v_z\end{array}\right],a=\left[\begin{array}{c}{a}_x\\ a_y\\ a_z\end{array}\right],Q=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& q_a\end{array}\right]$$

(13)

where $r$, $V$ and $a$ denote the vector of position, velocity, and accelerometer of the receiver, respectively; and $q_a$ denotes the processing noise of the accelerometer, which usually denotes a diagonal matrix. When applying the static mode, different from Equation (13), $X$, $\phi$ and $Q$ can be described as:

$$X=\begin{array}{c}r\end{array},\mathsf{\phi }=\begin{array}{c}I\end{array},r=\left[\begin{array}{c}x\\ y\\ z\end{array}\right],Q=\begin{array}{c}{q}_r\end{array}$$

(14)

The state vector only includes the position $\begin{array}{c}r\end{array}$ of the receiver. $q_r$ denotes the processing noise of the position. The clock bias and the clock rate of the receiver are not included in the state vector $X$, because the single difference between satellites eliminates the influence of clock bias and clock rate; $I$ denotes a 3 × 3 unit matrix. Besides, in our algorithm, we have set the initial state error covariance matrix of position as described:

$$P_r=\left[\begin{array}{ccc}Va{r}_{\mathrm{x}}& 0& 0\\ 0& Va{r}_y& 0\\ 0& 0& Va{r}_z\end{array}\right]$$

(15)

where $Va{r}_{\mathrm{x}}$, $Va{r}_y$ and $Va{r}_z$ represent the error covariance of the position of user $[xyz]$. Meanwhile, in kinematic mode, the initial state error covariance matrix of velocity and acceleration as described:

$$P_v=\left[\begin{array}{ccc}Va{r}_{v_x}& 0& 0\\ 0& Va{r}_{v_y}& 0\\ 0& 0& Va{r}_{v_z}\end{array}\right],P_a=\left[\begin{array}{ccc}Va{r}_{a_x}& 0& 0\\ 0& Va{r}_{a_y}& 0\\ 0& 0& Va{r}_{a_z}\end{array}\right]$$

(16)

where $Va{r}_{v_x}$, $Va{r}_{v_y}$ and $Va{r}_{v_z}$ represent the error covariance of the velocity of the user $[v_x{v}_y{v}_z]$; $Va{r}_{a_x}$, $Va{r}_{a_y}$ and $Va{r}_{a_z}$ represent the error covariance of the acceleration of the user $[a_x{a}_y{a}_z]$.

The predicted covariance matrix can be calculated with $P_{k-1|k-1}$ using the following equation:

$$P_{k|k-1}={\phi }_k{P}_{k-1|k-1}{{\mathsf{\phi }}_k}^T+Q_k$$

(17)

After computing the gain matrix $K_k$, the matrix $P_{k|k}$ can be updated. $H_k$ denotes the design matrix. $R_k$ is the covariance matrix of observation noise.

$$\begin{array}{l}{K}_k=P_{k|k-1}{H_k}^T{(H_k{P}_{k|k-1}{H_k}^T+R_k)}^{-1},\\ P_{k|k}=(I-K_k{H}_k)P_{k|k-1}\end{array}$$

(18)

The smoothed inter-satellite difference pseudorange and Doppler observation equations are described as:

$${{\overline{P}}_k}^{s,A}={\rho }_k^{s,A}-\mathrm{c}\ast d{T}^{s,A}+I^{s,A}+T^{s,A}+{\epsilon }_{{P_k}^{s,A}}$$

(19)

$$\lambda D_k^{s,A}={\dot{\rho }}_k^{s,A}-c\ast d{\dot{T}}^{s,A}+{\epsilon }_{D_k^{s,A}}$$

(20)

where $s$ and $A$ denote the non-reference satellite and reference satellite, respectively; ${\overline{P}}_k^{s,A}$ denotes the smoothed inter-satellite difference peseudorange after TT-SD Hatch filter processing at epoch $k$; ${\rho }_k^{s,A}$ and ${\dot{\rho }}_k^{s,A}$ denote the inter-satellite difference range and range-rate between the receiver and the satellites $s$, $A$; $\lambda$ and $D_k^{s,A}$ respectively denote the wavelength of L1 signal and inter-satellite difference Doppler observation; $d{\dot{T}}^{s,A}$ denotes the inter-satellite difference satellite clock bias rate. In addition, $I^{s,A}$ and $T^{s,A}$ are corrected by the Klobuchar and Saastamoinen models, respectively [27,28].

For the kinematic mode, the measurement formula in our system can be described in Equation (21):

$$Z_k=H_k{X}_k+{\nu }_k,Z_k=\left[\begin{array}{c}{{\overline{P}}_k}^{s,A}\\ \lambda D_k^{s,A}\end{array}\right],H_k=\left[\begin{array}{cccccc}({l_k}^a-l_k{}^A)& (m_k{}^a-m_k{}^A)& ({n_k}^a-{n_k}^A)& ({l_k}^a-{l_k}^A)& ({m_k}^a-{m_k}^A)& ({n_k}^a-{n_k}^A)\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ (l_k{}^s-l_k{}^A)& (m_k{}^s-m_k{}^A)& (n_k{}^s-n_k{}^A)& (l_k{}^s-l_k{}^A)& (m_k{}^s-m_k{}^A)& (n_k{}^s-n_k{}^A)\end{array}\right]$$

(21)

where $Z_k$ denotes the measurement vector; $H_k$ denotes the design matrix, in which index $a$ to $s$ denote non-reference satellite and $A$ denotes reference satellite; $[l_k^a{m}_k^a{n}_k^a]$, $[l_k^s{m}_k^s{n}_k^s]$ and $[l_k^A{m}_k^A{n}_k^A]$ denote direction cosine vector between the satellite and receiver for satellites $a$, $s$ and $A$, respectively; ${\mathsf{\nu }}_k$ denotes the measurement noise, which depends on the smoothing window width and the signal to noise ratio of the observations [29]. For the static mode, different from Equation (21), the measurement formula is described as:

$$Z_k=H_k{X}_k+{\mathsf{\nu }}_k,Z_k={{\overline{P}}_k}^{s,A},H_k=\left[\begin{array}{ccc}({l_k}^a-{l_k}^A)& ({m_k}^a-{m_k}^A)& ({n_k}^a-{n_k}^A)\\ ⋮& ⋮& ⋮\\ ({l_k}^s-{l_k}^A)& ({m_k}^s-{m_k}^A)& ({n_k}^s-{n_k}^A)\end{array}\right]$$

(22)

The flowchart of our positioning algorithm is shown in Figure 3. Firstly, the GNSS observations obtained by smartphones are pre-processed by TT-SD Hatch-filter algorithm to obtain the smoothed pseudorange. Secondly, either kinematic or static processing mode is selected by the user. Thirdly, after processing with the Kalman filter algorithm, the estimated parameters, such as position and velocity are generated.

3. Results

In this part, firstly we make algorithm validation with survey-grade receivers to verify the specific suppression effect of the three threshold detections on the ionosphere delay cumulative error, cycle slip and outliers. Secondly, we make a quality assessment for Nexus 9 Raw GNSS data to verify that the pseudorange noise of the Nexus 9 tablet can be reduced by phase-smoothed pseudorange. Finally, GNSS chipset solution inner Nexus 9 tablet, single point positioning solution by software RTKLIB and traditional Hatch filter solution as comparisons are used to compare the accuracy of the result accessed by TT-SD Hatch filter algorithm in static test and kinematic test, respectively.

3.1. Algorithm Validation with Survey-Grade Receivers

In order to verify the specific suppression effect of the TT-SD Hatch filter method on the ionosphere delay cumulative error, cycle slip and outliers, we used 1-hour continuous GPS observations without cycle slips and outliers. Since it is difficult for Android devices to provide raw observations without cycle slips and outliers within 1 hour, we use the GPS observations from the Trimble NetR9 with a sampling interval of 1 s. We stress that there are no cycle slips or outliers in the observations in order to separate the effects of cycle slips or outliers from ionosphere delay cumulative error and to prevent two validation experiments from interfering with each other. Because the TT-SD Hatch filter method will reset the smooth window in any of the above three cases.

Figure 4 shows that the ionosphere accumulative errors are particularly significant when the Hatch filter is with a large smoothing window. The pseudorange residuals of the traditional Hatch filter with 3600s-window solution increases as smoothing time increases until the smoothing window is reset. However, both the traditional Hatch filter with a 600s-window solution and TT-SD Hatch filter solution can provide a more precise position with less ionosphere accumulative errors, because they reset the smoothing window more reasonably and frequently. The change rate of the pseudorange residual of TT-SD Hatch filter solution is different from that of the traditional Hatch filter with a 600s-window solution. It is because the TT-SD Hatch filter performs the inter-satellite difference, which makes the change rate of ionospheric delay error different from or even lower than that of a traditional Hatch filter.

To assess the performance of the TT-SD Hatch filter method on suppressing the cycle slips and outliers, we add some simulated cycle slips and outliers in the real GPS data. They are marked as the black ovals in the bottom panel of Figure 5. From left to right, the black ovals represent the simulated pseudorange outliers of 30 m, phase outliers of 15 cycles, cycle slips of 3 cycles, cycle slips of 100 cycles, pseudorange outliers of 3 m, and phase outliers of 2 cycles. In this test, as the receiver clock bias in pseudorange observations and phase observations are always regarded as the same for the geodetic receiver, we have not formed an inter-satellite difference pseudorange in TT-SD Hatch filter to smooth pseudorange observations in order to make a comparison with the smoothed pseudorange by a traditional Hatch filter. Figure 5 shows that both the traditional Hatch filter with 600s-window and the TT-SD Hatch filter can effectively smooth the pseudorange without the cycle slips and outliers, and the pseudorange measurement noise is significantly reduced. However, when there are cycle slips or outliers in the observations, the result of the Hatch filter with a 600s-window is seriously degraded. Specifically, when the observation contains a large pseudorange or phase outlier, such as a pseudorange outlier of 30 m or phase outlier of 15 cycles in the bottom panel of Figure 5, an error is introduced into the smoothed pseudorange of the Hatch filter with 600s-window solution, as shown in the illustrations a and b. The carrier phase outlier only affects the smoothed pseudorange of the current epoch. However, the pseudorange outlier will affect all the smoothed pseudoranges after the epoch. When the pseudorange outlier occurs early in the smoothing window, the effect on the smoothed pseudorange become greater. Unfortunately, the cycle slips have a more significant impact on the traditional Hatch filter. When the cycle slip occurs, a systematic bias, proportional to the magnitude of the cycle slips, will be introduced into the smoothed pseudorange until the smooth window is reset. For example, when a cycle slip of three cycles is introduced, the smoothed pseudorange residual is increased by about 0.6 m. However, when a cycle slip of 100 cycles is introduced, the smoothed pseudorange residual is increased to 20 m. Even worse, the smoothed pseudorange residuals of the subsequent epochs are all over 10 m until the smoothing window is reset. Therefore, the traditional Hatch filter requires additional processing to eliminate the effects of cycle slips and outliers. Fortunately, the proposed TT-SD Hatch filter can sensitively detect all cycle slips or outliers of the pseudorange and phase data in this test, and automatically reset the smoothing window in time. It is worth noting that no smoothed pseudorange is output when a pseudorange outlier occurs, and the smoothed pseudorange is replaced by raw pseudorange when the cycle slips or phase outliers occur.

For Android-devices such as Nexus 9 tablet, the smoothing window will be frequently initialized by plenty of cycle slips and outliers, and the continuity of the state parameters between epochs is destroyed. Therefore, we introduce the Kalman filter to establish the state-updated equation. Specifically, when cycle slips or outliers occur, the smoothing window will be re-initialized. Meanwhile, the state parameters will be updated only relying on the previous state parameters to maintain the stability of state parameters. Thus, in the static case, the state parameter is used to predict the next state parameter directly. While in the dynamic case, Doppler observations are introduced for velocity measurement, and status update is performed accordingly.

3.2. Quality Assessment for Nexus 9 Raw GNSS Data

The Nexus 9 tablet embeds a Broadcom BCM4752 GNSS receiver module, which is capable of tracking GPS and GLONASS signals. Nevertheless, in this study, only GPS observations were used. In our static experiment, all devices were located on the rooftop of a 16th-story building in Wuhan University, as shown in Figure 6. The Trimble NetR9 receiver equipped with the high-quality Trimble antenna can meet the needs of our experiment as a reference station, and the antenna is fixed at about 0.5 m apart from the Nexus 9 tablet device. GPS data are continuously observed for 1 day with a sampling interval of 1 s.

Figure 7 shows that the standard deviation of the pseudorange noise for Nexus 9 is about 4 m, which is much larger than that of the Trimble NetR9 receiver. However, the noise of carrier-phase observations of the Nexus 9 tablet is close to that of Trimble NetR9 receiver, and the standard deviation of both solutions is less than 0.05 cycles. Therefore, we can reduce the pseudorange noise of the Nexus 9 tablet by phase-smoothed pseudorange. It should be noted that the pseudorange and carrier phase noise of the Nexus 9 Android-device contain more noise than that of the geodetic receiver. This may be caused by outliers or cycle slips. Therefore, the influence of cycle slips and outliers should be considered when using the phase-smoothed pseudorange for Android devices.

3.3. Static Test Using Nexus 9 Raw GNSS Data

As shown in Figure 6, we carried on a static test with the Nexus 9 tablet placed on a designed board and we analyzed the quality for the raw measurements of the static test according to the SNR, PDOP and satellite number results. The two patch antennas were placed in zone A and C respectively, while the Nexus 9 tablet was placed in zone B. Each patch antenna was connected with a μblox-M8T receiver, which was used to provide the reference position for Nexus 9 tablet. According to the SNR results, we can find that most of the values are between 30 and 40 dBHz. That is the level which the smart device can reach in the open-sky environment. When it comes to the satellite numbers and the PDOP values, the satellite numbers are around 8 and most PDOP values are less 2. In addition, when the available satellite number decreases, the satellite geometry will be worse so that the PDOP value will become larger. Fortunately, it can ensure that in most cases it can meet the requirement of measurement updating by using the single difference values of the pseudorange observations.

Since it is almost impossible to find the phase center of the Nexus 9 tablet, the midpoint of the two patch antennas was regarded as the approximate reference positions of the Nexus 9 tablet. Each patch antenna and a nearby reference station were used to form a short baseline of less than 1 m. The positions of the A and C patch antennas are obtained by short baseline relative positioning, and their ambiguity resolution success rates are 98.2% and 99.5%, respectively. In the static test, the GNSS observations collected with Nexus 9 tablet were processed with TT-SD Hatch filter algorithm combined with Kalman filter in static processing mode, single point positioning algorithm (SPP) mode by GNSS processing software RTKLIB (T. Takasu, Japan, 2.4.2 version), and SPP mode based on traditional Hatch filter with a 600s-window to smooth inter-satellites difference pseudorange measurements. In addition, the GNSS chipsets positioning results of Nexus 9 were offline outputs for comparisons. The time series of positioning errors of our processing and the chipset position of Nexus 9 in the east, north and up direction are shown in Figure 8.

In the experiment, for all the methods, only GNSS raw observations and broadcast ephemeris were used for positioning, where no additional information was needed. The chipset positioning solution is processed by the corresponding API supported by the GPS location provider at the application level. It is widely used by smartphone applications in the mass market in offline condition. The chipset position is estimated based on the Kalman filter provided by the GPS chipset [25].

Figure 8 and

Table 1. Comparison of static positioning errors in terms of RMS.

	East (m)	North (m)	Up (m)
TT-SD Hatch filter solution	0.357	0.447	0.840
Chipset Solution	1.257	2.300	2.488
Traditional Hatch filter solution	6.543	8.707	10.203
RTKLIB SPP solution	7.803	10.065	12.667

indicate that the horizontal and vertical positioning errors of the chipset solution are approximately 2.6 m and 2.5 m in terms of RMS. It is worth noting that in Table 1, the positioning results with gross errors larger than 30 m were excluded from the statistics of traditional Hatch filter solution and RTKLIB SPP solution. In addition, the position errors obviously vary with time, even in an open environment. As expected, the horizontal and vertical positioning errors of the TT-SD Hatch filter solution are kept at approximately 0.6 m and 0.8 m, respectively, after taking a few minutes to convergence. Conversely, both the RTKLIB SPP solution and the traditional Hatch filter solution have larger positioning errors, and the RMS is larger than 10 m in the horizontal and vertical components. It is noted that in some cases, the time series of position solutions derived from traditional Hatch filters are much smoother and have lower noise, such as the smoothing results in the first 10 min. However, after 10 min, i.e., within the second smoothing window, the subsequent smooth pseudoranges are invalid due to large cycle-slips or gross errors of the observations. Therefore, in these cases, the smoothing pseudorange is invalid, and only the raw pseudorange can be used for positioning. As a result, the result similar to that of SPP solution can be obtained. In contrast, our TT-SD Hatch filter algorithm can successfully detect the cycle slips and outliers and reset the smoothed window in time. Meanwhile, with the aid of the Kalman filter, the TT-SD Hatch filter can achieve continuous positioning with steady accuracy.

3.4. Kinematic Test Using Nexus 9 Raw GNSS Data

In the kinematic test, we placed the Nexus 9 tablet and two patch antennas connected with two μblox-M8T receivers on the roof of a car, as shown in Figure 9. Besides, we set up a geodetic antenna connected with Trimble NetR9 receiver on a fixed tripod, which was located in an open-sky condition as the reference station. The reference position of the Nexus 9 tablet is obtained in the same way as the static test, which is the midpoint of A and C patch antennas. The baseline length of patch antennas on the roof and the reference station are less than 600 m. The positions of the A and C patch antennas are obtained by short baseline relative positioning, and their ambiguity success rates are 88.2% and 87.7%, respectively. The experimental area is in Wuhan suburb, which is in an open-sky condition except for several minutes of shielding from trees and buildings, as shown in Figure 10. GPS data were collected continuously with a sampling interval of 1 s. Similar to the static experiments, broadcast ephemeris was used to process the GNSS raw observations.

Figure 10 shows that compared with the chipset solution track, the TT-SD Hatch filter track was smoother and agreed better with the reference track. In addition, we also analyzed the quality for the raw measurements of the kinematic test. According to the SNR results, we can find that most of the values are between 20 and 35 dBHz. They are worse than the results of the static test and the time series are intermittent. This is because in the kinematic test, the observation environment is poor, and some tall buildings and trees block the signals so that the quality of the raw data is reduced. As for the satellite numbers and the PDOP values, the satellite numbers are around 8 and the PDOP values are around 2. The satellite number is enough, however, the variation is not very stable. When the car turned around, i.e., the red zones circled presented in Figure 10, the position of the GNSS chipset solution diverged from the reference track, but the TT-SD track still coincided well with the reference track. Meanwhile, Figure 11 shows that both the SPP and traditional Hatch filter solutions perform a high-level of error noise and they hardly recovered the whole driving track, compared to the two solutions in Figure 10. Therefore, TT-SD Hatch filter does perform better than the other methods mentioned above, which can recover the entire driving track continuously in the kinematic test. The statistics of these four solutions are presented in Figure 12 and

Table 2. RMS of the 2D positioning error of four solutions in kinematic experiments.

	2D-RMS(m)
TT-SD Hatch filter solution	0.953
Chipset solution	2.644
Traditional Hatch filter solution	8.961
RTKLIB SPP solution	11.334

.

Figure 12 shows that after a few minutes to convergence, the 2D error of TT-SD Hatch filter solution is generally at the submeter-level, while that of chipset solution is of instability. Meanwhile, Figure 12 shows that both the RTKLIB SPP solution and SPP solution by traditional Hatch filter with 600s-window to smooth inter-satellites difference pseudorange measurements have much higher measuring noises and more gross errors, compared to the TT-SD Hatch-Filter solution. It can be concluded from Table 2 that TT-SD Hatch filter algorithm on kinematic mode can achieve a more accurate positioning than the other three solutions. The 2D-RMS positioning errors of TT-SD Hatch filter are 0.953 m, which is improved by about 64% and 89% compared to the chipset solution and the traditional Hatch filter solution.

4. Discussion

Based on the proposed TT-SD filter method, we can achieve sub-meter positioning accuracy in dynamic and static environments by using only Android raw GNSS measurements without external augmentation corrections. However, the raw GNSS observations from Android devices are seriously affected by multipath errors, which will also seriously affect the final positioning accuracy. Banville and Diggelen (2016) pointed out that the passive linear polarized embedded GNSS antennas were the main culprit for this issue, and an external antenna might be a solution [8]. Geng et al. (2018) replaced the embedded GNSS antenna of a Nexus 9 tablet with an external survey-grade GNSS antenna [30]. The strength of the GNSS signal obtained by them was consistent with that of the survey-grade receivers; and the multipath errors, cycle slips and outliers in the raw GNSS observations were rare. As a result, the influence of frequent re-initialization of the TT-SD smoothing window caused by a large number of cycle slips and outliers will be reduced, and more accurate positioning results can be obtained for Android devices using our TT-SD filter algorithm.

In addition, in this paper, the TT-SD filter algorithm is designed based on single-frequency GPS data of Android devices, because single-frequency GPS data are mostly provided by mainstream Android devices. On 31 May 2018, XiaoMi 8, the world’s first dual-frequency GNSS smartphone, was launched. It is equipped with a Broadcom BCM47755 chipset, which can provide dual-frequency (L1/E1 + L5/E5) raw GNSS observations [31,32]. Thanks to the dual-frequency observation data, we can obtain the ionosphere-free combined observations, which will further improve the phase-smoothing-pseudorange performance of the TT-SD algorithm. The expansion of multi constellation is also an opportunity for Android devices to provide better GNSS positioning quality. For example, the above-mentioned Xiaomi 8 can support the acquisition of raw observations of GPS, GLONASS, Galileo, BeiDou and QZSS. When cycle slips or outliers occur in individual observations, the TT-SD filter with multi-GNSS can still provide robust filtering results because of the introduction of redundant observations without outliers. Therefore, in GNSS-adverse environments, such as urban canyons, where signals are disturbed, multi-GNSS will provide better positioning services for Android devices in terms of positioning availability and accuracy.

5. Conclusions

We analyzed the traditional phase-smoothed pseudorange method and its shortcomings towards GNSS observations on Android devices. Subsequently, we introduced three thresholds detection into the Hatch filter to adaptively adjust the smoothing window, for mitigating the impacts of the ionosphere cumulative errors, cycle slips, and gross errors. Meanwhile, we eliminated the receiver clock inconsistency between the pseudorange and the phase by the single difference between the satellites. An improved Hatch filter algorithm, i.e., the TT-SD Hatch filter algorithm has been proposed using only raw Android GNSS data without any external augmentation corrections. The ionosphere delay cumulative errors, cycle slips and outliers suppressed by the TT-SD Hatch filter algorithm were verified by experiments. To eliminate the effects of frequent smoothing window resets, we combined TT-SD Hatch filter and Kalman filter for status update and measurement update to achieve the smoothing positions. Finally, the feasibility of the method is verified by static and kinematic experiments using raw GNSS measurements from a Nexus 9 Android tablet, and the following conclusions are obtained.

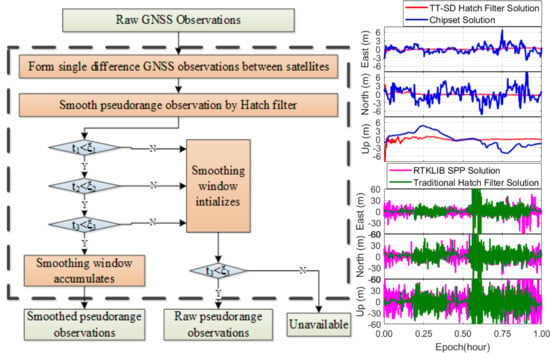
• The static experiment shows that the horizontal and vertical position errors of TT-SD Hatch filter solution are about 0.6 and 0.8 m in terms of RMS, respectively, after taking a few minutes to convergence. Conversely, the horizontal and vertical positioning errors of chipset solution are approximately 2.6 m and 2.5 m and vary with time. Both the SPP solution and the traditional Hatch filter solution have the position RMS exceed 10 m in horizontal and vertical components. Moreover, the smoothing effect of the traditional Hatch filter will fail when a large number of cycle-slips or gross errors in the observations appear. In contrast, the TT-SD Hatch filter can accurately detect the cycle slips and gross errors and reset the smoothed window in time, thus avoiding this problem. Meanwhile, with the aid of the Kalman filter, the TT-SD Hatch filter can achieve continuous positioning with steady accuracy.
• The kinematic experiment shows that the TT-SD Hatch filter solution can converge after a few minutes, and the 2D error is about 0.9 m, which is about 64%, 89% and 92% lower than that of the chip solution, the traditional Hatch filter solution and SPP solution, respectively. Meanwhile, the TT-SD Hatch filter solution can recover a continuous driving track but the solutions based on the other methods do not work. Moreover, traditional Hatch filter solution and SPP solution present higher-level measuring noise. However, we should note that the vehicle-borne experiment was carried out in an open and semi-open sky-view condition which cannot represent any GNSS-difficult environments. It is expected that our TT-SD Hatch filter solution will be degraded in such sorts of situations, not to mention the chipset solutions and traditional Hatch filter solutions.