1. Introduction
Earth observing satellite sensors data have played a crucial role in studies of the Earth’s surface and monitoring its changes. However, their data can only be used if they are well calibrated. Satellite sensor calibration is typically performed prior to launch and at selected periods throughout its mission lifetime after launch. Post-launch calibration can be performed in two distinct ways. First, using data from a National Institute of Standards and Technology (NIST)-traceable onboard source such as a solar diffuser or lamp system; Second, by use of a vicarious method performed through an analysis of images acquired over selected calibration targets. Since onboard calibrators are placed on the same sensor platform, they are also prone to the effects of harsh conditions in the space environment. Additionally, they can significantly add to the build and operating costs of the sensor mission. For these reasons, many satellite sensors (small-sats in particular) do not include on-board calibration support. Thus, external sources, such as image data acquired over Pseudo Invariant Calibration Sites (PICS), are used for satellite sensor calibration.
PICS are locations on the Earth surface which are homogeneous in nature and extremely stable over time. Many of these stable regions have been found throughout the Sahara Desert in North Africa [
1,
2,
3,
4,
5,
6,
7]. Some PICS are smaller in size, useful only for sensors possessing high spatial resolution. Many PICS, however, extend over regions of 100 km or more in size, making them useful for multiple sensors with low to moderate spatial resolution.
Chander et al. [
8] used Libya-4 for monitoring the on-orbit stability of Terra MODIS & Landsat-7 ETM+, and reported that their radiometric responses decreased less than 0.4% per year. Markham et al. [
9] used PICS to assess ETM+ stability and found similar results, estimating a change of less than 0.5% per year. In a separate analysis, Markham et al. [
10] assessed Landsat8 OLI stability using Libya-4, Libya-1, and Egypt-1 PICS data, and reported no observable changes in its response, to within the estimated uncertainty in the measurement procedure. Bhatt et al. [
11] studied calibration stability of the Visible Infrared Imaging Radiometer Suite (VIIRS) reflective solar bands using the Libya-4 desert. Their study found that the short period of VIIRS and target variability limited the minimum detectable trends to ±0.6%/yr for most visible bands, and ±2.5%/yr for short wave bands. Again, Wu et al. [
12] used Libya-4 to track the calibration performance of the VIIRS reflective solar bands, and estimated their stability to within 1%. Angal et al. [
13,
14] used images of the Sonoran desert to characterize Terra MODIS and ETM+ reflectance trends, and compared the results to the trend data derived from Libya-4. They found that the lifetime TOA reflectance’s for both sensors were changing no more than 0.1% per year in most bands (the exceptions were the ETM+ Blue band and MODIS Blue band).
Looking at traditional PICS, where sensor revisit patterns are limited (e.g., 16 days for Landsat sensors assuming consecutive cloud-free acquisitions) and, in some case, for short-term sensor mission lifetimes, there may be insufficient image data acquired over these sites to construct representative time series datasets, particularly during their early years of operation, when degradation tends to be the highest. In addition, smaller areas within an individual site may not truly be spatially stable, potentially resulting in false detection of drift in a sensor’s radiometric response.
Efforts have been made to extend the traditional PICS concept to include larger areas that allow for higher frequency imaging. Tabassum [
15] generated a list of 10 candidate invariant regions for each Landsat-8 OLI band, based on analysis of temporal and spatial uniformity across the continent of North Africa. Rather than specifically defined small rectangular regions of interest (ROIs), her regions were defined with respect to complex polygon boundaries forming contiguous areas representing “invariant” pixels. However, issues relating to the inclusion of “variant” pixels within an “invariant” region and/or exclusion of “invariant” pixels were not adequately addressed in her initial algorithm, and most of the identified regions were not common across all image bands. In addition, the question of potential imaging frequency was not addressed.
Vuppula [
16] presented a new technique known as the “PICS Normalization Process” (PNP) that combines OLI observations of multiple PICS into a single time series dataset with greater temporal resolution. She used the OLI data from six PICS (Libya-1, Libya-4, Sudan-1, Niger-1, Niger-2, and Egypt-1) and normalized them to Libya-4. The temporal resolution was increased to approximately 4 to 5 days compared to the 16 day OLI revisit time. Unfortunately, this combination method could not guarantee the generation of a dataset with daily or nearly daily acquisitions.
In their paper, Shrestha et al. [
17] wanted to identify “optimal” regions that were common across all image bands. They used an unsupervised classification technique to generate a set of 19 classes or “clusters” of spectrally similar OLI image pixels of North Africa based on cloud-free image data filtered for 5% or less temporal uniformity. Each of these clusters can be considered as an “extended” Pseudo Invariant Calibration Site (EPICS). One of the resulting clusters, Cluster 13, was found to possess a spectral response similar to Libya-4, and it contained a significant number of pixels forming relatively large contiguous regions across North Africa; this demonstrated great potential to ensure higher frequency imaging. However, their analysis required downsampling the image data to 300 m spatial resolution, and their results could not be validated with respect to the full resolution image data. In addition, potential BRDF effects were not addressed when generating the spatial and temporal statistics from original cluster data.
The main purpose of this analysis is to demonstrate the EPICS potential to detect sensor change quicker than traditional PICS via a more temporally rich dataset. Results of this study show that moderate resolution sensors, such as the Landsat 8 OLI, may acquire cloud-free images of Cluster 13 regions once every 1.4 days (using limited and cloud-free scenes only), in contrast to the 18–20 days on average cloud free revisit cycle found over a typical traditional PICS. Although EPICS provided significant improvements in the temporal density of the calibration time series, the resulting analysis showed that the Cluster 13 EPICS exhibited less than 3% uncertainty in its mean temporal TOA reflectance. Using the high density time series, it will be shown that the same period of OLI data over EPICS can provide lower statistically significant minimum detectable trends although Cluster 13 temporal uncertainty is typically found to have uncertainty values which are 1%~2% higher compared to traditional PICS.
Native Landsat 8 OLI, Landsat 7 ETM+, Sentinel 2A&B MSI image data were used to estimate the overall temporal and spatial variation in radiometric measurements over a major Cluster 13 sub-region (~40% of total area covered by Cluster 13 pixels). In addition, OLI data from Clusters 1, 3, 4, 16, and 19 were analyzed to evaluate sensors across their wider operating dynamic range.
The paper is presented as follows:
Section 1 provides a brief review of the topic and previous research performed in this area.
Section 2 describes the dataset, mask generation process and application approach in greater detail.
Section 3 presents produced results and critical analysis of the results when this process is applied to a number of different sensors. Finally,
Section 4 offers some concluding remarks.
4. Summary and Conclusions
This paper focuses on the application of EPICS (Cluster) for stability monitoring of optical satellite sensors. EPICS provides a significant improvement of the temporal revisit period of calibration time series in contrast to the temporal revisit period offered by traditional PICS with similar or 1%~2% higher temporal uncertainties depending on bands. One of the clusters, Cluster 13 (using limited regions and cloud-free scenes only), offers temporal revisit period of potentially as good as 1.4 days for Landsat 8 OLI in contrast to an average of every 18–20 days obtained from traditional PICS. By using all the regions of Cluster 13 and a nominal cloud consideration (~around 30% scene rejection due to cloud cover) a temporal revisit period of 0.33 day (~three cloud free collects everyday) can be obtained by a moderate resolution sensor. Furthermore, for the sensors having a wide field of view, Cluster 13 can offer even less than this revisit period. This improvement in the temporal revisit period resulted in better (depending on bands the increase in sensitivity as large as ~2 times) sensitivity of drift detection.
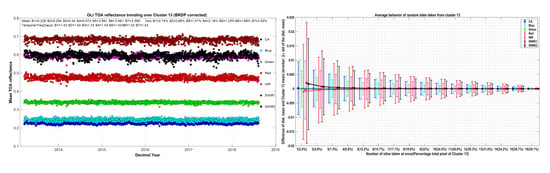
The temporal uncertainty of Cluster 13 was analyzed and validated using Landsat 8 OLI, Landsat 7 ETM+, Sentinel 2A MSI, and Sentinel 2B MSI. All sensors agree that Cluster 13 is temporally stable within 3%. However, spatial uncertainty of Cluster 13 is around 5% which is slightly more variation than that of traditional PICS. This extra spatial variation is pronounced due to its large spatial extent across the continent. Even though Cluster 13 with its hugely extended target size has spatial uncertainty of 5%, still the goal of matching traditional PICS temporal uncertainty is achieved. The near daily/daily calibration opportunity and increased sensitivity of change detection outweighs traditional PICS based methods, while also reducing the impact of a single location “change”.
This paper also suggests that a single random location from Cluster 13 can be a representative of the whole Cluster 13 with 2% uncertainty. This uncertainty value becomes smaller exponentially with the increase of chosen locations. A typical decrease of uncertainty values to 1% using only 3 sites has been observed while mean values estimated by 3 sites differs no more than 0.0439% of Cluster 13 mean TOA reflectance values. This suggests that the Cluster 13 mean TOA reflectance can be estimated within a specified uncertainty using fewer number of sites that is tunable to achieve desired accuracy.
The analysis in this work is more focused on Cluster 13 as it has better spatial uncertainty across all the bands and widely distributed across North Africa. But there are other clusters, such as Cluster 1, 3, 4, 16, and 19, which have spatial uncertainty and distribution across North Africa comparable with Cluster 13. Initial results showed that these clusters also offer nearly daily acquisition as Cluster 13. These clusters possess a similar potential to be used for EPICS based sensor calibration within their specified uncertainty. The darkest of the found clusters, Cluster 4 has temporal TOA reflectance mean values ranging from 0.177–0.380 with absolute standard deviation values ranging from 0.011~0.0016. This generates temporal uncertainty values ranging from 5%~8% which are the highest values among the considered clusters and can be useful for calibration purposes considering the intensity level of this cluster. Furthermore, these clusters have different intensity levels which can help to perform radiometric calibration and stability monitoring of any satellite sensors in a wider dynamic range.
This paper showed that EPICS allows daily or near daily calibration and stability monitoring. EPICS offers up to two times (this number varies from band to band) better sensitivity in drift estimation than traditional PICS even with its continental extent. The proposed technique can be powerful for evaluating sensor performance in less time, especially for sensors with shorter lifespans and limited spatial coverage. Surprisingly, EPICS achieves all this improvement while offering less than 3% temporal variability in its reflectance time series.