The Summertime Diurnal Cycle of Precipitation Derived from IMERG
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Methodology
3. Results
3.1. Case Studies of the Diurnal Cycle of Precipitation
3.2. IMERG Summertime Climatology
3.3. The Amplitude and Phase of the Summertime Diurnal Cycle
3.4. Fitting Errors on the Amplitude and Phase of the Summertime Diurnal Cycle
3.5. Variations in the Diurnal Cycle of Accumulation across the Seasons
4. Discussion
- As previously suggested [3,4,14], the diurnal cycles of occurrence and accumulation are largely captured by the 24 h harmonic over land, though the 12 h harmonic is comparable in contribution with the 24 h harmonic over the ocean (Figure 4a,c and Figure 6a,c). A novelty of this study is that the 24 h and 12 h amplitudes for intensity are found to contribute comparably over most regions, with the superposition of the two harmonics leading to enhanced and muted peaks in the diurnal cycle (e.g., Figure 1b,c).
- As previously found [14], occurrence is clearly the main driver of the diurnal cycle of accumulation, as opposed to intensity. This is supported in this study by a strong correlation between occurrence and accumulation (Figure 3a,c), as well as coincidence of the regions where the 24 h amplitudes are pronounced (Figure 4a and Figure 6a) and similar phases of the 24 h harmonic peaks (Figure 4c and Figure 6c) corroborate this strong relationship.
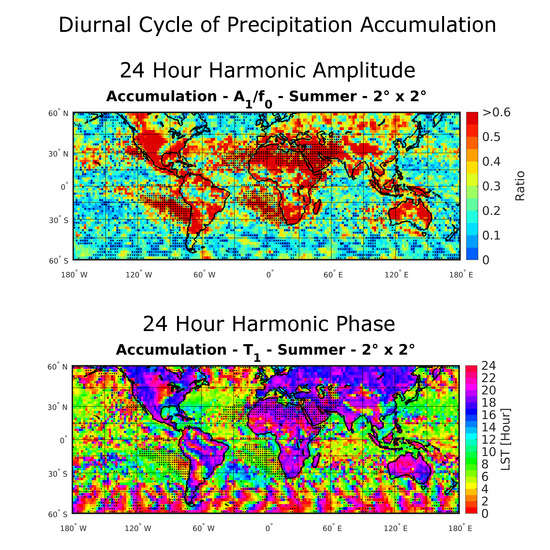
- The 24 h harmonic is the main contributor to the diurnal cycle of accumulation with large amplitudes (mostly > 25%) over land, peaking in the late afternoon and evening (Figure 6). Furthermore, 24 h amplitudes over ocean are again shown to be smaller (mostly < 25%) with mostly morning peaks as previously found [2,14], though some early afternoon peaks in the coastal regions should be noted.
- Large disagreements between the peak time of the 12 h harmonic for accumulation north of 30 have been identified between IMERG and a selection of other satellite precipitation products (TRMM TMPA, CMORPH, PERSIANN). Whilst TRMM TMPA and PERSIANN tend to maximise at ~3–7 LST and 15–19 LST and CMORPH tends to maximise at ~5–8 LST and 17–20 LST (see Figure 6 of [14]), IMERG tends to maximise at ~21–1 LST and 9–13 LST (Figure 6d). Errors on the IMERG phases exceeding 1 h can be found in such regions and may explain some of the discrepancies.
- When comparing the diurnal harmonic of accumulation between IMERG and TRMM TMPA, it is clear that the IMERG amplitude is much larger (~30–60%, Figure 6a) than the corresponding TRMM amplitude (~20–40%, see Figure 5j of [14]) over the North Atlantic and Pacific Oceans. Small errors in the IMERG amplitudes in these regions do not appear to explain such differences.
5. Conclusions
- The diurnal cycles of occurrence and accumulation over land are mainly contributed to by the 24 h harmonic, which tends to peak across late afternoon and evening (~16–24 LST), compared to the 12 h harmonic, which tends to peak in the early to mid morning and early afternoon to early evening (~2–8 LST and 14–20 LST) (Figure 4 and Figure 6). However over ocean, the contributions are comparable for the 12 h harmonic, which tends to peak between late evening to early morning and late morning to early afternoon outside of the convergence zones (~21–2 LST and 9–14 LST), and the 24 h harmonic, which peaks in the morning in open regions (~0–10 LST) and between late morning and afternoon in the coastal regions (~8–15 LST). The diurnal cycle of intensity is similarly contributed to by the 24 h harmonic, which typically peaks between mid evening and early morning (~20–4 LST) over land ( N–S) and early to late morning (~3–12 LST) over ocean, and the 12 h harmonic, which peaks in the mid morning and the early evening (~5–8 LST and 17–20 LST) everywhere (Figure 5).
- The diurnal cycle of occurrence dictates the diurnal cycle of accumulation as opposed to intensity. This is supported by strong correlations in diurnal means between occurrence and accumulation (Figure 3a,c), in increased amplitudes in the 24 h harmonic regions (Figure 4a and Figure 6a), and in the time at which the 24 h harmonic peaks (Figure 4c and Figure 6c).
- Fitting errors on the 24 h and 12 h harmonics representing the diurnal cycle suggest that results over land are generally more reliable than over ocean, phases are generally more reliable than amplitudes, and that results for accumulation are generally more reliable than for occurrence and intensity (Figure 7). In particular, amplitudes and phases for occurrence and intensity should be treated with caution (except for the 24 h harmonic for occurrence over land). Furthermore, amplitudes and phases for accumulation in the 45–60N/S region should be treated with caution.
- The use of 24 h and 12 h harmonics is not sufficient to capture the diurnal cycle of intensity (see the distribution of black dots in Figure 5). Low correlations between the harmonic function and the diurnal cycle derived from IMERG data and/or high error estimates for most of the globe suggest that higher-order harmonics are required to better capture the diurnal cycle of intensity.
- IMERG precipitation estimates in the –S region present some anomalies, and results from these regions should be treated cautiously. This is specifically marked by pronounced precipitation occurrences, intensities and accumulations in this zonal region of the Pacific Ocean compared to the Indian and Atlantic Oceans (Figure 3). These artifacts are under investigation.
- Variations in the diurnal cycle of accumulation across the seasons are minimal in the tropics, where diurnal amplitudes are stronger (mostly exceeding 60% over land) throughout the seasons, and more evident in the mid-latitudes (Figure 8). Summertime mid-latitude diurnal amplitudes tend to exceed those in winter. The diurnal cycle of accumulation tends to maximise at similar times across all seasons over land, whilst more variations are found over the mid-latitude oceans.
- The summertime diurnal cycle of precipitation was unaffected by the strong El Nino event of 2015/2016. This suggests that four years of IMERG data are sufficient for analysing the diurnal cycle of precipitation at resolution.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CMORPH | Climate Prediction Center morphing |
| CORRA | Combined Radar-Radiometer |
| DPR | Dual-frequency Precipitation Radar |
| GMI | GPM Microwave Imager |
| GPM-CO | Global Precipitation Measurement Mission Core Observatory |
| GPROF | Goddard Profiling Algorithm |
| IMERG | Integrated Multi-satellitE Retrievals for GPM |
| ITCZ | Intertropical Convergence Zone |
| JAXA | Japan Aerospace Exploration Agency |
| LST | Local Solar Time |
| NASA | National Aeronautics and Space Administration |
| PERSIANN | Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks |
| PMW | Passive Microwave |
| SPCZ | South Pacific Convergence Zone |
| TMPA | Tropical Rainfall Measuring Mission Multi-satellite Precipitation Analysis |
| TRMM | Tropical Rainfall Measuring Mission |
| US | United States |
| UTC | Coordinated Universal Time |
References
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The changing character of precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–1218. [Google Scholar] [CrossRef]
- Covey, C.; Gleckler, P.J.; Doutriaux, C.; Williams, D.N.; Dai, A.; Fasullo, J.; Trenberth, K.; Berg, A. Metrics for the diurnal cycle of precipitation: Toward routine benchmarks for climate models. J. Clim. 2016, 29, 4461–4471. [Google Scholar] [CrossRef]
- Wallace, J.M. Diurnal variations in precipitation and thunderstorm frequency over the conterminous United States. Mon. Weather Rev. 1975, 103, 406–419. [Google Scholar] [CrossRef]
- Dai, A. Global precipitation and thunderstorm frequencies. Part II: Diurnal variations. J. Clim. 2001, 14, 1112–1128. [Google Scholar] [CrossRef]
- Xiao, C.; Yuan, W.; Yu, R. Diurnal cycle of rainfall in amount, frequency, intensity, duration, and the seasonality over the UK. Int. J. Climatol. 2018, 38, 4967–4978. [Google Scholar] [CrossRef]
- Negri, A.J.; Bell, T.L.; Xu, L. Sampling of the diurnal cycle of precipitation using TRMM. J. Atmos. Ocean. Technol. 2002, 19, 1333–1344. [Google Scholar] [CrossRef]
- Nesbitt, S.W.; Zipser, E.J. The diurnal cycle of rainfall and convective intensity according to three years of TRMM measurements. J. Clim. 2003, 16, 1456–1475. [Google Scholar] [CrossRef]
- Liu, C.; Zipser, E.J. Diurnal cycles of precipitation, clouds, and lightning in the tropics from 9 years of TRMM observations. Geophys. Res. Lett. 2008, 35, L04819. [Google Scholar] [CrossRef]
- Huffman, G.J. The Transition in Multi-Satellite Products from TRMM to GPM (TMPA to IMERG). Technical Report. NASA. 2018. Available online: https://pmm.nasa.gov/sites/default/files/document_files/TMPA-to-IMERG_transition_180827.pdf (accessed on 3 June 2019).
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-SatellitE Retrievals for GPM (IMERG). Algorithm Theoretical Basis Document, Version 5.2; 2018; p. 35. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V5.2_0.pdf (accessed on 18 June 2019).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Bowman, K.P.; Fowler, M.D. The diurnal cycle of precipitation in tropical cyclones. J. Clim. 2015, 28, 5325–5334. [Google Scholar] [CrossRef]
- Dai, A.; Lin, X.; Hsu, K.L. The frequency, intensity, and diurnal cycle of precipitation in surface and satellite observations over low-and mid-latitudes. Clim. Dyn. 2007, 29, 727–744. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (GPM) Mission for Science and Society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Kirschbaum, D.; Petersen, W.; Huffman, G.; Kidd, C.; Stocker, E.; Kakar, R. The Global Precipitation Measurement (GPM) mission’s scientific achievements and societal contributions: Reviewing four years of advanced rain and snow observations. Q. J. R. Meteorol. Soc. 2018, 144, 27–48. [Google Scholar] [CrossRef] [PubMed]
- Sungmin, O.; Kirstetter, P. Evaluation of diurnal variation of GPM IMERG-derived summer precipitation over the contiguous US using MRMS data. Q. J. R. Meteorol. Soc. 2018, 144, 270–281. [Google Scholar] [CrossRef]
- Dezfuli, A.K.; Ichoku, C.M.; Huffman, G.J.; Mohr, K.I.; Selker, J.S.; Van De Giesen, N.; Hochreutener, R.; Annor, F.O. Validation of IMERG precipitation in Africa. J. Hydrometeorol. 2017, 18, 2817–2825. [Google Scholar] [CrossRef]
- Dai, A.; Giorgi, F.; Trenberth, K.E. Observed and model-simulated diurnal cycles of precipitation over the contiguous United States. J. Geophys. Res. Atmos. 1999, 104, 6377–6402. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Tokay, A. A novel approach to identify sources of errors in IMERG for GPM ground validation. J. Hydrometeorol. 2016, 17, 2477–2491. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Kirstetter, P.E.; Tian, Y. Performance of IMERG as a function of spatiotemporal scale. J. Hydrometeorol. 2017, 18, 307–319. [Google Scholar] [CrossRef]
- Joyce, R.J.; Xie, P. Kalman filter–based CMORPH. J. Hydrometeorol. 2011, 12, 1547–1563. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.L.; Sorooshian, S.; Gao, X. Precipitation estimation from remotely sensed imagery using an artificial neural network cloud classification system. J. Appl. Meteorol. 2004, 43, 1834–1853. [Google Scholar] [CrossRef]
- NASA. IMERG 3B-HHR, Version 5 (V05). NASA’s Precipitation Processing System. Subset Used: June 2014–May 2018. 2018. Available online: ftp://arthurhou.pps.eosdis.nasa.gov (accessed on 23 September 2018).
- NASA. Global Precipitation Measurement Precipitation Processing System. File Specification. 3IMERGHH. Preliminary Version. 2017. Available online: https://storm.pps.eosdis.nasa.gov/storm/data/docs/filespec.GPM.V1.3IMERGHH.pdf (accessed on 11 March 2019).
- Huffman, G.J. Estimates of root-mean-square random error for finite samples of estimated precipitation. J. Appl. Meteorol. 1997, 36, 1191–1201. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Integrated Multi-satellitE Retrievals for GPM (IMERG) Technical Documentation. Technical Report. NASA. 2017. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_doc.pdf (accessed on 10 July 2019).
- Battaglia, A.; Mroz, K.; Watters, D.; Ardhuin, F. GPM-derived climatology of attenuation due to clouds and precipitation at Ka-band. IEEE Trans. Geosci. Remote Sens. Conditionally accepted.








© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watters, D.; Battaglia, A. The Summertime Diurnal Cycle of Precipitation Derived from IMERG. Remote Sens. 2019, 11, 1781. https://doi.org/10.3390/rs11151781
Watters D, Battaglia A. The Summertime Diurnal Cycle of Precipitation Derived from IMERG. Remote Sensing. 2019; 11(15):1781. https://doi.org/10.3390/rs11151781
Chicago/Turabian StyleWatters, Daniel, and Alessandro Battaglia. 2019. "The Summertime Diurnal Cycle of Precipitation Derived from IMERG" Remote Sensing 11, no. 15: 1781. https://doi.org/10.3390/rs11151781
APA StyleWatters, D., & Battaglia, A. (2019). The Summertime Diurnal Cycle of Precipitation Derived from IMERG. Remote Sensing, 11(15), 1781. https://doi.org/10.3390/rs11151781