Object-Based Flood Analysis Using a Graph-Based Representation

Abstract

The amount of freely available satellite data is growing rapidly as a result of Earth observation programmes, such as Copernicus, an initiative of the European Space Agency. Analysing these huge amounts of geospatial data and extracting useful information is an ongoing pursuit. This paper presents an alternative method for flood detection based on the description of spatio-temporal dynamics in satellite image time series (SITS). Since synthetic aperture radar (SAR) satellite data has the capability of capturing images day and night, irrespective of weather conditions, it is the preferred tool for flood mapping from space. An object-based approach can limit the necessary computer power and computation time, while a graph-based approach allows for a comprehensible interpretation of dynamics. This method proves to be a useful tool to gain insight in a flood event. Graph representation helps to identify and locate entities within the study site and describe their evolution throughout the time series.

1. Introduction

Increasing amounts of satellite data are available for monitoring spatial phenomena on the Earth’s surface. Radar sensors are, unlike optical sensors, practically unaffected by weather conditions or daytime, and can therefore be used to detect water bodies in rainy circumstances. A lot of research is being done on single date radar image analysis (flood delineations, classifications, etc.) or bi-temporal change detection (image differencing, post-classification comparison, etc.) [1,2,3,4,5,6,7,8,9,10]. However, increasing quantities of geospatial data demand a different approach of analysis. In the current big data environment, data veracity, volume, accessibility, and the rate of change imposes new approaches to understand, analyse, consume, and visualise geospatial data solutions [11].

Satellite image time series (SITS) are collections of satellite images that consider the same spatial extent on different timesteps. Data mining tools for SITS, based on object-based image analysis (OBIA), are currently confined to a few authors [1,12,13]. Guttler et al. [12] created a methodological framework to automatically detect and extract spatio-temporal information from SITS. They combine an OBIA with a graph-based representation. Khiali et al. [13] developed this approach further with an object-clustering goal to obtain a supervised classification. Their approach is restricted to the visible spectrum, treating a multi-class spatio-temporal analysis.

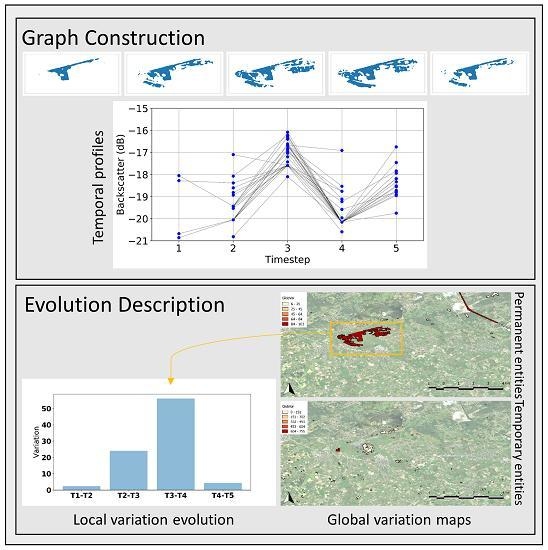
This paper explores the applicability of combining OBIA with a graph-based representation on synthetic aperture radar (SAR) data for single class spatio-temporal analysis.

2. Data

2.1. Study Area

2.1.1. Geographical Location

Schulensbroek is a nature reserve in north-eastern Belgium, located within the water catchment area of the river Demer. Other waterways, namely the Herk, the Velpe, the Gete, and the Mangelbeek merge here in the Demer. Since the 1970s, the nature reserve has functioned as a flood control area (FCA), which consists of 95 ha permanent basin, the Schulensmeer, and a surrounding area of 190 ha with natural borders. The current water management, including the flooding regime, is largely artificial. During peak discharge, the Demer water is actively pumped into the Schulensmeer. Emptying is done gravitationally.

For the purpose of this research, two regions of interest are delimited within the study area, i.e., the dynamic zone and the static zone (Figure 1). The FCA Schulensmeer/Schulensbroek is located in the ’dynamic zone’, and this zone is expected to display high dynamics during a flood event. As a reference, the dynamics of Schulensbroek will be compared to the dynamics of a part of the Albert Canal, situated within the ’static zone’ on Figure 1. The static zone is expected to display low dynamics.

2.1.2. Flood Event

During the end of May and the beginning of June 2016, large amounts of precipitation led to the flooding of the FCA on 7 June 2016. The closest available weather information was found in a weather station in Alken [14], which is located at 15 km from Schulensbroek. Daily precipitation measured in this station is depicted in Figure 2. Other information from this weather station, such as mean and maximum wind speed, can be used for interpretation of the results (Section 2.3).

2.2. Satellite Imagery

Sentinel-1, part of ESA’s Copernicus project, is an imaging radar mission providing continuous all-weather, day-and-night imagery at C-band (4 to 8 GHz wavelength). These properties allow the Sentinel-1 products to be used for flood monitoring [15]. Depending on the size and location of the study area, the Sentinel-1 mission can provide a temporal resolution of three to six days. The data used for this research is Level-1 Ground Range Detected (GRD), which consists of focused SAR data that has been detected, multi-looked and projected to ground range using an Earth ellipsoid model [16]. Pixel values represent detected amplitude, while phase information is lost. The spatial resolution of the data amounts to 10 m × 10 m.

Because of different viewing directions, comparing imagery captured during an ascending orbit with imagery captured during a descending orbit can result in geometric distortions caused by foreshortening and layover [15]. For this reason, the imagery is processed separately depending on its capture direction. Capture dates in the period of the flood are listed in

Table 1. Available Sentinel-1 Ground Range Detected (GRD) imagery before, during, and after the flood event of 7 June 2016.

Date	Cycle Number	Orbit Number	Relative Orbit	Pass Direction	Timestep
26 May 2016 T17:32:36.879Z	79	11433	161	ASCENDING	1
2 June 2016 T17:24:20.972Z	80	11535	88	ASCENDING	2
7 June 2016 T17:32:30.230Z	80	11608	161	ASCENDING	3
14 June 2016 T17:24:21.752Z	81	11710	88	ASCENDING	4
1 July 2016 T17:32:31.635Z	82	11958	161	ASCENDING	5
23 May 2016 T05:58:14.315Z	79	11382	110	DESCENDING	1
30 May 2016 T05:50:02.415Z	80	11484	37	DESCENDING	2
4 June 2016 T05:58:25.425Z	80	11557	110	DESCENDING	3
11 June 2016 T05:50:03.148Z	81	11659	37	DESCENDING	4
16 June 2016 T05:58:26.140Z	81	11732	110	DESCENDING	5
28 June 2016 T05:58:26.823Z	82	11907	110	DESCENDING	6
5 July 2016 T05:50:04.559Z	82	12009	37	DESCENDING	7

[17].

2.3. Contextual Data

In order to interpret the results, extra information on the prevailing weather conditions at the time of satellite image capture were gathered from the Alken weather station [14]. This data holds information on maximum and mean wind speed and precipitation amounts during satellite image capture. These factors can significantly influence the backscatter of water bodies in radar imagery. Smooth water surfaces usually appear black in SAR imagery due to the specular reflection, while wind-ruffled water surfaces can induce large backscatter signals, complicating the detection of water surfaces on SAR images [18].

3. Method

In this paper, we propose an exploratory data mining approach based on the technique of Guttler et al. [12], with a focus on the evolution of water bodies during a flood event. While the research of Guttler et al. [12] focuses on analysis in the visible spectrum, the current paper explores the possibilities of this object-based graph representation for SAR imagery. Moreover, this research, focuses on a binary problem, i.e., evolution of water/non-water surface area, with no need for classification. After preprocessing the SAR data (Section 3.1), object delineation is done by an active contour model (Section 3.2) and object characterisation is based purely on radar backscatter. Objects are then grouped in graphs according to their spatio-temporal overlap, and resulting evolution graphs summarize the temporal profiles of the extracted spatio-temporal phenomena (Section 3.3 and Figure 3). The temporal profiles can be used to synthesize entity evolution and temporal behaviours. This approach allows to delineate zones of high spatio-temporal dynamics and to quantify these dynamics.

3.1. Preprocessing

The Sentinel Application Platform (SNAP), containing all Sentinel Toolboxes, is used for the preprocessing of the GRD data, obtained from SentinelHub (see Figure 4) [17,19]. This section describes the preprocessing steps depicted in Figure 4.

The orbit file, providing accurate satellite position and velocity information, is applied on the GRD data. Based on this information, the orbit state vectors in the abstract metadata of the product are updated. Thereafter thermal noise removal is executed following a noise look-up table (LUT) file which exists for each Sentinel-1 Level-1 data set. The values in the de-noise LUT, provided in linear power, can be used to derive calibrated noise profiles matching the calibrated GRD data. Calibration is the next step in the preprocessing, converting digital pixel values to radiometrically calibrated backscatter in order to provide imagery in which the pixel values are directly related to the radar backscatter of the scene. For most applications, applying the same calibration type to all of the data (Sigma-0, Beta-0, Gamma-0) is more important than the selected calibration type itself [20]. Small [20] suggests that the Gamma-0 signal is less influenced by the incidence angle (and thus by the orbit) than Sigma-0. In that regard, we opted to calibrate the data to the Gamma-0 signal. Considering the polarisation factor, both co-polarised data (VV) and cross-polarised data (VH) have the potential for classification errors. Because VH produces a wider range of backscatter values from vegetated land surfaces compared to VV, low backscatter values of land surface can be confused with the low backscatter values associated with water [15,18], leading to misclassification of land as flood. Twele et al. [15] concluded that the VV polarisation provides a slight advantage for flood delineation, yet this polarisation in more susceptible to roughening of the water surface caused by rain or wind [18]. In this research, both VV and VH signals were processed and respective results are compared.

Due to topographical variations of a scene and the tilt of the satellite sensor, distances can be distorted in the SAR images. Range Doppler Terrain Corrections are intended to compensate for these distortions so that the geometric representation of the image will be as close as possible to the real world. In order to establish a correct pixel mapping between the different rasters, a stack is created. The geographical position of a master sample is used to find the corresponding sample in the slave raster. The collocation algorithm requires accurate geopositioning information for both master and slave products. In this way, pixel values are resampled into the same geographical raster. A spatial subset is obtained based on the geographical coordinates of the region of interest. And finally, a speckle filter is applied, because SAR images display a speckled texturing which impedes interpretation of features. For this research the ’refined Lee filter’ is chosen, which is a minimum mean square error (MMSE) filter, based on the multiplicative noise model [21]. The refined Lee Filter is an adaptive filter and such a type of filter is required in order to maintain the edges in the scene [22]. This filter shows an improved performance when compared with the original Lee filter, and moreover, it requires a minimum of input parameters compared to other filters [23].

3.2. Active Contour Model Segmentation

Delineating floods in SAR imagery is a much studied research topic and different approaches have been developed over the years [6,24,25,26,27,28,29,30]. For this research, different approaches were tested for finding an optimal delineation of water bodies in the radar images, namely ’Minimum error thresholding’ by Kittler and Illingworth [25], ’Threshold Selection Method from Gray-Level Histograms’ by Otsu [30], and ’Tiled Thresholding’ by Martinis et al. [31]. However, none of the aforementioned methods resulted in a robust segmentation over the different timesteps, leading to enormous over- or underestimations of the present surface water.

Landuyt et al. [32] compared available SAR-based flood mapping algorithms and concluded that active contour models (ACM) are suited for flood mapping in smaller regions. ACM is a framework in computer vision which groups pixels from preprocessed raster images into objects [33]. It produces, to a certain extent, consistent results, and it requires little parameters and postprocessing. This allows for a fast classification of present surface water leading to a fast segmentation. The model is based on an energy minimization problem, defined by weighted values corresponding to the sum of differences from the average backscatter values outside the segmented region, the sum of differences from the average backscatter values inside the segmented region, and a term which is dependent on boundary length of the segmented region [27].

The ACM requires an initial contour position [33]. For this research, the backscatter of water pixels is expected to be much lower then of non-water pixels, due to the specular effect. The 5% ’darkest’ pixels, i.e., with the lowest backscatter, are chosen as seeds to initialize the contours for the ACM. This amount of seed pixels was chosen by trial and error, as were the other parameters: smoothing factor $\mu$ equals 0.99 for ill-defined contours, ${\lambda }_1>{\lambda }_2$ for quite uniform water bodies and varying backscatter outside the water bodies, and the maximum number of iterations is set to 200.

3.3. Graph Representation

Guttler et al. [12] proposed a methodology to track entity evolutions in a time series of satellite images. Their research, however, is developed in order to make a supervised classification of different land use classes. In order to obtain this goal, they introduce the concept of reference objects, which are described by other objects in the time series. Since this research focuses on a binary problem (i.e., water/non-water), the use of reference objects becomes superfluous. Objects are defined as detected water polygons at each image capture date. The capture dates form the timesteps of the time series. Objects (polygons) are then grouped into entities (water bodies) according to their spatial overlap. For each entity a graph is built representing the spatio-temporal overlap of this selection of polygons over the time series. This paper implements a refined version of the methodology as described by Khiali et al. [13]. The entities to be monitored are water bodies as detected by the active contour modelling on SAR imagery (Figure 3).

The evolution of each entity is described by means of a selection of polygons in the time series. A Directed Acyclic Graph (DAG), $G_0*=(V_0*,E_0*)$, is built for each entity where the nodes represent polygons which are classified as water bodies by the ACM, and the edges represent their spatio-temporal overlap (Equations (1) and (2) from Khiali et al. [13]).

$$V_0*=\left\{o|oϵ\vartheta ,|Pix(o*)\cap Pix\left(o\right)|\ge 0\right\}.$$

(1)

$$E_0*=\left\{(o^i,o^j)|o^iϵO_t\cap V_o*,o^jϵO_{t+1}\cap V_o*andPix\left(o^i\right)\cap Pix\left(o^j\right)\ne \mathsf{⌀}\right\}.$$

(2)

According to Equations (1) and (2), polygons are grouped in an entity if they display a spatial overlap, and edges are created between overlapping polygons of consecutive timesteps. In this way, each entity $o*$ is described by an evolution graph $G_o*$. The graph can be organized by layers where each layer corresponds to a timestep from the SITS. If radiometric information, i.e., mean backscatter values, is represented on a second axis, a temporal profile is obtained.

Visual inspection of temporal profiles gives an idea of the homogeneity and dynamics of the entity. While backscatter values are also dependent of incidence angle (or orbit) and prevailing weather conditions, these values give an indication on dynamics within the entity. In order to quantify these dynamics within each graph, the variation ($Var$) between two consecutive timesteps is calculated as follows (Equation (3)) [12] :

$$Var(G_i,G_{i+1})=\sum _{o_j\in G_i}^{}{\displaystyle \frac{size\left(o_j\right)}{size\left(G_i\right)}}.{\displaystyle \frac{{\sum }_{o_k\in G_{i+1}}{w}_{j,k}.dist(o_j,o_k)}{{\sum }_k{w}_{j,k}}}.$$

(3)

Equation (3) describes the variation within one entity (graph) between timestep i and timestep $i+1$ as the weighted sum of variations of all polygons at timestep i, where as these polygon variations are defined by the difference in backscatter with overlapping polygons from the next timestep ($i+1$), weighted by their amount of spatial overlap.

The global variation ($GlobalVar$) for a graph represents the sum of the variations on each timestep (Equation (4)). The value of $GlobVar$ reflects the temporal behaviour of the entity, where high values indicate high spatio-temporal dynamics.

$$GlobalVar\left(G\right)=\sum _{i=1}^{n-1}Var(G_i,G_{i+1}).$$

(4)

Processing the spatio-temporal data in graphs results in evolution graphs, temporal profiles and global variation maps. The evolution graphs describe the spatial evolution of the entities. The graphs indicate which polygons overlap with each other on consecutive timesteps. Connected polygons are assumed to form a spatio-temporal entity, in this case, a water body. Temporal profiles are composed by adding radiometric information to the evolution graphs. The evolution graph is placed in a 2-dimensional plane, where the x-axis represents the timestep on which the radar image was captured, and the y-axis shows mean backscatter of the polygon which the node represents. Temporal profiles can depict any object attribute for the nodes in a given graph. For this research, the mean backscatter attribute is displayed in the temporal profiles.

Within each temporal profile, variation to the next timestep is calculated according to Equation (3). For the whole study area, global variation is calculated with Equation (4). Plotting these global variation values for each entity yields a global variation map for the whole study site.

4. Results

All calculations were processed on Intel(R) Core(TM) i7-4770 CPU @ 340GHz with 16.0 GB of RAM. The time necessary for running through all steps in the methodology amounted to up to 45 min for the longest time series (7 timesteps). Preprocessing was done with SNAP GUI. The remaining part of the workflow was programmed in Python.

The computation time is mostly dependent of the total number of polygons involved in each time series, ranging from 423 polygons in the descending SITS with VH polarisation to 745 polygons in the descending time series with VV polarisation.

In order to evaluate the proposed framework, firstly the results for the entire study site were interpreted. Thereafter, the dynamics at a local scale were evaluated and analysed.

4.1. Global/Study Site Level

Comparing the segmentation results for the different signals for the whole study site (Figure 5), the VH signal appears to result in a higher overall estimation of the water area. Since the capture dates differ for the ascending and the descending SITS, the flood peak appears to be shifted between the different SITS, yet a comparable flood evolution manifests itself.

After aggregating the polygons according to their spatial overlap with other polygons on consecutive timesteps, three types of graphs arise. Full graphs, spanning all timesteps, are obtained for permanent entities, i.e., they exist from the first timestep throughout the whole time series to the last timestep. Incomplete graphs represent temporary entities. They exist for a part of the time series (at least two timesteps). Finally, unconnected polygons form one-node graphs, because they have no spatial overlap with other polygons on the previous or following timestep.

In Figure 6 we compare the distribution of these different entities over the time series for the different signals. High amounts of unconnected polygons indicate unstable boundaries of the graph objects and can be related to high dynamics. However, this behaviour might as well be the result of an unstable segmentation [12], thus the amount of disconnected polygons can be employed as an indicator to estimate the quality of the time series segmentation.

Temporary entities can be expected around the flood peak (timestep 3 for the ascending SITS and timestep 4 for the descending SITS, see also Table 1). If they occur at another point in the time series, this might as well be an indication of unstable segmentation. Figure 6 shows that the signals with VV polarisation result in higher areas of unconnected polygons and temporary entities, which leads us to believe these segmentations are less stable than for the SITS with VH polarisation.

The global temporal profiles, showing the evolution graphs of the entire study site, are depicted in Figure 7 and Figure 8. Colour codes indicate the type of entity the nodes (polygons) belong to, x-values indicate the timestep on which the node (polygon) exists and y-values represent backscatter values. Generally, permanent entities (blue nodes in Figure 7 and Figure 8) display a lower mean backscatter, while unconnected polygons (red nodes) display a higher mean backscatter. Global backscatter variation is induced by varying weather conditions and differing orbits (e.g., timestep 2 versus timestep 3 in Figure 7).

Global variation values are calculated for each graph (Equation (4)), and thus for each entity. For variation values to be calculated, the water bodies should be present for least two consecutive timesteps. No variation can be calculated for unconnected polygons because variation is a function of the spatio-temporal overlap. The dynamics of these objects is too high to describe its variation. These objects are comparable with objects that only exist in between two timesteps, these objects will not be detected and hence no variation values will be calculated.

The other categories, i.e., permanent entities and temporary entities, are treated separately because the magnitude of variation depends on the number of timesteps involved. Global variation is mapped for permanent entities in Figure 9 and for temporary entities in Figure 10 (different scales!). For permanent water bodies, the canal in the static zone displays a high $GlobVar$ when captured by the VV signals. This is unexpected and possible explanations are treated in the discussion section. Moreover, part of the flood in the dynamic zone is for some signals described by the permanent entity, while the same area is part of a temporary entity for other signals, e.g., descending VV versus descending VH (Figure 9).

Table 2. Number of polygons in the SITS and global variation for the whole study area and regions of interest.

	Number of Polygons		GlobVar
		Study Area	Dynamic Zone	Static Zone
Ascending VV	568	1582.92	103.61	86.67
Ascending VH	434	350.62	72.39	19.00
Descending VV	745	1260.16	54.07	194.83
Descending VH	423	987.85	309.54	106.53

presents the global variation values for the whole study area, the dynamic zone and flood zone. Because the descending time series cover more timesteps than the ascending time series (7 versus 5), higher $GlobVar$ values are expected for the descending time series since $GlobVar$ is calculated as the sum of variations to the consecutive timesteps. Moreover, higher $GlobVar$ values are expected for the dynamic zone in comparison with the static zone. The total number of polygons in the SITS, which is a result of the ACM, is also displayed in Table 2.

4.2. Local/ Graph Level

Two subregions are selected within the study site (Figure 1). The first region, the ’Static zone’ contains the Albert Canal, which is assumed to maintain static surface area throughout the flood event. The second region, the ’Dynamic zone’ contains the FCA and is assumed to display high dynamics during the flood event. Segmentation results and the evolution of variation are examined separately for the static zone and the dynamic zone.

4.2.1. Static Zone: Canal

Ascending SITS

ACM segmentation results for the static zone are depicted in Figure 11 for the ascending time series. The canal is, for both VV and VH polarisations, captured by two permanent entities (two full graphs), separated by a bridge in the south east of the static zone (Figure 12). The associated temporal profiles and variation of the biggest entity within the static zone are shown in Figure 13. The canal is highly fragmented on timestep 3 in the VV SITS and on timestep 2 in the VH SITS (Figure 11). This fragmentation can be observed in the temporal profile and is reflected in the variation, i.e., a high variation is displayed on the transition from highly fragmented entities to barely fragmented entities (see variation peaks in Figure 13).

Descending SITS

Segmentation results for the descending time series in the static zone are depicted in Figure 14. The associated temporal profiles and variation are shown in Figure 15. A fragmentation of the canal is observed on timesteps 1–3 for the VV time series, and on time step 3 for the VH time series. However on timestep 7 in the VV time series, the ACM fails to split up the canal at the bridge in the south east of the static zone (Figure 14). As a consequence, the VV SITS results in only one permanent entity for the canal, which, in combination with high fragmentation in the beginning of the time series, results in high variation values (Figure 15). For the VH SITS, the canal is split up into two permanent entities because of the presence of the bridge in the south east of the static zone (similar to the result of the ascending SITS, discussed before in Figure 12).

4.2.2. Dynamic Zone: FCA

Ascending SITS

The dynamic zone, i.e., the region that contains the FCA, exhibits a different behaviour. As mentioned in the global results section (Section 4.1), the flood area is not always captured within one graph or entity. The dynamic zone is characterized by the occurrence of temporary entities. For instance, on timesteps 2–5 in Figure 16, a significant water area is not included in the permanent entity for the VV SITS while it is included for VH signal. This part of the flood is captured by a temporary entity for the VV SITS. The VV SITS, however, includes a part of the flood in the east of the dynamic zone within its permanent entity, while this area is part of a temporary entity in the VH SITS (Figure 16). This dispersion of objects over different entities has to be taken into account when comparing variation values. Temporal profile and variation of permanent entities within the dynamic zone are depicted in Figure 17 for the ascending SITS.

Descending SITS

A similar dispersion of objects over different entities appears in the descending SITS (Figure 18). Part of the flood south-west of the Schulensmeer in not captured by the graph in the VV polarisation during timesteps 3–7. This part of the flood area is included in a temporary entity (green polygons in Figure 18). Temporal profile and evolution of variation of this temporary entity is shown in Figure 19. Similar to the ascending SITS, the VV polarisation includes a part of the flood in the east of the dynamic zone within its permanent entity, while this area is part of a temporary entity in the VH SITS (Figure 18). Again, this dispersion of objects over different entities implies that the global variation parameter, calculated for the temporal profile of the permanent entity, does not represent the variation of the whole flood zone, and that it is not possible to compare variation values for the dynamic zone over the different polarisations. Temporal profile and variation of permanent entities within the dynamic zone are depicted in Figure 20 for the descending SITS.

5. Discussion

This method proves to be a useful tool to gain insight in a flood event. Because the framework uses (freely available) Sentinel-1 images, it has operational potential. Graph-construction helps to identify entities present in the study site, the global variation maps delineate zones of high dynamics, while the temporal profiles describe the evolution of entities. This experiment confirms the findings of Guttler et al. [12] and Khiali et al. [13] in how the extracted information can be deeply explored at the evolution graph scale, as well as at the global study site scale.

However, the quality of the temporal profiles and variation values are intertwined with the quality of the segmentation results. Water body mapping is a complex topic on which much research is being done. Difficulties include the inefficient identification of mixed water pixels, confusion with background noise, and variation in threshold values according to the location and time of the image acquisitions [2,3,4,5,6,7,8,10]. In this research, delineating water bodies is done by an active contour model with parameters chosen by trial and error (Section 3.2). Optimal parameter values are dependent of the spatial distribution of flood zones, e.g., when there are numerous small flood zones, it is important to have pixel seeds within all these flooded zones [32]. This might be the problem in the static zone (Figure 11 and Figure 14), where the ACM fails to produce proper segmentation results at certain timesteps (timestep 2 in the ascending SITS, and timestep 3 in the descending SITS). This consecutively introduces variation in the evolution description which is not originating from changes on the ground. Improvement of the segmentation would improve the overall results of the presented method. This might be achieved by a more extensive trial and error phase, while choosing the parameters for the ACM, or by opting for other, often more labour-intensive, segmentation algorithms, such as supervised classifiers [34].

While the HH polarisation has the greatest potential for delineating floods consistently and accurately [7,35], Sentinel-1 collects images only in VH and VV polarisation when in IW mode (Interferometric Wide swath mode). For future research, it would be interesting to test the presented method, including the ACM, on the HH polarised signal which is currently only acquired by few SAR satellites (ALOS, Radarsat, TerraSAR-X) and not freely available. While VV polarisation provides a slight advantage for flood delineation compared to the VH polarisation, the VV polarisation is more susceptible to roughening of the water surface caused by rain or wind [15,18].

This is confirmed when the prevailing weather conditions (Figure 21) are compared with the segmentation results. A combination of precipitation and high wind speeds (at timestep 2 in the ascending SITS and at timestep 3 in the descending SITS), increases the roughness of the water surface which leads to a higher amount of backscatter. This is also visible on the global temporal profiles (Figure 7). In addition, different incidence angles due to different orbits during image capturing can result in deviant backscatter values (see Table 1).

Graph representation of the SITS results in three graph categories. The full graphs describe water entities which are present throughout the entire time series, incomplete graphs represent temporary entities, and one-node graphs represent unconnected polygons. If comparing variations for consecutive timesteps, one must keep in mind that the timesteps not always represent regular intervals (see Table 1). For instance, the shortest timestep in the ascending time series represents five days, while the longest timestep represents 17 days! In future research, it might be interesting to take the varying timestep length into account when calculating the variation between timesteps.

Polygons in the category unconnected (one-node graphs) can represent false positives (faulty detection of water) due to radar artefacts (such as double-bounce and vegetation interference) or faulty segmentation (failing ACM), yet it is also possible that these polygons form highly dynamic flood regions which are only present for a short period of time. This framework will not identify these high dynamic zones as such. However, the possibility that unconnected polygons are misclassified as water polygons increases, as they display high backscatter values (Figure 7 and Figure 8). Comparing these findings with ground truth or other classification/segmentation models could provide insight in this phenomenon.

When evaluating the calculated variation values, with reference to Figure 9, high variation values appear for the static zone in both ascending and descending VV signals, while the canal in the static zone is expected to display low variation. This, again, is due to the unsatisfactory segmentation results, particularly for the VV signals. The same trend appears in Table 2, which shows unexpected values for the VV signals. The descending VV signal the $GlobVar$ value for the dynamic zone is lower than the $GlobVar$ value for the static zone. This is due to the unstable segmentation in the static zone on the one hand, and the fact that not the whole flood area is captured within one entity on the other hand (cfr. compare timestep 4 of both descending VV and VH signals in the dynamic zone in Figure 18). Furthermore, $GlobVar$ for the whole study site is higher for the ascending SITS, while it comprises less timesteps. This can be partially explained by the number of polygons (see Table 2), i.e., a higher number of polygons results in higher variation values.

Overall, the graph-representation has great potential for a fast analysis of a flood event, delineating zones of high dynamics, and providing a relative quantification of local variations. Moreover, the method generates different outputs (temporal profiles, global variation maps, area evolution) that provide insights in the flood event. The presented method is, however, limited by its dependency of the segmentation algorithm. Furthermore, unconnected polygons are not taken into account for the calculation of the (global) variation, just as the timestep length is ignored in the current approach.

6. Conclusions

In this paper we have adapted an existing methodological framework that combines OBIA image processing and data mining techniques to extract spatio-temporal information. An active contour model is applied on SAR SITS generating separate sets of objects for each timestep. Subsequently, a graph-based approach is employed to detect and define spatially coherent entities and describe their spatio-temporal evolution through temporal profiles and global variation maps. The framework produces good results when water body delineation generates consistent objects. This crucial step, however, is affected by numerous intertwined factors, such as polarisation, prevailing weather conditions, orbit, ACM parameters, etc.

Future research plans consist of upscaling this research framework. Edge-effects (such as unconnected polygons, disconnection between flood areas, and noise effects) are expected to reduce when working on a larger scale. While the current study area is about 70 km${}^2$, the detection of spatio-temporal dynamics will be tested on an area of about 1000 km${}^2$, such as the flood event of 2019 in Beira, Mozambique.