LiDAR DEM Smoothing and the Preservation of Drainage Features
Abstract
:1. Introduction
2. Materials and Methods
2.1. Feature-Preserving DEM Smoothing (FPDEMS)
2.2. Study Site and Data
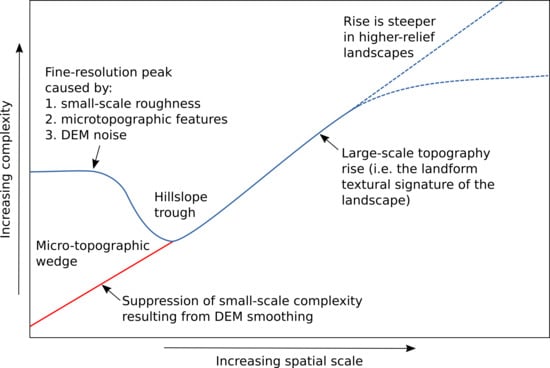
2.3. Circular Variance of Aspect and Surface Complexity Scale Signatures
3. Results
3.1. FPDEMS Parameter Selection
3.2. Comparison With Other DEM Smoothing Methods
3.3. Implications For Flow-Path Modelling
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baltsavias, E.P. A comparison between photogrammetry and laser scanning. Isprs J. Photogramm. Remote Sens. 1999, 54, 83–94. [Google Scholar] [CrossRef]
- Hodgson, M.E.; Bresnahan, P. Accuracy of airborne lidar-derived elevation. Photogramm. Eng. Remote Sens. 2004, 70, 331–339. [Google Scholar] [CrossRef]
- Yang, P.; Ames, D.P.; Fonseca, A.; Anderson, D.; Shrestha, R.; Glenn, N.F.; Cao, Y. What is the effect of LiDAR-derived DEM resolution on large-scale watershed model results? Environ. Model. Softw. 2014, 58, 48–57. [Google Scholar] [CrossRef]
- Brubaker, K.M.; Myers, W.L.; Drohan, P.J.; Miller, D.A.; Boyer, E.W. The use of LiDAR terrain data in characterizing surface roughness and microtopography. Appl. Environ. Soil Sci. 2013, 2013, 1–13. [Google Scholar] [CrossRef]
- MacMillan, R.A.; Martin, T.C.; Earle, T.J.; McNabb, D.H. Automated analysis and classification of landforms using high-resolution digital elevation data: applications and issues. Can. J. Remote Sens. 2003, 29, 592–606. [Google Scholar] [CrossRef]
- Lindsay, J.B.; Creed, I.F. Sensitivity of digital landscapes to artifact depressions in remotely-sensed DEMs. Photogramm. Eng. Remote Sens. 2005, 71, 1029–1036. [Google Scholar] [CrossRef]
- Grohmann, C.H.; Smith, M.J.; Riccomini, C. Multiscale analysis of topographic surface roughness in the Midland Valley, Scotland. IEEE Trans. Geosci. Remote Sens. 2010, 49, 1200–1213. [Google Scholar] [CrossRef]
- Lindsay, J.B.; Newman, D.R. Hyper-scale analysis of surface roughness. Peer J Prepr. 2018, 6, e27110v1. [Google Scholar]
- Reuter, H.I.; Hengl, T.; Gessler, P.; Soille, P. Chapter 4 Preparation of DEMs for geomorphometric analysis. Dev. Soil Sci. 2009, 33, 87–120. [Google Scholar]
- Habtezion, N.; Tahmasebi Nasab, M.; Chu, X. How does DEM resolution affect microtopographic characteristics, hydrologic connectivity, and modelling of hydrologic processes? Hydrol. Process. 2016, 30, 4870–4892. [Google Scholar] [CrossRef]
- Deng, Y.; Wilson, J.P.; Bauer, B.O. DEM resolution dependencies of terrain attributes across a landscape. Int. J. Geogr. Inf. Sci. 2007, 21, 187–213. [Google Scholar] [CrossRef]
- Tian, B.; Wang, L.; Koike, K. Spatial statistics of surface roughness change derived from multi-scale digital elevation models. Procedia Environ. Sci. 2011, 7, 252–257. [Google Scholar] [CrossRef] [Green Version]
- Stevenson, J.A.; Sun, X.; Mitchell, N.C. Despeckling SRTM and other topographic data with a denoising algorithm. Geomorphology 2010, 114, 238–252. [Google Scholar] [CrossRef]
- Zakšek, K.; Podobnikar, T. An effective DEM generalization with basic GIS operations. In Proceedings of the 8th ICA WORKSHOP on Generalisation and Multiple Representation, A Coruńa, Spain, 7–8 July 2005; the International Cartographic Association (ICA): Bern, Switzerland, 2005; p. 10. [Google Scholar]
- Lindsay, J.B. Whitebox GAT: A case study in geomorphometric analysis. Comput. Geosci. 2016, 95, 75–84. [Google Scholar] [CrossRef]
- Grohmann, C.H. Effects of spatial resolution on slope and aspect derivation for regional-scale analysis. Comput. Geosci. 2015, 77, 111–117. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Wilson, J.P.; Zhu, Q.; Zhou, Q. Comparison of drainage-constrained methods for DEM generalization. Comput. Geosci. 2012, 48, 41–49. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, Q. A scale-adaptive DEM for multi-scale terrain analysis. Int. J. Geogr. Inf. Sci. 2013, 27, 1329–1348. [Google Scholar] [CrossRef]
- Ai, T.; Li, J. A DEM generalization by minor valley branch detection and grid filling. Isprs J. Photogramm. Remote Sens. 2010, 65, 198–207. [Google Scholar] [CrossRef]
- Walker, J.P.; Willgoose, G.R. On the effect of digital elevation model accuracy on hydrology and geomorphology. Water Resour. Res. 1999, 35, 2259–2268. [Google Scholar] [CrossRef] [Green Version]
- Gallant, J. Adaptive smoothing for noisy DEMs. In Proceedings of the Geomorphometry 2011, Redlands, CA, USA, 7–8 September 2011. [Google Scholar]
- Barash, D. A fundamental relationship between bilateral filtering, adaptive smoothing, and the nonlinear diffusion equation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 26, 844–847. [Google Scholar] [CrossRef]
- Usul, N.; Pasaogullari, O. Effect of map scale and grid size for hydrological modelling. Iahs Publ. 2004, 289, 91–100. [Google Scholar]
- Petrasova, A.; Mitasova, H.; Petras, V.; Jeziorska, J. Fusion of high-resolution DEMs for water flow modeling. Open Geospat. Datasoftware Stand. 2017, 2, 6. [Google Scholar] [CrossRef]
- Harwood, D.; Subbarao, M.; Hakalahti, H.; Davis, L.S. A new class of edge-preserving smoothing filters. Pattern Recognit. Lett. 1987, 6, 155–162. [Google Scholar] [CrossRef]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. Proc. Iccv 1998, 98, 2. [Google Scholar]
- Paris, S.; Kornprobst, P.; Tumblin, J.; Durand, F. Bilateral filtering: Theory and applications. Found. Trends® Comput. Graph. Vis. 2009, 4, 1–73. [Google Scholar] [CrossRef]
- Fleishman, S.; Drori, I.; Cohen-Or, D. Bilateral mesh denoising. ACM 2003, 22, 950–953. [Google Scholar]
- Jones, T.R.; Durand, F.; Desbrun, M. Non-iterative, feature-preserving mesh smoothing. ACM 2003, 22, 943–949. [Google Scholar] [Green Version]
- Lee, K.-W.; Wang, W.-P. Feature-preserving mesh denoising via bilateral normal filtering. In Proceedings of the Ninth International Conference on Computer Aided Design and Computer Graphics (CAD-CG’05), Hong Kong, China, 7–10 December 2005; IEEE: Washington, DC, USA, 2005. [Google Scholar]
- Sun, X.; Rosin, P.L.; Martin, R.; Langbein, F. Fast and effective feature-preserving mesh denoising. IEEE Trans. Vis. Comput. Graph. 2007, 13, 925–938. [Google Scholar] [CrossRef]
- Zheng, Y.; Fu, H.; Au, O.K.-C.; Tai, C.-L. Bilateral normal filtering for mesh denoising. IEEE Trans. Vis. Comput. Graph. 2010, 17, 1521–1530. [Google Scholar] [CrossRef]
- Horn, B.K. Hill shading and the reflectance map. Proc. IEEE 1981, 69, 14–47. [Google Scholar] [CrossRef] [Green Version]
- Lindsay, J.B. WhiteboxTools User Manual. Available online: https://jblindsay.github.io/wbt_book/preface.html (accessed on 16 August 2019).
- Chapman, L.J.; Putnam, D.F. Physiography of Southern Ontario; University of Toronto Press: Toronto, ON, Canada, 1973; p. 284. [Google Scholar]
- MNRF User Guide: Lidar Point Cloud (2016-18) LIO Dataset v. 1.3. Available online: https://www.sse.gov.on.ca/sites/MNR-PublicDocs/EN/CMID/Lidar%20Point%20Cloud%20-%20User%20Guide.pdf (accessed on 16 August 2019).
- Tarboton, D.G. A new method for the determination of flow directions and upslope areas in grid digital elevation models. Water Resour. Res. 1997, 33, 309–319. [Google Scholar] [CrossRef] [Green Version]
- James, L.A.; Watson, D.G.; Hansen, W.F. Using LiDAR data to map gullies and headwater streams under forest canopy: South Carolina, USA. Catena 2007, 71, 132–144. [Google Scholar] [CrossRef]
- Govers, G.; Takken, I.; Helming, K. Soil roughness and overland flow. Agronomie 2000, 20, 131–146. [Google Scholar] [CrossRef]
- Govers, G.; Giménez, R.; Van Oost, K. Rill erosion: exploring the relationship between experiments, modelling and field observations. Earth-Sci. Rev. 2007, 84, 87–102. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Dietrich, W.E. Source areas, drainage density, and channel initiation. Water Resour. Res. 1989, 25, 1907–1918. [Google Scholar] [CrossRef] [Green Version]











| Parameter | Value | Time (s) |
|---|---|---|
| Kernel size | 11 × 11 | 155.4 |
| (grid cells) | 17 × 17 | 228.4 |
| 25 × 25 | 394.6 | |
| 31 × 31 | 566.7 | |
| 51 × 51 | 1330.7 | |
| Threshold | 5.0° | 246.8 |
| (degrees) | 10.0° | 234.6 |
| 15.0° | 230.3 | |
| 25.0° | 237.7 | |
| 50.0° | 232.1 | |
| Iterations | 1 | 176.7 |
| 3 | 232.0 | |
| 5 | 277.8 | |
| 7 | 338.2 | |
| 10 | 403.8 |
| Method | Value (Grid Cells) | Time (s) |
|---|---|---|
| Mean | 3 × 3 | 16.1 |
| 5 × 5 | 15.0 | |
| 7 × 7 | 15.0 | |
| 9 × 9 | 15.0 | |
| 11 × 11 | 14.9 | |
| 15 × 15 | 16.0 | |
| 21 × 21 | 15.1 | |
| Median | 3 × 3 | 15.5 |
| 5 × 5 | 15.9 | |
| 7 × 7 | 16.7 | |
| 9 × 9 | 16.7 | |
| 11 × 11 | 17.1 | |
| 15 × 15 | 18.3 | |
| 21 × 21 | 20.3 | |
| Gaussian | Sigma = 0.3 | 18.7 |
| Sigma = 0.7 | 23.3 | |
| Sigma = 1.0 | 31.9 | |
| Sigma = 1.3 | 42.3 | |
| Sigma = 1.7 | 56.9 | |
| Sigma = 2.3 | 91.0 | |
| Sigma = 3.3 | 150.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lindsay, J.B.; Francioni, A.; Cockburn, J.M.H. LiDAR DEM Smoothing and the Preservation of Drainage Features. Remote Sens. 2019, 11, 1926. https://doi.org/10.3390/rs11161926
Lindsay JB, Francioni A, Cockburn JMH. LiDAR DEM Smoothing and the Preservation of Drainage Features. Remote Sensing. 2019; 11(16):1926. https://doi.org/10.3390/rs11161926
Chicago/Turabian StyleLindsay, John B., Anthony Francioni, and Jaclyn M. H. Cockburn. 2019. "LiDAR DEM Smoothing and the Preservation of Drainage Features" Remote Sensing 11, no. 16: 1926. https://doi.org/10.3390/rs11161926
APA StyleLindsay, J. B., Francioni, A., & Cockburn, J. M. H. (2019). LiDAR DEM Smoothing and the Preservation of Drainage Features. Remote Sensing, 11(16), 1926. https://doi.org/10.3390/rs11161926