Nowcasting of Surface Solar Irradiance Using FengYun-4 Satellite Observations over China
Abstract
:1. Introduction
2. Data Pre-Processing
2.1. FY-4A Satellite Data
2.2. Ground Data
2.3. Clear Sky Irradiance Model (ESRA)
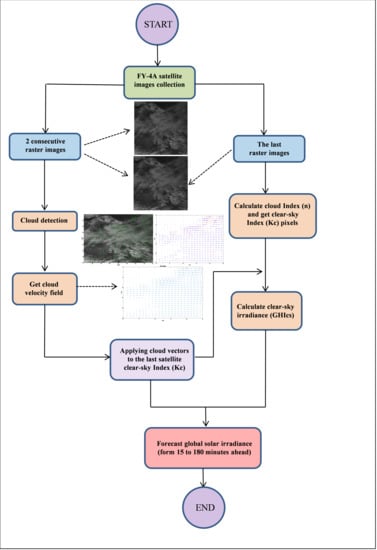
3. Methodology
3.1. Statistical Extrapolation Method
3.2. Cloud Tracking-Particle Image Velocimetry
4. Statistical Index for Accuracy Evaluation
5. Results and Discussion
5.1. Results under Clear Sky Conditions
5.2. Results under Partly Cloudy Conditions
5.3. Results under Overcast Conditions
5.4. Results under Snowy-Sky Conditions
5.5. Results under All Sky Conditions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, M.; Hu, Z.; Tan, X.; Shan, B. Scenario analysis on mid-long term energy and electricity demand and carbon emission in China. Electr. Power 2012, 45, 101–107. (In Chinese) [Google Scholar]
- Lin, B.; Yang, F.; Liu, X. A study of the rebound effect on China’s current energy conservation and emissions reduction: Measures and policy choices. Energy 2013, 58, 330–339. [Google Scholar] [CrossRef]
- Sanchez-Lorenzo, A.; Enriquez-Alonso, A.; Wild, M.; Trentmann, J.; Vicente-Serrano, S.M.; Sanchez-Romero, A.; Posselt, R.; Hakuba, M.Z. Trends in downward surface solar radiation from satellites and ground observations over Europe during 1983–2010. Remote Sens. Environ. 2017, 189, 108–117. [Google Scholar] [CrossRef]
- Khatib, T.; Mohamed, A.; Sopian, K. A review of solar energy modeling techniques. Renew. Sustain. Energy Rev. 2012, 16, 2864–2869. [Google Scholar] [CrossRef]
- Benghanem, M.; Mellit, A. Radial Basis Function Network-based prediction of global solar radiation data: Application for sizing of a stand-alone photovoltaic system at Al-Madinah, Saudi Arabia. Energy 2010, 35, 3751–3762. [Google Scholar] [CrossRef]
- Yang, D.; Kleissl, J.; Gueymard, C.A.; Pedro, H.T.; Coimbra, C.F. History and trends in solar irradiance and pv power forecasting: A preliminary assessment and review using text mining. Sol. Energy 2018, 168, 60–101. [Google Scholar] [CrossRef]
- Wild, M.; Folini, D.; Henschel, F.; Fischer, N.; Müller, B. Projections of long term changes in solar radiation based on CMIP5 climate models and their influence on energy yields of photovoltaic systems. Sol. Energy 2015, 116, 12–24. [Google Scholar] [CrossRef]
- Bernecker, D.; Riess, C.; Angelopoulou, E.; Hornegger, J. Continuous short-term irradiance forecasts using sky images. Sol. Energy 2014, 110, 303–315. [Google Scholar] [CrossRef]
- Rosiek, S.; Alonso-Montesinos, J.; Batlles, F.J. Online 3-h forecasting of the power output from a BIPV system using satellite observations and ANN. Int. J. Electr. Power 2018, 99, 261–272. [Google Scholar] [CrossRef]
- Gallucci, D.; Romano, F.; Cersosimo, A.; Cimini, D.; Viggiano, M. Nowcasting surface solar irradiance with AMESIS via motion vector fields of MSG-SEVIRI data. Remote Sens. 2018, 10, 845. [Google Scholar] [CrossRef]
- Caldas, M.; Alonso-Suárez, R. Very short-term solar irradiance forecast using all-sky imaging and real-time irradiance measurements. Renew. Energy 2019, 143, 1643–1658. [Google Scholar] [CrossRef]
- Kamadinata, O.J.; Ken, T.L.; Suwa, T. Sky image-based solar irradiance prediction methodologies using artificial neural networks. Renew. Energy 2019, 134, 837–845. [Google Scholar] [CrossRef]
- Benali, L.; Notton, G.; Fouilloy, A.; Voyant, C.; Dizene, R. Solar radiation forecasting using artificial neural network and random forest methods: Application to normal beam, horizontal diffuse and global components. Renew. Energy 2019, 132, 871–884. [Google Scholar] [CrossRef]
- Miller, S.D.; Rogers, M.A.; Haynes, J.M.; Sengupta, M.; Heidinger, A.K. Short-term solar irradiance forecasting via satellite/model coupling. Sol. Energy 2017, 168, 102–117. [Google Scholar] [CrossRef]
- Arbizu-Barrena, C.; Ruiz-Arias, J.A.; Rodríguez-Benítez, F.J.; Pozo-Vázquez, D.; Tovar-Pescador, J. Short-term solar radiation forecasting by advecting and diffusing MSG cloud index. Sol. Energy 2017, 155, 1092–1103. [Google Scholar] [CrossRef]
- Wang, P.; van Westrhenen, R.; Meirink, J.F.; van der Veen, S.; Knap, W. Surface solar radiation forecasts by advecting cloud physical properties derived from Meteosat Second Generation observations. Sol. Energy 2019, 177, 47–58. [Google Scholar] [CrossRef]
- Bai, T.; Li, D.; Sun, K.; Chen, Y.; Li, W. Cloud detection for high-resolution satellite imagery using machine learning and multi-feature fusion. Remote Sens. 2016, 8, 715. [Google Scholar] [CrossRef]
- Rigollier, C.; Lefèvre, M.; Wald, L. The method Heliosat-2 for deriving shortwave solar radiation from satellite images. Sol. Energy 2004, 77, 159–169. [Google Scholar] [CrossRef] [Green Version]
- Mouhamet, D.; Tommy, A.; Primerose, A.; Laurent, L. Improving the Heliosat-2 method for surface solar irradiation estimation under cloudy sky areas. Sol. Energy 2018, 169, 565–576. [Google Scholar] [CrossRef]
- Hammer, A.; Kühnert, J.; Weinreich, K.; Lorenz, E. Short-term forecasting of surface solar irradiance based on Meteosat-SEVIRI data using a nighttime cloud index. Remote Sens. 2015, 7, 9070–9090. [Google Scholar] [CrossRef]
- Gallucci, D.; Romano, F.; Cimini, D.; Di Paola, F.; Gentile, S.; Larosa, S.; Nilo, S.; Ricciardelli, E.; Ripepi, E.; Viggiano, M.; et al. Improvement of Hourly Surface Solar Irradiance Estimation Using MSG Rapid Scanning Service. Remote Sens. 2019, 11, 66. [Google Scholar] [CrossRef]
- Zhai, H.; Zhang, H.; Zhang, L.; Li, P. Cloud/shadow detection based on spectral indices for multi/hyperspectral optical remote sensing imagery. ISPRS J. Photogramm. 2018, 144, 235–253. [Google Scholar] [CrossRef]
- Fan, L.; Wei, Z.; Dong, W.; Wei, G. Preliminary Study on Surface Radiation Properties in Arid Region of Northwest China. Plateau Meteorol. 2002, 21, 309–314. (In Chinese) [Google Scholar] [CrossRef]
- Zheng, Z.; Wei, Z.; Li, Z.; Wang, C. Characteristics of solar spectral radiation and albedo during early autumn in Dunhuang gobi. Acta Energiae Sol. Sin. 2012, 33, 1937–1943. (In Chinese) [Google Scholar] [CrossRef]
- Rigollier, C.; Bauer, O.; Wald, L. On the clear sky model of the ESRA—European Solar Radiation Atlas—With respect to the heliosat method. Sol. Energy 2000, 68, 33–48. [Google Scholar] [CrossRef]
- Ineichen, P. Conversion function between the Linke turbidity and the atmospheric water vapor and aerosol content. Sol. Energy 2008, 82, 1095–1097. [Google Scholar] [CrossRef] [Green Version]
- Voyant, C.; Soubdhan, T.; Lauret, P.; David, M.; Muselli, M. Statistical parameters as a means to a priori assess the accuracy of solar forecasting models. Energy 2015, 90, 671–679. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Ruan, X.; Yang, H. Development and application of MPIV software for PIV on the vasis of MATLAB. Mech. Electr. Eng. Mag. 2005, 22, 1–4. (In Chinese) [Google Scholar] [CrossRef]
- Nonnenmacher, L.; Coimbra, C.F.M. Streamline-based method for intra-day solar forecasting through remote sensing. Sol. Energy 2014, 108, 447–459. [Google Scholar] [CrossRef]
- Mori, N.; Chang, K.A. Introduction to MPIV, 2003. Available online: http://www.oceanwave.jp/softwares/mpiv (accessed on 20 March 2019).
- Marquez, R.; Coimbra, C.F.M. Proposed metric for evaluation of solar forecasting models. J. Sol. Energy Eng. 2012, 135, 1–9. [Google Scholar] [CrossRef]
- Moradi, I.; Mueller, R.; Alijani, B.; Kamali, G.A. Evaluation of the Heliosat-II method using daily irradiation data for four stations in Iran. Sol. Energy 2009, 83, 150–156. [Google Scholar] [CrossRef]
- Alonso-Montesinos, J.; Batlles, F.J.; Bosch, J.L. Beam, Diffuse and global solar irradiance estimation with satellite imagery. Energy Convers. Manag. 2015, 105, 1205–1212. [Google Scholar] [CrossRef]
- Romano, F.; Cimini, D.; Cersosimo, A.; Di Paola, F.; Gallucci, D.; Gentile, S.; Geraldi, E.; Larosa, S.; Nilo, S.T.; Ricciardelli, E.; et al. Improvement in Surface Solar Irradiance Estimation Using HRV/MSG Data. Remote Sens. 2018, 10, 1288. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M.; Adamowski, J.F.; Mi, J. Universally deployable extreme learning machines integrated with remotely sensed MODIS satellite predictors over Australia to forecast global solar radiation: A new approach. Renew. Sustain. Energy Rev. 2019, 104, 235–261. [Google Scholar] [CrossRef]
- Wang, F.; Mi, Z.; Zhen, Z.; Yang, G.; Zhou, H. A classified forecasting approach of power generation for photovoltaic plants based on weather condition pattern recognition. Proc. CSEE 2013, 33, 75–82. (In Chinese) [Google Scholar] [CrossRef]
- Sun, X.; Bright, J.M.; Gueymard, C.A.; Acord, B.; Wang, P.; Engerer, N.A. Worldwide performance assessment of 75 global clear sky irradiance models using Principal Component Analysis. Renew. Sustain. Energy Rev. 2019, 111, 550–570. [Google Scholar] [CrossRef]
- Zhao, S.; Gao, X. Study of Aerosol Optical Depth and Angstrom Exponent in the Northwest of China Based on MODIS Product. J. Atmos. Environ. Opt. 2017, 12, 321–331. (In Chinese) [Google Scholar] [CrossRef]
- Shi, F.; Xin, J.; Yang, L.; Cong, Z.; Liu, R.; Ma, Y.; Wang, Y.; Lu, X.; Zhao, L. The first validation of the precipitable water vapor of multisensor satellites over the typical regions in China. Remote Sens. Environ. 2018, 206, 107–122. [Google Scholar] [CrossRef]
- Gui, K.; Che, H.; Chen, Q.; Zeng, Z.; Zheng, Y.; Long, Q.; Sun, T.; Liu, X.; Wang, Y.; Liao, T.; et al. Water vapor variation and the effect of aerosols in China. Atmos. Environ. 2017, 322–335. [Google Scholar] [CrossRef]
- Lara-Fanego, V.; Ruiz-Arias, J.A.; Pozo-Vázquez, D.; Santos-Alamillos, F.J.; Tovar Pescador, J. Evaluation of the WRF model solar irradiance forecasts in Andalusia (Southern Spain). Sol. Energy 2012, 86, 2200–2217. [Google Scholar] [CrossRef]
- Cornejo-Bueno, L.; Casanova-Mateo, C.; Sanz-Justo, J.; Salcedo-Sanz, S. Machine learning regressors for solar radiation estimation from satellite data. Sol. Energy 2019, 183, 768–775. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, W.; Yao, J.; Wang, W. Variation of cloud fraction and its relationship with solar radiation over semi-arid region. J. Arid Meteorol. 2015, 33, 684–693. (In Chinese) [Google Scholar] [CrossRef]
- Xia, S.; Mestas-Nuñez, A.M.; Xie, H.; Tang, J.; Vega, R. Characterizing Variability of Solar Irradiance in San Antonio, Texas Using Satellite Observations of Cloudiness. Remote Sens. 2018, 10, 2016. [Google Scholar] [CrossRef]
- Blaga, R.; Sabadus, A.; Stefu, N.; Dughir, C.; Paulescu, M.; Badescu, V. A current perspective on the accuracy of incoming solar energy forecasting. Prog. Energy Combust. 2019, 70, 119–144. [Google Scholar] [CrossRef]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]









| RMSE | nRMSE (%) | MAE | nMAE (%) | MBE | nMBE (%) | |
|---|---|---|---|---|---|---|
| GHI | 14.48 | 3.62 | 10.02 | 2.51 | 4.27 | 1.07 |
| Metric | Model | t + 15 min | t + 30 min | t + 45 min | t + 60 min | t + 120 min | t + 180 min |
|---|---|---|---|---|---|---|---|
| RMSE | SP | 73.27 | 90.4 | 97.8 | 102.61 | 126.53 | 135.23 |
| FY-4A | 79.02 | 82.62 | 79.89 | 82.23 | 85.09 | 82.18 | |
| nRMSE (%) | SP | 20.3 | 25.03 | 27.08 | 28.14 | 35.04 | 38.45 |
| FY-4A | 21.08 | 22.17 | 21.76 | 23.01 | 24.89 | 22.76 | |
| MAE | SP | 51.43 | 65.9 | 72.31 | 76.51 | 95.95 | 97.28 |
| FY-4A | 66.47 | 68.29 | 65.36 | 65.62 | 70.01 | 63.1 | |
| nMAE (%) | SP | 14.24 | 18.25 | 20.03 | 21.19 | 26.57 | 27.12 |
| FY-4A | 17.3 | 18.33 | 17.8 | 17.73 | 18.5 | 17.48 | |
| MBE | SP | 2.03 | 4.45 | 6.84 | 9.05 | 16.38 | 25.03 |
| FY-4A | 5.12 | 7.61 | 12.15 | 12.11 | 23.54 | 32.24 | |
| nMBE (%) | SP | 0.56 | 1.23 | 1.89 | 2.51 | 4.54 | 6.89 |
| FY-4A | 1.36 | 2.04 | 3.31 | 3.27 | 6.32 | 8.93 |
| Metric | Model | t + 15 min | t + 30 min | t + 45 min | t + 60 min | t + 120 min | t + 180 min |
|---|---|---|---|---|---|---|---|
| RMSE | SP | 90.05 | 103.51 | 124.07 | 117.83 | 123.42 | 146.15 |
| FY-4A | 97.63 | 96.74 | 94.54 | 93.81 | 105.03 | 116.75 | |
| nRMSE (%) | SP | 29.90 | 34.36 | 41.19 | 39.12 | 41.24 | 48.54 |
| FY-4A | 32.41 | 32.11 | 31.39 | 31.14 | 34.87 | 38.78 | |
| MAE | SP | 67.08 | 74.40 | 92.75 | 86.44 | 90.12 | 104.11 |
| FY-4A | 78.11 | 76.74 | 74.10 | 74.29 | 79.54 | 87.46 | |
| nMAE (%) | SP | 22.27 | 24.70 | 30.80 | 28.70 | 29.91 | 34.56 |
| FY-4A | 25.93 | 25.48 | 24.61 | 24.67 | 26.41 | 29.03 | |
| MBE | SP | 0.20 | 1.34 | 2.71 | 4.61 | 14.63 | 30.66 |
| FY-4A | 40.01 | 39.19 | 38.45 | 37.00 | 47.09 | 57.86 | |
| nMBE (%) | SP | 0.07 | 0.45 | 0.90 | 1.52 | 4.86 | 10.18 |
| FY-4A | 13.30 | 13.01 | 12.76 | 12.28 | 15.63 | 19.21 |
| Metric | Model | t + 15 min | t + 30 min | t + 45 min | t + 60 min | t + 120 min | t + 180 min |
|---|---|---|---|---|---|---|---|
| RMSE | SP | 75.69 | 90.03 | 99.48 | 109.23 | 140.51 | 156.48 |
| FY-4A | 108.02 | 109.32 | 110.06 | 109.59 | 112.04 | 120.82 | |
| nRMSE (%) | SP | 30.12 | 37.12 | 40.01 | 42.92 | 56.89 | 65.33 |
| FY-4A | 43.79 | 44.37 | 45.05 | 44.64 | 45.61 | 49.21 | |
| MAE | SP | 47.01 | 57.51 | 63.63 | 89.12 | 100.01 | 111.02 |
| FY-4A | 91.09 | 91.99 | 94.85 | 92.31 | 93.23 | 103.93 | |
| nMAE (%) | SP | 19.14 | 23.02 | 26.82 | 35.76 | 40.58 | 45.02 |
| FY-4A | 37.19 | 37.39 | 38.84 | 37.60 | 38.02 | 42.33 | |
| MBE | SP | 9.5 | 3.01 | 4.51 | 9.09 | 14.24 | 23.27 |
| FY-4A | 55.13 | 54.12 | 56.61 | 54.42 | 66.15 | 83.34 | |
| nMBE (%) | SP | 1.91 | 1.23 | 1.83 | 3.84 | 5.80 | 10.29 |
| FY-4A | 21.87 | 22.05 | 23.06 | 22.17 | 27.01 | 33.95 |
| Metric | Model | t + 15 min | t + 30 min | t + 45 min | t + 60 min | t + 120 min | t + 180 min |
|---|---|---|---|---|---|---|---|
| RMSE | SP | 54.58 | 63.95 | 72.58 | 79.43 | 92.99 | 113.54 |
| FY-4A | 61.28 | 61.78 | 62.05 | 60.89 | 67.18 | 68.61 | |
| nRMSE (%) | SP | 17.01 | 20.02 | 22.73 | 24.88 | 29.12 | 35.56 |
| FY-4A | 19.01 | 19.11 | 19.20 | 18.93 | 21.07 | 21.59 | |
| MAE | SP | 33.19 | 40.41 | 46.00 | 51.05 | 61.14 | 73.61 |
| FY-4A | 45.26 | 45.76 | 45.72 | 44.87 | 49.93 | 50.21 | |
| nMAE (%) | SP | 11.08 | 12.65 | 14.40 | 15.99 | 19.15 | 23.06 |
| FY-4A | 14.12 | 14.16 | 14.14 | 13.96 | 15.84 | 15.99 | |
| MBE | SP | −0.83 | −1.80 | −2.64 | −3.36 | −3.85 | −0.13 |
| FY-4A | 11.39 | 11.50 | 11.58 | 9.84 | 14.79 | 14.83 | |
| nMBE (%) | SP | −0.26 | −0.56 | −0.83 | −1.05 | −1.21 | −0.04 |
| FY-4A | 3.39 | 3.56 | 3.58 | 3.18 | 4.74 | 4.87 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Gao, X.; Li, Z.; Jia, D.; Jiang, J. Nowcasting of Surface Solar Irradiance Using FengYun-4 Satellite Observations over China. Remote Sens. 2019, 11, 1984. https://doi.org/10.3390/rs11171984
Yang L, Gao X, Li Z, Jia D, Jiang J. Nowcasting of Surface Solar Irradiance Using FengYun-4 Satellite Observations over China. Remote Sensing. 2019; 11(17):1984. https://doi.org/10.3390/rs11171984
Chicago/Turabian StyleYang, Liwei, Xiaoqing Gao, Zhenchao Li, Dongyu Jia, and Junxia Jiang. 2019. "Nowcasting of Surface Solar Irradiance Using FengYun-4 Satellite Observations over China" Remote Sensing 11, no. 17: 1984. https://doi.org/10.3390/rs11171984
APA StyleYang, L., Gao, X., Li, Z., Jia, D., & Jiang, J. (2019). Nowcasting of Surface Solar Irradiance Using FengYun-4 Satellite Observations over China. Remote Sensing, 11(17), 1984. https://doi.org/10.3390/rs11171984