Next Article in Journal
Clustering Coastal Land Use Sequence Patterns along the Sea–Land Direction: A Case Study in the Coastal Zone of Bohai Bay and the Yellow River Delta, China
Previous Article in Journal
Phenotyping of Corn Plants Using Unmanned Aerial Vehicle (UAV) Images
Previous Article in Special Issue
Reflectance Properties of Hemiboreal Mixed Forest Canopies with Focus on Red Edge and Near Infrared Spectral Regions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 11
Issue 17
10.3390/rs11172022
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Estimating Stand Age from Airborne Laser Scanning Data to Improve Models of Black Spruce Wood Density in the Boreal Forest of Ontario

by
Rebecca R.M. Wylie
1,
Murray E Woods
2 and
Jeffery P. Dech
1,*
1
Department of Biology and Chemistry, Nipissing University, North Bay, ON P1B 8L7, Canada
2
Ontario Ministry of Natural Resources and Forestry, Forest Resource Inventory Unit, North Bay, ON P1A 4L7, Canada
*
Author to whom correspondence should be addressed.
Remote Sens. 2019, 11(17), 2022; https://doi.org/10.3390/rs11172022
Submission received: 29 May 2019 / Revised: 5 August 2019 / Accepted: 23 August 2019 / Published: 28 August 2019
(This article belongs to the Special Issue Remote Sensing of Boreal Forests)
Browse Figures
Versions Notes

Abstract

:
Spatial models that provide estimates of wood quality enable value chain optimization approaches that consider the market potential of trees prior to harvest. Ecological land classification units (e.g., ecosite) and structural metrics derived from Airborne Laser Scanning (ALS) data have been shown to be useful predictors of wood quality attributes in black spruce stands of the boreal forest of Ontario, Canada. However, age drives much of the variation in wood quality among trees, and has not been included as a predictor in previous models because it is poorly represented in inventory systems. The objectives of this study were (i) to develop a predictive model of mean stem age of black spruce-dominated stands, and (ii) refine models of black spruce wood density by including age as a predictor variable. A non-parametric model of stand age that used a k nearest neighbor (kNN) classification based on a random forests (rf) distance metric performed well, producing a root mean square difference (RMSD) of 15 years and explaining 62% of the variance. The subsequent random forests model of black spruce wood density generated from age and ecosite predictors was useful, with a root mean square error (RMSE) of 59.1 kg·m−3. These models bring large-scale wood quality prediction closer to becoming operational by including age and site effects that can be derived from inventory data.

Graphical Abstract

1. Introduction

Airborne Laser Scanning (ALS) technology has become widely accepted as an important tool for enhancing forest resource inventory (FRI) systems by increasing the accuracy of vertical structural measurements [1]. Point clouds derived from ALS data have also been shown to support a variety of ecological modeling initiatives that use implicit relationships to forest structures to make predictions of variables that are traditionally measured or estimated in the FRI such as stand age [2], as well as novel variables that could be used to optimize the value chain such as tree-level estimates of wood quality attributes [3,4]. Adding general indicators of wood quality to FRI polygons would supply basic information about where certain attributes are concentrated on the landscape. This information could support harvesting decisions to reflect market trends, and may also be useful in facilitating broader management goals such as climate change planning [5].
Wood quality attributes are strongly linked to environmental driving factors [6]. Variation in environmental conditions among stands, and the resulting impact of these factors on wood quality, is often detectible through analysis of ALS data. This suggests that some wood properties could be indirectly predicted from remotely sensed ALS data, which creates the opportunity to add wood quality variables to FRI systems through spatial modeling [7]. From a modeling perspective, it is therefore important to understand the processes and mechanisms that drive spatial variation in the characteristics of woody tissues, and ultimately identify conditions that produce specific wood qualities (e.g., high density). There are tree and stand-level variables known to be useful indicators of wood quality, such as crown/canopy shape, stocking density, age, and site conditions, which can be derived from ALS point cloud data [2,4,7]. Wood density is an important general indicator of wood quality, related to marketable values such as stiffness, strength and hardness, which are important characteristics of products that are produced from wood [8]. Considering these possibilities has led to the development of models using site and ALS data to predict mean stand level wood density. Pokharel et al. [9] were able to use ecological land classification and mensuration variables described in a FRI to explain 44.1% of the variation in black spruce wood density in the first 50 years of growth, producing a model with a root mean square error (RMSE) of 40.4 kg·m−3. Pokharel et al. [4] predicted wood density using ALS structural metrics to explain 39% of the variation with a RMSE of 38.8 kg·m−3. In the boreal forest of Newfoundland, wood quality attributes were modeled using ALS structural, environmental and climate variables to predict wood density of black spruce with an RMSE of 20.9 kg·m−3 [3].
All of these predictive wood quality models in boreal forest were restricted in application, given that age could not be included as a predictor variable due to the poor representation of age in the respective FRI systems. The lack of age data required that the Ontario models be fit for only the first 50 years of growth, which limited their generalizability, since there is a far greater range in age than 50 years in any given boreal forest unit in Ontario. As the tree ages, the cambium matures and produces higher density cells in a radial transition from corewood (low density tissue near the pith) to outerwood (higher density tissue near the bark), which provides mechanical support in response to greater loads produced by the upward growth of the tree [10]. The shape of this radial profile of wood properties from corewood to outerwood changes depending on environmental factors [9]. For example, on sites that experience frequent drought, where protection from embolism of cells is an important selective pressure, the transition from corewood to outerwood occurs earlier [11]. Therefore, at any given age, the stem will contain a greater proportion of higher density outerwood than a comparable tree on a benign site that lacks drought. The interaction of these two factors, the developmental transition from corewood to outerwood, and the influence of site conditions, determine the relative proportion of high density wood in a given stem, and these factors are confounded when age is not included as a predictor variable.
Stand age in FRI systems is typically estimated based on a standard curve of stand height and tree age derived from a small number of field samples and linked to a photo interpretation for the majority of stands. This type of estimate works best in single species stands that are the first cohort of trees to be established after a stand-replacing disturbance [12]. However, in stands where there is a mix of cohorts, species, or in nutrient poor or flooded sites, the relationship between age and height becomes more ambiguous, especially when there are shade tolerant species involved [13]. In these cases there are many influences impacting the rate of growth, and the species-specific height curve is not necessarily a reliable predictor of age [12].
In single cohort stands and in places where there is a long, well documented history of forestry activities or the time since fire is adequately reported, forest stand age can be assigned [14]. However, in the boreal forest of Ontario, the disturbance history has not been well-documented. A promising approach to estimating age in these forest stands is to examine ALS data, which can provide accurate measurements of vertical canopy complexity, crown height, and surface roughness (rumple), all of which are indicators of successional stage [15,16]. A number of studies have attempted to use ALS metrics to assign age, time since stand replacing disturbance, or successional stage with varying degrees of success [2,14,17]. The objectives of this study were to determine if forest structural variables derived from ALS point clouds can be used to develop a predictive stand-level model of mean stem age for black spruce in the boreal forest of Ontario, and to improve upon previous approaches to modeling mean stem-level wood density by including both age and site quality variables as predictors.

2. Materials and Methods

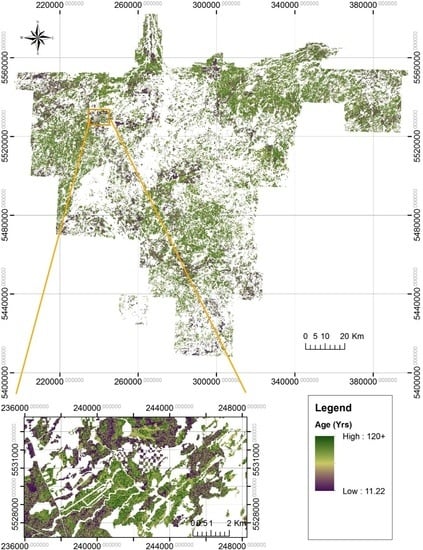
2.1. Study Area

The study was conducted in the Hearst Forest (HF) management unit (83°40′W, 49°40′N), one million hectares of productive forest land [18] within northeastern Ontario, Canada (Figure 1). The HF falls within the northern claybelt of the boreal forest region, which is typified by low-lying glaciolacustrine till, known for its poor drainage. The predominant topography is flat ground at low elevation (e.g., ≤86 m a.s.l.); however, there are some upland glaciofluvial landforms that reach elevations of up to 400 m [18,19]. The southern portion of the HF has sandy Humero-Ferric Podzols, with some bedrock outcrops. The northern portion has poor drainage and the soils are mostly Mesisols (24%) and Gleysols (18%) [20]. Black spruce (Picea mariana Mill. B.S.P.) is the most common tree species found in the HF, occurring across a broad range of conditions from dry uplands to wet lowlands [21]. Meteorological data from the weather station in Kapuskasing, ON, (49.3803°N, 82.4001°W) indicate that mean monthly air temperatures fall between −18.6 °C (January) and 17.2 °C (July). The yearly mean temperature is 1.3 °C and the average yearly precipitation is 838.8 mm [22]. Growth rates in the HF are limited by landscape level moisture and nutrient gradients, as well as a short number of frost-free days (92) during the summer months [18].

2.2. Sampling Design

In 2007, ALS data were acquired for the entire HF (1,231,707 ha). Northwest Geomatics LTD acquired the data during the leaf-on period between 4 July 2007 and 4 September 2007. The ALS sensor was a Leica ALS50 (Leica Geosystems, Heerbrugg, Switzerland) mounted on a Cessna 310 aircraft, with acquisition parameters that allowed for a 30° field of view with a 20% overlap [21]. The 11900 Hz pulse rate and 32 Hz scan rate produced an average point density of 0.82 points per square meter [23]. The raw point cloud data was summarized into structural predictor variables (Table 1) at the plot-level and over a 20 × 20 m raster of the HF, as described in [23]. In addition to these structural variables, a 20 × 20 m topographic wetness index (TWI) from ALS-derived elevation data was calculated following Bevin [24]. In 2010, a network of 446 circular 400 m2 (11.28 m radius) Temporary Sample Plots (TSPs) were established across the HF (Figure 2) in order to support a series of collaborative research projects [23].
The TSP locations were chosen using a stratification that represented the full geographical range of the HF as well as the entire range of stand development stages present in the forest. A comprehensive breakdown of this sampling design including descriptions of how all ALS variables were calculated can be found in Penner et al. [21]. In each plot, forest mensuration variables such as height (m) and diameter at breast height (DBH) (cm) were collected from all living trees ≥ 10 cm DBH [23]. An ecosite and substrate classification was designated for each plot based on information collected from a soil auger profile [23]. Classification of substrate and overstorey species cover was used to identify an ecosite classification according to the Ontario Ecological Land Classification Manual [25]. For this study, ecosites were grouped according to soil moisture regimes and textures. There were nine groups in total, describing site conditions from dry to hydric. Ecosite group 2 were dry sandy sites, ecosite group 3 were fresh, sandy or dry to fresh coarse loamy sites, ecosite group 4 were moist sandy to coarse loamy sites, ecosite group 5 were fresh clayey sites, ecosite group 6 were fresh silty to fine loamy sites, and ecosite group 7 were moist, silty to fine loamy to clayey sites. Ecosite group 8 (hydric or permanently flooded ecosites) was divided into three subcategories representing conifer swamps that were rich 8r, intermediate 8i, and poor 8p in nutrients.

2.3. Age Modeling

A subset of 134 TSPs was selected from the network to represent black spruce-dominated plots for the development of an age prediction model. Plots with ≥50% black spruce cover (basal area) were identified as spruce-dominated. A field campaign was initiated from December 2016 to August 2017 for the collection of a sample of approximately 10 increment cores from black spruce trees (DBH ≥10 cm) in each plot, which was expected to sufficiently capture the variation in age. This was similar to the sample size used by Racine et al. [2] to model stand-age in the boreal forest of Quebec. Increment core samples were mounted and sanded so that all annual rings were discernible using standard dendrochronological techniques [26,27]. Dating and counting of annual rings was done under an Olympus SZ61 bifocal microscope (Olympus Corporation, Tokyo, Japan) from 6.7–45× magnification. For increment cores that did not strike the pith, an estimate of the number of missing rings was made based on ring curvature following the method of Applequist [28], and ages were adjusted accordingly. For consistency, all individual tree ages were determined to 2007, when the ALS was flown.
Non-parametric approaches such as imputation methods using k nearest neighbor (kNN) classification derived from distances in multivariate space, are well suited to large ALS datasets of forest attributes [29], and have been successfully employed in age prediction for regular single cohort boreal forest stands [2]. A nonparametric, imputation approach allows a prediction to be made for a target observation based on the most similar reference observation within the data set [29]. Various methods of determining nearest neighbor reference observations can be employed. Random forests (rf) is a classification method [30] that can be used to generate a distance metric to apply kNN and impute predictions of a response variable across a landscape. Random forests distance is defined by Crookston et al. 2019 as (1–P), where P = the proportion of random forest trees where a target observation is in the same terminal node as a reference observation [31]. We conducted kNN with k = 1 and based on the random forests distance (hereafter referred to as rf-kNN) using the “YaImpute” package version 1.0–26 [31] in the R statistical computing environment version 3.4 [32]. YaImpute was created to deal with large numbers of predictor variables, and can be used to impute predictions as a raster output. For model variable selection, an automated recursive process was followed using the varselection function within YaImpute, which allowed predictors to be chosen that reduced the model’s error while still providing unique information. The variables chosen using this method were TWI, Elevation, cc16, P50, cc4, COVAR, cc10 and Max height. Model performance was assessed based on the root mean square difference (RMSD), which is a measure of the model error based on the differences between target and reference values, for all observations that have both [31]
Several subsets of the age dataset were examined to determine how model performance varied based on stand characteristics [33]. In mixed stands with weak dominance of black spruce the model produced poor age predictions. Thus, the final dataset was trimmed to include only plots that had greater than 70% black spruce (% basal area) and contained no hardwood or eastern white cedar (n = 116). The model also produced poor predictions in plots with a mean age greater than 120 years. Based on this trend and an analysis of the pattern of height changes as a function of age, an old growth age class was created for plots with mean ages ≥ 120 years to address this issue. A map layer depicting the area of the HF representing the stands described by the restrictions of the final age modeling dataset was generated from the FRI in ArcMap (version 10.1, ESRI, Redlands, CA, USA), and this map was linked to the raster of ALS-derived predictor variables for the same area. Stand age was imputed across the forest at the raster level (20 × 20 m pixel) using the YaImpute and the Asciigridimpute functions.

2.4. Wood Density Modeling

A total of 80 plots were selected from the 446 TSPs originally established in 2010 for collection of wood quality data. Large increment core samples (12 mm diameter) were collected from these plots over two field campaigns, conducted in 2011 and 2014. The approach taken with the wood density model was to predict an average tree level trait expected to occur within a given spatial area (in this case a 20 × 20 m raster pixel), which would allow users to identify portions of the landscape expected to contain trees with specific wood traits [4,9,34]. To facilitate this approach, it was important that the fitting dataset was composed of trees that were representative of the stands within which they occurred. The following criteria were used to identify cores that represented the average or typical tree for a given stand; cores were extracted only from co-dominant or dominant individuals, within ±10 centimeters of the mean diameter at breast height for the plot, and within 30 years of the mean plot age. Some of the plots in this study were within multiple cohort stands where a large range of ages and wood qualities were present. A mean wood density value from a single tree would not have adequately represented the wood density measurements across multiple cohorts at the plot level and therefore these plots were removed from the study. To use the imputed age from the rf-kNN analysis in the wood quality model, the dataset was further subset to match the conditions of that model, which meant removing plots that had less than 70% black spruce mixed with a component of hardwood or eastern white cedar. The final dataset was made up of 109 increment core samples from 80 plots that represented a range of ecosite groups. The majority of plots were classified as ecosite group 8i and 8p, comprising 70% of plots represented in this model.
Increment cores were sent to FPInnovations (Vancouver), where they were analyzed using SilviScan technology to obtain ring-level wood quality measurements [35,36]. Nominal density was measured at the ring-level using an X-ray densitometer at 25 μm resolution, 0.5 mm below the core surface. From the nominal density measurement, true density was calculated with a moisture content of 8% from volume and mass measurements that were calculated with micrometry.
Prior to fitting classification models, a preliminary list of potential predictor variables was developed based on the results of a stepwise multiple linear regression to prune the variable list using the “car” package [37] in R. To ensure the model was not over fit, variables were removed until all remaining had variance inflation factors less than 10. Regression tree analysis is a method for predicting values of a single response variable using a hierarchical classification tree to split the data into progressively homogenous groups. While regression trees are specific to the fitting data set, they can provide insights into the ecological drivers of the response variable [38]. We developed a regression tree of wood density from the list of predictors derived from the multiple linear regression (MLR), using the “rPart” Package [39] in R. The regression tree was pruned to cp ≤ 0.015. Random forests [40], a consensus-based modeling approach that can be used to provide a general simulation of hierarchical classification, was used to predict wood density over the range of conditions represented by the fitting data set. The final model was run with nine predictor variables, six derived from the ALS point cloud (cc4, cc6, cc12, VCI, D2, and P50) one derived from the forest resources inventory (ecosite group), one modeled from ALS data (QMDBH), and the final variable, age, derived from the rf-kNN model. A regression type model was conducted, with 8 variables tried at each split, a maximum of 4 nodes permitted and a total of 5000 trees created. To predict wood density across the entire set of spruce-dominated polygons in the HF, the subset of polygons that represented the same conditions used in the rf-kNN age model was identified, and the random forests simulation was computed across the entire area using the Modelmap package in R [41].

3. Results

3.1. Age Modeling

The sampling design captured a wide variation in age structure across the forest. The youngest plots were 8 years old at breast height, and the oldest were 160 years (Figure 3). The height structure of the plots varied with mean plot age, showing a clear decrease in height at the top (P90) and middle (P50) of the canopy at approximately 80 years (Figure 4). At 120 years there was a conspicuous increase in height of P90 and P50 (Figure 4). This notable increase in age complexity suggested a threshold beyond which the mean stem age could not be predicted. For this reason, a single age class was created for stands older than 120 years, which are hereafter referred to as 121+.
The predictor variables describing site conditions like elevation and TWI were the most important explanatory variables in the model (Figure 5). Variables that represent the complexity of the canopy at various heights (cc16, cc4, and cc10) and COVAR, which describes complexity as SD/mean, were also somewhat important for explaining age. This was expected since age is highly related to structural changes over time (Figure 4). The kNN age model using random forests as the special distance metric explained 62.87% of the variation of age in the sample population (Figure 6) and had a root mean square difference (RMSD) of 15 years. These are good results considering that many stands were from naturally regenerating origin and represented a large amount of structural and site condition variation across the landscape.
To demonstrate the application of this model at an operational scale, a map of predicted mean tree age was produced from the imputed age for all polygons in the FRI that met the rf-kNN variable criteria (Figure 7). Age variation can be very high, even within one FRI polygon. The map shows pockets of older stands in the northeastern portion of the HF where less road access is possible. The map insert, shows that areas that were recently harvested appear as young stands with a single cohort of trees displayed as purple patches on the map. It also shows that for the most part when older raster cells (121+ years) are present they are normally interspersed with medium aged raster cells (~80 years), which conveys the multicohort nature of these stands.

3.2. Wood Density Modeling

The dry sandy ecosite groups (EG2–EG4) had mean top heights greater than 19 m and were generally younger (64–80 years) (Table 2). The hydric sites had shorter, older trees with mean heights between 14–18 m and mean ages of 100–120 years (Table 2). Plots in ecosite group 8p, poor conifer swamps typified by poorly drained organic soil, had the highest mean density of 536 kg·m−3. In contrast, the mean density for samples in ecosite group 4, dry sandy to coarse loamy sites, were the lowest at 413.2 kg·m−3 (Table 2). The general trend was that ecosite groups that provided poorer growing conditions tended to have the highest wood density, whereas the faster growing, drier sites had the lowest wood density (Table 2).
There was a clear separation of density values across the nodes produced in the regression tree analysis (Figure 8). The regression tree model of wood density had a RMSE of 63.87 kg·m−3 and a coefficient of determination of 0.52. Age and ecosite were both important variables in the classification of wood density. The first split in the regression was based on ecosite groups, with EG 3–7 separating into a node where mean densities were typically low (~400–500 kg·m−3) (Figure 8). Mean density within the node containing the wet ecosites (EG-8i and 8p) was higher, with predictions ranging from 450–650 kg·m−3 (Figure 8). Other than the main division represented by ecosite differences, various other predictors formed nodes on the tree within these two branches. On wet ecosites, higher densities were predicted for sites with smaller canopy cover at 12 m and smaller QMDBH, and for sites with higher VCI. On dry ecosites, higher densities were predicted for sites with higher canopy closure at 6 m and higher ages. The lowest predicted density occurred for sites on EG 3–7, with canopy cover at 6 m less than 58%. The highest densities were predicted for sites on EG 8i and 8p, with canopy cover at 12 m less than 15% and QMDBH less than 11.91 cm. Although age was not directly selected in the nodes of the tree that included the wet sites, there was a strong correlation between age and VCI and QMDBH, which were selected variables on those nodes.
The most important variable extracted in the random forests simulation was ecosite group, which reduced mean squared error (MSE) by close to 50% when it was included in model fitting (Figure 9). Other important variables that reduced MSE substantially (5–35%) were the same variables that were elucidated in the regression tree analysis (e.g., cc6, cc12, age, QMDBH, and VCI) (Figure 9). The variables D2, P50, and cc4 entered the random forests model; however these all had minimal impacts on error when excluded from the model (Figure 9).
Overall the final random forests simulation for all 109 black spruce plots described 13.54% of the variation in the sample population with a RMSE of 59.31 kg·m−3 (Figure 10). Generally, the model tended to over-predict the plots with low wood density (400 kg·m−3) and under-predict plots with higher wood density (650 kg·m−3) (Figure 10).
The mean wood density map shows an example of how wood qualities could be mapped across the landscape based on a projection of the random forests simulations employed in this study (Figure 11). The insert shows a close-up view of a small section of forest that has recently experienced forest depletion through harvesting. There are clearly visible pockets of high (613 kg·m−3) and low density, which could be used for operational planning. The map indicates that clearly defined patches of wood with a relatively homogenous density can be found, as well as some places where there is a mixture of densities within the same area. This level of detail could also easily be averaged by polygon to show less variation as a more simplified tool for planning. Distinct areas of dense wood can be observed even at this low resolution. At the forest management unit level, patterns of wood density are visible such as the section of high density wood predicted in the northwest corner of the forest unit and patches of low density wood in the northeast section.

4. Discussion

4.1. Age Prediction

The final model we produced using the rf-kNN approach was useful for efficiently and accurately predicting the mean age of black spruce-dominated stands in boreal Ontario within 15 years, explaining 62.87% of the sample population variance. The random forests distance produced the best results, compared to two alternative Euclidian distance metrics also used in forest mensuration that were tried, most similar neighbor (MSN) and mahalanobis (MAL). These distance metrics produced poorer root mean square differences (RMSD) than random forests, at 23.9 years for MSN and 25.5 years for MAL. Our rf-kNN model results are comparable to those obtained by Racine et al. [2], who successfully applied the kNN approach with ALS-derived variables (e.g., Weibull curves, P95, first return penetration) as indicators of vertical forest structure and site characteristics to predict broad patterns of age in the boreal region of Québec, reporting slightly lower error (10 years), and higher explained variance (r2 = 0.84). The discrepancy in performance between these models was driven by the greater range of age and canopy structure in our fitting data from the HF. The mean age of plots in the Quebec study was 50 years, whereas it approached 90 years in the HF. Age is harder to predict in older stands, since patterns of stand dynamics have a greater chance of being influenced by small scale localized disturbances like wind-throw. Additionally, as multiple cohorts of different aged trees replace the initial cohort that emerged after a stand-replacing disturbance, the mean age can be influenced by individuals at either end of the distribution, making representative sampling difficult. It would therefore be expected that model performance would decline in a forest with an increasing proportion of old, multi-cohort stands. A study in Finland that used time series photographs to determine age since last stand replacing disturbance had an overall accuracy of classifying stand age of 78.9% [14]. However, their methodology limited estimations of age to areas with suitable aerial photograph coverage. Their results showed that older photographs had poorer prediction accuracies (before 1991) which is beyond the mean stand age (90+ years) in the HF. Maltamo et al. [42] used the k most similar neighbor (k-MSN) approach to predict common FRI attributes including mean tree age, and were able to predict age with similar error to our study, with an RMSE of 16 years for Norway spruce. The consistent problem in all of these studies has been in predicting the age of old growth stands where patterns of development are non-linear [14].
Examination of the pattern of P90 and P50 of ALS data in relation to mean tree age illustrated the changes in canopy complexity expected as stands develop under single species stand dynamics [12]. The stem re-initiation phase began at 80 years as indicated by a decrease in top height and mid-canopy height. At 120 years there was another clear increase in height for both P90 and P50, suggesting the beginning of the transition old growth phase. Multiple cohorts of trees in these transition old growth stands make it very difficult to predict a meaningful age, since the mean age of trees no longer describes the majority of the stand, but rather represents a mid-point of a broad range of ages. For the HF, this occurred in stands with a mean age of approximately 120 years, and therefore an age class was created that indicates these stands are generally multi-cohort, and should be considered as transitional or true old growth.
Age prediction accuracy in black spruce-dominated stands that had even a small proportion of eastern white cedar and birch or trembling aspen was poor. The rf-kNN method uses ecological neighbor stands with known ages to impute predictions. The model requires stand structures in the fitting data set that are similar to those being imputed in the main data set, in order to find appropriate neighbor matches. Since the canopy structure of eastern white cedar or hardwood trees is different than black spruce, and the number of plots with examples of these eastern white cedar/hardwood structures was low, there were not enough neighbors to appropriately match stands and make good predictions. Specifically, eastern white cedar has an ellipsoidal crown structure, whereas spruce are conical. Most of the foliage on hardwoods is in the upper canopy and the shape of their crowns is almost circular. The point cloud derived variables were created from low-density ALS data, therefore, the various crown structures could not be clearly differentiated. Instead, measurements of canopy height distribution (e.g., cc16, P50) provided the best options for differentiating stand structures as a function of age. For this reason, eastern white cedar or hardwood trees might have caused confusion in the model by increasing canopy closure metrics that are similar to a different age in spruce-dominated stands.
Topographic wetness index (TWI) was the most important predictor of mean stand age. The TWI describes the pooling and flow of water on the landscape [24], and was also found to be an important predictor for age in boreal stands of Quebec [2]. It is derived from the digital terrain model and depicts hydrological movement, however it is not a direct descriptor of soil moisture availability, since it does not account for variation in soil texture. Thus, TWI can only be used to generally indicate areas that may be affected by flooding (accumulation) or drought (dissipation). In areas where trees are stressed by flooding or drought conditions, growth rate is slow. Elevation was another important predictor of stand age. The terrain in the HF is mainly flat, and the substrates consist largely of heavier organic/clayey soils on the low, flat areas, with dry sandy soils restricted to the higher elevations. Although the differences in elevation among sites across the HF can be small, the effects of elevation change can be clearly observed in the variation of the ratio of height and age. Ultimately, the effects of TWI and elevation manifest as increased nutrient availability, better drainage and a slight increase in soil temperature that collectively increase growth rate in upland stands compared to the slow growth of stands in low-lying areas. Most of the black spruce-dominated stands in the HF were classified as slow-growing lowland conifer swamps. Previous studies have demonstrated that poorer sites have higher tree longevity and longer successional stages than more productive sites [43,44,45]. This is due in part to the rate at which trees reach maximum growth and senescence [44]. Additionally, since growth rate is linked to site conditions, it may also have driven some of the harvest patterns in the past, where the largest and easiest to access trees were harvested first [45], creating a pattern on the landscape such that slower-growing stands on wet sites are older.
Studies have shown that stand height is typically an important predictor of stand age [2,12,14,46,47]; however, it was not a key predictor of age in our study. The main reason for this apparent exception is the range of ages and stand structures we considered for this study. The sample population of 116 plots had a mean age of 90 years, and the scatter plot of canopy returns by age in these stands suggested that gap dynamics start to affect the age structure of plots around 80 years. Thus, a large proportion of plots in our study were likely influenced by multi-cohort stand dynamics. If we had restricted the model to apply to only the development of single cohorts, which our data suggested occurs up to approximately 80 years, then it is likely that height would have been more useful for predicting age. The changes in canopy structure that accompany this successional process can be characterized by examining the vertical distribution of foliage over multiple layers or height bins, and quantities that describe this change are often important predictors of age because they are linked to stand dynamics [12]. The vertical complexity index (VCI), applies Shannon’s equation to binned point cloud returns to capture the variation in vertical distribution of points in the point cloud [17]. Although VCI was entered as a predictor for our model, it had relatively low importance to model performance. Nevertheless, VCI was highly correlated to many of the variables that were important, including the canopy closure at various heights (cc16 and cc4) and P50 height. Thus, variables that describe vertical canopy structure were indeed useful predictors of stand age.
Ultimately, our model allowed for the prediction of a mean stand age with an error of approximately 15 years. It was necessary to truncate the predictions at 120 years, given the difficulties that arise when dealing with multi-cohort stands; however, this is justified because the complexity of old growth stands is effectively ignored when they are assigned a mean age. Perhaps a better approach in such stands would be to attempt to predict the ages of individual trees and then examine various properties of the distribution in addition to the mean. One way that the stand age map created in this study could be useful is by identifying stands that have been classified as old growth, facilitating the use of the age structure of the forest for natural disturbance emulation [48]. Imputing ages on a 20 × 20 m raster pixel scale creates the opportunity for forest managers to account for age variation within FRI polygons, and support better management of forest age structure. Ultimately, a higher density ALS point cloud would improve the estimation of the key forest structural variables. The low-resolution of the point cloud utilized for this study restricted age predictions to a plot level mean. Since there were only age measurements for ~10 trees per plot, error in the models was caused by matching point cloud statistics summarized for many trees at the plot level (including trees without age data) and the sample trees. Higher resolution point clouds and age information from all of the trees in a plot could make single tree age prediction models possible. A source of potential error in the rf-kNN model is a bias towards rare samples, since the dataset was found to be imbalanced in regards to plot age. In future studies, special attention should be paid to attaining a balanced sample distribution to avoid this bias.

4.2. Wood Density Modeling

The wood density models produced in this study have broadened the range of conditions under which wood density predictions can be made in the boreal forest of Ontario, by adding age as a potential predictor variable without substantially increasing error. The RMSE of our model that applies to stands up to 120 years in age was 59.1 kg·m−3, and compares well to previous studies in which the range of ages was restricted to the first 50 years of growth and RMSE values of 40.4 kg·m−3 [9] and 38.8 kg·m−3 [4] were reported. Furthermore, including age effects achieves an operational implementation goal to apply the model to black spruce-dominated polygons of all ages. There are still gains that could be made in accuracy that might be achieved with higher density ALS data. Blanchette et al. [49] developed a model from terrestrial laser scanning (TLS) data, which has a much higher point density (30 pulses/meter), and were able predict wood density more accurately (RMSE 23.87 kg·m−3) at a finer scale. The use of TLS, however, limits the generalizability of this type of predictive modeling, since it is currently only suitable for use over a small area (plot level), whereas ALS allows for less accurate but broader scale predictions to be made, which could be used in enhanced FRI’s.
Stand age was an important indicator of average wood density in both the regression tree and random forests analyses. Young trees have a large proportion of corewood typified by low density and short fibers [50,51]. In trees that have reached maturity, the density of wood stabilizes and therefore, older trees have a greater proportion of outerwood, which is of higher density. Understanding which logs have a higher proportion of high density wood, is useful for determining which trees are better suited for structural timber products like saw logs [10]. Additionally, there is an important interaction between stand age and site quality that clearly affects wood attributes such as density. In Ontario, ecosites are defined by substrate characteristics like soil type and texture, and moisture regime, which describe the availability of water across a landscape. In hydric sites like ecosite group 8i or 8p, pith to bark profiles reach a stable state with generally high density wood after the first few years of growth. This arises from a physiological response to consistently flooded conditions on these sites, and is caused by selective pressure for thicker cell walls to protect cells from embolism. Cell diameter is also reduced in the xylem of trees exposed to saturated conditions, which limits the risk of embolism when turgor pressure is low [52]. On the mesic sites represented by ecosite groups 3–7, pith to bark profiles tend to have greater variability of density in the first fifty years of growth [6,12]. Generally high density wood is found directly adjacent to the pith, then there is a steep decrease in density, followed by a gradual increase to a stable state within the first 30 to 50 years [6,12]. Drier sites tend to have less dense wood and more variability across the pith to bark profile than wetter sites. These common trends explain some of the descriptive power of ecosite group in the regression tree and random forests models. The interaction of age and ecosite that is captured in our model could have important consequences for operational application. For example, a mean density estimated for a typical tree on a dry to fresh site where the stable density is reached around 50 years, will become increasingly influenced by high density outerwood as the tree ages beyond 50. The effect would not be as important in trees on wet sites, which tend to have higher and more uniform density from pith to bark. For this reason, age may be a more important predictor on the dry or mesic sites, since young trees express this site-related variation in the pith-to-bark more strongly than older trees.
Forest structure also influences intrinsic wood qualities [7]. The ALS variables related to canopy closure and quadratic mean diameter were all found to be important in predicting wood density in our study. These metrics could be indicators of competition and light availability at the site level, which have been shown to have a negative relationship to wood density in shade tolerant species [53]. One reason for this negative correlation of wood density to variables that indicate a more open stand structure could be the role of high density wood with long fibers and thick cell walls as an anatomical response to wind, especially when there is low stocking density and trees are unprotected [12]. These metrics may also be indicators of average crown size, which would be related to stem structural strength required to support the higher load of a large crown, and would have a positive correlation to wood density [6,7,53]. Variation in density could also be affected by genetic variation within a species, which could account for some of the error in the model [54].
Predictive mapping is a useful way to link structurally explicit ALS data and site characteristics to show where specific wood qualities can be found in the forest. The wood density map created for this project for example, could be used to display areas where there are pockets of wood with predicted density greater than or less than a specific value. These pockets would be described by combinations of age and ecosite; therefore, the performance of the model could be constrained by the reliability of interpretations of ecosites in the FRI. Nevertheless, this approach could be useful for supporting decisions about products with specification thresholds for raw materials (e.g., density ≥ 500 kg·m−3). Enhanced forest inventories with wood quality variables that are not normally included could allow for the industry to be responsive to market demands that are constantly changing and support value chain optimization [55].

5. Conclusions

The non-parametric rf-kNN model of forest stand age developed for black spruce stands in the boreal forest of Ontario from ALS structural information was useful for imputing accurate age estimates, which could be subsequently included as a derived variable in a given FRI system. This type of indirect predictive modeling of age creates estimates that can be obtained efficiently and consistently, given that the technique applies the same rules to the entire land base. An age map derived from the model could be used on an operational scale for a number of applications, including forest management planning or other predictive modeling projects that require mean forest age. Predictive modeling of wood quality attributes, using the derived age imputed from the rf-kNN approach, allowed for the expanded application of a model of mean wood density using a random forests approach. Descriptive wood quality maps can be developed from random forests simulations and used as planning tools to optimize the value chain of forest timber harvesting by selecting specific wood qualities to target prior to harvest. The efficiency with which wood density can be calculated from ALS data creates the opportunity for enhanced forest inventories to be more reactive to economic demands that are difficult to react to when they are based on more traditional FRI methods.

Author Contributions

Conceptualization, J.P.D. and R.R.M.W.; data curation, M.E.W.; methodology, R.R.M.W., J.P.D. and M.E.W.; formal analysis, R.R.M.W.; investigation, R.R.M.W.; resources, J.P.D. and M.E.W.; writing—original draft preparation, R.R.M.W.; writing—review and editing, J.P.D. and M.W.; project administration, J.P.D.; funding acquisition, J.P.D.

Funding

This research was supported by the AWARE project (NSERC File: CRDPJ 462973 – 14, Grantee: N.C. Coops, FRM, UBC), in collaboration with Canadian Wood Fiber Centre (CWFC), FP-Innovations and Hearst Forest Management Inc.

Acknowledgments

The authors thank Thunderhouse Forest Service for support in data collection as well as John Kovacs and Adam Dick for reviewing a version of this study and providing helpful comments.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Treitz, P.; Lim, K.; Woods, M.; Pitt, D.; Nesbitt, D.; Etheridge, D. LiDAR sampling density for forest resource inventories in Ontario, Canada. Remote Sens. 2012, 4, 830–848. [Google Scholar] [CrossRef]
  2. Racine, E.B.; Coops, N.C.; St-Onge, B.; Begin, J. Forest stand age from LiDAR—Derived predictors and nearest neighbor imputation. For. Sci. 2014, 60, 128–136. [Google Scholar] [CrossRef]
  3. Luther, J.E.; Skinner, R.; Fournier, R.A.; van Lier, O.R.; Bowers, W.W.; Cote, J.-F.; Hopkinson, C.; Moulton, T. Predicting wood quantity and quality attributes of balsam fir and black spruce using airborne laser scanner data. Forestry 2013, 87, 1–14. [Google Scholar] [CrossRef]
  4. Pokharel, B.; Groot, A.; Pitt, D.G.; Woods, M.; Dech, J.P. Predictive modeling of Black Spruce (Picea mariana (Mill.) B.S.P) wood density using stand structure variables derived from airborne LiDAR data in Boreal forests of Ontario. Forests 2016, 7, 311. [Google Scholar] [CrossRef]
  5. Pitt, D.; Pineau, J. Forest inventory research at the Canadian wood fibre centre: Notes from a research coordination workshop, June 3–4, 2009, Pointe Claire, QC. For. Chron. 2009, 85, 859–869. [Google Scholar] [CrossRef]
  6. Carlquist, S. How wood evolves: A new synthesis. Botany 2012, 90, 901–940. [Google Scholar] [CrossRef]
  7. Van Leeuwen, M.; Hilker, T.; Coops, N.C.; Frazer, G.; Wulder, M.A.; Newnham, G.J.; Culvenor, D.S. Assessment of standing wood and fibre quality using ground and airborne laser scanning: A review. For. Ecol. Manag. 2011, 261, 1467–1478. [Google Scholar] [CrossRef]
  8. Jozsa, L.; Middleton, G. A Discussion of Wood Quality Attributes and Their Practical Implications; Forintek Canada Corp.: Vancouver, BC, Canada, 1994. [Google Scholar]
  9. Pokharel, B.; Dech, J.P.; Groot, A.; Pitt, D. Ecosite-based predictive modeling of black spruce (Picea mariana) wood quality attributes in Boreal Ontario. Can. J. For. Res. 2014, 44, 465–475. [Google Scholar] [CrossRef]
  10. Lachenbruch, B.; Moore, J.R.; Evans, R. Radial Variation in Wood Structure and Function in Woody Plants, and Hypotheses for Its Occurrence in Size—And Age—Related Changes in Tree Structure and Function; Meinzer, F.C., Lachenbruch, B., Eds.; Springer: New York, NY, USA, 2011. [Google Scholar]
  11. Gartner, B.L.; Stoke, D.; Groom, L.H. Prediction of wood structural patterns in trees by using ecological models of plant water relations. In Characterization of the Cellulosic Cell Wall; Blackwell Publishing: Hoboken, NJ, USA, 2006. [Google Scholar]
  12. Oliver, C.D.; Larson, B.C. Forest Stand Dynamics; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
  13. Ung, C.H.; Bernier, P.Y.; Raulier, F.; Fournier, R.A.; Lambert, M.C.; ReGinere, J. Biophysical site indices for shade tolerant and intolerant boreal species. For. Sci. 2001, 47, 85–95. [Google Scholar]
  14. Vastaranta, M.; Niemi, M.; Wulder, M.A.; White, J.C.; Nurminen, K.; Litkey, P.; Honkavaara, E.; Holopainen, M.; Hyyppä, J. Forest stand age classification using time series of photogrammetrically derived digital surface models. Scand. J. For. Res. 2015, 31, 194–205. [Google Scholar] [CrossRef] [Green Version]
  15. Van Pelt, R.; Nadkarni, N.M. Development of canopy structure in Pseudotsuga menziesii forest in southern Washington Cascades. For. Sci. 2004, 50, 326–341. [Google Scholar]
  16. Kane, V.R.; McGaughey, R.J.; Bakker, J.D.; Gersonde, R.F.; Lutz, J.A.; Franklin, J.F. Comparisons between field- and LiDAR-based measures of stand structural complexity. Can. J. For. Res. 2010, 40, 761–773. [Google Scholar] [CrossRef]
  17. Van Ewijk, K.; Treitz, P.; Scott, N. Characterizing forest succession in central Ontario using LiDAR derived indicies. Photogramm. Eng. Remote Sensing 2011, 77, 261–270. [Google Scholar] [CrossRef]
  18. Ekstorm, B.; Desneiges, L. Contingency Plan for Hearst Forest 2017–2019; MNRF: Hearst, ON, USA, 2017. [Google Scholar]
  19. Rowe, J.S. Forest Regions of Canada; Fisheries and Environment Canada, Canadian Forestry Service: Ottawa, ON, Canada, 1972; Volume 1300. [Google Scholar]
  20. Crins, W.J.; Gray, P.A.; Uhlig, W.C.; Wester, M.C. The Ecosystems of Ontario, Part I: Ecozones and Ecoregions Inventory, Monitoring and Assessment; Ministry of Natural Resources and Forestry: Peterborough, ON, Canada, 2009; p. 71. [Google Scholar]
  21. Penner, M.; Pitt, D.G.; Woods, M. Parametric vs. nonparametric LiDAR models for operational forest inventory in Boreal Ontario. Can. J. Remote Sens. 2013, 39, 426–443. [Google Scholar]
  22. Environment Canada. Canadian Climate Normals Between 1991–2010. Environment Canada Kapuskasing 2017. Available online: http://climate.weather.gc.ca/climate_normals/ (accessed on 26 August 2019).
  23. Woods, M.; Pitt, D.; Penner, M.; Lim, K.; Nesbitt, D.; Etheridge, D.; Treitz, P. Optimal implementation of an inventory in Boreal Ontario. For. Chron. 2011, 87, 512–528. [Google Scholar] [CrossRef]
  24. Bevin, K.J. Rainfall-Runoff Modelling; John Wiley and Sons: West Sussex, UK, 2001. [Google Scholar]
  25. Wester, M.; Uhlig, P.; Bakowsky, W.; Banton, E. Great Lakes—St Lawrence Ecosite Fact Sheets; Ontario Forest Research Institute: Sault Ste. Marie, ON, Canada, 2015. [Google Scholar]
  26. Stokes, A.M.; Smiley, T.L. An Introduction to Tree Ring Dating; University of Arizona Press: Tucson, AZ, USA, 1958. [Google Scholar]
  27. Speer, J.H. Fundamentals of Tree Ring Research; University of Arizona Press: Tucson, AZ, USA, 2010. [Google Scholar]
  28. Applequist, M.B. A simple pith locator for use with off centre increment cores. J. For. 1958, 56, 141. [Google Scholar]
  29. Hudak, A.T.; Crookston, N.L.; Evans, J.S.; Hall, D.E.; Falkowski, M.J. Nearest neighbor imputation of species-level, plot-scale forest structure attributes from LiDAR data. Remote Sens. Environ. 2008, 112, 2232–2245. [Google Scholar] [CrossRef] [Green Version]
  30. Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
  31. Crookston, N.L.; Finley, A.O. Yaimpute: An R package for k-NN imputation. J. Stat. Softw. 2008, 23, 1–16. [Google Scholar] [CrossRef]
  32. The R Project for Statistical Computing. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017; Available online: https://www.R-project.org (accessed on 27 August 2019).
  33. Wylie, R.R.M. Estimating Stand Age from Airborne Laser Scanning Data to Improve Ecosite-Based Models of Black Spruce Wood Density in the Boreal Forest of Ontario. MSc. Thesis, Nipissing University, North Bay, ON, Canada, 2019. [Google Scholar]
  34. Townsend, E.; Pokharel, B.; Groot, A.; Pitt, D.; Dech, J.P. Modeling wood fibre in black spruce (Picea mariana (mill.) BSP) based on ecological land classification. Forests 2015, 6, 3369–3394. [Google Scholar] [CrossRef]
  35. Defo, M.; Uy, N. SilviScan Analysis of Black Spruce, Jack Pine, and Trembling Aspen Samples; FPInnovations: Vancouver, BC, Canada, 2012. [Google Scholar]
  36. Tong, T. Silviscan Analysis of 96 Black Spruce Samples; FPInnovations: Vancouver, BC, Canada, 2015. [Google Scholar]
  37. Fox, J.; Weisberg, S. An R Companion to Applied Regression, 2nd ed.; Sage: Thousand Oaks, CA, USA, 2011. [Google Scholar]
  38. De’ath, G.; Fabricius, K.E. Classification and regression trees: A powerful yet simple technique for ecological data analysis. Ecology 2000, 81, 3178–3190. [Google Scholar] [CrossRef]
  39. Therneau, T.M.; Atkinson, B.; Ripley, B. Rpart: Recursive Partitioning. R Package Version 4.1-1. CRAN University of Toronto. Available online: https://cran.r-project.org/web/packages/rpart/index.html (accessed on 12 October 2018).
  40. Breiman, L.; Cutler, A.; Liaw, A.; Wiener, M. Random Forest: Breiman and Cutler’s Random Forests for Classificarion and Regression. R Package Version 4.6-7. CRAN University of Toronto. Available online: https://cran.r-project.org/web/packages/rpart/index.html (accessed on 25 May 2018).
  41. Freeman, E.; Frescino, T. ModelMap: Modelling and Map Production Using Random Forests and Stochastic Gradient Boosting; USDA Forest Service: Ogden, UT, USA, 2009.
  42. Maltamo, M.; Malinen, J.; Pakaln, P.; Suvanto, A.; Kangas, J. Nonparametric estimation of stem volume using airborne laser scanning, aerial photography and stand-register data. Can. J. For. Res. 2006, 36, 426–436. [Google Scholar] [CrossRef]
  43. Laberge, M.-J.; Payette, S.; Bousquet, J. Life span and biomass allocation of stunted black spruce clones in the subarctic environment. J. Ecol. 2000, 88, 584–593. [Google Scholar] [CrossRef]
  44. Boucher, D.; Gauthier, S.; De Grandpre, L. Structural changes in coniferous stands along a chronosequence and a productivity gradient in the northeastern boreal forest of Québec. Ecoscience 2006, 13, 172–180. [Google Scholar] [CrossRef]
  45. Boucher, D.; De Grandpre’, L.; Kneeshaw, D.; St Onge, B.; Ruel, J.-C.; Waldron, K.; Lussier, J.-M. Effects of 80 years of forest management on landscape structure and pattern in the eastern Canadian boreal forest. Landsc. Ecol. 2015, 30, 1913–1929. [Google Scholar] [CrossRef]
  46. Yang, Y.; Huang, S. Estimating a multilevel dominant height–age model from nested data, with generalized errors. For. Sci. 2011, 54, 102–116. [Google Scholar]
  47. Subedi, N.; Sharma, M.V. Evaluating height–age determination methods for jack pine and black spruce plantations using stem analysis data. North. J. Appl. For. 2010, 27, 50–55. [Google Scholar] [CrossRef]
  48. Harvey, B.D.; Leduc, A.; Gauthier, S.; Bergeron, Y. Stand-landscape integration in natural disturbance-based management of the southern boreal forest. For. Ecol. Manag. 2002, 155, 369–385. [Google Scholar] [CrossRef]
  49. Blanchette, D.; Fournier, R.A.; Luther, J.E.; Cote, J.-F. Predicting wood fibre attributes using local-scale metrics from terrestrial LiDAR data: A case study of newfoundland conifer species. For. Ecol. Manag. 2015, 347, 116–129. [Google Scholar] [CrossRef]
  50. Plomion, C.; Leprovost, G.; Stokes, A.M. Wood formation in trees. Plan. Physiol. 2001, 127, 1513–1523. [Google Scholar] [CrossRef]
  51. Zhang, S.Y. Wood quality attributes and their impacts on wood utilization. In Proceedings of the XII World Forestry Congress, Québec, QC, Canada, 21–28 September 2003; pp. 21–28. [Google Scholar]
  52. Marchand, P.J. Apparent ecotypic differences in water relations of some northern bog ericaceae. J. N. Engl. Bot. Club 1975, 77, 53–61. [Google Scholar]
  53. Janse-Ten Klooster, S.J.; Thomas, J.P.; Sterck, F.J. Explaining interspecific differences in sapling growth and shade tolerance in temperate forests. J. Ecol. 2007, 95, 1250–1260. [Google Scholar] [CrossRef]
  54. Savva, Y.; Koubaa, A.; Tremblay, F.; Bergeron, Y. Effects of radial growth, tree age, climate, and seed origin on wood density of diverse jack pine populations. Trees 2010, 24, 53–65. [Google Scholar] [CrossRef]
  55. Alam, B.; Shahi, C.; Pulkki, R. Economic impact of enhanced forest inventory information and merchandizing yards in the forest product industry supply chain. Soc. Econ. Plan. Sci. 2014, 48, 189–197. [Google Scholar] [CrossRef]
Remotesensing 11 02022 g001 550
Figure 1. Location of the Hearst Forest management unit within the province of Ontario.
Figure 1. Location of the Hearst Forest management unit within the province of Ontario.
Remotesensing 11 02022 g001
Remotesensing 11 02022 g002 550
Figure 2. Map of Hearst Forest, with the location of the plots, wood quality project (n = 80), and age prediction model (n = 116).
Figure 2. Map of Hearst Forest, with the location of the plots, wood quality project (n = 80), and age prediction model (n = 116).
Remotesensing 11 02022 g002
Remotesensing 11 02022 g003 550
Figure 3. Distribution for final age dataset with mean indicated by red dashed line, (a) the number of trees available per plot n = 116; (b) age distribution of all trees independent of plot n = 1277; (c) mean plot age n = 116; (d) standard deviation of plot age n = 116.
Figure 3. Distribution for final age dataset with mean indicated by red dashed line, (a) the number of trees available per plot n = 116; (b) age distribution of all trees independent of plot n = 1277; (c) mean plot age n = 116; (d) standard deviation of plot age n = 116.
Remotesensing 11 02022 g003
Remotesensing 11 02022 g004 550
Figure 4. Scatter plot of ALS fifth (P50) in orange and ninth (P90) in turquoise decile height (metres) at plot ages (years) shaded grey is 95% confidence interval. LOESS curves are fit to the distributions.
Figure 4. Scatter plot of ALS fifth (P50) in orange and ninth (P90) in turquoise decile height (metres) at plot ages (years) shaded grey is 95% confidence interval. LOESS curves are fit to the distributions.
Remotesensing 11 02022 g004
Remotesensing 11 02022 g005 550
Figure 5. Scaled variable importance for rf-kNN age prediction model of 116 black spruce-dominated plots in the Hearst Forest of Northeastern Ontario.
Figure 5. Scaled variable importance for rf-kNN age prediction model of 116 black spruce-dominated plots in the Hearst Forest of Northeastern Ontario.
Remotesensing 11 02022 g005
Remotesensing 11 02022 g006 550
Figure 6. Scatterplot of imputed vs. observed plot age for 116 black spruce-dominated plots in the Hearst Forest of Northeastern Ontario. Red line indicates a 1:1 ratio.
Figure 6. Scatterplot of imputed vs. observed plot age for 116 black spruce-dominated plots in the Hearst Forest of Northeastern Ontario. Red line indicates a 1:1 ratio.
Remotesensing 11 02022 g006
Remotesensing 11 02022 g007 550
Figure 7. Mean age (years) imputation for FRI polygons that met rf-kNN model requirements, using ALS structural metrics (MAX, cc4, cc10, cc16, P50, COVAR, Elevation and TWI) Hearst Forest in Northeastern Ontario.
Figure 7. Mean age (years) imputation for FRI polygons that met rf-kNN model requirements, using ALS structural metrics (MAX, cc4, cc10, cc16, P50, COVAR, Elevation and TWI) Hearst Forest in Northeastern Ontario.
Remotesensing 11 02022 g007
Remotesensing 11 02022 g008 550
Figure 8. Regression tree analysis of mean wood density (kg·m−3) of black spruce increment core samples collected between 2011 and 2014 from the Hearst Forest management unit in Northeastern Ontario (n = 109). The top figure illustrates the decision tree derived from the analysis, the boxplots illustrate the range of predicted values within the nodes of the tree. Predictors included ALS structural variables canopy closure at 6 and 12 m (cc12 and cc6), Quadratic mean diameter at breast height (QMDBH), vertical complexity index (VCI), and FRI-derived ecosite classifications (a = Fresh sandy and dry to fresh coarse loamy, b = moist sandy to coarse loamy, c = fresh clayey, d = fresh silty to fine loamy, e = intermediate conifer swamp, f = poor conifer swamp) and age derived directly from core samples.
Figure 8. Regression tree analysis of mean wood density (kg·m−3) of black spruce increment core samples collected between 2011 and 2014 from the Hearst Forest management unit in Northeastern Ontario (n = 109). The top figure illustrates the decision tree derived from the analysis, the boxplots illustrate the range of predicted values within the nodes of the tree. Predictors included ALS structural variables canopy closure at 6 and 12 m (cc12 and cc6), Quadratic mean diameter at breast height (QMDBH), vertical complexity index (VCI), and FRI-derived ecosite classifications (a = Fresh sandy and dry to fresh coarse loamy, b = moist sandy to coarse loamy, c = fresh clayey, d = fresh silty to fine loamy, e = intermediate conifer swamp, f = poor conifer swamp) and age derived directly from core samples.
Remotesensing 11 02022 g008
Remotesensing 11 02022 g009 550
Figure 9. Variable importance as a percentage increase in mean squared error (MSE) for random forests model predicting mean density (kg·m−3) for black spruce increment core samples in the Hearst Forest (n = 109).
Figure 9. Variable importance as a percentage increase in mean squared error (MSE) for random forests model predicting mean density (kg·m−3) for black spruce increment core samples in the Hearst Forest (n = 109).
Remotesensing 11 02022 g009
Remotesensing 11 02022 g010 550
Figure 10. Predicted vs. actual values of wood density (kg·m−3) for random forests model of black spruce wood density for the Hearst Forest of Northeastern Ontario (n = 109). The dashed red line is the line of best fit through the distribution.
Figure 10. Predicted vs. actual values of wood density (kg·m−3) for random forests model of black spruce wood density for the Hearst Forest of Northeastern Ontario (n = 109). The dashed red line is the line of best fit through the distribution.
Remotesensing 11 02022 g010
Remotesensing 11 02022 g011 550
Figure 11. Mean stem level wood density (kg·m−3) 20 × 20 m pixel, Hearst Forest Northeastern Ontario.
Figure 11. Mean stem level wood density (kg·m−3) 20 × 20 m pixel, Hearst Forest Northeastern Ontario.
Remotesensing 11 02022 g011
Table
Table 1. Complete list and description of predictor variables derived from ALS point cloud from which a smaller subset was selected for fitting final models.
Table 1. Complete list and description of predictor variables derived from ALS point cloud from which a smaller subset was selected for fitting final models.
ALS VariableDescription
MEAN_HMean Height (m)
STD_DEVStandard deviation of height (m)
ABS_DEVAbsolute deviation of height (m)
SKEWSkewness
KURTOSISKurtosis
MINMinimum height (m)
P10–P90First–ninth decile ALS height (m)
MAXMaximum height (m)
D1-D9Cumulative percentage of the numbers of binned returns
DAFirst returns/all returns
DBFirst and only return/all returns
DVFirst vegetation returns/all returns
MEDIAN_HMedian height (m)
VDRVertical Distribution Ratio = [MAX − Median]/MAX
COVARCovariance (STD/Mean)
CanCOVARCovariance (STD/Mean) of first returns only
SWIShannon-Weaver Index
VCIVertical Complexity Index (based on a 1m raster analysis)
FIRSTNumber of First Returns
ALLRETURNSNumber of all returns
FIRSTVEGNumber of first Vegetation Returns only
ALLGROUNDNumber of ground Returns
cc0–cc24Crown closure at 2 m increments (cc2 = crown closure between 2 and 4 m)
QMDBHQuadratic mean diameter at breast height (trees greater than 9 cm DBH)
Elevation (5 m)Elevation (m) (Derived from 5 m DTM
TWITopographic Wetness Index (Derived From 5 m DTM)
AspectAspect (°) (Derived from 5 m DTM)
SlopeSlope (°) (Derived from 5 m DTM)
Table
Table 2. Summary statistics for wood density and stand characteristics by ecosite groups in black spruce-dominated plots in the Hearst Forest in Northeastern Ontario.
Table 2. Summary statistics for wood density and stand characteristics by ecosite groups in black spruce-dominated plots in the Hearst Forest in Northeastern Ontario.
Ecosite Group n DBHHt.BAAgeSD AgeDens.
(cm)(m)(m2·ha−1)(yrs)(yrs)kg·m−3
Fresh Sandy/Dry-fresh coarse loamy EG3616.918.934.487427469.77
Moist Sandy to Coarse Loamy EG4219.319.730.05852413.21
Fresh Clayey EG51415.816.223.467636487.00
Fresh Silty to Fine Loamy EG6717.318.632.279227468.53
Fresh Silty to Fine Loamy to Clayey EG71218.217.327.617530493.61
Intermediate conifer swamp EG8i2515.115.320.7310827526.35
Poor Conifer swamp EG8p4315.915.724.0311028536.19
Overall 10916.216.324.819732469.77

Share and Cite

MDPI and ACS Style

Wylie, R.R.M.; Woods, M.E.; Dech, J.P. Estimating Stand Age from Airborne Laser Scanning Data to Improve Models of Black Spruce Wood Density in the Boreal Forest of Ontario. Remote Sens. 2019, 11, 2022. https://doi.org/10.3390/rs11172022

AMA Style

Wylie RRM, Woods ME, Dech JP. Estimating Stand Age from Airborne Laser Scanning Data to Improve Models of Black Spruce Wood Density in the Boreal Forest of Ontario. Remote Sensing. 2019; 11(17):2022. https://doi.org/10.3390/rs11172022

Chicago/Turabian Style

Wylie, Rebecca R.M., Murray E Woods, and Jeffery P. Dech. 2019. "Estimating Stand Age from Airborne Laser Scanning Data to Improve Models of Black Spruce Wood Density in the Boreal Forest of Ontario" Remote Sensing 11, no. 17: 2022. https://doi.org/10.3390/rs11172022

APA Style

Wylie, R. R. M., Woods, M. E., & Dech, J. P. (2019). Estimating Stand Age from Airborne Laser Scanning Data to Improve Models of Black Spruce Wood Density in the Boreal Forest of Ontario. Remote Sensing, 11(17), 2022. https://doi.org/10.3390/rs11172022

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop