Spectral and Radiometric Calibration of the Next Generation Airborne Visible Infrared Spectrometer (AVIRIS-NG)
Abstract
:1. Introduction
Instrument
2. Materials and Methods
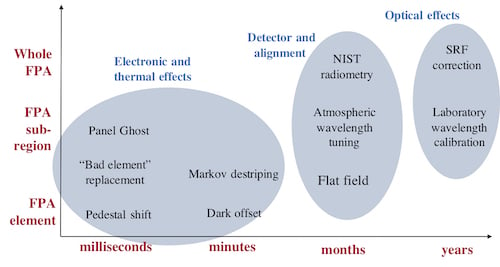
2.1. Algorithmic Approach
2.2. Radiometric Calibration
2.3. Markov Field Destriping
2.4. Atmospheric Wavelength Calibration
2.5. Statistical Bad Pixel Replacement
2.6. Scene Invariances as Point Spread Function Calibration Standards
2.7. Response Function Model
Estimating SRF from Flight Data
2.8. Geometric Processing
2.9. Laboratory and Field Protocols
2.10. Evaluation on Historical Data
3. Results
3.1. Flat Field Calibration
3.2. Radiometric Calibration
3.3. Image Destriping
3.4. Wavelength Calibration
4. Discussions
Future Directions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Thompson, D.R.; Guanter, L.; Berk, A.; Gao, B.C.; Richter, R.; Schläpfer, D.; Thome, K.J. Retrieval of Atmospheric Parameters and Surface Reflectance from Visible and Shortwave Infrared Imaging Spectroscopy Data. Surv. Geophys. 2018, 40, 333–360. [Google Scholar] [CrossRef] [Green Version]
- Thompson, D.R.; Boardman, J.W.; Eastwood, M.L.; Green, R.O.; Haag, J.M.; Mouroulis, P.; Van Gorp, B. Imaging spectrometer stray spectral response: In-flight characterization, correction, and validation. Remote. Sens. Environ. 2018, 204, 850–860. [Google Scholar] [CrossRef]
- Green, R.O.; Eastwood, M.L.; Sarture, C.M.; Chrien, T.G.; Aronsson, M.; Chippendale, B.J.; Faust, J.A.; Pavri, B.E.; Chovit, C.J.; Solis, M.; et al. Imaging Spectroscopy and the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Remote. Sens. Environ. 1998, 65, 227–248. [Google Scholar] [CrossRef]
- Mouroulis, P.; Green, R.O.; Van Gorp, B.; Moore, L.B.; Wilson, D.W.; Bender, H.A. Landsat swath imaging spectrometer design. Opt. Eng. 2016, 55, 015104. [Google Scholar] [CrossRef]
- Thompson, D.R.; Gao, B.C.; Green, R.O.; Roberts, D.A.; Dennison, P.E.; Lundeen, S.R. Atmospheric correction for global mapping spectroscopy: ATREM advances for the HyspIRI preparatory campaign. Remote. Sens. Environ. 2015, 167, 64–77. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Zong, Y.; Brown, S.W.; Johnson, B.C.; Lykke, K.R.; Ohno, Y. Simple spectral stray light correction method for array spectroradiometers. Appl. Opt. 2006, 45, 1111–1119. [Google Scholar] [CrossRef] [PubMed]
- Haag, J.M.; Van Gorp, B.E.; Mouroulis, P.; Thompson, D.R. Radiometric and spectral stray light correction for the portable remote imaging spectrometer (PRISM) coastal ocean sensor. In Proceedings of the Earth Observing Systems XXII, San Diego, CA, USA, 6–10 August 2017; SPIE: Bellingham, WA, USA, 2017; Volume 10402, p. 104020E. [Google Scholar] [CrossRef]
- Guanter, L.; Segl, K.; Sang, B.; Alonso, L.; Kaufmann, H.; Moreno, J. Scene-based spectral calibration assessment of high spectral resolution imaging spectrometers. Opt. Express 2009, 17, 11594–11606. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuhlmann, G.; Hueni, A.; Damm, A.; Brunner, D. An Algorithm for In-Flight Spectral Calibration of Imaging Spectrometers. Remote. Sens. 2016, 8, 1017. [Google Scholar] [CrossRef]
- Richter, R.; Schlapfer, D.; Muller, A. Operational Atmospheric Correction for Imaging Spectrometers Accounting for the Smile Effect. IEEE Trans. Geosci. Remote. Sens. 2011, 49, 1772–1780. [Google Scholar] [CrossRef]
- Boardman, J.W. Precision geocoding of low altitude AVIRIS data: Lessons learned in 1998. In eAVIRIS 1999 Proceedings; Jet Propulsion Laboratory: La Cañada Flintridge, CA, USA, 1999; pp. 63–68. [Google Scholar]
- Thompson, D.R.; Leifer, I.; Bovensmann, H.; Eastwood, M.; Fladeland, M.; Frankenberg, C.; Gerilowski, K.; Green, R.O.; Kratwurst, S.; Krings, T.; et al. Real-time remote detection and measurement for airborne imaging spectroscopy: A case study with methane. Atmos. Meas. Tech. 2015, 8, 4383–4397. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B. Revised landsat-5 tm radiometric calibration procedures and postcalibration dynamic ranges. IEEE Trans. Geosci. Remote. Sens. 2003, 41, 2674–2677. [Google Scholar] [CrossRef] [Green Version]
- Czapla-Myers, J.S.; Anderson, N.J. Post-Launch Radiometric Validation of the GOES-16 Advanced Baseline Imager (ABI). In Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2018; Volume 10785, p. 107851F. [Google Scholar] [CrossRef]
- Hook, S.J.; Myers, J.J.; Thome, K.J.; Fitzgerald, M.; Kahle, A.B. The MODIS/ASTER airborne simulator (MASTER) a new instrument for earth science studies. Remote. Sens. Environ. 2001, 76, 93–102. [Google Scholar] [CrossRef]
- Jablonski, J.; Durell, C.; Slonecker, T.; Wong, K.; Simon, B.; Eichelberger, A.; Osterberg, J. Best Practices in Passive Remote Sensing VNIR Hyperspectral System Hardware Calibrations. In Hyperspectral Imaging Sensors: Innovative Applications and Sensor Standards 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9860, p. 986004. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP Spaceborne Imaging Spectroscopy Mission for Earth Observation. Remote. Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef] [Green Version]
- Baumgartner, A.; Gege, P.; Köhler, C.; Lenhard, K.; Schwarzmaier, T. Characterisation methods for the hyperspectral sensor HySpex at DLR’s calibration home base. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XVI, Edinburgh, UK, 24–27 September 2012; International Society for Optics and Photonics: Bellingham, WA, USA, 2012; Volume 8533, p. 85331H. [Google Scholar]
- Fox, N.P. Trap Detectors and their Properties. Metrologia 1991, 28, 197–202. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific Publishing Co.: Singapore, 2000. [Google Scholar]
- Schultz, K.; Kelly, M.W.; Blackwell, M.H.; Brown, M.G.; Colonero, C.B. Digital-pixel focal plane array technology. Linc. Lab. J. 2014, 20, 36–51. [Google Scholar]











© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chapman, J.W.; Thompson, D.R.; Helmlinger, M.C.; Bue, B.D.; Green, R.O.; Eastwood, M.L.; Geier, S.; Olson-Duvall, W.; Lundeen, S.R. Spectral and Radiometric Calibration of the Next Generation Airborne Visible Infrared Spectrometer (AVIRIS-NG). Remote Sens. 2019, 11, 2129. https://doi.org/10.3390/rs11182129
Chapman JW, Thompson DR, Helmlinger MC, Bue BD, Green RO, Eastwood ML, Geier S, Olson-Duvall W, Lundeen SR. Spectral and Radiometric Calibration of the Next Generation Airborne Visible Infrared Spectrometer (AVIRIS-NG). Remote Sensing. 2019; 11(18):2129. https://doi.org/10.3390/rs11182129
Chicago/Turabian StyleChapman, John W., David R. Thompson, Mark C. Helmlinger, Brian D. Bue, Robert O. Green, Michael L. Eastwood, Sven Geier, Winston Olson-Duvall, and Sarah R. Lundeen. 2019. "Spectral and Radiometric Calibration of the Next Generation Airborne Visible Infrared Spectrometer (AVIRIS-NG)" Remote Sensing 11, no. 18: 2129. https://doi.org/10.3390/rs11182129
APA StyleChapman, J. W., Thompson, D. R., Helmlinger, M. C., Bue, B. D., Green, R. O., Eastwood, M. L., Geier, S., Olson-Duvall, W., & Lundeen, S. R. (2019). Spectral and Radiometric Calibration of the Next Generation Airborne Visible Infrared Spectrometer (AVIRIS-NG). Remote Sensing, 11(18), 2129. https://doi.org/10.3390/rs11182129