UoNGBR: A Regional Assimilation Barotropic Tidal Model for the Great Barrier Reef and Coral Sea Based on Satellite, Coastal and Marine Data

Abstract

All available satellite altimetry, coastal and marine data have been used to develop a new assimilative barotropic tidal model over the Great Barrier Reef (GBR) and Coral Sea using the Oregon State University Tidal Inverse Software (OTIS) with the specific consideration of bathymetry and drag coefficients. The model, named the University of Newcastle Great Barrier Reef (UoNGBR), has a 2′ × 2′ spatial resolution and includes 37 major and shallow water tidal constituents. The key to the development of UoNGBR is the use of a high-resolution bathymetry model gbr100 (3.6″ × 3.6″, corresponding to 100 meters resolution) and a recent baroclinic GBR1 hydrodynamic model. The gbr100 provides more detailed and accurate bottom topography, while the GBR1 hydrodynamic model provides spatially variable drag coefficients. These are particularly important in our study area due to the existence of numerous islands, coral reefs and complex bottom topography. The UoNGBR and seven existing tidal models have been used to detide independent datasets from the coastal tide gauges and Sentinel-3A altimeter mission. The detided datasets are then compared to the UoNGBR-detided data. The results show that UoNGBR has the minimum root sum square value (25.1 cm) when compared to those (between 26.1 and 66.7 cm) from seven other models, indicating that UoNGBR is among the best models in predicting tidal heights in the GBR and Coral Sea. Over coastline and coastal zones, the UoNGBR’s mean RMS errors are ~18 and 5 cm, respectively, smaller than TPXO models, as well as about 1–5 cm smaller than FES2012 and FES2014. These suggest that the UoNGBR model is a major improvement over other models in coastline and coastal zones.

1. Introduction

The Great Barrier Reef and Coral Sea include 10 percent of the world’s reef ecosystems with more than 3000 coral reefs and 600 continental islands [1]. Due to bioenvironmental concerns about this marine conservation zone, an accurate knowledge of the hydrodynamics is a priority [2,3]. Tides cause tidal currents and variations in sea levels, which are considered as the major contributor to ocean hydrodynamics in the GBR [4]. Considerable fluctuations in bottom topography due to numerous continental islands and the existence of coral reefs lead to the tidal regime of the area being complicated [5,6,7]. There were many studies that have attempted to analyse tides over this region in northern and central GBR, as well as in Broad Sound [8,9,10,11,12].

Purely empirical tidal models, in which sea level observations from satellite altimetry and coastal tide-gauges are used, are not efficient in capturing the tidal complexity of this area [13]. This is mainly due to the lower spatial resolution of sea level observations and neglect of complexity of the bottom topography [14,15]. In addition, pure hydrodynamic models, in which conservations of mass and momentum are used to develop shallow water equations, are not of acceptable performance over this zone [14]. This is because these models are highly reliant on the uncertainties of bathymetry and bottom friction [15,16]. Inaccurate initial inputs lead to the development of an inefficient tidal model, this implies that modelling by just applying the conceptual equations cannot represent all details of tidal phenomena [17].

The assimilation approach improves the tidal model outputs by constraining tidal shallow water equations using empirical observations, which is an effective method to develop accurate tidal models over coastal zones [18,19]. Models such as HAMTIDE [20], FES2014 [21], FES2012 [22] and TPXO9 [23] have confirmed the capability of assimilation approaches in improving outcomes of the hydrodynamic models.

Due to complex bathymetry, knowing the exact bottom topography is crucial to study the dynamics of the area including the mixing patterns, ocean tides, current flow and surface circulations [24]. Therefore, an accurate bathymetry model is the main precursor to develop a new tidal model for coastal zones [25]. In this regard we use a high-resolution bathymetry model (3.6″ × 3.6″), named gbr100, in developing a new tidal model for the GBR and Coral Sea in this study. The gbr100 covers the entire GBR and Coral Sea region [24].

In addition, previous studies have shown that in contrast to a sand type of sea floor, over coral reefs, such as the GBR, drag coefficients and bottom friction fluctuate noticeably [26]. As such, detailed information about the variations of bottom drag coefficients will contribute to better understanding of tidal behaviour in this area. Such information is now available from a recent hydrodynamic model by [27]. Furthermore, long-term datasets are available for this region from multi-satellite altimetry missions, coastal tide gauges, current meters (mooring) and shipborne Acoustic Doppler Current Profiler (SBADCP).

In this study, the Oregon State University Tidal Inversion Software (OTIS) by [28] is used to assimilate empirical observations into hydrodynamic equations in the GBR and Coral Sea. All available data and dynamics can be combined using the OTIS software tool to develop a new tidal model. This software uses a representer method [28] to assimilate available tidal data into shallow water equations. In this software a set of programs efficiently conduct representer calculation, generate efficient grids, prior model covariance, boundary conditions and implement tidal data inversion [29]. Compared to other assimilation algorithms, OTIS benefits from further simplifications, which facilitate tidal assimilation modelling over large scales but with limited computation expenses. In addition, further updates of this software provide users with capability of using sea surface current data from moorings and ship borne ADCPs [30].

The new tidal model for the GBR and Coral Sea developed in this study is named as the UoNGBR model. The resultant model has a spatial resolution of 2′ × 2′. It uses the most recent bathymetry model for the study area and addresses what role the reef plays in tidal behaviour of the region by accounting for variations of the drag coefficient over reef and non-reef areas. It includes 37 tidal constituents of major and shallow water types: M₂, S₂, K₁, P₁, N₂, O₁, Q₁, S₁, K₂, 2N₂, eps₂, J₁, L₂, La₂, R₂, T₂, M₃, M₄, M₆, M₈, MKS₂, MK₃, MN₄, MS₄, Mu₂, Nu₂, S₄, N₄, OO₁, SO₁, Mf, Mm, Sa, Ssa, Msf, Msqm and Mtm.

The remainder of the paper is structured as follows. The study area and datasets are described in Section 2. A description of implementing the model is presented in Section 3. In Section 4 sensitivity analysis of the contribution of bathymetry and drag coefficient data to the new model in the study area is discussed. The results, validations, conclusions and further discussions are presented in Section 5 and Section 6.

2. Study Area and Data

The study area is located in the GBR and Coral Sea, geographically extending from latitudes 10°S to 26°S and longitudes 142°E to 156°E and covering the continental shelf and slope of Queensland’s coastline, Australia. The GBR is located at the western margin of the Coral Sea with numerous reefs ranging in area from 0.01 to 100 km², which has created a complex bottom topography and thus complex hydrodynamics [5,31].The average depth over the GBR is 35 m but plunging into more than 5000 m in the Coral Sea. Therefore, in this paper we define four different zones, namely coastline, coastal, shelf and (deep) ocean zones, according to bathymetry. The performance of the new tidal model UoNGBR will be evaluated over these zones (Figure 1).

The datasets used in the implementation and evaluation of UoNGBR are classified as model input and validation data. Both data types include satellite altimetry, coastal and marine observations that are further described in Section 2.1 and Section 2.2.

2.1. Input Data

The data from multi-satellite altimetry missions of Topex/Poseidon (T/P), Jason-1, Jason-2, Envisat and ERS-2 are used in the UoNGBR tidal modelling. Other input datasets include sea level and current measurements from coastal tide gauges, moorings and shipborne ADCP.

2.1.1. Multi-Satellite Altimetry Missions

During 1992–2002, the T/P altimeter provided unprecedented accurate observations of sea levels. Continuing on T/P’s observations and orbital arguments, the sea level was measured by Jason-1 from 2002 to 2009, and then followed by OSTM Jason-2 from 2009 to 2016. The current Jason-2 mission is still on the orbit and records sea level observations. Therefore, the sea level observation time series for this set of altimeter missions in this study is formed from 1992 to 2016, a total 25 years. The along-track distance between two successive footprints of a pass over the sea is about 7 km, while the distance between two passes is about 315 km at the equator. In addition, 3-year data from Jason-1’s interleaved orbit is also used in this study. These missions were specifically designed to study ocean dynamics, including circulations and tides [32]. Sea level observations from these missions are suitable to study ocean tides owing to their short repeat period of 9.9156 days and highly accurate orbital accuracy of few centimetres [33].

The ERS-2 and Envisat missions have a longer repeat period of 35 days, compared to that of the T/P series, and a smaller distance between two successive orbits at the equator. ERS-2 observed the sea level from 1995 to 2003, while Envisat extended the survey on the same orbit as ERS-2 from 2003 to 2010, producing altogether a valuable time-series of sea level observations. However, the sun-synchronous orbit of these missions fails to see sun-caused constituents such as S₁, S₂ and S₄ [34]. The multi-mission altimetry data used in this study are available from the Radar Altimeter Database System (RADS, rads.tudelft.nl). The satellite data implemented in this study has been summarized in

Table 1. The satellite data used in this study.

Mission	Years	Repeat Period (Days)	Cross Track Distance in GBR (km)	Type *
T/P + Jason-1 + Jason-2	1992–2016	9.9156	300	I
Jason-1 Phase B	2009–2012	9.9156	300	I
ERS-2 + Envisat	1995–2010	35	76	I
Sentinel-3A	2016–2019	27	99	V

* “I” stands for input and “V” for validation data.

.

2.1.2. Coastal Tide Gauges

Sea-level observations recorded at 19 tide gauges between 1991 and 2015 (

Table 2. The geographic position and period of observation records for coastal tide gauges.

Station No.	Tide Gauge Dame	Latitude (Degrees)	Longitude (Degrees)	Time Duration		Type *
				Start Date	End Date
1	Bowen Storm	−20.01	148.25	01/01/1996	31/12/2015	I
2	Bundaberg	−24.76	152.38	01/01/1996	31/12/2015	I
3	Cairns Storm	−16.93	145.78	01/01/1996	31/12/2010	I
4	Cape Ferguson	−19.26	147.05	01/01/1996	31/12/2015	I
5	Cardwell	−18.25	146.03	01/09/1991	31/12/2015	I
6	Clump Point	−17.83	146.1	01/01/1997	31/12/2015	I
7	Cook Town	−15.45	145.25	01/01/1996	31/12/2015	I
8	Fishermans Landing	−23.78	151.16	01/01/2002	31/12/2015	I
9	Gladstone	−23.83	151.25	01/01/1996	31/12/2015	I
10	Mackay	−21.1	149.21	01/01/1996	31/12/2006	V
11	Mourilyan	−17.6	146.11	01/01/1996	31/12/2015	I
12	Port Alma	−23.58	150.86	01/01/1996	31/12/2015	I
13	Rosslyn Bay	−23.16	150.8	01/01/2001	31/12/2015	I
14	Shute Harbour	−20.28	148.78	01/01/1996	31/12/2015	I
15	South Trees	−23.85	151.3	01/01/1996	31/12/2015	V
16	Thursday Island	−10.56	142.21	01/01/1996	31/12/2015	I
17	Townsville	−19.25	146.83	01/01/1996	31/12/2011	V
18	Urangan	−25.3	152.91	01/01/1996	31/12/2015	I
19	Alotau	−10.31	150.45	01/01/1996	31/12/2015	I

* “I” stands for input and “V” for validation data.

) were used in this study. The data have a high accuracy of 1 cm in all weather conditions [35] and a sample rate of one or half an hour. The tide gauge datasets are available from the Australian Bureau of Meteorology (BoM, http://www.bom.gov.au/oceanography/projects/abslmp/data/), Maritime Safety Queensland (http://www.msq.qld.gov.au/Tides/Open-data) and Permanent Service for Mean Sea Level (http://www.psmsl.org). The geographic distribution of tide gauges and altimetry tracks are depicted in Figure 2. The altimeter tracks are shown for T/P (in green), ERS-2/Envisat (in blue) and Sentinel-3A (in red). Tide gauge positions are shown in solid triangles.

2.1.3. Bathymetry

In order to address the importance of an accurate bathymetry model, two depth models of gbr100 [24] and General Bathymetric Chart of the Oceans (GEBCO) [36] are used in this study. The gbr100 bathymetry model uses the latest datasets obtained from ship-based multi-beam, single-beam and echo-sounder surveys, airborne LiDAR bathymetry surveys, and satellite remotely sensed data that is updated and delivered regularly. This model has a pixel size of 0.001-arc degree (or 3 arc seconds and is approximately 100 m) [24]. This model is available from the Deep Reef Explorer (https://www.deepreef.org/). The GEBCO model is the most publicly available depth model that provides bathymetry maps with different spatial resolutions at global and regional scales. This model benefits from new sounding data that has improved over shallow water regions. The GEBCO_2014 version of this bathymetry model with a spatial resolution of 30″ × 30″ is used in this investigation (http://www.gebco.net/data_and_products/gridded_bathymetry_data/). The accuracy of the bathymetry models has been determined as an approximate 0.5% of the depth value [37]. Thus, the deeper the grid node is located, the larger its depth error is expected to be. This source of error is due mainly to the sounding systematic and environmental associated errors [38], which escalate in deeper zones. The Mean Sea Level (MSL) is used as the height datum for depth values in both the gbr100 and GEBCO_2014 models [24,36].

2.1.4. Mooring Network

The National Mooring Network in Integrated Marine Observing System (IMOS, http://imos.org.au/) provides physical and biological measurements of Australian coastal waters for scientific research projects. More than nine permanent stations installed on the seabed bottom measure the meridional (V) and zonal (U) current velocities over the study area. These in-situ measurements are made on a 30 min temporal resolution.

Table 3. The geographic position and period of observation records for mooring stations.

Mooring No.	Mooring Station Code	Latitude (Degrees)	Longitude (Degrees)	Time Duration
				Start Date	End Date
1	GBRCCH	−22.4083	151.9945	27/04/2009	02/10/2017
2	GBRHIN	−23.3836	151.9870	16/10/2009	07/10/2012
3	GBRHIS	−23.5123	151.9553	12/09/2007	05/10/2017
4	GBRLSH	−14.1718	145.6412	03/06/2009	19/05/2014
5	GBRLSL	−14.3393	145.3434	23/04/2011	20/05/2012
6	GBRMYR	−18.2184	147.3448	06/06/2009	15/11/2017
7	GBROTE	−23.4830	152.1728	17//08/2011	31/03/2017
8	GBRPPS	−18.3103	147.1634	25/10/2012	17/11/2017
9	NRSYON	−19.3051	147.6220	23/06/2008	26/09/2017

shows the station name, geographic position and period of observation records for each current meter supplied by the IMOS.

2.1.5. Shipborne ADCP

The OTIS software has the capability of processing ship borne ADCP data [30]. The acoustic Doppler shift profilers can be mounted on voyage ships and record the zonal (U) and meridional (V) components of sea currents in different ocean depth layers and for numerous geographical positions along the ship sailing track. Figure 3 shows the locations of mooring stations and sail tracks of different voyages along which U and V components have been recorded. The ship-borne ADCP data are from the Commonwealth Scientific and Industrial Research Organisation’s (CSIRO) Marlin Metadata System (http://www.marlin.csiro.au).

2.1.6. Drag Coefficient Values

In assimilated tidal models, at either a global or regional scale, the drag coefficient is usually considered to be a constant value as the seabed is predominately sand over the majority of seas and oceans. However, studies in the eastern Irish Sea [39], northern Gulf of Mexico [40] and the North Sea [41] have revealed that the value of drag coefficients vary from 0.0025 to 0.0029 under different conditions. In the GBR region, it has been reported that different seabed types can pose spatially varying drag coefficient values [26]. This coefficient varies noticeably from 0.0025 to 0.0048 over the GBR and Coral Sea. When compared to the constant value (0.003) for sand beds, this is of a considerable difference. This fact leads to considering the drag coefficient as a variable parameter in our modelling procedure. The spatially varying drag coefficient value based on the GBR1 Hydrodynamics Model [27] is adopted in this study, which can be obtained from the GBR1 hydrodynamic model database (https://research.csiro.au/ereefs/).

2.2. Validation Data

In order to evaluate the efficiency of the UoNGBR model, recent satellite Sentinel-3A altimeter datasets (2016–2019) were used (Table 1). Data from Sentinel-3A can be considered as an independent dataset, as they have not been used by existing tidal models at the time of this study. This altimetry satellite is part of Sentinel missions designed to provide measurements for monitoring the global environment [42]. Sentinel-3A has a sun-synchronous orbit and repeats every 27 days. It has been designed to observe the sea surface with an approximate accuracy of 2–3 cm [43]. Over the coastline zone, the UoNGBR model was validated against three coastal tide-gauge stations that have not been used in the model development (Table 2). The distribution of Sentinel-3A tracks and validation tide gauges can be seen in Figure 2. In addition, the UoNGBR model was validated against seven existing tidal models. For this, the sea level anomalies that include tides (SLAt) were detided using seven existing tidal models: FES2012, FES2014, TPXO8, TPXO9, GOT 4.10, DTU10 and EOT11a. The detailed description of these models can be found in [15,44].

3. Modelling Procedure

The modelling procedure in this study comprises of two main phases. In the first phase an empirical model is developed based on analysing data from coastal tide gauges and multi-satellite altimetry missions. Then, this model is used at the second phase as the source of open boundary conditions for the initial solution in OTIS software.

3.1. Empirical Tidal Model

In order to develop the empirical tidal model, the Remove–Compute–Restore method is used. This is the most adopted and applied approach in geosciences, especially in geodesy. It has been widely used in modelling the regional geoid using satellite gravity data and developing semi-empirical tidal models in recent years [45,46,47,48,49]. In this approach a base model (FES2014) is used to remove tides from SLAt data to calculate the Sea Level Anomaly (SLA). The SLAs are then analysed to extract tidal corrections. Finally, the tidal corrections are added back to constituents interpolated from the base model.

In order to extract tidal constants for major and shallow water tidal constituents, both the harmonic analysis and response method are used. Tide-gauge data are analysed using the harmonic analysis, while for altimetry observations a combination of both harmonic and response approaches are used. The detailed description of the empirical model has been presented in [50]. The resultant 37 tidal constants of long-term, major and shallow water constituents are adopted as open boundary conditions in the forward solution of OTIS software.

3.2. Use of OTIS Software

The assimilation approach used in OTIS is a generalized inverse method (GIM), which is based on minimizing an explicitly defined penalty function [51]. It uses the GIM to assimilate data into the shallow water tidal equations. An explicitly defined penalty function, which includes both data and dynamics, is minimized using a least squares method [51]. The major difficulty in solving the GIM is the large size of the coefficient matrixes. For tackling this problem in OTIS an efficient representer method has been applied [52]. The large size of matrices can be reduced by eliminating velocities from shallow water equations, which decreases the number of unknowns [53]. However, instead of eliminating velocities, OTIS solves the linearized hydrodynamic equations using an iterative process that minimizes the penalty function [54]. For this purpose, an initial solution for the unknowns (i.e., tidal constituent constants) are calculated by solving linearized shallow water equations. Then, the initial solution is used through an iterative process to gain a solution that best fits both empirical observations and tidal hydrodynamic equations. The mathematical formulation of OTIS is briefly shown as follows [51,52,55]:

The empirical observations constitute equations as

$$d=Lu$$

(1)

where d is the observation vector and L the measurement functions which relate the observed data to the unknown tidal state u. On the other hand, the tidal hydrodynamic equations are

$$Su=f_0$$

(2)

where u is the tidal state, including tidal zonal and meridional current components (U, V) and tidal height (ξ), S the matrix of hydrodynamic equations and f₀ the astronomical forcing. Therefore, in the assimilation, the set of equations to be solved are of the form as

$$\begin{array}{l}\left[\begin{array}{l}S\\ L\end{array}\right]u=\left[\begin{array}{l}{f}_0\\ d\end{array}\right]\end{array}$$

(3)

In order to estimate the true tidal state (u), Equation (3) must be solved. Although it is theoretically possible to find a solution of u₀ which satisfies Equation (2), in general no tidal state (u) will satisfy Equation (3). This means that the operator, formed by a combination of data functional (L) and hydrodynamic (S) equations, is singular. The GIM, as used in OTIS, essentially constructs a generalized inverse of this operator [28]. Meanwhile, as there is no exact tidal state (u) to satisfy Equation (3), the inverse calculation is proposed as a fitting problem through an iterative process with both data and hydrodynamic constrains. However, the feasibility of this assimilation method has been of concern due to the size of matrices in computations. For tackling this problem in the representer approach, every element of data functional vector (L_k) is represented by element r_k in the unknown parameters space (u), which is the reason that this method is known as representer approach. In the fitting iterative process, the final tidal state ($\stackrel{⌢}{u}$) is computed as

$$\stackrel{⌢}{u}=u_0+{\displaystyle \sum _{k=1}^K{b}_k{r}_k}$$

(4)

where b is the matrix of coefficients. Therefore, the inverse tidal problem in OTIS is based on the calculation of the representers (r) for the data functionals (L), and then solving Equation (4) in order to find the unknown vector ($\stackrel{⌢}{u}$). The location of these representers, according to the default of OTIS, is the altimetry crossover points where the empirical observations have a higher density.

In order to estimate 37 tidal constants using OTIS software in this study, the empirical model developed by [50] is used as the initial tidal model and consequently the source of open boundary conditions. The output of this stage will be an initial solution that is used in the assimilation procedure. Based on the features of OTIS, we design the modelling procedure of the UoNGBR model (Figure 4), which assimilates input data in GBR and Coral Sea into shallow water equations using OTIS software [56].

In the GBR, the mooring networks record the zonal (U) and meridional (V) velocities on a temporal resolution of 30 min (Table 3). These current meters mounted on the sea bottom are able to measure the sea current velocities at different depths (Figure 3). Therefore, we used the harmonic analysis to extract the amplitude and phase of U and V for tidal constituents that are to be assimilated using OTIS. In addition, the U and V from ADCP profiles shown in Figure 3 were also used in assimilation, as the OTIS software has the capability of processing shipborne ADCP data [30]. Furthermore, the tidal constants of 37 tidal constituents extracted from coastal tide-gauges (harmonic analysis) and satellite altimetry data (harmonic and response analysis) [50] are assimilated into hydrodynamic equations.

Before implementing OTIS software, in order to investigate the possible contribution of the new bathymetry model, gbr100, and spatially variable drag coefficient values to tidal modelling over the GBR, a sensitivity analysis was performed. The final output of OTIS implementation is the UoNGBR model with 37 tidal constituents.

4. Sensitivity Analysis

The hydrodynamics of shallow water regions, estuaries, straits and bays is affected by uncertainties in both bottom friction and bathymetric data [57,58,59,60,61]. Bathymetric data has been known as an important input to shallow water hydrodynamic modelling [62,63], while the influence of the drag coefficient value on tides in coastal regions has been reported by other studies [64,65].

Over coastal areas, the non-linearity of shallow water tidal equations is more important due to their contribution to complexity of the tidal spectrum in these regions [19,66]. This complex non-linearity results in shallow water tidal components being produced, which provide comparable amplitudes to some major constituents in coastal regions. The generation of these short wavelength waves is due to the interaction between major constituents with themselves or other components, which overall is caused by bottom topography and friction. In this section, a numerical assessment is implemented based on a sensitivity analysis to investigate the role of two main inputs of tidal hydrodynamic equations: Bathymetry and drag coefficients. For validation, Sentinel-3A and coastal tide gage data are used.

The sensitivity analysis was conducted using OTIS. In order to assess the improvement of bathymetry, both gbr100 and GEBCO models are considered. To evaluate the contribution of drag coefficient values, a constant value of 0.003, the default value in OTIS, and spatially variable drag coefficient values are considered. The test area subjected to this assessment is geographically bounded by longitudes 147°E to 153°E and latitudes 23°S to 19°S in the GBR.

4.1. Bathymetry Effects

This set of tests concerns the effect of different bathymetry models of gbr100 and GEBCO (cf. Section 2.1.3). First, the linearized shallow water equations are solved using the forward solution in OTIS software. This is done using depth from gbr100 and then GEBCO model, respectively, while keeping all other conditions unchanged in both implementations. Second, the estimated tidal constituents are used to predict the tidal height, which is consequently used to detide SLAts observed by Sentinel-3A and coastal tide gauges. Finally, the Root Mean Square (RMS) of the SLAs based on different bathymetry models (

Table 4. Mean root mean square (RMS) of sea level anomalies (SLAs) based on bathymetry models gbr100 and GEBCO in the test area (cm).

Zone	Mean RMS Based on gbr100	Mean RMS Based on GEBCO
CL	37.8	53.7
CZ	17.8	31.5
SZ	11.5	17.0
OZ	6.6	6.7

) are estimated and compared over coastline (CL), coastal (CZ), shelf (SZ) and deep ocean (OZ) zones (cf. Figure 1).

The results shown in Table 4 support that using a more accurate bathymetry model will generate a more efficient tidal model. The most significant contribution of gbr100 appears over coastline and coastal zones, where the difference between mean RMS errors of SLAs based on gbr100 and GEBCO is 15.9 cm and 13.7 cm, respectively. Over the shelf zone, the mean RMS error based on gbr100 is ~6 cm smaller than that based on GEBCO, while the difference of mean RMS errors can be neglected over the deep ocean zone. In order to further assess the difference between two models in estimating tidal constituents over four zones, eight semi-diurnal, diurnal and shallow water constituents (e.g., M₂, S₂, K₁, P₁, M₄, M₆, MK₃ and S₄) are considered. For a given constituent j, the RMS error of model difference is calculated as [67]

$$RM{S}_j={\left(\frac{1}{2N}{\displaystyle \sum _{i=1}^N{\left(H_i^{gbr100}-H_i^{GEBCO}\right)}^2}\right)}^{1/2}$$

(5)

where N is the number of locations in a zone, and H the complex form of tidal amplitude and phase. Figure 5 shows the mean RMS errors of eight constitutes with the bathymetry gbr100 and GEBCO models. It can be seen that semi-diurnal constituents are mainly affected by the choice of bathymetry data when compared to shallow water constituents over this region. The M₂ has a mean RMS of ~38 cm, ~25 cm and ~8.5 cm in coastline, coastal and shelf zones, respectively. The S₂ has a mean RMS of ~15 cm, ~7.5 cm and ~3 cm in these three zones, respectively. Although the impact of bathymetry data on shallow water constituents is not considerable, M₆ is more affected with the mean RMS error of ~0.4 cm and ~0.35 cm over the coastline and coastal zone, respectively. It was found that all types of constituents are insensitive to the selection of bathymetry data over the deep ocean zone.

It is acknowledged that the ocean bottom topography affects the coastal processes including tides. The tidal response of the oceans, wavelength of tidal waves proceeding to the coastline and interaction between major tidal constituents, that produces tidal shallow water components, are influenced by fluctuations of bathymetry [68,69,70]. Therefore, the high-resolution bathymetry model gbr100 significantly contributes to much more precise estimations of tidal constants than the GEBCO model.

4.2. Drag Coefficient Effects

The drag coefficient varies depending on the type of the sea bottom texture, which changes throughout the whole area of interest [26]. Most assimilative tidal models take this parameter as a constant value and assume that the sea bottom is mostly covered by sand. However, over the GBR and Coral Sea this parameter has been found to vary from 0.0025 to 0.0048 according to the GBR1 Hydrodynamics Model [27]. Therefore, in this section, the forward solution of OTIS software is used to assess the role of drag coefficient values in tidal modelling over the test area.

First, the linearized shallow water equations are solved with the OTIS default drag coefficient value (0.003). Second, a spatially varying drag coefficient value, which is one of the by-products of GBR1 hydrodynamic model, is used. Finally, the two models generated from the constant and varying drag coefficients are used to predict tidal heights and accordingly detide the sea level observations of coastal tide-gauges and SLAts from Sentinel-3A over the test area.

Table 5. The role of drag coefficient values—mean RMS errors of SLA differences (cm).

Zone	Mean RMS Based on Spatially Varying Drag Coefficients	Mean RMS Based on the Constant Drag Coefficient
CL	37.8	40.1
CZ	17.8	19.6
SZ	11.5	12.7
OZ	6.6	6.6

shows the numerical results of this statistical comparison. The mean RMS of calculated SLAs are estimated and discussed.

According to Table 5, over the coastline and coastal zones, the use of a spatially variable drag coefficient can better address the presence of the reefs over the study area. When comparing the results using varying drag coefficients to those using the constant coefficient, the mean RMS errors drop 2.1 cm, 1.8 cm, and 1.2 cm over CL, CZ and SZ zones, respectively. The results over the deep ocean zone show that models have the same quality no matter which types of drag coefficients are used. We also computed the mean RMS errors of the eight constituents with the constant and varying drag coefficients based on Equation 5 over four different zones (Figure 6).

From Figure 6, the drag coefficient mainly affects the semi-diurnal constituents, and less affects diurnal and shallow water constituents. The M₂ has the maximum RMS errors of ~3.5 cm, ~3 cm and ~2.8 cm over coastline, coastal and shelf zones, respectively. The S₂ has the second maximum RMS error around 1.0 cm over all zones, except for the deep ocean. Using the spatially variable drag coefficient or constant value does not significantly influence the diurnal constituents (RMS < 0.4 cm), and the shallow water constituents (RMS < 2 mm) in particular.

The drag coefficient is an important factor in determining the bottom friction in tidal hydrodynamics [71]. Tidal waves are interacting with seabed bottom on their way proceeding to coastal and shelf zones. Considering a realistic value for drag coefficients in a coastal region contributes to precise estimation of tidal constituents [72]. Therefore, accounting for variations of drag coefficients over coastline, coastal and shelf zones, induced by the type of the sea bottom, is another factor that contributes to the new assimilative tidal model over this area. Our sensitivity analysis results (Table 5 and Figure 6) suggest that using the spatially variable drag coefficient will better address the presence of reefs in an assimilative tidal model than using the constant value.

5. Results

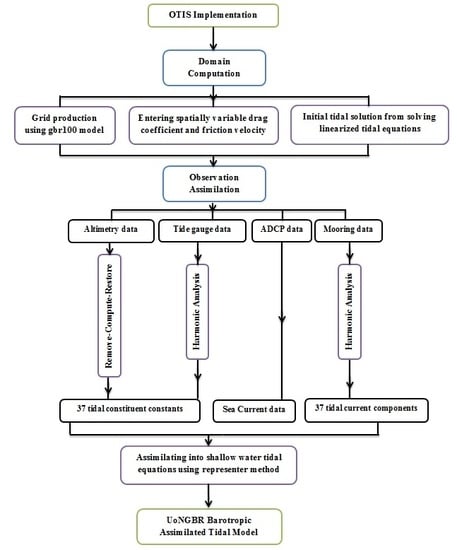
From results shown in the sensitivity analysis in Section 4, it can be seen that over the GBR and Coral Sea, in particular over coastal and shelf zones, the high-resolution bathymetry and non-constant drag coefficient have to be considered. Followed the flowchart (Figure 4) and using the OTIS software, our assimilative tidal model UoNGBR was, thus, generated by the datasets from more than 25 years of satellite altimetry, coastal tide gauges, mooring and ship-born ADCP data, bathymetry model gbr100 and spatially varying drag coefficient values based on the GBR1 Hydrodynamics Model [27]. In order to evaluate the efficiency of the UoNGBR model, coastal tide gauges and Sentinel-3A SLAts were used (cf. Figure 2). The results and performance of the UoNGBR model over the study area are discussed in this section.

The performance of the UoNGBR model is assessed in four different zones (cf. Figure 1). For model validation, the UoNGBR-derived ocean tide corrections are used to detide the SLAts made by both tide gauges and Sentinel-3A. In addition, the SLAts are detided using other seven tidal models, including FES2012, FES2014, TPXO8, TPXO9, GOT 4.10, DTU10 and EOT11a. The RMS of the detided SLAs is then computed for each tidal model. The magnitude of RMS of the SLAs can be used to assess the efficiency of the tidal models, with the small RMS indicating the better performance of the model. The comparison among computed mean RMS errors are shown in

Table 6. The mean RMS (cm) of the SLAs and Root Sum Square (RSS) (cm) in the study area with the bold value indicating the minimum mean RMS (or RSS).

Model	Coastline	Coastal Zone	Shelf Zone	Deep Ocean Zone	RSS
UoNGBR	18.8	11.6	8.8	8.1	25.1
FES2012	19.7	12.3	8.8	8.0	26.1
FES2014	23.1	16.4	8.9	8.1	30.8
TPXO8	35.1	16.0	10.4	8.2	40.8
TPXO9	38.1	17.4	11.2	8.3	44.2
GOT 4.10	24.6	14.7	10.3	8.1	31.5
DTU10	33.2	15.3	7.7	10.6	38.9
EOT11a	56.3	29.5	17.9	10.4	66.7

and Figure 7. In order to assess the overall performance of models, the Root Sum Square (RSS) of mean RMS values over all four zones were calculated from:

$$RSS={\left({\displaystyle \sum _{i=1}^{4}RM{S}_i^2}\right)}^{1/2}$$

(6)

In Table 6, both TPXO8 and TPXO9 have been implemented by the representer approach proposed in OTIS, which is the same approach as used for UoNGBR. It can be seen that UoNGBR performs more efficiently than TPXO9 and TPXO8 with the mean RMS differences (TPXO-UoNGBR) of 19.3 cm and 16.3 cm, respectively, over the coastline. In addition, mean RMS differences between TPXO models and UoNGBR over coastal and shelf zones are ~5 cm and ~3 cm, respectively. These noticeable mean RMS differences suggest that tidal estimations have been significantly improved in UoNGBR due to several reasons, such as using a more accurate bathymetry, spatial variable drag coefficients, editing the OTIS default for representer locations and including more tidal constituents. The major improvement lies in shallow water regions, where an accurate knowledge of bathymetry is crucial. According to Andersen (1999), the spatial advection of tidal energy from deep to shallow zones is proportional to the square of the water level. This fact reflects on the contribution of the accurate bathymetry used in UoNGBR (i.e., gbr100). Over the deep ocean zone, the three models of UoNGBR, TPXO9 and TPXO8 show similar performance.

The numerical results shown in Table 6 indicate that spatially varying drag coefficients make important contributions to efficiency of the assimilative tidal model UoNGBR. A seabed of reef type has large drag coefficient values compared to the sand seafloor [26]. In global tidal models, such as TPXO8 and TPXO9, the drag coefficient may be represented as a constant value, as the majority of sea and ocean beds is of sand type. However, for regional tidal models over GBR, due to the presence of reefs, neglecting the variations of drag coefficients can reduce the accuracy of the model. The UoNGBR is modelled using spatially varying drag coefficients with a more realistic representation of the seabed type, exposing the model to an accurate bottom friction and consequently more accurate tidal constituent amplitudes and phases.

While every altimetry along-track profile and tide gauge locations can be considered as representers, it is impractical to run OTIS due to the size of the matrices. Egbert et al. (1994) proposed that a subset of data locations can be used as representers to tackle matrix size issues. It has been found that the most efficient data locations to be used as representers are where higher density of observations exist [56]. Therefore, altimetry crossover points are ideal data locations to be considered as representer positions. However, through the modelling experiments it was found that the crossovers located close to the coastlines should be excluded. This is due to the errors associated with altimetry sea-level observations over shallow waters [73]. Thus, these altimeter crossovers were excluded from the list of representer locations, and were replaced by the closest tide gauge. This resulted in more accurate tidal height predictions from the UoNGBR model.

In the GBR area, empirical models (e.g., DTU10, GOT4.10 and EOT11a) fail to provide accurate tidal heights in comparison to UoNGBR (Table 6), as expected. Although both DTU10 and GOT 4.10 show more efficient results than EOT11a, they are far less accurate than UoNGBR, especially over coastline, coastal and shelf zones. FES2012 outperforms its successor, FES2014, with the mean RMS difference of ~3 cm over the coastline and coastal zones, while over the shelf and deep ocean zones they both are similar (RMS errors 8.8 cm vs. 8.9 cm). UoNGBR outperforms FES2012 (RMS errors 18.8 cm vs. 19.7 cm) and FES2014 (RMS errors 18.8 cm vs. 23.1 cm) over the coastline. In the coastal zone, this model is still more favourable with the mean RMS being ~1 cm and ~5 cm smaller than FES2012 and FES2014, respectively. The new UoNGBR model performs at the same accuracy level as FES2012 and FES2014 over the shelf and deep ocean zones.

To assess the model capability of predicting tidal heights, Figure 7 shows the geographical distribution of calculated pointwise RMS values of SLAs over the study area. From Figure 7, it seems that all models act similarly in deep oceans, while in the shelf zone EOT11a is not as accurate as other models in terms of the tidal height prediction. The models of EOT11a, FES2014, TPXO9, GOT4.10 and DTU10 appear to have inefficiencies, with RMS errors > ~30 cm, in tidal high prediction over all or parts of this area. FES2012 shows an overall acceptable performance and is known as the best model for this region [44]. However, it is observed that FES2012 is slightly less accurate than UoNGBR at ~1 cm of mean RMS over coastline and coastal zone from Table 6. The area with large uncertainties along the coastline can be clearly seen in Figure 7.

The coastline and coastal zone are the main regions that model discrepancies are observed. Over these areas, UoNGBR shows a higher performance, followed by FES2012, GOT4.10 and DTU10. According to Figure 7, the area bounded by latitudes 20°S to 23°S and longitudes 146° to 151° is where large accuracy discrepancies are shown among models. Our previous study has found that there are sudden fluctuations in bottom topography due to existence of small islands [60], which is the main reason behind the model inefficiencies. Therefore, we defined this area as the challenging area [44].

Table 7. The mean RMS of the SLAs in the challenging area over different zones (cm) with bold value indicating the minimum mean RMS.

Model	Coastline	Coastal Zone	Shelf Zone	Deep Ocean Zone	RSS
UoNGBR	26.8	11.5	9.1	8.7	31.9
FES2012	31.1	13.1	9.1	8.6	36.0
FES2014	44.6	24.4	9.6	8.6	52.4
TPXO8	32.8	22.8	10.7	8.7	42.2
TPXO9	35.9	22.9	13.7	8.8	45.2
GOT 4.10	29.2	18.6	11.3	8.5	37.4
DTU10	28.6	21.1	11.8	8.7	33.7
EOT11a	58.1	39.1	22.3	10.5	74.2

shows the performance of models in different zones of the challenging area.

Table 7 reveals the prime performance of UoNGBR over other models in the challenging area. The RSS differences between UoNGBR and FES2012, FES2014 and TPXO8 are ~4, ~21 and ~10 cm, respectively. The considerable difference in the challenging area between UoNGBR and other models mainly lays in coastal zones. Coastal zones in the challenging area include Broad Sound and the Southern GBR, where it is well known to have a complex tidal regime due to complicated bathymetry. Since this area is featured with high fluctuation of bathymetry, the superior efficiency of UoNGBR can be assigned to the use of the high-resolution bathymetry model gbr100. A closer look at the amplitude and phase of M₂, interpolated from the UoNGBR model, reveals why tidal models face difficulties in modelling the tidal wave over coastal zones especially in the challenging zone (Figure 8).

From Figure 8, it can be seen that over most of the GBR and Coral Sea the amplitude of M2 (top left) shows a monotonic behaviour. Over coastal zones, where most of coral reefs are located, this constituent’s amplitude is magnified, in particular in the challenging area, where amplitudes exceed more than 150 cm near the coastline. The intense variations can also be seen in the phase map (top right in Figure 8) over the continental slope, where the depth reduces from more than 2000 m to 100 m. This sudden variation in depth affects the phase and amplitude of long wavelength M₂ waves, which are further magnified when proceeding to the coastline. This confirms the fact that accurate knowledge of the bottom geometry of this area is crucial, for which this study has addressed the issue by using the more accurate bathymetry model gbr100.

The U and V tidal current maps of M₂ (bottom panels in Figure 8) show the fact how existence of small islands and coral reefs along the Queensland coastline shapes the pattern of tidal currents. While the tidal current speed is within a few cm/s over most of the study area, it exceeds 60 cm/s in the challenging zone. The tidal currents may contribute to (or threaten) growth and maintenance of the reef and its ecosystem health through exchanging nutrients and pollutants, as well as sediment and sand transport [9,74,75,76,77]. According to Figure 8, tidal currents in inner reefs are of high amplitudes, which play an important role in exchanging these materials on a daily basis.

6. Conclusions and Recommendations

In this study, the UoNGBR barotropic assimilated tidal model was developed using OTIS software for the GBR and Coral Sea. All available satellite altimetry and coastal sea level observations and marine sea current data for the region are used to constraint the shallow water tidal equations. This model includes 37 major and shallow water tidal constituents that have been spread on a regular grid of 2’ × 2’. The influences of using the new bathymetry model, gbr100, and spatially variable drag coefficient were investigated in a sensitivity analysis and the results are shown in Figure 5 and Figure 6 and Table 3 and Table 4. The sensitivity analysis shows that using the high-resolution bathymetry model, gbr100, and spatially variable drag coefficients largely contribute to the estimation of major tidal constituents in this area. Since the new bathymetry has a high spatial resolution of 3.6″ × 3.6″, it is able to provide accurate information about sudden fluctuations in bathymetry due to the small islands and coral reefs. Figure 5 and Figure 6 reveal that new datasets improve the accuracy of major tidal constituents more than shallow water components. Our new tidal model benefited from detailed information about dynamics of the area, resulting in relatively superior performance to other models especially over areas with highly complex bottom topography. The UoNGBR data can be found in supplementary files associated with this paper.

There are challenges over the GBR region, which can be the main error sources for the UoNGBR model and thus subject to future studies. Some parts of the GBR region are too shallow at low tides and become deeper at high tides. This proposes the high rate of variations in bottom friction. Although the drag coefficient variations have been spatially considered in this study, their temporal variation features have not yet been investigated. In addition, the simplifications made in OTIS, such as using linearized shallow water equations, can be a source of error for the new model. Furthermore, a cross validation of how input datasets with different temporal and spatial scales affect the robustness of assimilated models should be considered in future studies.

The bathymetry in this study has been considered as constant in value. However, in reality due to the existence of numerous islands and coral reefs, bathymetry varies noticeably [6]. The constant bathymetry may not represent the reality of seafloor topography. In addition, while the 2′ × 2′ grid resolution was generated for the UoNGBR model, it is possible to use a multiple resolution grid for this area due to existence of the higher spatial resolution bathymetry [24]. In other words, a denser grid can be used over highly varying bathymetry areas, while the sparse grids can be taken over deeper ocean zones. Therefore, for future research, it is suggested that using higher order terms of bottom friction, time variant bathymetry and multi-resolution grids can further contribute to better understanding of tides in the GBR and Coral Sea.