Model Simulation and Prediction of Decadal Mountain Permafrost Distribution Based on Remote Sensing Data in the Qilian Mountains from the 1990s to the 2040s

Abstract

Based on the results of remote sensing data interpretation, this paper aims to simulate and predict the mountain permafrost distribution changes affected by the mean decadal air temperature (MDAT), from the 1990s to the 2040s, in the Qilian Mountains. A bench-mark map is visually interpreted to acquire a mountain permafrost distribution from the 1990s, based on remote sensing images. Through comparison and estimation, a logistical regression model (LRM) is constructed using the bench-mark map, topographic and land coverage factors and MDAT data from the 1990s. MDAT data from the 2010s to the 2040s are predicted according to survey data from meteorological stations. Using the LRM, MDAT data and the factors, the probabilities (p) of decadal mountain permafrost distribution from the 1990s to the 2040s are simulated and predicted. According to the p value, the permafrost distribution statuses are classified as ‘permafrost probable’ (p > 0.7), ‘permafrost possible’ (0.7 ≥ p ≥ 0.3) and ‘permafrost improbable’ (p < 0.3). From the 1990s to the 2040s, the ‘permafrost probable’ type mainly degrades to that of ‘permafrost possible’, with the total area degenerating from 73.5 × 10³ km² to 66.5 × 10³ km². The ‘permafrost possible’ type mainly degrades to that of ‘permafrost impossible’, with a degradation area of 6.5 × 10³ km², which accounts for 21.3% of the total area. Meanwhile, the accuracy of the simulation results can reach about 90%, which was determined by the validation of the simulation results for the 1990s, 2000s and 2010s based on remote sensing data interpretation results. This research provides a way of understanding the mountain permafrost distribution changes affected by the rising air temperature rising over a long time, and can be used in studies of other mountains with similar topographic and climatic conditions.

1. Introduction

Permafrost is defined as the ground (including soil, rock, etc.) which remains at or below 0 °C for at least two consecutive years [1,2]. Mountain permafrost is simply the occurrence of permafrost in high mountain areas, which usually distributes in mid-latitude mountains with high elevations [3]. The Qilian Mountains is one of the most important regions for distributing mountain permafrost in the Qinghai-Tibet Plateau, even in China. Influenced by greenhouse gases, global warming is bound to result in the degradation of mountain permafrost in the Qilian Mountains [4,5]. The distribution area of mountain permafrost in the Qilian Mountains has a good potential for gas hydrate prospecting [6]. Moreover, the degradation of the mountain permafrost is a major driving factor of intensifying desertification [7], which also affects such things as biochemical processes and human infrastructure in the Qilian Mountains [8,9]. Meanwhile, mountain permafrost degradation has an important link to natural disasters, such as freezing-dissolving disasters [3]. Given these facts, it is essential to understand and simulate the mountain permafrost degradation status affected by the air temperature in the Qilian Mountains, which has both scientific and economic significance [10].

The distribution status of mountain permafrost cannot be wholly achieved by field survey, so computer modeling for the spatial distribution of mountain permafrost parameters becomes a useful tool and is widely researched [11], such as, based on topographic parameters [12], in the regional climate model (RCM) [13], bottom temperature of snow cover (BTS) [14,15,16], logistical regression model (LRM) [17,18,19,20], equivalent elevation [3], air temperature and ground temperature. These models simulate the permafrost distribution status under different conditions using various methods, but seldom predict the permafrost distribution and its change affected by climate change over a long time, which is also meaningful.

The objective of this paper is to simulate and predict the mountain permafrost distribution status in the past and future decades, from the 1990s to the 2040s, in the Qilian Mountains, based on remote sensing interpretation results. To achieve this goal, the mean decadal air temperature (MDAT) data for every decade from the 2010s to the 2040s are predicted according to the survey data from the 1960s to the 2000s at every meteorological station. Then, based on a bench-mark map of permafrost distribution, acquired from remote sensing images, the LRM is built according to topographic parameters, land coverage factors and MDAT data from the 1990s. Finally, based on the LRM and MDAT data from the 1990s to the 2040s, the mountain permafrost distribution in the Qilian Mountains is simulated and predicted for every decade using LRM; its accuracy can be validated from the 1990s to the 2010s using remote sensing interpretation results. The change tendency of mountain permafrost in the Qilian Mountains can be better understood by this research, which can also be extended to other mountains with similar terrains and climates.

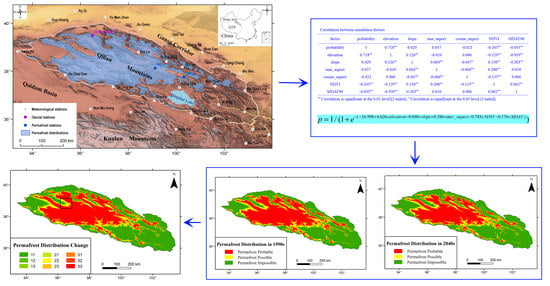
2. Study Area

Located in the western part of China and northeastern part of the QTP, the Qilian Mountains are situated between the Qaidam Basin and the Gansu Corridor (Figure 1). The relief shading map in Figure 1 shows that, with a northwest-southeast trend, the Qilian Mountains are composed of a series of parallel mountain chains and broad valleys.

In the Qilian Mountains, most of the peaks are higher than 4000 m asl (above sea level), and the high elevation induces mountain permafrost, which belongs to the Qilian-Altun Permafrost Sub Region of the QTP Permafrost Region. Controlled mainly by elevation and latitude, the low air temperature is the major climate factor affecting the distribution of mountain permafrost. With global warming, the increase of air temperature will inevitably result in the degradation of the mountain permafrost in the Qilian Mountains.

3. Methodology

3.1. Data Acquisition

The data source used in this research includes a bench-mark map of the mountain permafrost distribution in the Qilian Mountains, topographic parameters, land coverage factors and MDAT data.

3.1.1. Bench-Mark Map

Based on aerial and satellite images, the bench-mark map was made by referencing survey data and relevant literature, such as the Frozen Ground Map along the QTP Road (1:600,000), Geomorphology Map in the Qilian Mountains (1:1M), Natural Landscape Map in the QTP (1:3M), the Quaternary Glacial Relics Map in the QTP (1:3M), Snow, Ice and the Frozen Map of China (1:4M), etc. Finally, it was completed at 1:3M in 1996 [21].

By revising and processing the benchmark map, the mountain permafrost distribution status in the Qilian Mountains is shown in Figure 1, which mainly represents the permafrost distribution results of the 1990s.

3.1.2. Topographic Parameters

Topographic parameters include elevation, slope, and the sine and cosine values of the aspect.

Elevation reflects the roughness and height degree of the ground surface [22], which is the main factor affecting the distribution of mountain permafrost, because elevation has an important effect on the distribution of natural environment conditions, such as climate and vegetation [23]. In this research, the elevation data are acquired by processing Shuttle Radar Topographic Mission data with 3-arc seconds spatial resolution. In spatial processing, the elevation data have a spatial resolution of 0.001° and geographic projection, which are the same for other factors. In the final elevation data, the highest, lowest and average elevations in the Qilian Mountains are 5763 m asl, 1576 m asl and 3586 m asl respectively.

Slope reflects the oblique degree of the ground surface, which can determine the scale and intensity of the flow and energy transformation of ground materials [24,25]. Slope factor is acquired based on elevation data through spatial calculation. In the Qilian Mountains, the value range and mean value of the slope data are 0–69.3° and 12.1°, respectively.

Aspect can result in a difference in solar radiation energy, so it can affect the lower limit of the mountain permafrost distribution. Aspect is an important factor for many mountain permafrost simulation models [12,22,26]. Based on elevation data, aspect is computed through spatial calculation. The values of the aspect are circular data ranging from 0–360°, so it is difficult to directly use them in the simulation model. To solve this problem, the sine and cosine values of the aspect are computed.

3.1.3. Land Coverage Factor

The land coverage factor is used to present the distribution status of the ground surface. In this research, it is represented by the Normalized Difference Vegetation Index (NDVI), which is used to monitor the coverage degree and growth status of ground vegetation through band computation of remote sensing images [27]. The value range of NDVI is from −1 to 1. Negative values indicate that the ground coverage is cloud, water or snow, etc.; 0 represents rock or exposed soil; and positive values indicate that the ground is covered by vegetation; these values increase with the increase of the vegetation coverage.

The NDVI data are acquired by processing the 1km AVHRR Global Land Dataset, and the acquisition time is August, 1995. Through spatial processing, the final NDVI data have the same resolution and projection as other factors. In the final NDVI data, the value range is from −0.99 to 0.80, which represents the different land coverage statuses.

3.1.4. MDAT Data

MDAT data are acquired based on the survey data of 27 meteorological stations in and around the Qilian Mountains, which are shown in Figure 1. From the survey data, the MDAT data for every decade from the 1960s to the 2000s, at every meteorological station, can be computed.

For every meteorological station, a curve estimation regression is carried out on the MDAT data for every decade, from the 1960s to the 2000s, using different regression models, including linear, quadratic, compound, growth, logarithmic, cubic, S, exponential, inverse, power and logistical. By estimating the Sig. and R² of every regression model, the best regression model can be determined. Generally, the selected model has a Sig. below 0.05 and an R² greater than 0.8 for every meteorological station. Thus, the predicted value can be credible, and the MDAT data in every decade from the 2010s to the 2040s can be predicted for every meteorological station.

Based on the MDAT data for every decade from the 1990s to the 2040s at the meteorological stations, the linear regression model is built using the MDAT data, topographic factors (including elevation, slope, sine value and cosine value of the aspect), and location parameters (latitude and longitude) at the F probability of 0.05, which is shown in

Table 1. Linear regression model using MDAT and other factors for every decade from the 1990s to the 2040s.

Decade	Linear Regression Model	R2
1990s	MDAT90=111.624 − 5.647 × [elevation]/1000 − 1.3016 × [latitude] − 0.4460 × [longitude]	0.948
2000s	MDAT00=114.902 − 5.716 × [elevation]/1000 − 1.3180 × [latitude] − 0.4669 × [longitude]	0.949
2010s	MDAT10=114.930 − 5.612 × [elevation]/1000 − 1.3109 × [latitude] − 0.4702 × [longitude]	0.937
2020s	MDAT20=115.390 − 5.572 × [elevation]/1000 − 1.3053 × [latitude] − 0.4744 × [longitude]	0.928
2030s	MDAT30=115.867 − 5.529 × [elevation]/1000 − 1.3003 × [latitude] − 0.4785 × [longitude]	0.917
2040s	MDAT40= 116.305 − 5.481 × [elevation]/1000 − 1.2952 × [latitude] − 0.4822 × [longitude]	0.903

.

The following can be found in Table 1: MDAT data have a close relation to elevation, latitude and longitude, and the R² is above 0.90, so it is acceptable to simulate MDAT data for the whole of the Qilian Mountains using these linear regression models for the decades from the 1990s to the 2040s.

The longitude and latitude factors are built first. The final raster data of latitude and longitude have the same resolution and projection as other factors, and the value of every pixel in the data is the latitude or longitude of the pixel.

Then, the MDAT data for the whole of the Qilian Mountains can be simulated using the linear regression models in Table 1. By subtracting the simulation data from the survey data at every meteorological station, the residual MDAT data are acquired. Using the proper interpolation method, the residual MDAT data for the whole of the Qilian Mountains can be computed. By adding the interpolated residual MDAT data to the simulation data, the final MDAT data for the whole of the Qilian Mountains have the same values with as original data from the meteorological stations. The final MDAT data in the 1990s and the 2040s are shown in Figure 2.

The final MDAT have similar distribution in the 1990s and 2040s, so the data in other decades are omitted in Figure 2. In the final MDAT data, the values at the meteorological stations are equal to the survey data from the same meteorological stations. To quantitatively analyze the MDAT data, a statistical analysis is conducted, as shown in

Table 2. Statistical analysis of the MDAT data for the Qilian Mountains (°C).

	Decades	1990s	2000s	2010s	2020s	2030s	2040s
Statistics
Maximum		9.15	9.66	9.64	9.85	10.07	10.40
Minimum		−14.80	−14.62	−14.07	−13.61	−13.13	−12.63
Mean		−2.04	−1.69	−1.34	−0.95	−0.54	−0.12
Standard Deviation		3.82	3.83	3.76	3.71	3.66	3.61

.

The MDAT data are low in the eastern part, basins and lakes, such as the Qinghai Lake, which is high in the upper part of the mountains with high elevations, as shown in Figure 3 and Table 2. From the 1990s to the 2040s, the MDAT data continually increased, and the mean value increased by nearly 2.0 °C.

3.2. Model Construction

The aim of the model construction is to build the relationship between the mountain permafrost distribution and other factors, such as topographic factors, NDVI data and MDAT data. Through comparison and estimation, LRM is chosen in this research.

Compared to the linear regression model, LRM does not require the dependent variable to have the character of normal distribution. Additionally, the LRM is proper when the dependent variable is the binomial classified variable. Permafrost distribution has two statuses of existence and inexistence, which is fit for LRM. Hence, the LRM has been introduced to simulate mountain permafrost distribution in recent years [17,18,19,20] The LRM can estimate the probability of a certain condition occurring (‘permafrost existence’ or ‘permafrost inexistence’ in this research) by calculating the changes in the log odds of the dependent variable, the equation of which is the following:

$$\ln [p/(1-p)]=A+Bx+Cy\dots$$

(1)

where p/(1 − p) is log odds of the probability of the mountain permafrost existence or inexistence; A is the regression constant; B and C are coefficients; and x and y are predictors. In order to compute p directly, Equation (1) can also be expressed as follows:

$$p=1/(1+e^{-(A+Bx+Cy\dots )})$$

(2)

Completed in 1996, the benchmark map provides the distribution status of mountain permafrost in the Qilian Mountains in the 1990s. The probability is 1 when mountain permafrost exists, and 0 in the inverse condition. The MDAT data for the 1990s are selected for the model construction.

The values of the mountain permafrost distribution probability, topographic factors, NDVI, and MDAT data in the 1990s are assigned to the sample points, which are evenly distributed in the Qilian Mountains at an interval of 0.1°. The number of sample points is 1991. Based on the values of the 1991 sample points, the correlations between the simulation factors are computed in

Table 3. Correlations between simulation factors.

Factor	Probability	Elevation	Slope	Sine_Aspect	Cosine_Aspect	NDVI	MDAT90
Probability	1	0.718 **	0.029	0.037	−0.021	−0.103 **	−0.693 **
Elevation	0.718 **	1	0.126 **	−0.019	0.006	−0.129 **	−0.939 **
Slope	0.029	0.126 **	1	0.064 *	−0.047	0.150 **	−0.203 **
Sine_Aspect	0.037	−0.019	0.064 *	1	−0.060 *	0.200 **	0.010
Cosine_Aspect	−0.021	0.006	−0.047	−0.060 *	1	−0.135 **	0.006
NDVI	−0.103 **	−0.129 **	0.150 **	0.200 **	−0.135 **	1	0.062 *
MDAT90	−0.693 **	−0.939 **	−0.203 **	0.010	0.006	0.062 *	1

**: Correlation is significant at the 0.1 level (2-tailed); *: Correlation is significant at the 0.05 level (2-tailed).

.

The following can be found in Table 3: distribution probability has a close correlation with elevation, MDAT and NDVI; as for the slope, the sine and cosine value of aspect, the correlation is low; and the correlation between elevation and MDAT is relatively high, which is due to the close relation between temperature and elevation.

As the correlations between distribution probability and other factors varies largely, LRM is constructed using the ‘forward stepwise (conditional) method,’ with a stepwise probability of 0.05 according to the values at the 1991 sample points:

$$p=1/(1+e^{-(-16.998+4.626\times elevation-0.040\times slope+0.386\times \sin e\_aspect-0.745\times NDVI-0.176\times MDAT)})$$

(3)

According to the stepwise probability of 0.05, the cosine value of the aspect is excluded in the LRM. The Cox & Snell and Nagelkerke R² are 0.542 and 0.725 respectively. Taking the cut value of the probability as 0.5, the number of corrected classified sample points is 1746, which accounts for 87.7% of the total sample points. Hence, it is feasible to use LRM to simulate the mountain permafrost distribution in the Qilian Mountains, which provides a basis for predicting the mountain permafrost distribution in the future.

3.3. Model Validation Introduction

To validate the model simulation results, the achievements from remote sensing data interpretation can be taken as the referencing results; meanwhile, some areas are randomly selected to strengthen the accuracy of the validation process.

3.3.1. Referencing Results

Based on remote sensing data interpretation, the referencing results can be acquired from the 1990s to the 2010s.

In this research, three referencing results are obtained to validate the model simulation results, which are acquired during the 1990s, the 2000s and the 2010s respectively, to correspond to the model simulation results from the 1990s, the 2000s and the 2010s respectively.

The referencing results can be visually interpreted from remote sensing images and other relevant literature, or computed from the indexes based on different bands combination, or acquired from other remote sensing retrieved climate factors that are close to permafrost distribution.

The referencing results are acquired at a fixed time, whereas the simulation results represent mountain permafrost distribution in a decade. Meanwhile, the model simulation results should be divided into different types according to probability. The time difference and type division of the model simulation results may bring a deviation at some point in the model validation process.

3.3.2. Random Areas Selection

Random area selection is conducted using the boundary of the Qilian Mountains and the ArcToolbox of the ArcGIS software.

Firstly, 100 random points are created with a minimum distance of 10,000 m; then, a buffer analysis is conducted for every random point with a radius of 5000 m; finally, the buffer areas are taken as the random areas in this research. Due to the distance restriction in the random point creation process, the random areas do not have overlapping conditions. The distribution of the random areas is shown in Figure 3.

Figure 3 shows that the distribution of the random areas is sparse and has no rules, which presents another way for model simulation validation process.

4. Results

4.1. Validation of the Model Simulation Results in Different Periods

The model simulation results were validated in the 1990s, 2000s and 2010s, based on remote sensing interpretation results.

4.1.1. Validation of the Model Simulation Results from the 1990s

Downloaded from the USGS, the global Landsat remote sensing images were acquired with composite bands of 7, 4 and 2 and acquisition phases of around 1990 and around 2000. Based on the remote sensing images and other relevant data, the Geomorphologic Atlas of the People’s Republic of China was visually interpreted at a scale of 1:250,000 [28], which can be downloaded from the website of the Environmental and Ecological Science Data Center for West China.

In the Geomorphologic Atlas, geomorphology is divided into many genesis types in China, such as glacial, periglacial, lacustrine, fluvial, loess and arid types [28]. Periglacial geomorphology distributes in the boundary which is lower than that of the glacial geomorphology and higher than that of the fluvial geomorphology. The Qilian Mountains are located in the middle latitude regions where periglacial geomorphology has similar distribution than that of the mountain permafrost [24].

As the boundary between the periglacial geomorphology and permafrost region is approximate [24], the simulation result can be validated by referencing the periglacial geomorphologic distribution in the Geomorphologic Atlas, which is shown in Figure 4a.

The result of a comparison of the simulation results from the 1990s and the periglacial geomorphology distribution of the Geomorphologic Atlas is shown in Figure 5a:

The following can be found in Figure 5a: two widely-distributed types are 01 and 13, which are non-permafrost and permafrost regions, respectively, in both the simulation and referencing results; the 02 and 12 types are also widely distributed, but much less so; and the 03 and 11 types are misclassified types, which have a limited distribution.

The results of the area statistics of every type in Figure 5a are shown in

Table 4. Area statistics of the model validation results from the 1990s to the 2010s (×10³ km²).

	Type	01	02	03	11	12	13
Period
1990s		81.3	17.4	11.7	8.8	13.3	61.8
2000s		77.1	11.8	4.1	14.2	19.0	68.2
2010s		73.2	18.6	3.1	2.5	12.1	67.9

.

The following can be found in Table 4: for the simulated result from the 1990s, the area of the completely corrected types (01 and 13) is 143.1 × 10³ km², which accounts for 73.6% of the total area; the area of the basically corrected types (02 and 12) is 30.7 × 10³ km², which accounts for 15.8% of the total area; and the area of the misclassified types (03 and 11) is 20.5 × 10³ km², which accounts for 10.6% of the total area.

For the randomly selected areas in Figure 3, the area statistics of the model validation results are computed from the 1990s to the 2010s, which are shown in

Table 5. Area statistics of the model validation results in the randomly selected areas from the 1990s to the 2010s (km²).

	Type	01	02	03	11	12	13
Period
1990s		3485.5	666.9	542.5	348.9	426.7	2172.4
2000s		3007.7	392.8	166.4	881.2	699.5	2495.4
2010s		3137.6	684.6	147.8	110.8	406.9	2456.4

.

Table 5 presents the model validation results in the randomly selected areas from the 1990s, and the following can be found in Table 5: the area of both completely corrected types is 5657.9 km², which accounts for about 74.0% of the total area; the area of both basically corrected types is 1093.6 km², which accounts for 14.3% of the total area; and the area of both misclassified types is 891.4 km², which accounts for 11.7% of the total area. The validation results in the whole Qilian Mountains and in the randomly selected areas show that the accuracy of the simulated result is about 90% in the 1990s, which includes the completely corrected types and basically corrected types.

4.1.2. Validation of the Model Simulation Result from the 2000s

Passive microwave remote sensing has the advantage of being able to monitor the freeze/thaw state of the surface soil over long periods on different scales. Based on Special Sensor Microwave/Imager brightness temperature data, frozen and thawed soil can be distinguished using a decision tree algorithm. The classification accuracy of the decision tree algorithm was evaluated using the map of geocryological regionalization and classification in China. Through a grid-to-grid Kappa analysis, the overall classification accuracy was 91.7%, and that of the Kappa index was 80.5% [29].

Using the frozen and thawed soil classification based on passive microwave remote sensing retrieval result and the decision tree algorithm and the map of the geocryological regionalization and classification in China [30], the referencing result from the 2000s can be acquired, as shown in Figure 4b.

The results of the comparison of the simulation result and referencing result are shown in Figure 5b. The following can be found in Figure 5b: other than the two main types, 01 and 13, the 12 type also has a wide distribution; the next widest distributions are found in the 11 and 02 types; and the 03 type is too little to see.

The results of the area statistics of every type in Figure 5b are computed and are shown in Table 4. From Table 4, the following can be found: the area of the completely corrected types (01 and 13) accounts for 74.7% of the total area; the area of the basically corrected types (02 and 12) accounts for 15.8% of the total area; and the area of the misclassified types (03 and 11) accounts for 9.5% of the total area.

Table 5 computed the validation of the model simulation result in the randomly selected areas from the 2000s. From Table 5, we can find the following results: the area of the both completely corrected types accounts for 72.0% of the total area; the area of the basically corrected types accounts for 14.3% of the total area; and the area of the both misclassified types accounts for 13.7% of the total area. From the validation in the whole Qilian Mountains and the randomly selected areas we can see that, including both the completely and basically corrected types, the accuracy of the simulated result is about 90% in the 2000s.

4.1.3. Validation of the Model Simulation Result from the 2010s

Based on the borehole point data, annual mean ground temperature data in the Qinghai-Tibet Plateau was simulated using the land surface temperature product and infrared radiometer survey data of the moderate resolution imaging spectroradiometer. On the basis of the annual mean ground temperature data, ground surface observation temperature data from an automatic weather station and DEM data, a Permafrost Distribution Map in the Qinghai-Tibet Plateau from 2009 to 2013 was acquired using ground surface freezing number model [31].

The reference data from the 2010s were acquired from clipping the Permafrost Distribution Map in the Qinghai-Tibet Plateau from 2009 to 2013 using the boundary of the study area. The permafrost distribution map of the reference data is shown in Figure 4c.

The boundary of the map in Figure 4c does not completely cover that of the study area, so the area’s statistical results for the validation from the 2010s are a little lower than those from the 1990s and the 2000s. The result of the comparison of the reference data and the simulation data is shown in Figure 5c.

From Figure 5c and the enlarged picture, we find the following: 01 and 13 are the main types, followed by the 02 type; the 12 type has s sparse distribution, and the 03 and 11 types are difficult to find.

The results of the area statistics of every type in Figure 5c are shown in Table 4. From this table, it can be seen that the area of both the 01 and 13 types is 141.1 × 10³ km², which accounts for 79.5% of the total area; the area of both the 02 and 12 types is 30.7 × 10³ km² and accounts for 17.3% of the total area; and the area of both the 03 and 13 types is 5.6 × 10³ km² and accounts for 3.2% of the total area.

The validation result from the 2010s in the randomly selected areas is computed in Table 5, in which can be found the following: the area of the both completely corrected types is 5594.0 km² and accounts for 80.6% of the total area; the area of the both basically corrected types is 1091.6 km² and accounts for 15.7% of the total area; and the area of the both misclassified types is 258.6 km² and accounts for 3.7% of the total area.

From the area statistical results, by including both the completely and basically corrected types, the accuracy of the simulation result in 2010s is above 95%. Overall, by validating the simulation results from the 1990s, 2000s and 2010s, the accuracy of the simulation results can reach 90%.

4.2. Model Simulation and Prediction Results of Mountain Permafrost Distribution from the 1990s to the 2040s

Assuming the factors, except for the MDAT unchangeable factor, the distribution probability of mountain permafrost for every decade from the 1990s to the 2040s is simulated and predicted based on the LRM. The maximum and minimum values of the distribution probability are 1 and 0 respectively. The results of a statistical analysis of the mean and standard deviation values are shown in

Table 6. Statistical analysis of the distribution probability of mountain permafrost in the Qilian Mountains.

	Decades	1990s	2000s	2010s	2020s	2030s	2040s
Statistics
Mean		0.456	0.450	0.444	0.438	0.430	0.423
Standard Deviation		0.393	0.393	0.391	0.390	0.389	0.387

:

The distribution probability decreases steadily from the 1990s to the 2040s, which indicates persistent degradation of the mountain permafrost distribution during the same period, as shown in Table 6. According to the value of the distribution probability, the mountain permafrost distribution is divided into 3 classes: p > 0.7 refers to the area of the ‘permafrost probable’ type; 0.3 ≤ p ≤ 0.7, the ‘permafrost possible’ type; p < 0.3, the ‘permafrost impossible’ type. Based on the division criteria, the distribution status of mountain permafrost in the whole Qilian Mountains and local area for the 1990s and the 2040s is shown in Figure 6.

Mountain permafrost has a similar distribution for the 1990s and 2040s, so their distributions for other decades are omitted in Figure 6. The following can be found in Figure 6: the ‘permafrost probable’ type is mainly distributed in the upper part of the Qilian Mountains, with a high elevation; the ‘permafrost impossible’ type, in the lower part with a lower elevation; and the ‘permafrost possible’ type is mainly distributed in the middle part, between the regions of the ‘permafrost probable’ type and those of the ‘permafrost impossible’ type, such as valleys, basins, etc. Besides mainly distributed regions, sparsely distributed ‘permafrost probable’ and ‘permafrost possible’ areas also exist. Generally, the distribution of the three classes does not vary significantly from the 1990s to the 2040s.

The results of the computation of the area of every class concerning mountain permafrost distribution, shown in Figure 6, are presented in

Table 7. Area of every class of mountain permafrost distribution in the Qilian Mountains (×10³ km²).

	Decades	1990s	2000s	2010s	2020s	2030s	2040s	Change	%
Statistics
Permafrost impossible		90.1	91.3	92.4	93.7	95.1	96.5	6.4	7.1
Permafrost possible		30.7	30.8	30.9	31.0	31.2	31.3	0.6	2.0
Permafrost probable		73.5	72.3	71.0	69.6	68.1	66.5	−7.0	−9.6

.

In Table 7, the ‘Change’ column provides the changes from the 1990s to the 2040s, and the ‘%’ column presents the percentage change compared to the distribution area in the 1990s. The ‘permafrost probable’ area decreases by 7.0 × 10³ km² from the 1990s to the 2040s, which accounts for 9.6% of the total area of ‘permafrost probable’. Moreover, the decreasing rate becomes higher and higher from the 1990s to the 2040s. The ‘permafrost possible’ and ‘permafrost impossible’ areas increase by 0.610³ km² and 6.4 × 10³ km², respectively, from the 1990s to the 2040s. The increase of the two classes is due to the degradation of the ‘permafrost probable’ area. The change of the three classes has the same tendency from the 1990s to the 2040s.

4.3. Distribution Change of Mountain Permafrost in the Qilian Mountains from the 1990s to the 2040s

The distribution change of mountain permafrost is limited in two adjacent decades, while it is apparent during the whole period from the 1990s to the 2040s. Hence, the distribution change of mountain permafrost in the Qilian Mountains from the 1990s to the 2040s is computed and shown in Figure 7.

The results of area statistics of every type of distribution change from the 1990s to the 2040s during two adjacent decades and the whole period are shown in

Table 8. Area statistics of every type of distribution change of mountain permafrost from the 1990s to the 2040s during two adjacent decades and the whole period in the Qilian Mountains (×10³ km²).

	Type	11	12	13	21	22	23	31	32	33
Period
From the 1990s to the 2000s		89.9	0.2	0.0	1.4	29.1	0.2	0.0	1.4	72.0
From the 2000s to the 2010s		91.1	0.2	0.0	1.3	29.2	0.3	0.0	1.5	70.8
From the 2010s to the 2020s		92.1	0.3	0.0	1.5	29.1	0.3	0.0	1.7	69.3
From the 2020s to the 2030s		93.4	0.3	0.0	1.6	29.1	0.3	0.0	1.8	67.8
From the 2030s to the 2040s		94.8	0.3	0.0	1.7	29.2	0.3	0.0	1.9	66.2
From the 1990s to the 2040s		90.0	0.2	0.0	6.5	24.0	0.2	0.0	7.2	66.3

:

From Figure 7 and Table 8, we can see the following: the distributions of the ‘permafrost probable’, ‘permafrost possible’ and ‘permafrost impossible’ areas are mainly unchanged; the ‘permafrost probable’ type mainly degrades to that of ‘permafrost possible’; the ‘permafrost possible’ type mainly degrades to that of ‘permafrost impossible’; with the rising air temperature, the degrading rate increase; and other changes are very limited.

5. Discussion

5.1. Model Effectiveness

Compared to other simulation models concerning permafrost distribution, such as the models for mountain permafrost based on topographic parameters which lack climate factors [12,22], the models based on RCM alone which lack topographic parameters [13], the models based on BTS survey data which have a series of problems acquiring BTS measurements [32], the terrestrial ecosystem models in simulating high-latitude permafrost regions [33], the stochastic model in calculating the probability density function of active-layer thickness [34], and the LRM model used in previous research [17,20], the LRM used in this research has some unique characteristics.

The LRM simulates and predicts the mountain permafrost distribution status in the Qilian Mountains for every decade based on MDAT and other factors. It obtains the change tendency of mountain permafrost over 50 years at a decadal scale. As for the relevant researches, the permafrost distribution on the QTP was simulated and predicted in 1999, 2049 and 2099 using a response model and global circulation model [35,36,37]. Janke examined the potential past and future mountain permafrost distribution, assuming a 4 °C range of cooler and warmer temperatures [26], which only provides hypothetical scenarios, without corresponding times or periods. Hence, this study has great significance for the simulation and prediction results of mountain permafrost distribution in this research, which have high-quality and long, continuous decadal periods.

Based on the bench-mark distribution map of mountain permafrost, LRM in this research is built based on the value of the 1991 sample points, which are evenly distributed in the Qilian Mountains. Compared to other simulation models which were built from filed survey data, the model construction method in this research overcomes the dependence on field surveys. Moreover, it provides a useful mountain permafrost simulation technique for remote regions, where it is difficult to conduct a field survey [38].

The LRM used in this research chooses several kinds of factors, such as topography, NDVI and MDAT. Moreover, through the correlation computation of every two factors and the stepwise probability determination during LRM construction, the unnecessary factors, such as the cosine value of the aspect in this research, are omitted so as to build the most proper LRM in this research, which provides a factor selection mechanism for LRM construction.

5.2. Model Validation

Based on the achievements of remote sensing data interpretation, the model simulation results are validated in the whole Qilian Mountains and in the randomly selected areas from the 1990s to 2010s. There are some aspects that should be illustrated in the model validation process.

The accuracy of the simulation results in the whole Qilian Mountains is a little higher than that in the randomly selected areas. This is because of the random distribution of the selected areas. If the areas are selected again, the accuracy comparison results may be reversed. Meanwhile, the generally accuracy distribution in the randomly selected areas is similar to that in the whole Qilian Mountains. So we take the accuracy estimation results in the whole Qilian Mountains as the standard, and those of the randomly selected areas as the reference.

The area of glaciers in the Qilian Mountains is about 1.9 × 10³ km², whereas the area of the mountain permafrost distribution in the Qilian Mountains exceeds 80 × 10³ km² [28,29,30,31]. Thus, glacier distribution can be neglected in this research, despite its having been used in relevant research [37,39].

According to the simulation results, the permafrost distribution statuses are divided into three types [17,18]. As to the reference results from the remote sensing achievements, the permafrost distribution statuses have two types: existence or non-existence. This difference may result in some deviations in the model validation process.

5.3. Model Limitations

The limitations of the simulation model are as the follows:

LRM was constructed using the distribution probability and factors from the 1990s, which cannot be fit completely into the other decades. Hence, the deviations cannot be eliminated using the constructed LRM to simulate and predict the distribution status of mountain permafrost for other decades [39].

A close relation exists between the predicators in the LRM (Table 3) [40]. For example, MDAT is computed by using elevation, latitude and longitude. The high correlation between topographic factors, NDVI and MDAT may decrease the robustness of the LRM.

LRM is considered as a scenario-type model in this research, which does not consider the lag time between the rising air temperature and mountain permafrost degradation [41]. In fact, with rising air temperatures, the thermal inertia of mountain permafrost and large amount of the ground ice will allow the mountain permafrost to exist for a time due to lag effect [42]. Meanwhile, other feedback mechanisms such as the precipitation factor are neglected in this research [26].

6. Conclusions

Based on remote sensing data and achievements, a decadal mountain permafrost distribution from the 1990s to the 2040s in the Qilian Mountains is simulated and predicted using LRM, MDAT data, topographic and land coverage factors. The following conclusions can be drawn from this research.

The ‘permafrost probable’ area, for every decade from the 1990s to the 2040s is 73.5 × 10³ km², 72.3 × 10³ km², 71.0 × 10³ km², 69.6 × 10³ km², 68.1 × 10³ km² and 66.5 × 10³ km² respectively. The distribution of the ‘permafrost impossible’, ‘permafrost possible’ and ‘permafrost probable’ areas are mainly unchanged; the ‘permafrost probable’ type mainly degrades to that of ‘permafrost possible’, and the degraded area is 7.2 × 10³ km², which is about 9.77% of the total area; the ‘permafrost possible’ type mainly degrades to that of ‘permafrost impossible’; and the degraded area is 6.5 × 10³ km², which is about 21.30% of the total area. By validating the simulation results, based on remote sensing interpretation results, the accuracy of the simulation results can reach 90% for the 1990s, 2000s and 2010s.

Glacier distribution is omitted in this research; meanwhile, the land coverage status cannot be fully represented by NDVI factor. In the future, potentially related researches on vegetation, glacier and permafrost engineering issues should be conducted in the Qilian Mountains and other regions with similar conditions [43,44].