Radar Altimetry as a Proxy for Determining Terrestrial Water Storage Variability in Tropical Basins
Abstract
:1. Introduction
2. Materials and Methods
2.1. Gravity Recovery and Climate Experiment (GRACE) Terrestrial Water Storage (TWS)
2.2. Radar Altimetry Data
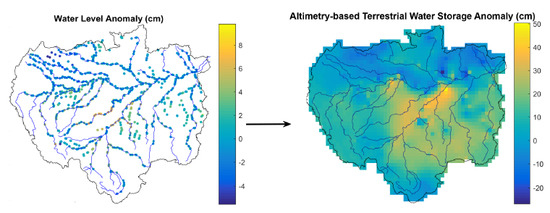
2.3. Estimating Terrestrial Water Storage from Radar Altimetry
2.4. Evaluation Procedure
3. Results
3.1. GRACE-Based TWS versus Radar Altimetry
3.2. Evaluation of the Regression-Based TWS Estimates
3.3. Interpolation Evaluation
3.4. Basin-Average TWS
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, n/a. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging trends in global freshwater availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef] [PubMed]
- Getirana, A. Extreme Water Deficit in Brazil Detected from Space. J. Hydrometeor. 2016, 17, 591–599. [Google Scholar] [CrossRef]
- Melo, D.D.D.; Wendland, E. Hydrological system time lag responses to meteorological shifts. Braz. J. Water Resour. 2016, 21, 766–776. [Google Scholar] [CrossRef] [Green Version]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A GRACE-based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [Green Version]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.J.; Syed, T.H.; Swenson, S.C.; de Linage, C.R.; Rodell, M. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Castellazzi, P.; Martel, R.; Rivera, A.; Huang, J.; Pavlic, G.; Calderhead, A.I.; Chaussard, E.; Garfias, J.; Salas, J. Groundwater depletion in Central Mexico: Use of GRACE and InSAR to support water resources management. Water Resour. Res. 2016, 52, 5985–6003. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhong, M.; Feng, W.; Zhang, Z.; Shen, Y.; Wu, D. Groundwater Depletion in the West Liaohe River Basin, China and Its Implications Revealed by GRACE and In Situ Measurements. Remote Sens. 2018, 10, 493. [Google Scholar] [CrossRef]
- Kumar, S.V.; Zaitchik, B.F.; Peters-Lidard, C.D.; Rodell, M.; Reichle, R.; Li, B.; Lia, B.; Jasinskia, M.; Mocko, D.; Getirana, A.; et al. Assimilation of Gridded GRACE Terrestrial Water Storage Estimates in the North American Land Data Assimilation System. J. Hydrometeor. 2016, 17, 1951–1972. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Steele-Dunne, S.C.; Gunter, B.C.; Ditmar, P.G.; Weerts, A.H. Data assimilation of GRACE terrestrial water storage estimates into a regional hydrological model of the Rhine River basin. Hydrol. Earth Syst. Sci. 2015, 19, 2079–2100. [Google Scholar] [CrossRef] [Green Version]
- Getirana, A.; Kumar, S.; Girotto, M.; Rodell, M. Rivers and Floodplains as Key Components of Global Terrestrial Water Storage Variability. Geophys. Res. Lett. 2017, 44, 10,359–10,368. [Google Scholar] [CrossRef] [Green Version]
- Frappart, F.; Papa, F.; da Silva, J.S.; Ramillien, G.; Prigent, C.; Seyler, F.; Calmant, S. Surface freshwater storage and dynamics in the Amazon basin during the 2005 exceptional drought. Environ. Res. Lett. 2012, 7, 044010. [Google Scholar] [CrossRef]
- Papa, F.; Frappart, F.; Güntner, A.; Prigent, C.; Aires, F.; Getirana, A.C.; Maurer, R. Surface freshwater storage and variability in the Amazon basin from multi-satellite observations, 1993–2007. J. Geophys. Res. Atmos. 2013, 118, 11,951–11,965. [Google Scholar] [CrossRef]
- Tourian, M.J.; Reager, J.T.; Sneeuw, N. The Total Drainable Water Storage of the Amazon River Basin: A First Estimate Using GRACE. Water Resour. Res. 2018, 54, 3290–3312. [Google Scholar] [CrossRef]
- Xavier, L.; Becker, M.; Cazenave, A.; Longuevergne, L.; Llovel, W.; Filho, O.C.R. Interannual variability in water storage over 2003–2008 in the Amazon Basin from GRACE space gravimetry, in situ river level and precipitation data. Remote Sens. Environ. 2010, 114, 1629–1637. [Google Scholar] [CrossRef]
- Hirschi, M.; Viterbo, P.; Seneviratne, S.I. Basin-scale water-balance estimates of terrestrial water storage variations from ECMWF operational forecast analysis. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Nie, N.; Zhang, W.; Zhang, Z.; Guo, H.; Ishwaran, N. Reconstructed Terrestrial Water Storage Change (ΔTWS) from 1948 to 2012 over the Amazon Basin with the Latest GRACE and GLDAS Products. Water Resour. Manag. 2016, 30, 279–294. [Google Scholar] [CrossRef]
- Becker, M.; Meyssignac, B.; Xavier, L.; Cazenave, A.; Alkama, R.; Decharme, B. Past terrestrial water storage (1980–2008) in the Amazon Basin reconstructed from GRACE and in situ river gauging data. Hydrol. Earth Syst. Sci. 2011, 15, 533–546. [Google Scholar] [CrossRef]
- Zeng, N.; Yoon, J.H.; Marengo, J.A.; Subramaniam, A.; Nobre, C.A.; Mariotti, A.; Neelin, J.D. Causes and impacts of the 2005 Amazon drought. Environ. Res. Lett 2008, 3, 014002. [Google Scholar] [CrossRef]
- Humphrey, V.; Gudmundsson, L.; Seneviratne, S.I. A global reconstruction of climate-driven subdecadal water storage variability. Geophys. Res. Lett. 2017, 44, 2300–2309. [Google Scholar] [CrossRef]
- Girotto, M.; De Lannoy, G.J.; Reichle, R.H.; Rodell, M.; Draper, C.; Bhanja, S.N.; Mukherjee, A. Benefits and Pitfalls of GRACE Data Assimilation: a Case Study of Terrestrial Water Storage Depletion in India. Geophys. Res. Lett 2017, 44, 4107–4115. [Google Scholar] [CrossRef] [PubMed]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Sun, A.Y.; Schmied, H.M.; van Beek, L.P.; Wiese, D.N.; Wada, Y.; Long, D.; Reedy, R.C.; et al. Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data. PNAS 2018, 115, E1080–E1089. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Birkett, C.M. Contribution of the TOPEX NASA Radar Altimeter to the global monitoring of large rivers and wetlands. Water Resour. Res. 1998, 34, 1223–1239. [Google Scholar] [CrossRef]
- Cazenave, A.; Nerem, R.S. Present-day sea level change: Observations and causes. Rev. Geophys. 2004, 42. [Google Scholar] [CrossRef]
- Birkett, C.M.; Reynolds, C.; Beckley, B.; Doorn, B. Coastal Altimetry; Springer: Berlin, Germany, 2011. [Google Scholar]
- Roux, E.; Santos da Silva, J.; Cesar Vieira Getirana, A.; Bonnet, M.P.; Calmant, S.; Martinez, J.M.; Seyler, F. Producing time series of river water height by means of satellite radar altimetry—A comparative study. Hydrol. Sci. J. 2010, 55, 104–120. [Google Scholar] [CrossRef]
- Da Silva, J.S.; Calmant, S.; Seyler, F.; Filho, O.C.R.; Cochonneau, G.; Mansur, W.J. Water levels in the Amazon basin derived from the ERS 2 and ENVISAT radar altimetry missions. Remote Sens. Environ. 2010, 114, 2160–2181. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.-C.; Nino, F.; del Rio, R.A.; Cazenavea, A.; et al. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Lee, H.; Beighley, R.E.; Alsdorf, D.; Jung, H.C.; Shum, C.K.; Duan, J.; Guo, J.; Yamazaki, D.; Andreadis, K. Characterization of terrestrial water dynamics in the Congo Basin using GRACE and satellite radar altimetry. Remote Sens. Environ. 2011, 115, 3530–3538. [Google Scholar] [CrossRef] [Green Version]
- Tseng, K.; Shum, C.K.; Kim, J.; Wang, X.; Zhu, K.; Cheng, X. Integrating Landsat Imageries and Digital Elevation Models to Infer Water Level Change in Hoover Dam. IEEE J. Select. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 1696–1709. [Google Scholar] [CrossRef]
- Getirana, A.; Jung, H.C.; Tseng, K.-H. Deriving three dimensional reservoir bathymetry from multi-satellite datasets. Remote Sens. Environ. 2018, 217, 366–374. [Google Scholar] [CrossRef]
- Getirana, A.C.V.; Peters-Lidard, C. Estimating water discharge from large radar altimetry datasets. Hydrol. Earth Syst. Sci. 2013, 17, 923–933. [Google Scholar] [CrossRef] [Green Version]
- Tarpanelli, A.; Brocca, L.; Barbetta, S.; Lacava, T.; Faruolo, M.; Moramarco, T. Integration of MODIS and Radar Altimetry Data for River Discharge Estimation from Space. In Engineering Geology for Society and Territory-Volume 3; Springer: Cham, Switzerland, 2015; pp. 607–610. [Google Scholar]
- Getirana, A.C.V. Integrating spatial altimetry data into the automatic calibration of hydrological models. J. Hydrol. 2010, 387, 244–255. [Google Scholar] [CrossRef]
- Getirana, A.C.V.; Boone, A.; Yamazaki, D.; Mognard, N. Automatic parameterization of a flow routing scheme driven by radar altimetry data: Evaluation in the Amazon basin. Water Resour. Res. 2013, 49, 614–629. [Google Scholar] [CrossRef] [Green Version]
- Paiva, R.C.D.; Collischonn, W.; Bonnet, M.P.; De Goncalves, L.G.G.; Calmant, S.; Getirana, A.; Santos da Silva, J. Assimilating in situ and radar altimetry data into a large-scale hydrologic-hydrodynamic model for streamflow forecast in the Amazon. Hydrol. Earth Syst. Sci. 2013, 17, 2929–2946. [Google Scholar] [CrossRef] [Green Version]
- Yamazaki, D.; Lee, H.; Alsdorf, D.E.; Dutra, E.; Kim, H.; Kanae, S.; Oki, T. Analysis of the water level dynamics simulated by a global river model: A case study in the Amazon River. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef]
- Winter, T.C.; Harvey, J.W.; Franke, O.L.; Alley, W.M. Ground Water and Surface Water; A Single Resource; DIANE Publishing Inc.: Darby, PA, USA, 1998. [Google Scholar]
- Mueller, B.; Hirschi, M.; Seneviratne, S.I. New diagnostic estimates of variations in terrestrial water storage based on ERA-Interim data. Hydrol. Process. 2011, 25, 996–1008. [Google Scholar] [CrossRef]
- Sun, A.Y.; Scanlon, B.R.; Zhang, Z.; Walling, D.; Bhanja, S.N.; Mukherjee, A.; Zhong, Z. Combining Physically-Based Modeling and Deep Learning for Fusing GRACE Satellite Data: Can We Learn from Mismatch? Water Resour. Res. 2019, 55, 1179–1195. [Google Scholar] [CrossRef]
- Okeowo, M.A.; Lee, H.; Hossain, F.; Getirana, A. Automated Generation of Lakes and Reservoirs Water Elevation Changes From Satellite Radar Altimetry. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 3465–3481. [Google Scholar] [CrossRef]
- Schutz, B.; Tapley, B.; Born, G.H. Statistical Orbit Determination; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global evaluation of new GRACE mascon products for hydrologic applications. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Riegger, J.; Tourian, M.J.; Devaraju, B.; Sneeuw, N. Analysis of grace uncertainties by hydrological and hydro-meteorological observations. J. Geodyn. 2012, 59–60, 16–27. [Google Scholar] [CrossRef]
- Wahr, J.; Swenson, S.; Velicogna, I. Accuracy of GRACE mass estimates. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J.; Milly, P.C.D. Estimated accuracies of regional water storage variations inferred from the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Fritsch, F.; Carlson, R. Monotone Piecewise Cubic Interpolation. SIAM J. Numer. Anal. 1980, 17, 238–246. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. Kriging: A method of interpolation for geographical information systems. Int. J. Geograph. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Gundogdu, K.S.; Guney, I. Spatial analyses of groundwater levels using universal kriging. J. Earth Syst. Sci. 2007, 116, 49–55. [Google Scholar] [CrossRef] [Green Version]
- Kholghi, M.; Hosseini, S.M. Comparison of Groundwater Level Estimation Using Neuro-fuzzy and Ordinary Kriging. Environ. Model Assess 2008, 14, 729. [Google Scholar] [CrossRef]
- Ozturk, D.; Kilic, F.; Ozturk, D.; Kilic, F. Geostatistical Approach for Spatial Interpolation of Meteorological Data. Anais Acad. Brasileira Ciências 2016, 88, 2121–2136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Theodossiou, N.; Latinopoulos, P. Evaluation and optimisation of groundwater observation networks using the Kriging methodology. Environ. Model. Softw. 2006, 21, 991–1000. [Google Scholar] [CrossRef]
- Pebesma, E.J. Multivariable geostatistics in S: the gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Sibson, R. A Brief Description of Natural Neighbor Interpolation. In Interpolating Multivariate Data; John Wiley & Sons: New York, NY, USA, 1981; pp. 21–36. [Google Scholar]
- Kurtzman, D.; Navon, S.; Morin, E. Improving interpolation of daily precipitation for hydrologic modelling: spatial patterns of preferred interpolators. Hydro. Process. 2009, 23, 3281–3291. [Google Scholar] [CrossRef]
- Dirks, K.N.; Hay, J.E.; Stow, C.D.; Harris, D. High-resolution studies of rainfall on Norfolk Island: Part II: Interpolation of rainfall data. J. Hydrol. 1998, 208, 187–193. [Google Scholar] [CrossRef]
- Da Silva, A.S.A.; Stosic, B.; Menezes, R.S.C.; Singh, V.P. Comparison of Interpolation Methods for Spatial Distribution of Monthly Precipitation in the State of Pernambuco, Brazil. J. Hydrol. Eng. 2019, 24, 04018068. [Google Scholar] [CrossRef]
- Lengerer, A.; Kazda, M. Surface interpolation of environmental factors as tool for evaluation of the occurrence of high methane and nitrous oxide fluxes. J. Plant Nutr. Soil Sci. 2018, 181, 51–60. [Google Scholar] [CrossRef]
- Sun, Y.; Kang, S.; Li, F.; Zhang, L. Comparison of interpolation methods for depth to groundwater and its temporal and spatial variations in the Minqin oasis of northwest China. Environ. Model. Softw. 2009, 24, 1163–1170. [Google Scholar] [CrossRef]
- Zhang, Y.; Xian, C.; Chen, H.; Grieneisen, M.L.; Liu, J.; Zhang, M. Spatial interpolation of river channel topography using the shortest temporal distance. J. Hydrol. 2016, 542, 450–462. [Google Scholar] [CrossRef] [Green Version]
- Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Getirana, A.C.V.; Boone, A.; Yamazaki, D.; Decharme, B.; Papa, F.; Mognard, N. The Hydrological Modeling and Analysis Platform (HyMAP): Evaluation in the Amazon Basin. J. Hydrometeor. 2012, 13, 1641–1665. [Google Scholar] [CrossRef] [Green Version]
- Getirana, A.; Peters‐Lidard, C.; Rodell, M.; Bates, P.D. Trade-off between cost and accuracy in large-scale surface water dynamic modeling. Water Resour. Res. 2017, 53, 4942–4955. [Google Scholar] [CrossRef] [PubMed]
- Kosuth, P.; Callède, J.; Laraque, A.; Filizola, N.; Guyot, J.L.; Seyler, P.; Fritsch, J.M.; Guimarães, V. Sea-tide effects on flows in the lower reaches of the Amazon River. Hydrol. Process. 2009, 23, 3141–3150. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor UE, A.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]






| Reference | Approach | Domain | Time span | Gridded |
|---|---|---|---|---|
| [17] | Water budgetbased on model output | Basins in Europe and USA | 2002–2006 | No |
| [19] | Water budget based on observed data and model output | Amazon and Mississippi basins | 1970–2006 (Amazonas) 1928–2006 (Mississippi) | No |
| [41] | Water budget based on observed and reanalysis data | Basins in several continents | 1992–2005 | No |
| [42] | Reduced optimal interpolation using GRACE data and in situ river level records | Amazon basin | 1980–2008 | Yes |
| [18] | Water budget using GRACE data and model outputs | Amazon basin | 1948–2010 | No |
| [20] | Statistical model using reanalysis data | Global | 1985–2015 | Yes |
| [43] | Physically based modelling and deep learning | India | 2002–2017 | Yes |
| Product—Resolution | MAE (cm) (calib./valid) | CC (calib./valid) | γ (calib./valid) |
|---|---|---|---|
| TWSalt−0.5° | 6.43/6.35 | 0.78/0.79 | 0.77/0.77 |
| TWSalt−1° | 5.9/6.05 | 0.78/0.78 | 0.78/0.75 |
| TWSalt−2° | 5.41/5.58 | 0.82/0.82 | 0.81/0.79 |
| TWSalt−3° | 5.09/5.40 | 0.80/0.78 | 0.79/0.75 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melo, D.d.C.D.; Getirana, A. Radar Altimetry as a Proxy for Determining Terrestrial Water Storage Variability in Tropical Basins. Remote Sens. 2019, 11, 2487. https://doi.org/10.3390/rs11212487
Melo DdCD, Getirana A. Radar Altimetry as a Proxy for Determining Terrestrial Water Storage Variability in Tropical Basins. Remote Sensing. 2019; 11(21):2487. https://doi.org/10.3390/rs11212487
Chicago/Turabian StyleMelo, Davi de C. D., and Augusto Getirana. 2019. "Radar Altimetry as a Proxy for Determining Terrestrial Water Storage Variability in Tropical Basins" Remote Sensing 11, no. 21: 2487. https://doi.org/10.3390/rs11212487
APA StyleMelo, D. d. C. D., & Getirana, A. (2019). Radar Altimetry as a Proxy for Determining Terrestrial Water Storage Variability in Tropical Basins. Remote Sensing, 11(21), 2487. https://doi.org/10.3390/rs11212487