Hyperspectral Pansharpening Based on Spectral Constrained Adversarial Autoencoder

Abstract

Hyperspectral (HS) imaging is conducive to better describing and understanding the subtle differences in spectral characteristics of different materials due to sufficient spectral information compared with traditional imaging systems. However, it is still challenging to obtain high resolution (HR) HS images in both the spectral and spatial domains. Different from previous methods, we first propose spectral constrained adversarial autoencoder (SCAAE) to extract deep features of HS images and combine with the panchromatic (PAN) image to competently represent the spatial information of HR HS images, which is more comprehensive and representative. In particular, based on the adversarial autoencoder (AAE) network, the SCAAE network is built with the added spectral constraint in the loss function so that spectral consistency and a higher quality of spatial information enhancement can be ensured. Then, an adaptive fusion approach with a simple feature selection rule is induced to make full use of the spatial information contained in both the HS image and PAN image. Specifically, the spatial information from two different sensors is introduced into a convex optimization equation to obtain the fusion proportion of the two parts and estimate the generated HR HS image. By analyzing the results from the experiments executed on the tested data sets through different methods, it can be found that, in CC, SAM, and RMSE, the performance of the proposed algorithm is improved by about 1.42%, 13.12%, and 29.26% respectively on average which is preferable to the well-performed method HySure. Compared to the MRA-based method, the improvement of the proposed method in in the above three indexes is 17.63%, 0.83%, and 11.02%, respectively. Moreover, the results are 0.87%, 22.11%, and 20.66%, respectively, better than the PCA-based method, which fully illustrated the superiority of the proposed method in spatial information preservation. All the experimental results demonstrate that the proposed method is superior to the state-of-the-art fusion methods in terms of subjective and objective evaluations.

1. Introduction

Hyperspectral (HS) images captured by sensors under different spectrums have hundreds of narrow spectral channels with detailed spectral information. Because of the rich spectral information, HS images can play a pivotal role in the fields of classification, detection, segmentation, tracking, and recognition [1,2,3,4,5,6]. However, one of the main obstacles in HS imaging is that the dense spectral bands allow a limited number of photographs to arrive at a narrow spectral window on average. To ensure a sufficient signal-to-noise ratio (SNR), long-time exposure is often required, thereby sacrificing spatial resolution [7,8]. All in all, the present research makes a major contribution to obtaining reliable remote sensing images for specific applications to solve the limitations that are caused by spatial resolution [9].

Compared with the HS image, the existing panchromatic (PAN) image is captured by a panchromatic imaging sensor with much higher spatial resolution and SNR [10]. Consequently, the HS pansharpening technique has emerged to reconstruct a high spatial resolution (HR) HS image that fuses a low spatial resolution (LR) HS image with an HR PAN image. This procedure can combine the preponderance and complementary information together on HS and PAN images.

A considerable amount of HS pansharpening methods have been proposed, which can be mainly classified into four categories: multi-resolution analysis (MRA) [11] methods, composition substitution (CS) [12] methods, matrix decomposition methods, and Bayesian-based methods [13,14,15]. The CS-based methods include principal component analysis (PCA) method, the intensity-hue-saturation (IHS) transform method, the Gram–Schmidt (GS) spectral sharpening method [16,17,18], etc. These methods extract the spatial details of the HS image and replace the extracted spatial details with the HR PAN image by employing the inverse transformation, which are fast and easy to implement. However, the results of these methods have consistently shown some noticeable spectral distortion. The MRA-based methods include algorithms such as wavelet transform, Laplacian pyramid (LP), smoothing filter-based intensity modulation (SFIM), the decimated wavelet transform (DWT), Laplacian pyramid, modulation transfer function (MTF), modulation transfer function generalized Laplacian pyramid (MTF-GLP), MTF-GLP with high-pass modulation (MTF-GLP-HPM) [14,19,20,21,22], etc. By injecting obtained details from the PAN image into the HS images, the MRA approaches can keep good spectral information but often contain too many spatial details and suffer from spatial distortions, such as ringing artifacts. In recent years, the matrix decomposition-based methods and Bayesian-based methods are proposed. The coupled non-negative matrix factorization (CNMF) [1,23] and non-negative sparse coding (NNSC) are typical algorithms of matrix decomposition. The fused image is generated by a non-negative matrix factorization (NMF) [24] model to realize the fusion of HS and PAN images under some constraints to estimate endmember and abundance matrices. Moreover, Lanaras et al. adopted a projected gradient method into the alternate updates of the endmember and abundance matrices [25]. Although the matrix decomposition based-methods perform well, they separate the relationship between the spatial and spectral information, which may lead to spatial or spectral distortion. Bayesian approaches include Bayesian sparsity promoted Gaussian prior (Bayesian Sparse), Bayesian sparse representation (BSR) [26], HySure [27], Bayesian naive Gaussian prior (Bayesian Naive), etc. These methods consider the problem of HS pansharpening as a distinct probabilistic framework. Then, an appropriate prior distribution is used to obtain the fused HS image, and the probabilistic framework is regularized. The performance in repair and maintenance is excellent in Bayesian methods, but they have accentuated the problem of high computational complexity and the requirement of solid prior information to achieve pleasurable results, leading to some limitations in practical application.

In recent years, inspired by the successful application of deep neural networks (DNNs) in image processing, convolutional neural networks (CNNs) have been used in image super-resolution (SR) [27,28,29]. The design and application of SRCNN [30], the first SR neural network model in the gray image, and RGB image are of great significance in the field of SR. Based on SRCNN, different DNN structures are proposed, such as EDSR [31,32], DRCN [33], VDSR [34], LapSRN [35], SRGAN [36], SRMD [37], etc. These DNN methods for a gray level or RGB images can be directly applied to the HS image band by band. The existing research on the DNN model is specifically designed for the advantages of DNN in HS pansharpening. Most of them were initially proposed to fuse MS and PAN images [38]. Qi et al. proposed a model-based method for the fusion of LR HS image and HR multispectral (MS) image [39]. This method integrates the LR image observation model with low-rank knowledge to construct a new MS/HS fusion model. Firstly, the approximate series method is used to design the iterative algorithm to solve the model. Then, the algorithm is extended to construct a deep network, and the approximation operator and model parameters can be learned by using CNN to achieve good results. Even so, it regards pansharpening as a black-box deep learning problem without ultimate consideration of spectral and spatial protection [40]. With a supervised network, the method requires plenty of computational costs for the input of the high-dimensional HS images. At the same time, the limitation of training samples is still a problem which remains to be solved. Recently, a number of CNN-based methods have sought to estimate performance on data sets with fewer spectral bands, but when the bandwidth reaches the order of HS image, the computation is heavy, the memory requirement of GPU is high, and the operation is difficult.

In this paper, to address the above problems, we propose a new HS pansharpening method based on spectral constrained adversarial autoencoder (SCAAE) inspired by our previous work [41]. The proposed method was used for HS pansharpening for the first time effectively acquiring the spatial information of HS image and improving the quality of the fused image. In order to reduce spectral distortion, we have added spectral constraints in AAE. Compared with the state-of-the-art methods, the proposed method improves the ability of spatial information enhancement and spectral information preservation. We conduct experiments on different data sets and make further efforts to illustrate the superior performance of the proposed SCAAE based HS pansharpening method.

In summary, the main novelties and contributions of the proposed HS pansharpening method are concluded as follows:

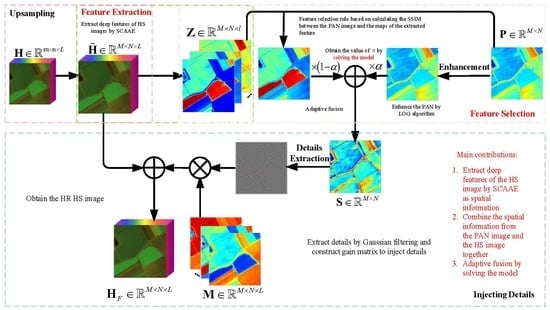
• We first propose SCAAE based HS pansharpening method to extract features and obtain spatial information of HS images. Especially for spectral information preservation, the spectral constraints are added into the loss function of the network to reduce spectral distortion further.
• An adaptive selection rule is constructed to select an effective feature that can well represent the up-sampled HS image. In particular, the structural similarity is introduced to compare the similarity of the PAN and the extracted features of the up-sampled HS image.
• We construct an optimization equation to solve the proportion of HS and PAN images in the final fusion framework. The experiments show that the proposed SCAAE pansharpening method is superior to the existing state-of-the-art methods.

The following part of this paper is divided into six sections. Section 2 reviews the related work. Section 3 describes the proposed method. Section 4 is devoted to experiments and results. Section 5 is about the discussion and analysis. In Section 6, we make conclusions.

2. Related Work

In this section, the frequently used methods for HS pansharpening are reviewed, and their existing challenges are analyzed. In a traditional way, the HS pansharpening problem can be written as:

$$\begin{array}{c}\hfill min{f}_1(\mathbf{X},\mathbf{Y})+f_2\left(\mathbf{X},\mathbf{P}\right).\end{array}$$

(1)

In the first term, $f_1$ is the mapping relationship between the down-sampled HS image $\mathbf{Y}$ and the pansharpened HS image $\mathbf{X}$, which is used to minimize spectral distortion. In the second term, $f_2$ is the mapping relationship between the PAN image $\mathbf{P}$ and the pansharpened HS image $\mathbf{X}$. This part helps preserve spatial information.

Yang et al. [42] proposed a deep network-based method called PanNet, which automatically learns the mapping purely from data and incorporates problem-specific knowledge into the deep learning framework and focuses on two main aspects of fusion problem: spatial and spectral preservation. In this method, Resnet is trained to obtain high-frequency information by a high-pass filter. Then, the high-frequency details are injected into the up-sampled HS image. However, the spectral constraint of PanNet is constructed from the output of the spatial preserving network and the original HS image, which means that the spectral preservation in PanNet depends on spatial preservation. It is an indirect condition which may lead to sub-optimal preservation results. In addition, the quality of fusion mainly depends on the training result of the PanNet, leading to a lack of stability and robustness.

Hence, we proposed the SCAAE based pansharpening method. The work related to it is adversarial training and adversarial autoencoders, which are described in more detail below.

2.1. Adversarial Training

As described by Goodfellow et al. [43], adversarial training involves learning the mapping from latent samples $\mathbf{z}$ to data samples $\mathbf{x}$. Adversarial training is an iterative training of two competitive models: the generator model G and the discriminator model D. The generator is fed with input samples $\mathbf{x}$ and is optimized to generate the latent feature that fools the discriminator with $\mathbf{z}\sim p\left(\mathbf{z}\right)$ until $\mathbf{z}\sim q\left(\mathbf{z}\right)$ can be considered as coming from the imposed prior distribution $\mathbf{z}\sim p\left(\mathbf{z}\right)$ on the latent feature space. Meanwhile, the discriminator is fed with the latent samples $\mathbf{z}\sim q\left(\mathbf{z}\right)$ from the output of the generator and the samples $\mathbf{z}\sim p\left(\mathbf{z}\right)$ which obey the target aggregated posterior distribution. It is trained to correctly predict whether the samples are from the imposed prior distribution or the generated latent feature, and then give the judgment of truth and falsity to update the parameters of the generator. The following min-max objective can achieve the discussed competitive training:

$$\begin{array}{c}\hfill \underset{G}{min}\underset{D}{max}{E}_{\mathbf{z}\sim q\left(\mathbf{z}|\mathbf{x}\right)}\left[logD\left(\mathbf{z}\right)\right]+E_{\mathbf{z}\sim p\left(\mathbf{z}\right)}\left[log\left(1-D\left(G\left(\mathbf{z}\right)\right)\right)\right],\end{array}$$

(2)

where $\mathbf{z}$ is output samples of the generator. $\mathbf{z}\sim p\left(\mathbf{z}\right)$ denotes a target probability distribution. $D\left(\mathbf{z}\right)$ is the discriminative model. $q\left(\mathbf{z}\right|\mathbf{x})$ represents both the encoding model and generative model.

2.2. Adversarial Autoencoders

In AAE [44] network, adversarial learning ideas are added to the autoencoder (AE) model to accurately approximate the potential feature space on an arbitrary prior basis. In [45], $q\left(\mathbf{z}\right|\mathbf{x})$ is specified by a neural network whose input is $\mathbf{x}$ and output is $\mathbf{z}$, which allows $q\left(\mathbf{z}\right|\mathbf{x})$ to have arbitrary complexity, unlike the variational autoencoder (VAE) [46] where the structure of $q\left(\mathbf{z}\right|\mathbf{x})$ is usually limited to a multivariate Gaussian. An analytical solution of Kullback–Leibler (KL) divergence is required as the choice of the prior distribution, and posterior distribution is limited. However, a posterior distribution in AAE does not need to be defined analytically, and it can match $q\left(\mathbf{z}\right|\mathbf{x})$ to several different priors $p\left(\mathbf{z}\right)$. The reason is that AAE can learn a model through adversarial training, which can match samples with any complex target distribution, avoiding the need to compute a KL divergence analytically.

AAE accepts a dual training goal, including a traditional reconstruction error and an adversarial training criterion that matches the potential representation with an arbitrary prior distribution. To be specific, both the reconstruction error and the discriminators make the latent feature space distribution approximate the imposed prior contribution for updating the encoder. In AAE, $q\left(\mathbf{z}|\mathbf{x}\right)$ plays a double rule in both the encoder of the autoencoder framework and the generator in an adversarial framework. Thus, the AAE framework learns the aggregate posterior distribution $q\left(\mathbf{z}\right)$, which can be described as follows:

$$\begin{array}{c}\hfill q\left(\mathbf{z}\right)={\int }_{x}q\left(\mathbf{z}|\mathbf{x}\right)p\left(\mathbf{x}.\right)d\mathbf{x}\end{array}$$

(3)

The discriminator of AAE is trained to distinguish the latent samples $\mathbf{z}\sim p\left(\mathbf{z}\right)$ from the probabilistic encoder conditioned on the samples $\mathbf{z}\sim q\left(\mathbf{z}|\mathbf{x}\right)$. The cost function for training the discriminator D is:

$$\begin{array}{c}\hfill Los{s}_D=-\frac{1}{K}\sum _{i=0}^{K-1}logD\left({\mathbf{z}}_i\right)-\frac{1}{K}\sum _{j=K}^{2K-1}log\left(1-D\left({\mathbf{z}}_j\right)\right),\end{array}$$

(4)

where ${\mathbf{z}}_i\sim p\left(\mathbf{z}\right)$, ${\mathbf{z}}_j\sim q\left(\mathbf{z}|\mathbf{x}\right)$. K is the size of the training batch.

To match $q\left(\mathbf{z}\right)$ to an arbitrarily chosen prior $p\left(\mathbf{z}\right)$, the adversarial training is implemented. The cost function for matching $q\left(\mathbf{z}|\mathbf{x}\right)$ to prior $p\left(\mathbf{z}\right)$ is:

$$\begin{array}{c}\hfill Los{s}_G=\frac{1}{K}\sum _{i=0}^{K-1}log\left(1-D\left({\mathbf{z}}_i\right)\right).\end{array}$$

(5)

3. Proposed Method

Let $\tilde{\mathbf{H}}\in {\mathbb{R}}^{M\times N\times L}$ represent the up-sampled HS image, in which L is the number of bands and $M\times N$ is the number of spatial pixels. Let $\mathbf{Z}\in {\mathbb{R}}^{M\times N\times l}$ denote the extracted feature of $\tilde{\mathbf{H}}$. The final selected feature is denoted by ${\mathbf{Z}}_s\in {\mathbb{R}}^{M\times N}$.

Figure 1 shows the overall flowchart of our proposed approach. The proposed method is described in three parts: feature extraction, feature selection, and solving the model. The detailed description is as follows. The overall model can be expressed by the following equation:

$$\begin{array}{c}\hfill W={∥{\mathbf{H}}_R-\left(\tilde{\mathbf{H}}+\mathbf{M}\otimes \left(\alpha {\mathbf{P}}_{\mathrm{e}}+\left(1-\alpha \right){\mathbf{Z}}_s\right)-f_{Gauss}\left(\alpha {\mathbf{P}}_{\mathrm{e}}+(1-\alpha ){\mathbf{Z}}_s\right)\right)∥}_F^2,\end{array}$$

(6)

where ${∥·∥}_F$ denotes the Frobenius norm. $\mathbf{M}$ represents the gains matrix. The symbol ⊗ denotes element-wise multiplication. $\tilde{\mathbf{H}}$ and ${\mathbf{H}}_R$ represent the up-sampled HS image and the reference HS image, respectively. The selected feature and enhanced PAN image are denoted by ${\mathbf{Z}}_s$, and ${\mathbf{P}}_{\mathrm{e}}$. $f_{Gauss}\left(·\right)$ represents the Gaussian filter function. For convenience, we denote the combined PAN as:

$$\begin{array}{c}\hfill \mathbf{S}=\alpha {\mathbf{P}}_{\mathrm{e}}+(1-\alpha ){\mathbf{Z}}_s\end{array}$$

(7)

and its Gaussian filtering version is represented as:

$$\begin{array}{c}\hfill {\mathbf{S}}_G=f_{Gauss}\left(\alpha {\mathbf{P}}_{\mathrm{e}}+\left(1-\alpha \right){\mathbf{Z}}_s\right).\end{array}$$

(8)

Thus, the model can be described as:

$$\begin{array}{c}\hfill \mathrm{W}={∥{\mathbf{H}}_R-\left(\tilde{\mathbf{H}}+\mathbf{M}\otimes \left(\mathbf{S}-{\mathbf{S}}_G\right)\right)∥}_F^2.\end{array}$$

(9)

In general, the complete HS image is used for HS pansharpening because the information of HS image is rich and complex, and it contains abundant pixels. Nevertheless, the effective pixels that can represent the spatial information of HS images are limited, that is to say, there is a certain amount of redundant information in HS images. Therefore, we reduce the dimension of HS images by feature extraction and obtain low-dimensional spatial features to represent the effective information on HS images and reduce the computational cost. Furthermore, traditional feature extraction methods only extract shadow features and probably cause the loss of effective information as well as image distortion. It is worth noting that feature extraction methods based on deep learning can better mine deep spatial features. Through deep learning methods based on DNN, the obtained features can maintain certain invariance and contain higher-level semantic information, which effectively narrow the gap between the bottom features and the high-level semantics [47,48]. It is worthwhile exploring a specifically HS pansharpening method based on DNN that is practical and efficient to the data sets [49,50,51,52]. In this paper, we propose an unsupervised deep learning pansharpening method based on SCAAE to achieve feature extraction. More details are explained in Section 3.1, Section 3.2, Section 3.3 and Section 3.4.

3.1. Feature Extraction

In this section, we talk about the motivation and process of feature extraction by SCAAE. According to our research, the existing methods only consider the spatial information of the PAN image and ignore the spatial information of HS images. Furthermore, there are some traditional methods generally used to extract features of HS images to represent the spatial information. It is not satisfying that most of them are shallow features that can not fully express the comprehensive information of HS images [53,54,55]. To solve the problem, in this paper, we propose the SCAAE based pansharpening method to mine deeper features. The specific operations are as follows.

The three-dimensional HS image is converted to a two-dimensional vector and sent to the SCAAE network. The input $\tilde{\mathbf{H}}$ can be interpreted as $MN$ vectors with L dimensions, which can be denoted as $\tilde{\mathbf{H}}=\left[{\mathbf{h}}_{\mathbf{1}},{\mathbf{h}}_{\mathbf{2}},\dots ,{\mathbf{h}}_{MN}\right]$. The weights and biases of the encoder and the decoder are operated by linear operations to obtain the reconstructed result $\widehat{\mathbf{H}}=\left[{\widehat{\mathbf{h}}}_{\mathbf{1}},{\widehat{\mathbf{h}}}_{\mathbf{2}},\dots ,{\widehat{\mathbf{h}}}_{MN}\right]$. In SCAAE, a suitable constraint is added to the latent feature space in loss function, which is based on spectral angle distance (SAD) so that the spectral consistency can be well kept. In the encoder, which is also called a generator, the hidden layer consists of two fully connected layers, and the activation function is LeakyRelu [56]. The ReLU may lead to dead nodes when training for a positive response is kept, while negative responses are suppressed by setting them to zero. The LeakyReLU overcomes the drawback when negative responses are suppressed by setting them to a small negative slope, such as 0.2. The network structure of the decoder is similar to the encoder, which consists of two fully connected layers, and the activation functions are LeakyRelu and Sigmoid. As for the discriminator, it contains a fully connected layer and uses LeakyRelu as the activation function. We set the learning rate as ${10}^{-4}$, and the training batch size is set to the same number as the spatial dimension of the input up-sampled HS image. The loss function of the whole network includes the loss function of autoencoder, generator, and discriminator. Then, the optimization process is optimized by using the Adam algorithm. More details of the training are discussed as follows.

The upsampled HS image is sent as input to the SCAAE network, which is iteratively trained to obtain the feature. The training process consists of two steps. Firstly, the autoencoder is trained to perform image reconstruction, which enables the decoder to recover the original image from the latent samples generated by the encoder. Secondly, the discriminator and generator begin adversarial learning.

In SCAAE, $q\left(\mathbf{z}|\mathbf{h}\right)$ represents both the encoder of the autoencoder framework and the generator in an adversarial framework. The generator G is trained to generate latent samples to deceive the discriminator D. When $p\left(\mathbf{z}\right)$ is more similar to $q\left(\mathbf{z}\right)$, the training effect is better. As a result, the feature of the upsampled HS image is obtained, and spatial information is well extracted. The reconstruction error of the SCAAE can be expressed in:

$$\begin{array}{c}\hfill Los{s}_{auto}={∥\tilde{\mathbf{H}}-\widehat{\mathbf{H}}∥}_2,\end{array}$$

(10)

where $\tilde{\mathbf{H}}$ and $\widehat{\mathbf{H}}$ represent the input image and the reconstructed image, repectively. The error between the reconstructed HS image and the input HS image is expressed in the form of norm, and we can measure the reconstruction and feature extraction quality of the SCAAE network.

The loss function for matching $q\left(\mathbf{z}|\mathbf{h}\right)$ to prior $p\left(\mathbf{z}\right)$ is described as follows:

$$\begin{array}{c}\hfill Los{s}_G=\frac{1}{K}\sum _{i=0}^{K-1}log(1-D\left({\mathbf{z}}_i\right)).\end{array}$$

(11)

The discriminator is trained to distinguish the latent samples $\mathbf{z}\sim p\left(\mathbf{z}\right)$ from the probabilistic encoder conditioned on the input samples $q\left(\mathbf{z}|\mathbf{h}\right)$. The cost function used to train the discriminator D is:

$$\begin{array}{c}\hfill Los{s}_D=-\frac{1}{K}\sum _{i=0}^{K-1}logD\left({\mathbf{z}}_i\right)-\frac{1}{K}\sum _{j=K}^{2K-1}log(1-D\left({\mathbf{z}}_j\right)),\end{array}$$

(12)

where ${\mathbf{z}}_i\sim p\left(\mathbf{z}\right)$, ${\mathbf{z}}_j\sim q\left(\mathbf{z}|\mathbf{h}\right)$. K is the size of the training batch.

We improve the structure of AAE by adding spectral constraints in the loss function. By calculating the difference of spectral angle vector between the input image $\tilde{\mathbf{H}}$ and reconstructed image $\widehat{\mathbf{H}}$, the spectral constraint loss is defined:

$$\begin{array}{c}\hfill Los{s}_{SAD}=\frac{1}{MN}·\frac{1}{\pi }\sum _{i=1}^{MN}arccos\left(\frac{{\mathbf{h}}_i·{\widehat{\mathbf{h}}}_i}{{∥{\mathbf{h}}_i∥}_2·{∥{\widehat{\mathbf{h}}}_i∥}_2}\right),\end{array}$$

(13)

where $MN$ is the total pixels in the HS image. By adding the spectral constraints based on SAD to reduce spectral distortion, the total loss function in SCAAE can be described as follows:

$$\begin{array}{c}\hfill Loss=L\mathrm{o}s{s}_G+Los{s}_D+Los{s}_{SAD}.\end{array}$$

(14)

When the total loss is minimized, we obtain the feature of the HS image. Let $\mathbf{Z}$ denote the extracted feature of up-sampled HS image $\tilde{\mathbf{H}}$. Let l denote the total number of the feature. Therefore, $\mathbf{Z}$ can be expressed by:

$$\begin{array}{c}\hfill \mathbf{Z}=\left[{\mathbf{Z}}_1,{\mathbf{Z}}_2,\dots ,{\mathbf{Z}}_l\right]\end{array}$$

(15)

for $i=1,2,\dots ,l$. ${\mathbf{Z}}_i$ represents the ith feature map.

The process of feature extraction is illustrated in Figure 2.

3.2. Feature Selection

Aiming at the problem of insufficient spatial information and spectral distortion, we select the feature based on the structural similarity index (SSIM) by our selection rule in the adaptive fusion approach. We denote $\mathbf{Z}$ as the extracted feature of up-sampled HS image $\tilde{\mathbf{H}}$. l is the number of feature maps. Thus, $\mathbf{Z}$ can also be expressed by $\mathbf{Z}=\left[{\mathbf{Z}}_1,{\mathbf{Z}}_2,\dots ,{\mathbf{Z}}_l\right]$. The ith map of the feature is denoted by ${\mathbf{Z}}_i$. To gain less spectral distortion and complete spatial information, we find the SSIM value of feature maps and PAN image, and then take out the feature map whose index is the biggest. The feature map with the largest SSIM value represents the one most similar to the PAN image. Since the PAN image has sufficient spatial information, the feature map with the largest SSIM value is selected as the spatial information of the up-sampled HS image. Accordingly, the spatial information used for fusion is complete. The selection rule is based on the following equation:

$$\begin{array}{c}\hfill max\left[\frac{\left(2{\mu }_{{\mathbf{Z}}_i}{\mu }_{\mathbf{P}}+c_1\right)\left(2{\sigma }_{{\mathbf{Z}}_i\mathbf{P}}+c_2\right)}{\left({\mu }_{{\mathbf{Z}}_i}^2+{\mu }_{\mathbf{P}}^2+c_1\right)\left({\sigma }_{{\mathbf{Z}}_i}^2+{\sigma }_{\mathbf{P}}^2+c_2\right)}\right],\end{array}$$

(16)

where ${\mathbf{Z}}_i$ and $\mathbf{P}$ represent the ith feature map of extracted feature $\mathbf{Z}$ and the PAN image, respectively. ${\mu }_{{\mathbf{Z}}_i}$ is the mean of ${\mathbf{Z}}_i$. ${\mu }_{\mathbf{P}}$ is the mean of $\mathbf{P}$. ${\sigma }_{{\mathbf{Z}}_i}^2$ is the variance of ${\mathbf{Z}}_i$. ${\sigma }_{\mathbf{P}}^2$ is the variance of $\mathbf{P}$. ${\sigma }_{{\mathbf{Z}}_i\mathbf{P}}$ is the covariance between ${\mathbf{Z}}_i$ and $\mathbf{P}$. $c_1={\left(0.01\times C\right)}^2$ and $c_2={\left(0.03\times C\right)}^2$ are stable constants. C is the dynamic range of pixel values. The bigger SSIM value means a better result. The optimal value is 1, representing the compared two images being exactly similar to each other [57,58]. The feature map with the most significant SSIM value is denoted as ${\mathbf{Z}}_s$.

Therefore, we select ${\mathbf{Z}}_s$ whose spatial structure is most similar to the spatial structure of the PAN image, and use it to represent the spatial information of the HS image to improve the spatial information of the fusion process and reduce the spatial distortion.

3.3. Solving the Model

As stated above, the overall problem can be described by Equation (6). In this part, we further explain our model and talk about the solution. There are three main steps in our model: obtaining the combined PAN image, injecting details, and solving the optimization equation. The specific processes are described in detail in Section 3.3.1, Section 3.3.2 and Section 3.3.3.

3.3.1. Obtaining the Combined PAN Image

The Laplacian of Gaussian (LOG) image enhancement algorithm is applied to the PAN image to improve the robustness to noise and discrete points to make the spatial information of the PAN image clearer. Firstly, Gaussian convolution filtering is used to remove the noise, and then the Laplacian operator is used to enhance the detail of the denoised image. The algorithm is described as:

$$\begin{array}{c}\hfill {\mathbf{P}}_{\mathrm{e}}=\mathbf{P}+\omega \left[\mathbf{P}\ast f_{LOG}\left(x,y\right)\right],\end{array}$$

(17)

where ${\mathbf{P}}_{\mathrm{e}}$ is the enhanced PAN image. $f_{LOG}\left(x,y\right)$ is the kernel function of LOG operator. $\omega$ is a constant. ∗ denotes the convolution operator.

Spectral and spatial information of HS and PAN images need to be considered simultaneously because of different and complementary spatial information for the same scene. Consequently, the filtered image and the PAN image are adaptively integrated, as described in Equation (7). Finally, the combined PAN image is obtained, and the adequacy of space information is guaranteed.

3.3.2. Injecting Details

Although the adaptive fusion approach successfully obtains the spatial information from the feature map of the interpolated HS image and the detail layer of the enhanced PAN image, some spatial and spectral information of the flat region whose pixel values are similar to the surrounding pixel values has not been enhanced. As a result, some details should be injected to improve the appearance further. In Equation (8), a Gaussian filter is performed on the combined PAN image to remove the high-frequency component so that we can obtain the low-frequency component. Then, the details are acquired when the low-frequency component from the original PAN image is subtracted. The spatial details are obtained by making a difference to the images before and after filtering according to the following formula:

$$\begin{array}{c}\hfill \mathbf{I}=\left(\alpha {\mathbf{P}}_{\mathrm{e}}+\left(1-\alpha \right){\mathbf{Z}}_s\right)-f_{Gauss}\left(\alpha {\mathbf{P}}_{\mathrm{e}}+\left(1-\alpha \right){\mathbf{Z}}_s\right).\end{array}$$

(18)

The spatial information $\mathbf{I}$ is injected into the respective bands of the interpolated image through the gains matrix to generate a fused HR HS image:

$$\begin{array}{c}\hfill {\mathbf{H}}_F^k={\tilde{\mathbf{H}}}^k+{\mathbf{M}}^k\otimes \mathbf{I},\end{array}$$

(19)

where ${\mathbf{H}}_F^k$ represents the kth band of the merged HS image. The gains matrix is ${\mathbf{M}}^k=\beta \frac{{\tilde{\mathbf{H}}}^k}{\left(1/\phantom{1L}L\right){\sum }_{k=1}^L{\tilde{\mathbf{H}}}^k}$. $k=1,2,\dots ,L$. L is the band number of the reference HS image. ${\tilde{\mathbf{H}}}^k$ is the kth band of the up-sampled HS image. ${\mathbf{M}}^k$ is the kth band of the gains matrix.

3.3.3. Solving the Optimization Equation

As mentioned above, ${\mathbf{Z}}_s$, ${\mathbf{P}}_{\mathrm{e}}$, and $\mathbf{M}$ are defined or learned by our proposed method. Therefore, only $\alpha$ remains unknown in Equation (6). We obtain the parameter values by separately solving the equations which force the partial derivative of $\alpha$ and $\beta$ to zero. Firstly, we have:

$$\begin{array}{c}\hfill \frac{\partial W}{\partial \alpha }=\frac{\partial W}{\partial \mathbf{S}}·\frac{\partial \mathbf{S}}{\partial \alpha }=0.\end{array}$$

(20)

By letting the first factor equal to zero, it can be written as:

$$\begin{array}{c}\hfill \frac{\partial W}{\partial \mathbf{S}}=\left\{{\mathbf{H}}_R-\left\{\tilde{\mathbf{H}}+\mathbf{M}\otimes \left[\mathbf{S}-f_{Gauss}\left(\mathbf{S}\right)\right]\right\}\right\}·\mathbf{M}\otimes \left(1-\frac{\partial f_{Gauss}}{\partial \mathbf{S}}\right)=0.\end{array}$$

(21)

To simplify the equation, we denote:

$$\begin{array}{c}\hfill {\mathbf{s}}_{ij}=\mathbf{S}-f_{Gauss}\left(\mathbf{S}\right)\end{array}$$

(22)

for $i=1,2,\dots M$, $j=1,2,\dots N$. Then, we have:

$$\begin{array}{c}\hfill \sum _{k=1}^L{\mathbf{H}}_R\left[i,j,k\right]\mathbf{M}\left[i,j,k\right]=\sum _{l=1}^L\left(\tilde{\mathbf{H}}\left[i,j,k\right]+\mathbf{M}\left[i,j,k\right]·{\mathbf{s}}_{ij}\right).\end{array}$$

(23)

Therefore, the value of ${\mathbf{s}}_{ij}$ can be obtained:

$$\begin{array}{c}\hfill {\mathbf{s}}_{ij}=\frac{{\displaystyle \sum _{k=1}^L}{\mathbf{H}}_R\left[i,j,k\right]\mathbf{M}\left[i,j,k\right]-\tilde{\mathbf{H}}\left[i,j,k\right]}{{\displaystyle \sum _{k=1}^L}\mathbf{M}\left[i,j,k\right]}.\end{array}$$

(24)

As stated earlier, we can obtain another expression of ${\mathbf{s}}_{ij}$:

$$\begin{array}{c}\hfill {\mathbf{s}}_{ij}=\alpha {\mathbf{P}}_{\mathrm{e}}+(1-\alpha ){\mathbf{Z}}_s-f_{Gauss}\left[\alpha {\mathbf{P}}_{\mathrm{e}}+(1-\alpha ){\mathbf{Z}}_s\right].\end{array}$$

(25)

Then, we define a new function of the input x:

$$\begin{array}{c}\hfill f_d\left(x\right)=x-f_{Gauss}\left(x\right).\end{array}$$

(26)

Thus, the equation of $\alpha$ can be formed as follows:

$$\begin{array}{c}\hfill \alpha \left[f_d\left({\mathbf{P}}_{\mathrm{e}}\right)-f_d\left({\mathbf{Z}}_s\right)\right]+f_d\left({\mathbf{Z}}_s\right)={\mathbf{s}}_{ij}.\end{array}$$

(27)

Finally, we obtain the solution of Equation (27):

$$\begin{array}{c}\hfill \alpha =\frac{{\mathbf{s}}_{ij}-f_d\left({\mathbf{Z}}_s\right)}{f_d\left({\mathbf{P}}_{\mathrm{e}}\right)-f_d\left({\mathbf{Z}}_s\right)}.\end{array}$$

(28)

3.4. Performance Evaluation

After the model is established and solved successfully, four widely used reference indexes are adopted for performance evaluation, including CC, SAM, RMSE, and ERGAS. The interpretation of the indexes is described in the part of the experiment. The fusion quality of various HS pansharpening methods was compared and assessed by the indexes of Cross-Correlation (CC) [59], spectral angle mapper (SAM) [14], root mean square error (RMSE) [60], and erreur relative to global adimensionnellede synthse (ERGAS) [61]. CC is a spatial index evaluating the spatial distortion degree. The ideal value is 1. Larger CC value indicates better fusion quality. SAM is a spectral indicator that measures spectral distortion between the HS image and the fused image. RMSE is the global index that appraises the spatial and spectral fusion qualities. ERGAS is also a global quality index, evaluating the spatial and spectral distortion. The optimal value of SAM, RMSE, and ERGAS are 0. The smaller the value is, the better the fusion performance. The simulated HS image and the simulated PAN image can be generated from a given reference HS image. Subsequently, the fusion results can be obtained from the simulated HS image and the simulated PAN image. The fusion results are compared with the available reference HS image to evaluate the objective quality of the synthetic data sets.

4. Experimental Results and Discussion

In this part, we compare the fusion quality of the proposed HS pansharpening method with ten state-of-the-art algorithms, which are SFIM, MTF-GLP, MTF-GLP-HPM, GS, GSA, GFPCA, CNMF, Lanaras’s, HySure, and FUSE.

4.1. Data Set

To evaluate the effectiveness of the proposed HS pansharpening method, we perform experiments on four simulated HS data sets, i.e., Moffett Field data set [59], Salinas Scene data set, Pavia University data set, and Chikusei data set. The comparative experiments are conducted both quantitatively and visually.

The first data set is the Moffett field data set, acquired by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) sensor [62], which can provide the HS image 224 bands in the spectral range of 400–2500 nm. Water absorption bands and damaged bands are discarded, and 176 bands are used for the experiment. The dimensions of the test HS image are 75 × 45 with a spatial resolution of 5.2 m, and the size of the test PAN image is 300 × 180 with a spatial resolution of 1.3 m.

The second data set is the Salinas Scene data set, which is also obtained by the AVIRIS sensor. This data set includes vegetables, bare soils, and vineyard fields. There are 224 bands covering the spectral range of 400–2500 m. Twenty water absorption bands and damaged bands are discarded, and 204 bands are used for the experiment. The dimensions of the test HS image are 40 × 40 with a spatial resolution of 1.3 m, and the size of the test PAN image is 200 × 200 with a spatial resolution of 5.2 m.

The third data set is the Pavia University data set obtained by the Reflective Optics System Imaging Sensor (ROSIS) over Pavia, Italy. The HS image consists of 115 bands covering the spectral range of 400–900 nm. There are 103 bands applied to experimentation. The dimension of the test HS image is 50 × 50 pixels with a spatial resolution of 6.5 m, and the size of the test PAN image is 200 × 200 with a spatial resolution of 1.3 m.

The fourth data set is the Chikusei data set. The airborne HS data set was taken by Headwell Visible and Near-Infrared series C (VNIR-C) imaging sensor over agricultural and urban areas in Chikusei, Ibaraki, Japan. The HS data set has 128 bands in the spectral range of 363–1018 nm. The scene consists of 2517 × 2235 pixels, and the ground sampling distance is 2.5 m. The dimension of the test HS image is 150 × 150, and the size of the test PAN image is 600 × 600.

The Moffett Field data set, Salinas Scene data set, Pavia University data set, and Chikusei data set are all simulated data sets. According to the Wald’s protocol, given the reference HS image, simulated HS images and simulated PAN images can be obtained. Moreover, the fusion result is generated by fusing the simulated PAN image and HS image. To evaluate the objective quality of the simulated data sets, these fusion results were compared with original reference HS images.

4.2. Experimental Setup

To evaluate the sensitivity of the SCAAE to its key parameters in pansharpening and make sure the superiority of the final fusion results, we run the SCAAE for different values of the related parameters, including the number of the hidden nodes in each layer, the depth, the pattern of the loss function, activation function, learning rate, batch size, and epochs. By trial and error, the number of hidden nodes in the last layer and the depth of the network are verified to have the most important effect on pansharpening results. Precisely speaking, the impact of different parameter settings on the fusion performance, which can be represented by the CC value and SAM value, is conducted based on the variable controlling approach with the others fixed. The above-mentioned factors that affect the fusion result are independent of each other. The influence of the changed factor on fusion can be seen clearly by changing only one factor at a time and controlling the remaining factors to remain unchanged. With the evaluation of SAM and CC indicators, the most favorable parameter setting scheme for the fusion results is obtained. More details are as follows.

In order to meet the requirement of the abundance of the spectral information, the number of hidden nodes in the first two layers is set to 500 by capturing rich features of the input. Figure 3 plots the CC value between the input HS image and the generated HR HS image with the varying number of hidden nodes in the third layer. As Figure 3 shows, for most of the data sets, the proposed method achieves the best CC value when the number of hidden nodes in the last layer is set to 30. That is to say, the dimension of the extracted feature is 30 to achieve optimal pansharpening performance. Notably, though the CC(0.9300 for the Pavia University data set) is smaller than any others when the number of hidden nodes is 30 at the value of 0.9300, the results are approximate to the ideal value under the same conditions (0.9807, 0.9684, and 0.9565 for Moffett, Salinas, and Chikusei data sets, respectively). Furthermore, we set the depth to 3 to evaluate the input of hidden nodes to SAM. In Figure 3b, it can be seen that the SAM value at the number of 30 is much lower than those obtained at the other numbers, which is consistent with the CC value. Moreover, the performance declines when the number is smaller than 30 for all the tested data sets.

As for the depth of the network, we systematically vary the parameter setting one by one under the precondition of the parameter above and report the CC and SAM value. Figure 3c,d studies the effect of depth of the proposed method on CC and SAM values. Similarly, in order to study the effect of a single variable on the results, we set the number of hidden nodes in the last layer to 30. CC reflects the geometric distortion specially and shows an interesting trend, which reflects the spatial information effectively infected in each process. The CC value for the Salinas Scene data set remains stable as the number of depths varies from 1 to 5. For the Moffett Field and Chikusei data sets, the CC value decreases rapidly as the argument is changed from 3 to 4, while there is an obvious increase from 3 to 4 for the Pavia University data set. As a result, the depth is set to 3 by the comprehensive analysis of the proposed method in the experiments of the four data sets.

As can be seen from Figure 3d, although the values of SAM are very close under different depth settings for Pavia University and Chikusei data sets, the SAM achieves a lower level under the condition of three depth for the Moffett Field and Salinas Scene data sets. Therefore, the proposed method achieves a lower SAM value under the condition of ensuring the preservation of spectral information. From Figure 3c,d, we can conclude that, when the depth is set to 3, the performance achieves the best. While the depth is set to 1 or 5, the values of CC are smaller, and the value of SAM is larger than the condition of 3. Hence, the experiment results and analysis prove that, when the depth of the network is set to 3, the performance of the whole network achieves the most satisfactory.

In addition, the learning rate, weight decay, batch size, and epoch mainly influence the speed of converging. Through fine-tuning, we empirically find that, when the learning rate is set to ${10}^{-4}$, and the decay is set to 0.9, the network converges faster. Considering the trend of the CC and SAM value, we choose 30 as the number of hidden nodes and three as the depth of the network for all data sets in the following experiments.

To illustrate the process of feature extraction intuitively, the intermediate results of hidden nodes extracted by the SCAAE are shown visually in Figure 4 with parameters optimizing performance.

All experiments were performed in the Matlab (R2019a) environment on a server with CPUs: Intel (R) Core (TM) i5-7200U CPU@ 2.70 GHz, an Nvidia K80 GPU and 128 GB memory.

4.3. Component Analysis

In this subsection, the objective results of the proposed method are provided to validate the effect of the essential components step by step. Compared with the existing well-performed methods, the most outstanding advantage of the proposed method is that it not only considered the spatial information of the PAN image but also extracted deep features of HS image as the supplement spatial information through SCAAE. Meanwhile, the method extracts deep features rather than shadow features extracted by traditional methods, which promotes the fusion results very well.

Thus, the effects of significant processing components are analyzed, i.e., deep feature extraction from the HS image from the perspective of objective experimental results on the four tested data sets. In the proposed SCAAE based HS pansharpening model, ${\mathbf{Z}}_s$ represents the selected feature with the SSIM based feature selection rule. The MRA based method achieves pansharpening without the spatial information of the HS image. The PCA method considers the spatial information with the shadow feature. As for the SCAAE based method, the deep feature is extracted from the network.

Table 1. Average objective results of different methods on four data sets.

Method	CC	SAM	RMSE	ERGAS
Traditional	0.9366	3.9592	0.0295	6.1127
PCA	0.9449	4.9920	0.0331	5.0015
SCAAE	0.9531	3.8884	0.0263	5.0194

lists the average objective results of the traditional MRA based method, PCA based method, and the SCAAE based method on the four tested data sets.

4.4. Pansharpening Results

The first experiment is tested on the Moffett Field data set. Figure 5a–c show the reference high-resolution HS image, the interpolated HS image, and the PAN image, respectively. Figure 5d–n show the false-color results of the estimated HR HS images obtained by different methods and the proposed method. The SFIM method preserves spectral information well, but some of the edges and texture are too sharpened. Results from MTF-based methods are similar to the SFIM method. This may come from the fact that the experiments are performed on simulated data sets, and MTF-based methods may not be fully realizing its potential. The GS-based methods achieve excellent spatial performance but visible spectral distortion. The results generated by GFPCA and CNMF are fuzzy since the effective spatial information is not sufficiently injected. The CNMF method shows promising results in the aspect of spectral, whereas the edges in the reconstructed images obtained by the CNMF method are too sharp in some areas, such as trees in the CNMF fused image. The Fuse and HySure methods show outstanding performance, but some details in the field are injected insufficiently, and the spectral information is not well preserved. The Lanaras’s method produces spectral aberration due to a much higher chromatic aberration in some areas other than the real ground. On the contrary, the proposed method has favorable results. The halo artifacts and the blurring problems can be eliminated by the proposed method.

The objective quantitative analysis for the Moffett Field data set is depicted in

Table 2. Objective performance of eleven methods on the Moffett Field data set.

Method	CC	SAM	RMSE	ERGAS
SFIM	0.8981	7.2029	0.1158	22.9833
MTF_GLP	0.9418	7.6512	0.0399	6.4846
MTF_GLP_HPM	0.9054	7.2158	0.2351	47.3113
GS	0.9086	11.4507	0.0498	8.0635
GSA	0.9595	6.8144	0.0351	5.5188
GFPCA	0.9491	8.0828	0.0381	6.1399
CNMF	0.9767	6.2205	0.0257	4.1122
Lanaras’s	0.9682	9.3145	0.0297	4.8267
HySure	0.9806	5.8031	0.0244	3.9062
Fuse	0.9790	5.6216	0.0249	3.9313
Proposed	0.9807	4.8792	0.0225	3.6749

. After analyzing the experimental data in Table 2, we conclude that the proposed method obtains all the best values in SAM, RMSE, CC, and ERGAS. The results demonstrate that the proposed method performs well in spatial and spectral domains and gains the least global error.

For clearly demonstrating the performance of different pansharpening methods, the difference map is generated by subtracting the reference image from the pansharpened image pixel by pixel. From the results shown in Figure 6, we can see that the difference map obtained by our proposed method has the smallest value difference, which means that the fusion result obtained by this method is closest to the reference image.

The second experiment is conducted on the Salinas Scene data set. Figure 7a–c show the reference high-resolution HS image, the interpolated HS image, and the PAN image, respectively. Figure 7d–n show the false-color results of the estimated HR HS images obtained by different methods and the proposed method. From the visual analysis, we can know that the spatial details in the results of the SFIM method are slightly fuzzy. The GS method causes pronounced spectral distortion and lacks spatial detail information. In comparison, the GFPCA method has better spectral quality than GSA but shows an indistinct area in the left region. Although the Lanaras’s and Fuse methods have a good spatial quality, they generate obvious spectral distortion in the lower half of the scene. It can be seen clearly that the result of HySure suffers from obvious spectral loss, and the details are injected insufficiently. For the Salinas Scene data set, the CNMF and GFPCA methods have high fidelity in rendering the spatial details, but the color difference from the reference image is relatively ignorable, which means spectral distortion. By contrast, the proposed method improves the spatial performance while maintaining spectral information and achieves the superior property in the spatial aspect as it adds more spatial details. The results of the proposed method are closest to the reference image. These facts show that the proposed algorithm performs well in both the spatial and spectral aspects.

The objective quantitative analysis for the Salinas Scene data set is shown in

Table 3. Objective performance of eleven methods on the Salinas Scene data set.

Method	CC	SAM	RMSE	ERGAS
SFIM	0.9161	2.7296	0.0607	6.0684
MTF_GLP	0.9360	2.8550	0.0260	3.4486
MTF_GLP_HPM	0.9042	2.7974	0.0331	14.1318
GS	0.8065	5.0890	0.0498	5.1079
GSA	0.9568	2.2193	0.0191	2.6628
GFPCA	0.9587	2.2229	0.0179	2.6721
CNMF	0.9580	1.9113	0.0159	2.7768
Lanaras’s	0.9558	3.3019	0.0184	2.8786
HySure	0.9170	2.5900	0.0318	3.6303
Fuse	0.9470	2.0426	0.0188	2.9828
Proposed	0.9683	1.3333	0.0106	5.5870

. By analyzing the average values of SAM, CC, RMSE, and ERGAS, we can conclude that the proposed method has the most significant values in CC, the smallest values in SAM and RMSE. Based on the comparison of different methods, the proposed method indeed demonstrates the excellent performance in visual quality and objective indicators.

In addition, as shown in Figure 8, the difference map is calculated to verify the effectiveness of the proposed method further. Similar to the Moffett data set, the blue areas in the difference map of this method are larger than that of other competing methods. In addition, it can be observed that, for all the comparison methods, the major differences in edges and pixels mainly exist on small scales, which can further explore the solution in the future.

The third experiment is performed on the Pavia University data set. Figure 9a–c show the reference high-resolution HS image, the interpolated HS image, and the PAN image, respectively. Figure 9d–n show the false-color results of the estimated HR HS images obtained by different methods and the proposed method for the Pavia University data set. Visually, the results of the SFIM, GS, and GFPCA methods generate spectral distortion. The results of the GSA methods are dim and blurred in some areas such as edges of metal sheets for the lack of sufficient spatial information injection of the PAN image and HS image. By analyzing and comparing the listed results, we can draw the conclusion that the MTF-based methods have good fusion performance, and the GFPCA methods achieve better capability in preserving the spectral information compared with the GS and MTF-based methods. The HySure, FUSE, and CNMF methods keep spectral information very accurate. However, they have a deficient improvement of the spatial quality in some marginal areas, such as the edges of trees and roofs. By contrast, the Lanaras’s and the proposed methods can achieve satisfactory performance, and the false-color image obtained by the proposed method is closest to the reference one.

All the quality measures for each comparison method on the Pavia University dataset have been calculated and recorded. Average results have been shown in

Table 4. Objective performance of eleven methods on the University of Pavia data set.

Method	CC	SAM	RMSE	ERGAS
SFIM	0.8030	9.1332	0.0661	8.4744
MTF_GLP	0.8128	9.7222	0.0654	8.2061
MTF_GLP_HPM	0.8125	9.0571	0.0652	8.2362
GS	0.8380	9.3965	0.0594	7.4222
GSA	0.8767	7.5491	0.0524	5.9046
GFPCA	0.8318	9.0567	0.0638	8.0750
CNMF	0.8942	7.1694	0.0496	6.1852
Lanaras’s	0.9061	6.9648	0.0464	5.4026
HySure	0.9057	6.8168	0.0492	5.5849
Fuse	0.8871	7.5023	0.0550	6.1173
Proposed	0.9125	6.7561	0.0447	5.5199

. For the Pavia University data set, the objective quantitative analysis in Table 4 shows that the proposed method obtains the most significant CC value and the smallest RMSE and SAM values. The ERGAS value reaches the second-best. Generally speaking, the proposed method has a better fusion effect than other algorithms. In particular, the SAM of the proposed method consistently demonstrates the best objective result. This further demonstrates that the proposed method performs well in spatial and spectral aspects.

The absolute difference map between the fused image and the reference image obtained by different methods is shown in Figure 10. It is obvious that the difference map obtained by our proposed method has more blue areas, which means that the difference of pixels obtained by our proposed method is smaller than other compared methods.

Similar to the above three experiments, the fourth test on the Chikusei data set was conducted. Figure 11a–c show the reference high-resolution HS image, the interpolated HS image, and the PAN image, respectively. The fused false-color results obtained by different compared methods and the proposed method are shown in Figure 11d–n. The SFIM method has a significant spectral distortion, and the spatial information of the GS and GSA method is injected insufficiently. Here, the MTF based methods and GS based methods do not perform well in spatial. For the result of the GFPCA method shown in Figure 11h, the spatial details are injected insufficiently, and the fused HS image is fuzzy. By contrast, the HySure, CNMF, and the proposed method can achieve better performance, and the false-color image obtained by the CNMF and the proposed method is closest to the reference one. The Lanaras’s method has a slight spectral distortion in the edges, and the spatial information is added deficiently. Furthermore, it can be observed that the main distortion of generated HR HS images exists in edges and pixels with a small scale for all compared methods. This may be the direction for our future improvement. For overall consideration, the proposed method achieves better performance than the compared ten state-of-the-art methods.

The objective quantitative analysis of the Chikusei data set in

Table 5. Objective performance of eleven methods on the Chikusei data set.

Method	CC	SAM	RMSE	ERGAS
SFIM	0.8785	3.9666	0.0496	6.6972
MTF_GLP	0.8632	4.6774	0.0562	6.7826
MTF_GLP_HPM	0.8737	3.9370	0.0513	7.5214
GS	0.3509	7.5573	0.1081	11.7341
GSA	0.9154	3.6825	0.0462	4.2997
GFPCA	0.9015	4.0849	0.0466	6.0548
CNMF	0.9550	2.911	0.0313	3.3696
Lanaras’s	0.9269	4.4559	0.0453	4.1022
HySure	0.9604	2.6959	0.0305	3.1157
FUSE	0.9115	4.3286	0.0510	4.4439
Proposed	0.9565	2.5951	0.0277	4.4235

shows that the proposed method has the smallest SAM and RMSE values. The CC value achieves the second-best being a little smaller than HySure. The ERGAS value is somewhat high, probably because the details’ injection is a bit excessive to ensure the quality in the spatial domain. However, for the visualization, we can clearly see that the result of the proposed method is better than other methods for a more detailed texture. In general, the proposed algorithm is better than other methods in the comprehensive performance of spatial and spectral information maintenance.

In this case, the absolute difference map between the fusion results obtained by different methods, and the reference methods are shown in Figure 12. The difference between the difference map obtained by other competing methods and the difference map obtained by the proposed method is quite large, which indicates that the proposed method has a better performance than other methods.

In a word, the proposed method performs well in the objective indicators and visual effects of the above four data sets. This further proves that this method can achieve advanced fusion performance.

5. Discussion

According to the four image quality metrics in Table 2, Table 3, Table 4 and Table 5 for different types of data sets of ten state-of-the-art methods, the proposed SCAAE based pansharpening method is substantiated to better keep the spectral characteristics compared to the other ten competing methods. It can be clarified that Figure 6, Figure 8, Figure 10, and Figure 12 illustrated the spectral reflectance difference vectors of the different methods at four randomly selected locations. The superiority of the proposed method is owing to the employment of the deep features extracted by SCAAE. The extracted features can consider the spatial information not only from the PAN image but also from the HS image, making the spatial information more comprehensive, which improves the spatial quality of the fused image. A simple yet useful feature selection rule based on calculating the SSIM is a practical approach to select the feature that is closest to the PAN map, which plays an essential role in reducing the spectral distortion. While the discussed convincing experiments and analysis have verified the effectiveness of the proposed SCAAE based pansharpening method, there are still some interesting details that can be further discussed as follows and become the future work:

• As a convenient and straightforward unsupervised learning model, the network structure of SCAAE can be improved in spatial information enhancement and spectral information maintenance. Next, we will try to extract richer features using the new loss function.
• As an image quality enhancement method, super-resolution plays a vital role in the preprocessing of each image application field. Next, we will explore more targeted pansharpening methods suitable for specific tasks.
• The optimization equation to solve the proportion of HS and PAN images in the final fusion framework makes it adaptive the find the portion of the HS and PAN image. In future work, we can try to improve our model by adding more priors.

6. Conclusions

In this paper, we propose a new HS pansharpening algorithm based on SCAAE to improve the spatial resolution of LR HS images with HR PAN images. An adaptive fusion approach is proposed to incorporate the deep spatial information of the HS images with PAN images as well as preserve spectral information well. Firstly, we propose SCAAE based pansharpening method to obtain spatial information of the HS image, taking advantage of effective features extracted from the training HS data. Secondly, an adaptive fusion approach with a simple feature selection rule is induced to make full use of the sufficient spatial information of the HS image and PAN image. Finally, to improve the quality of spectral information preservation, we introduce the spatial information from two different sensors into an optimization equation to obtain the fusion proportion of the two parts. Moreover, separate from the modern DNN-based methods for HS pansharpening, we mine deep features of HS image, reduce the computational burden, and obtain comprehensive spatial information. The main advantage of our work is that the deep features extracted through SCAAE provide ignorable spatial information, which plays an essential effect on the final results. As the experimental data shows, through our proposed method, especially the part of the feature extraction and feature selection, the CC, SAM, and RMSE values are improved by about 1.42%, 13.12%, and 29.26%, respectively on average compared to the second best method HySure. Besides, the improvement of the CC, SAM, and RMSE are 17.63%, 0.83%, and 11.02%, respectively better than the MRA based method and 0.87%, 22.11%, 20.66% than the PCA based method, which convincingly demonstrates the validity of spatial information preservation. In general, the proposed method has systematically verified the superiority of the proposed method in the enhancement of spatial information and the preservation of spectral information and proved to be active and well-performed in the results of pansharpening, both theoretically and objectively.