Precise Orbit Determination of BDS-2 and BDS-3 Using SLR
Abstract
:1. Introduction
2. Methodology
2.1. Orbit Determination Strategy
2.2. Orbit Accuracy Assessment
3. Processed Data and SLR Validation
3.1. SLR NPs Data of BDS Satellites
3.2. SLR Validation
4. Results
4.1. The Success Rate of Multi-day Solutions
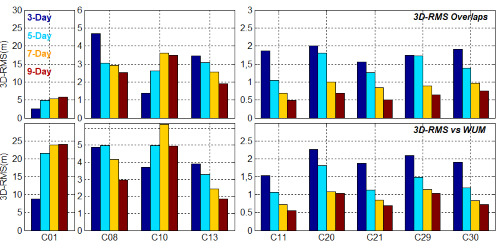
4.2. The Orbit Overlaps and Comparison with WUM Orbits
4.3. The Overall Average 3D-RMS
4.4. The Median RMS of 9-day Solutions
5. Discussion
5.1. The Dependency on the Number of SLR Observations
5.2. The Dependency on the Number of SLR Sites
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Xu, Y.; Li, J.; Yang, C. Progress and performance evaluation of BeiDou global navigation satellite system: Data analysis based on BDS-3 demonstration system. Sci. China Earth Sci. 2018, 61, 614–624. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navigation 2019, 66. [Google Scholar] [CrossRef]
- Degnan, J.J.; Pavlis, E.C. Laser Ranging to GPS Satellites with Centimeter Accuracy. GPS World 1994, 1994, 62–70. [Google Scholar]
- Pavlis, E.C. Comparison of GPS S/C orbits determined from GPS and SLR tracking data. Adv. Space Res. 1995, 16, 55–58. [Google Scholar] [CrossRef]
- Schutz, B.E. Synergism of SLR and GPS. In Proceedings of the Satellite Laser Ranging in the 1990s: Report of the 1994 Belmont Workshop, Elkridge, MD, USA, 1–2 February 1994. [Google Scholar]
- Zhu, S.Y.; Reigber, C.; Kang, Z. Apropos laser tracking to GPS satellites. J. Geod. 1997, 71, 423–431. [Google Scholar] [CrossRef]
- Eanes, R.J.; Nerem, R.S.; Abusali, P.A.M.; Bamford, W.; Ries, J.C. GLONASS Orbit Determination at the Center for Space Research; University of Texas at Austin: Austin, TX, USA, 1999. [Google Scholar]
- Melachroinos, S.A.; Perosanz, F.; Deleflie, F.; Biancalel, R.; Laurain, O.; Exertier, P. GIOVE-A and GPS-35/36 orbit determination and analysis of dynamical properties based on SLR-only tracking data. In Proceedings of the 15th International Workshop on Laser Ranging, Canberra, Australia, 15–20 October 2006. [Google Scholar]
- Schonemann, E.; Springer, T.; Otten, M.; Becker, M.; Dow, J. GIOVE-A precise orbit determination from microwave and satellite laser ranging data—first perspectives for the Galileo constellation and its scientific use. In Proceedings of the First Colloquium on Scientific and Fundamental Aspects of the Galileo Programme, Toulouse, France, 1–4 October 2007; Available online: http://ilrs.gsfc.nasa.gov/docs/2007_Schoenemann_Toulouse_paper.pdf (accessed on 19 October 2019).
- Urschl, C.; Beutler, G.; Gurtner, W.; Hugentober, U.; Ploner, M. Orbit determination for GIOVE-A using SLR tracking data. In Proceedings of the 15th International Workshop on Laser Ranging, Canberra, Australia, 15–20 October 2006; pp. 40–46. [Google Scholar]
- Flohrer, C. Mutual Validation of Satellite-Geodetic Techniques and its Impact on GNSS Orbit Modeling; Geodätisch-geophysikalische Arbeiten in der Schweiz; Swiss Geodetic Commission: Zürich, Switzerland, 2008; Volume 75, ISBN 978-3-908440-19-2. [Google Scholar]
- Zhao, G.; Zhou, S.S.; Zhou, X.H.; Wu, B. Precise Orbit Determination of BeiDou Satellites Using Satellite Laser Ranging; Springer: Berlin/Heidelberg, Germany, 2013; pp. 221–229. [Google Scholar]
- Zhao, G.; Zhou, S.S.; Zhou, X.H.; Wu, B. Comparison on orbit precisions of different types of navigation satellites based on SLR tracking data. In Proceedings of the 18th International Workshop on Laser Ranging, Goar, Germany, 1–3 June 2013. [Google Scholar]
- Bury, G.; Sośnica, K.; Zajdel, R. How many SLR observations and how many stations are needed for deriving high-quality multi-GNSS orbits? In Proceedings of the 2017 ILRS Technical Workshop, Riga, Latvia, 2–5 October 2017. [Google Scholar]
- Bury, G.; Sośnica, K.; Zajdel, R. Multi-GNSS orbit determination using satellite laser ranging. J. Geod. 2019, 1–17. [Google Scholar] [CrossRef]
- Beutler, G.; Brockmann, E.; Gurtner, W. Extended orbit modeling techniques at the CODE processing center of the International GPS Service for geodynamics (IGS): Theory and initial results. Manuscr. Geod. 1994, 19, 367–386. [Google Scholar]
- Standish, E.M., Jr. The observational basis for JPL’s DE 200, the planetary ephemerides of the Astronomical Almanac. Astron. Astrophys. 1990, 233, 252–271. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions. (IERS Technical Note; No. 36) Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie; IERS Technical Note: Frankfurt, Germany, 2010; p. 179. [Google Scholar]
- Mendes, V.B.; Pavlis, E.C. High-accuracy zenith delay prediction at optical wavelengths. Geophys. Res. Lett. 2004, 31, 189–207. [Google Scholar] [CrossRef]
- Yang, H.; Xu, T.; Nie, W.; Gao, F.; Guan, M. SLR validation and evaluation on BDS precise orbits from 2013 to 2018. Adv. Space Res. 2019, 64, 475–490. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software Version 5.2; University of Bern, Bern Open Publishing: Bern, Switzerland, 2015. [Google Scholar]
- Beutler, G.; Brockmann, E.; Hugentobler, U.; Mervart, L.; Rothacher, M.; Weber, R. Combining consecutive short arcs into long arcs for precise and efficient GPS Orbit Determination. J. Geod. 1996, 70, 287–299. [Google Scholar] [CrossRef]
- Lutz, S.; Meindl, M.; Steigenberger, P.; Beutler, G.; Sośnica, K.; Schaer, S.; Dach, R.; Arnold, D.; Thaller, D.; Jäggi, A. Impact of the arc length on GNSS analysis results. J. Geod. 2016, 90, 365–378. [Google Scholar] [CrossRef]
- Prange, L.; Orliac, E.; Dach, R.; Arnold, D.; Beutler, G.; Schaer, S.; Jäggi, A. CODE’s five-system orbit and clock solution—The challenges of multi-GNSS data analysis. J. Geod. 2017, 91, 1–16. [Google Scholar] [CrossRef]
- Urschl, C.; Gurtner, W.; Hugentobler, U.; Schaer, S.; Beutler, G. Validation of GNSS orbits using SLR observations. Adv. Space Res. 2005, 36, 412–417. [Google Scholar] [CrossRef]
- Urschl, C.; Beutler, G.; Gurtner, W.; Hugentobler, U.; Schaer, S. Contribution of SLR tracking data to GNSS orbit determination. Adv. Space Res. 2007, 39, 1515–1523. [Google Scholar] [CrossRef]
- Sośnica, K.; Thaller, D.; Dach, R.; Steigenberger, P.; Beutler, G.; Arnold, D.; Jäggi, A. Satellite laser ranging to GPS and GLONASS. J Geod. 2015, 89, 725–743. [Google Scholar] [CrossRef]
- Yang, H.; Xu, T.; Sun, D. Validation of GPS36 Satellite CODE Precise Orbit with SLR Measurements; China Satellite Navigation Conference (CSNC) 2016 Proceedings: Volume III, Lecture Notes in Electrical Engineering 390; Springer: Singapore, 2016. [Google Scholar] [CrossRef]
- Sośnica, K.; Prange, L.; Kaźmierski, K.; Bury, G.; Drożdżewski, M.; Zajdel, R.; Hadas, T. Validation of Galileo orbits using SLR with a focus on satellites launched into incorrect orbital planes. J. Geod. 2018, 92, 131–148. [Google Scholar] [CrossRef]
- Zajdel, R.; Sośnica, K.; Bury, G. A New Online Service for the Validation of Multi-GNSS Orbits Using SLR. Remote Sens. 2017, 9, 1049. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, C.; Guo, J.; Wang, B.; Liu, J. Precise orbit and clock determination for BeiDou-3 experimental satellites with yaw attitude analysis. GPS Solut. 2017, 22, 4. [Google Scholar] [CrossRef]
- Wang, C.; Guo, J.; Zhao, Q.; Liu, J. Yaw attitude modeling for BeiDou I06 and BeiDou-3 satellites. GPS Solut. 2018, 22, 117. [Google Scholar] [CrossRef]

















| Dynamic Models | Description for BDS SLR |
| Earth Gravity Field | EGM2008 |
| N-body Perturbation | JPL DE405 |
| Solar Radiation Pressure | ECOM |
| Tides and Relativistic | IERS2010 |
| Measurement Models | |
| Basic Observations | SLR NPs |
| A priori Orbital Parameters | Precise orbit of WUM |
| A priori Station Coordinates | SLRF2014 |
| A Priori Troposphere Model | Mendes–Pavlis model |
| Centre-of-Mass Correction of LRAs | ILRS, CAST and SECM |
| Estimated Parameters | |
| Station Coordinates | Strong constrained |
| Orbital Parameters | 6 Orbital Element and 9 ECOM SRP |
| Pseudo-Random Pulse | None |
| ERP | Fixed ERP of WUM |
| Geocentre Coordinates | None |
| Range Bias | All |
| C20/C21 (m) | C29/C30 (m) | |
|---|---|---|
| X | 0.6120 | 0.6646 |
| Y | −0.072 | 0.4249 |
| Z | 1.2230 | 0.6427 |
| PRN | Perc. | Num. | Overall | Noneclip. | Eclip. | NYS | YM |
|---|---|---|---|---|---|---|---|
| C01 | 99.6% | 237 | −7.5/19.0 | −4.2/17.6 | −12.8/21.1 | --/-- | --/-- |
| C08 | 96.6% | 593 | −4.2/7.3 | −4.2/6.9 | −5.7/11.8 | −0.8/3.0 | −16.8/20.8 |
| C10 | 95.5% | 554 | −3.3/6.6 | −3.8/6/0 | −0.5/9.2 | −1.0/8.2 | 0.1/10.1 |
| C13 | 97.9% | 972 | −1.8/5.2 | −1.6/5.1 | −3.2/6.0 | −1.7/4.6 | −4.8/7.3 |
| C11 | 97.8% | 1712 | 0.9/3.4 | 1.1/3.4 | 0.4/3.2 | 0.9/3.1 | −1.7/3.8 |
| C20 | 98.1% | 808 | 0.3/4.6 | 0.3/4.5 | 0.2/5.0 | 0.3/4.7 | 0.2/5.7 |
| C21 | 98.8% | 1037 | 0.0/4.4 | 0.1/4.2 | −0.6/5.4 | −1.3/5.6 | 0.9/5.0 |
| C29 | 97.6% | 922 | −0.4/5.7 | −0.5/5.9 | −0.1/4.8 | 0.9/5.0 | −2.2/4.3 |
| C30 | 99.1% | 889 | −1.4/5.0 | −1.5/5.0 | −1.0/4.8 | −0.9/4.7 | −1.2/5.3 |
| PRN | Overlaps | Vs WUM | ||||||
|---|---|---|---|---|---|---|---|---|
| 3-Day | 5-Day | 7-Day | 9-Day | 3-Day | 5-Day | 7-Day | 9-Day | |
| C01 | 19.8% | 22.1% | 29.1% | 37.2% | 12.7% | 8.7% | 5.8% | 8.1% |
| C08 | 9.3% | 22.1% | 52.3% | 62.2% | 9.8% | 22.5% | 45.1% | 55.5% |
| C10 | 7.0% | 11.0% | 27.3% | 45.3% | 5.8% | 9.8% | 30.1% | 46.2% |
| C13 | 12.2% | 44.2% | 75.6% | 89.0% | 15.6% | 50.3% | 76.3% | 85.5% |
| C11 | 43.0% | 77.9% | 93.0% | 99.4% | 53.2% | 82.1% | 95.4% | 100% |
| C20 | 11.6% | 43.0% | 54.7% | 58.7% | 15.0% | 41.6% | 50.9% | 56.1% |
| C21 | 27.9% | 60.5% | 76.2% | 80.8% | 36.4% | 57.8% | 70.5% | 71.7% |
| C29 | 23.8% | 52.9% | 75.6% | 82.0% | 28.9% | 54.3% | 73.4% | 76.3% |
| C30 | 20.9% | 51.7% | 65.1% | 72.1% | 22.5% | 45.7% | 59.5% | 63.6% |
| 3D-RMS (Min/Max) | 3-Day | 5-Day | 7-Day | 9-Day | |
|---|---|---|---|---|---|
| GEO | 2.61 | 4.80 | 5.28 | 5.77 | |
| Overlaps | IGSO | 1.38/4.70 | 2.61/3.07 | 2.56/3.60 | 1.89/3.49 |
| MEO | 1.55/2.00 | 1.05/1.80 | 0.69/0.99 | 0.49/0.75 | |
| GEO | 8.75 | 21.57 | 23.88 | 23.95 | |
| Vs WUM | IGSO | 3.71/4.89 | 3.28/4.97 | 2.42/6.21 | 1.85/4.95 |
| MEO | 1.54/2.26 | 1.07/1.81 | 0.73/1.14 | 0.55/1.04 | |
| PRN | Overlaps | Vs WUM | ||||||
|---|---|---|---|---|---|---|---|---|
| R | T | N | 3D-RMS | R | T | N | 3D-RMS | |
| C01 | 6.5 | 90.3 | 8.1 | 100.6 | 176.7 | 1796.1 | 367.5 | 2641.8 |
| C08 | 15.4 | 135.3 | 111.3 | 185.8 | 19.0 | 133.5 | 116.8 | 207.5 |
| C10 | 25.0 | 101.9 | 185.1 | 266.0 | 30.7 | 175.9 | 311.5 | 431.4 |
| C13 | 16.9 | 58.4 | 78.0 | 114.4 | 21.6 | 82.1 | 81.1 | 130.1 |
| C11 | 3.6 | 12.4 | 15.6 | 21.4 | 5.7 | 15.0 | 16.5 | 25.7 |
| C20 | 5.7 | 21.6 | 23.4 | 33.3 | 9.0 | 27.2 | 27.2 | 45.8 |
| C21 | 4.9 | 13.6 | 17.6 | 26.1 | 7.3 | 20.4 | 20.6 | 31.0 |
| C29 | 4.8 | 17.5 | 20.7 | 31.4 | 9.6 | 36.8 | 35.2 | 57.9 |
| C30 | 4.8 | 15.6 | 23.9 | 32.3 | 6.0 | 22.3 | 30.1 | 41.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Xu, T.; Nie, W.; Gao, F.; Guan, M. Precise Orbit Determination of BDS-2 and BDS-3 Using SLR. Remote Sens. 2019, 11, 2735. https://doi.org/10.3390/rs11232735
Yang H, Xu T, Nie W, Gao F, Guan M. Precise Orbit Determination of BDS-2 and BDS-3 Using SLR. Remote Sensing. 2019; 11(23):2735. https://doi.org/10.3390/rs11232735
Chicago/Turabian StyleYang, Honglei, Tianhe Xu, Wenfeng Nie, Fan Gao, and Meiqian Guan. 2019. "Precise Orbit Determination of BDS-2 and BDS-3 Using SLR" Remote Sensing 11, no. 23: 2735. https://doi.org/10.3390/rs11232735
APA StyleYang, H., Xu, T., Nie, W., Gao, F., & Guan, M. (2019). Precise Orbit Determination of BDS-2 and BDS-3 Using SLR. Remote Sensing, 11(23), 2735. https://doi.org/10.3390/rs11232735