Use of A Neural Network-Based Ocean Body Radiative Transfer Model for Aerosol Retrievals from Multi-Angle Polarimetric Measurements
Abstract
:1. Introduction
2. Retrieval Method
2.1. Forward Model
2.1.1. Atmosphere Model
2.1.2. Ocean Model
2.2. Inversion Methodology
3. Neural Network Design
3.1. Training Set Generation
3.2. Neural Network Training
4. Data
4.1. SPEX Airborne Data
4.2. HSRL-2 Data
4.3. Aeronet Data
4.4. Re-Analysis Data
5. Synthetic Retrieval
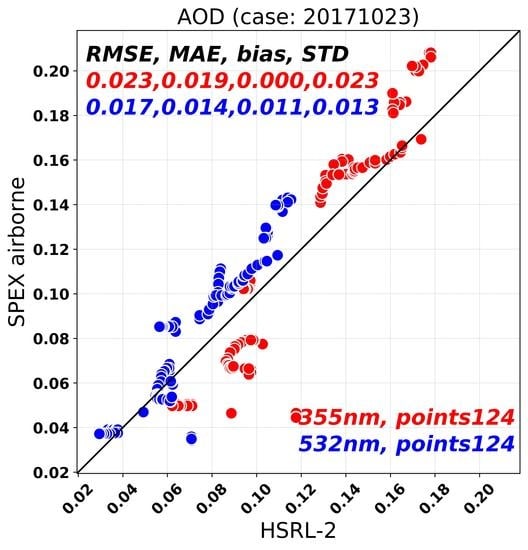
6. Retrievals from SPEX Airborne during ACEPOL
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Loeb, N.G.; Su, W.Y. Direct Aerosol Radiative Forcing Uncertainty Based on a Radiative Perturbation Analysis. J. Clim. 2010, 23, 5288–5293. [Google Scholar] [CrossRef]
- Johnson, B.T.; Shine, K.P.; Forster, P.M. The semi-direct aerosol effect: Impact of absorbing aerosols on marine stratocumulus. Q. J. R. Meteorol. Soc. 2004, 130, 1407–1422. [Google Scholar] [CrossRef] [Green Version]
- Lohmann, U.; Feichter, J. Global indirect aerosol effects: A review. Atmos. Chem. Phys. 2005, 5, 715–737. [Google Scholar] [CrossRef] [Green Version]
- Albrecht, B.A. Aerosols, cloud microphysics, and fractional cloudiness. Science 1989, 245, 1227–1230. [Google Scholar] [CrossRef]
- Ramanathan, V.; Crutzen, P.J.; Kiehl, J.T.; Rosenfeld, D. Atmosphere—Aerosols, climate, and the hydrological cycle. Science 2001, 294, 2119–2124. [Google Scholar] [CrossRef] [Green Version]
- Rosenfeld, D.; Lohmann, U.; Raga, G.B.; O’Dowd, C.D.; Kulmala, M.; Fuzzi, S.; Reissell, A.; Andreae, M.O. Flood or drought: How do aerosols affect precipitation? Science 2008, 321, 1309–1313. [Google Scholar] [CrossRef] [Green Version]
- Pachauri, R.; Meyer, L.; Plattner, G.; Stocker, T. IPCC, 2014: Climate Change 2014: Synthesis Report; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Hasekamp, O.P.; Gryspeerdt, E.; Quaas, J. Analysis of polarimetric satellite measurements suggests stronger cooling due to aerosol-cloud interactions. Nat. Commun. 2019, 5405. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Cairns, B.; Hansen, J.E.; Travis, L.D.; Burg, R.; Kaufman, Y.J.; Vanderlei Martins, J.; Shettle, E.P. Monitoring of aerosol forcing of climate from space: Analysis of measurement requirements. J. Quant. Spectrosc. Radiat. Transf. 2004, 88, 149–161. [Google Scholar] [CrossRef]
- Dubovik, O.; Herman, M.; Holdak, A.; Lapyonok, T.; Tanre, D.; Deuze, J.L.; Ducos, F.; Sinyuk, A.; Lopatin, A. Statistically optimized inversion algorithm for enhanced retrieval of aerosol properties from spectral multi-angle polarimetric satellite observations. Atmos. Meas. Tech. 2011, 4, 975–1018. [Google Scholar] [CrossRef] [Green Version]
- Hasekamp, O.P.; Litvinov, P.; Butz, A. Aerosol properties over the ocean from PARASOL multiangle photopolarimetric measurements. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Levy, R.C.; Mattoo, S.; Munchak, L.A.; Remer, L.A.; Sayer, A.M.; Patadia, F.; Hsu, N.C. The Collection 6 MODIS aerosol products over land and ocean. Atmos. Meas. Tech. 2013, 6, 2989–3034. [Google Scholar] [CrossRef] [Green Version]
- Hsu, N.C.; Jeong, M.J.; Bettenhausen, C.; Sayer, A.M.; Hansell, R.; Seftor, C.S.; Huang, J.; Tsay, S.C. Enhanced Deep Blue aerosol retrieval algorithm: The second generation. J. Geophys. Res. Atmos. 2013, 118, 9296–9315. [Google Scholar] [CrossRef]
- Sayer, A.M.; Hsu, N.C.; Bettenhausen, C.; Jeong, M.J.; Meister, G. Effect of MODIS Terra radiometric calibration improvements on Collection 6 Deep Blue aerosol products: Validation and Terra/Aqua consistency. J. Geophys. Res. Atmos. 2015, 120. [Google Scholar] [CrossRef] [Green Version]
- Diner, D.J.; Beckert, J.C.; Reilly, T.H.; Bruegge, C.J.; Conel, J.E.; Kahn, R.A.; Martonchik, J.V.; Ackerman, T.P.; Davies, R.; Gerstl, S.A.W.; et al. Multi-angle Imaging SpectroRadiometer (MISR)—Instrument description and experiment overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1072–1087. [Google Scholar] [CrossRef]
- Limbacher, J.A.; Kahn, R.A. Updated MISR over-water research aerosol retrieval algorithm—Part 2: A multi-angle aerosol retrieval algorithm for shallow, turbid, oligotrophic, and eutrophic waters. Atmos. Meas. Tech. 2019, 12, 675–689. [Google Scholar] [CrossRef] [Green Version]
- De Leeuw, G.; Holzer-Popp, T.; Bevan, S.; Davies, W.H.; Descloitres, J.; Grainger, R.G.; Griesfeller, J.; Heckel, A.; Kinne, S.; Kluser, L.; et al. Evaluation of seven European aerosol optical depth retrieval algorithms for climate analysis. Remote Sens. Environ. 2015, 162, 295–315. [Google Scholar] [CrossRef] [Green Version]
- Popp, T.; De Leeuw, G.; Bingen, C.; Bruhl, C.; Capelle, V.; Chedin, A.; Clarisse, L.; Dubovik, O.; Grainger, R.; Griesfeller, J.; et al. Development, Production and Evaluation of Aerosol Climate Data Records from European Satellite Observations (Aerosol_cci). Remote Sens. 2016, 8, 421. [Google Scholar] [CrossRef] [Green Version]
- Kahn, R.A.; Gaitley, B.J. An analysis of global aerosol type as retrieved by MISR. J. Geophys. Res. Atmos. 2015, 120, 4248–4281. [Google Scholar] [CrossRef]
- Deschamps, P.Y.; Breon, F.M.; Leroy, M.; Podaire, A.; Bricaud, A.; Buriez, J.C.; Seze, G. The polder mission: Instrument characteristics and scientific objectives. IEEE Trans. Geosci. Remote Sens. 1994, 32, 598–615. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.; Liu, Y.; Xu, X.G.; Cai, Z.N.; Yang, D.X.; Yan, C.X.; Feng, L. Angular dependence of aerosol information content in CAPI/TanSat observation over land: Effect of polarization and synergy with A-train satellites. Remote Sens. Environ. 2017, 196, 163–177. [Google Scholar] [CrossRef]
- Li, Z.Q.; Hou, W.Z.; Hong, J.; Zheng, F.X.; Luo, D.G.; Wang, J.; Gu, X.F.; Qiao, Y.L. Directional Polarimetric Camera (DPC): Monitoring aerosol spectral optical properties over land from satellite observation. J. Quant. Spectrosc. Radiat. Transf. 2018, 218, 21–37. [Google Scholar] [CrossRef]
- Fougnie, B.; Marbach, T.; Lacan, A.; Lang, R.; Schlussel, P.; Poli, G.; Munro, R.; Couto, A.B. The multi-viewing multi-channel multi-polarisation imager—Overview of the 3MI polarimetric mission for aerosol and cloud characterization. J. Quant. Spectrosc. Radiat. Transf. 2018, 219, 23–32. [Google Scholar] [CrossRef]
- Hasekamp, O.P.; Fu, G.L.; Rusli, S.P.; Wu, L.H.; Di Noia, A.; De Brugh, J.A.; Landgraf, J.; Smit, J.M.; Rietjens, J.; Van Amerongen, A. Aerosol measurements by SPEXone on the NASA PACE mission: Expected retrieval capabilities. J. Quant. Spectrosc. Radiat. Transf. 2019, 227, 170–184. [Google Scholar] [CrossRef]
- Van Amerongen, A.; Rietjens, J.; Campo, J.; Dogan, E.; Dingjan, J.; Nalla, R.; Caron, J.; Hasekamp, O. SPEXone: A compact multi-angle polarimeter. In Proceedings of the International Conference on Space Optics—ICSO 2018, Chania, Greece, 9–12 October 2018. [Google Scholar] [CrossRef] [Green Version]
- Rietjens, J.; Campo, J.; Chanumolu, A.; Smit, M.; Nalla, R.; Fernandez, C.; Dingjan, J.; Amerongen, A.; Hasekamp, O. Expected Performance and Error Analysis for Spexone, a Multi-Angle Channeled Spectropolarimeter for the NASA PACE Mission. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 11–15 August 2019; p. 8. [Google Scholar] [CrossRef]
- Martins, J.V.; Fernandez-Borda, R.; McBride, B.; Remer, L.; Barbosa, H.M.J.; IEEE. The Harp Hyperangular Imaging Polarimeter And The Need For Small Satellite Payloads With High Science Payoff For Earth Science Remote Sensing. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2018), Valencia, Spain, 22–27 July 2018; pp. 6304–6307. [Google Scholar]
- Diner, D.J.; Boland, S.W.; Brauer, M.; Bruegge, C.; Burke, K.A.; Chipman, R.; Di Girolamo, L.; Garay, M.J.; Hasheminassab, S.; Hyer, E.; et al. Advances in multiangle satellite remote sensing of speciated airborne particulate matter and association with adverse health effects: From MISR to MAIA. J. Appl. Remote Sens. 2018, 12. [Google Scholar] [CrossRef] [Green Version]
- Mishchenko, M.I.; Travis, L.D. Satellite retrieval of aerosol properties over the ocean using polarization as well as intensity of reflected sunlight. J. Geophys. Res. Atmos. 1997, 102, 16989–17013. [Google Scholar] [CrossRef] [Green Version]
- Chowdhary, J.; Cairns, B.; Mishchenko, M.; Travis, L. Retrieval of aerosol properties over the ocean using multispectral and multiangle photopolarimetric measurements from the Research Scanning Polarimeter. Geophys. Res. Lett. 2001, 28, 243–246. [Google Scholar] [CrossRef]
- Dubovik, O.; Li, Z.; Mishchenko, M.I.; Tanré, D.; Karol, Y.; Bojkov, B.; Cairns, B.; Diner, D.J.; Espinosa, W.R.; Goloub, P.; et al. Polarimetric remote sensing of atmospheric aerosols: Instruments, methodologies, results, and perspectives. J. Quant. Spectrosc. Radiat. Transf. 2019, 224, 474–511. [Google Scholar] [CrossRef]
- Hasekamp, O.P.; Landgraf, J. Retrieval of aerosol properties over land surfaces: Capabilities of multiple-viewing-angle intensity and polarization measurements. Appl. Opt. 2007, 46, 3332–3344. [Google Scholar] [CrossRef]
- Hou, W.; Li, Z.; Wang, J.; Xu, X.; Goloub, P.; Qie, L. Improving Remote Sensing of Aerosol Microphysical Properties by Near-Infrared Polarimetric Measurements Over Vegetated Land: Information Content Analysis. J. Geophys. Res. Atmos. 2018, 123, 2215–2243. [Google Scholar] [CrossRef]
- Xu, F.; Dubovik, O.; Zhai, P.W.; Diner, D.J.; Kalashnikova, O.V.; Seidel, F.C.; Litvinov, P.; Bovchaliuk, A.; Garay, M.J.; Van Harten, G.; et al. Joint retrieval of aerosol and water-leaving radiance from multispectral, multiangular and polarimetric measurements over ocean. Atmos. Meas. Tech. 2016, 9, 2877–2907. [Google Scholar] [CrossRef] [Green Version]
- Gao, M.; Zhai, P.W.; Franz, B.; Hu, Y.X.; Knobelspiesse, K.; Werdell, P.J.; Ibrahim, A.; Xu, F.; Cairns, B. Retrieval of aerosol properties and water-leaving reflectance from multi-angular polarimetric measurements over coastal waters. Opt. Express 2018, 26, 8968–8989. [Google Scholar] [CrossRef] [PubMed]
- Zhai, P.W.; Boss, E.; Franz, B.; Werdell, P.J.; Hu, Y.X. Radiative Transfer Modeling of Phytoplankton Fluorescence Quenching Processes. Remote Sens. 2018, 10, 1309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stamnes, S.; Hostetler, C.; Ferrare, R.; Burton, S.; Liu, X.; Hair, J.; Hu, Y.; Wasilewski, A.; Martin, W.; van Diedenhoven, B.; et al. Simultaneous polarimeter retrievals of microphysical aerosol and ocean color parameters from the “MAPP” algorithm with comparison to high-spectral-resolution lidar aerosol and ocean products. Appl. Opt. 2018, 57, 2394–2413. [Google Scholar] [CrossRef] [PubMed]
- Diner, D.J.; Garay, M.J.; Kalashnikova, O.V.; Rheingans, B.E.; Geier, S.; Bull, M.A.; Jovanovic, V.M.; Xu, F.; Bruegge, C.J.; Davis, A.; et al. Airborne Multiangle SpectroPolarimetric Imager (AirMSPI) observations over California during NASA’s Polarimeter Definition Experiment (PODEX). In Proceedings of the Conference on Polarization Science and Remote Sensing VI, San Diego, CA, USA, 26–29 August 2013. [Google Scholar]
- Zhai, P.W.; Knobelspiesse, K.; Ibrahim, A.; Franz, B.A.; Hu, Y.X.; Gao, M.; Frouin, R. Water-leaving contribution to polarized radiation field over ocean. Opt. Express 2017, 25, 689–708. [Google Scholar] [CrossRef] [PubMed]
- Werdell, P.J.; McKinna, L.I.W. Sensitivity of Inherent Optical Properties From Ocean Reflectance Inversion Models to Satellite Instrument Wavelength Suites. Front. Earth Sci. 2019, 7, 54. [Google Scholar] [CrossRef]
- Werbos, P.J. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
- Leshno, M.; Lin, V.Y.; Pinkus, A.; Schocken, S. Multilayer Feedforward Networks With A Nonpolynomial Activation Function Can Approximate Any Function. Neural Netw. 1993, 6, 861–867. [Google Scholar] [CrossRef] [Green Version]
- Chevallier, F.; Cheruy, F.; Scott, N.A.; Chedin, A. A neural network approach for a fast and accurate computation of a longwave radiative budget. J. Appl. Meteorol. 1998, 37, 1385–1397. [Google Scholar] [CrossRef]
- Chevallier, F.; Morcrette, J.J.; Cheruy, F.; Scott, N.A. Use of a neural-network-based long-wave radiative-transfer scheme in the ECMWF atmospheric model. Q. J. R. Meteorol. Soc. 2000, 126, 761–776. [Google Scholar] [CrossRef]
- Cornford, D.; Nabney, I.T.; Ramage, G. Improved neural network scatterometer forward models. J. Geophys. Res. Oceans 2001, 106, 22331–22338. [Google Scholar] [CrossRef] [Green Version]
- Krasnopolsky, V.M. Neural network emulations for complex multidimensional geophysical mappings: Applications of neural network techniques to atmospheric and oceanic satellite retrievals and numerical modeling. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
- Stamnes, S.; Fang, Y.Z.; Chen, N.; Lie, W.; Tanikawa, T.; Lin, Z.Y.; Liu, X.; Burton, S.; Omar, A.; Stamnes, J.J.; et al. Advantages of Measuring the Q Stokes Parameter in Addition to the Total Radiance/in the Detection of Absorbing Aerosols. Front. Earth Sci. 2018, 6, 34. [Google Scholar] [CrossRef]
- Bue, B.D.; Thompson, D.R.; Deshpande, S.; Eastwood, M.; Green, R.O.; Natraj, V.; Mullen, T.; Parente, M. Neural network radiative transfer for imaging spectroscopy. Atmos. Meas. Tech. 2019, 12, 2567–2578. [Google Scholar] [CrossRef] [Green Version]
- Nanda, S.; Graaf, M.; Veefkind, J.; Linden, M.; Sneep, M.; Haan, J.; Levelt, P. A neural network radiative transfer model approach applied to TROPOMI’s aerosol height algorithm. Atmos. Meas. Tech. Discuss. 2019. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995; Volume 12, pp. 1235–1242. [Google Scholar]
- Aires, F.; Rossow, W.B. Inferring instantaneous, multivariate and nonlinear sensitivities for the analysis of feedback processes in a dynamical system: Lorenz model case-study. Q. J. R. Meteorol. Soc. 2003, 129, 239–275. [Google Scholar] [CrossRef] [Green Version]
- Blackwell, W.J. Neural network Jacobian analysis for high-resolution profiling of the atmosphere. EURASIP J. Adv. Signal Process. 2012, 2012, 71. [Google Scholar] [CrossRef] [Green Version]
- Jimenez, C.; Eriksson, P. A neural network technique for inversion of atmospheric observations from microwave limb sounders. Radio Sci. 2001, 36, 941–953. [Google Scholar] [CrossRef]
- Dubovik, O.; Sinyuk, A.; Lapyonok, T.; Holben, B.N.; Mishchenko, M.; Yang, P.; Eck, T.F.; Volten, H.; Munoz, O.; Veihelmann, B.; et al. Application of spheroid models to account for aerosol particle nonsphericity in remote sensing of desert dust. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Fu, G.; Hasekamp, O. Retrieval of aerosol microphysical and optical properties over land using a multimode approach. Atmos. Meas. Tech. 2018, 11, 6627–6650. [Google Scholar] [CrossRef] [Green Version]
- D’Almeida, G.A.; Koepke, P.; Shettle, E.P. Atmospheric Aerosols: Global Climatology and Radiative Characteristics; A Deepak Pub: Hampton, VA, USA, 1991; Volume 54, pp. 55–61. [Google Scholar]
- Wu, L.; Hasekamp, O.; Van Diedenhoven, B.; Cairns, B. Aerosol retrieval from multiangle, multispectral photopolarimetric measurements: Importance of spectral range and angular resolution. Atmos. Meas. Tech. 2015, 8, 2625–2638. [Google Scholar] [CrossRef] [Green Version]
- Cox, C. Statistics of the sea surface derived from sun glitter. J. Mar. Res. 1954, 13, 198–227. [Google Scholar]
- Chowdhary, J.; Cairns, B.; Waquet, F.; Knobelspiesse, K.; Ottaviani, M.; Redemann, J.; Travis, L.; Mishchenko, M. Sensitivity of multiangle, multispectral polarimetric remote sensing over open oceans to water-leaving radiance: Analyses of RSP data acquired during the MILAGRO campaign. Remote Sens. Environ. 2012, 118, 284–308. [Google Scholar] [CrossRef]
- Chowdhary, J.; Cairns, B.; Travis, L.D. Contribution of water-leaving radiances to multiangle, multispectral polarimetric observations over the open ocean: Bio-optical model results for case 1 waters. Appl. Opt. 2006, 45, 5542–5567. [Google Scholar] [CrossRef]
- Smith, R.C.; Baker, K.S. Optical-properties of the clearest natural-waters (200–800 nm). Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef]
- Wien, W.; Planck, M. Annalen der Physik; J. Barth: Warendorf, Germany, 1908; Volume 27. [Google Scholar]
- Siegel, D.A.; Maritorena, S.; Nelson, N.B.; Hansell, D.A.; Lorenzi-Kayser, M. Global distribution and dynamics of colored dissolved and detrital organic materials. J. Geophys. Res. Oceans 2002, 107. [Google Scholar] [CrossRef]
- Landgraf, J.; Hasekamp, O.P.; Box, M.A.; Trautmann, T. A linearized radiative transfer model for ozone profile retrieval using the analytical forward-adjoint perturbation theory approach. J. Geophys. Res. Atmos. 2001, 106, 27291–27305. [Google Scholar] [CrossRef] [Green Version]
- Hasekamp, O.P.; Landgraf, J. A linearized vector radiative transfer model for atmospheric trace gas retrieval. J. Quant. Spectrosc. Radiat. Transf. 2002, 75, 221–238. [Google Scholar] [CrossRef]
- Hasekamp, O.P.; Landgraf, J. Linearization of vector radiative transfer with respect to aerosol properties and its use in satellite remote sensing. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Schepers, D.; De Brugh, J.; Hahne, P.; Butz, A.; Hasekamp, O.P.; Landgraf, J. LINTRAN v2.0: A linearised vector radiative transfer model for efficient simulation of satellite-born nadir-viewing reflection measurements of cloudy atmospheres. J. Quant. Spectrosc. Radiat. Transf. 2014, 149, 347–359. [Google Scholar] [CrossRef]
- Tikhonov, A.N. Solution of incorrectly formulated problems and regularization method. Dokl. Akad. Nauk SSSR 1963, 151, 501–504. [Google Scholar]
- Phillips, D.L. A technique for the numerical solution of certain integral equations of the first kind. JACM 1962, 9, 84–97. [Google Scholar] [CrossRef]
- Hou, W.Z.; Wang, J.; Xu, X.G.; Reid, J.S.; Han, D. An algorithm for hyperspectral remote sensing of aerosols: 1. Development of theoretical framework. J. Quant. Spectrosc. Radiat. Transf. 2016, 178, 400–415. [Google Scholar] [CrossRef]
- Gordon, H.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Di Noia, A.; Hasekamp, O.P.; Van Harten, G.; Rietjens, J.H.H.; Smit, J.M.; Snik, F.; Henzing, J.S.; De Boer, J.; Keller, C.U.; Volten, H. Use of neural networks in ground-based aerosol retrievals from multi-angle spectropolarimetric observations. Atmos. Meas. Tech. 2015, 8, 281–299. [Google Scholar] [CrossRef] [Green Version]
- Di Noia, A.; Sellitto, P.; Del Frate, F.; De Laat, J. Global tropospheric ozone column retrievals from OMI data by means of neural networks. Atmos. Meas. Tech. 2013, 6, 895–915. [Google Scholar] [CrossRef] [Green Version]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations By Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Bös, S.; Amari, S.I. Annealed online learning in multilayer neural networks. In On-Line Learning in Neural Networks; Cambridge University Press: New York, NY, USA, 1998. [Google Scholar]
- Smit, M.; Rietjens, J.; Hasekamp, O.P.; Noia, A.D.; Van Harten, G.; Rheingans, B.E.; Diner, D.J.; Seidel, F.C.; Kalashnikova, O.V. First results of the SPEX airborne multi-angle spectropolarimeter—Aerosol retrievals over ocean and intercomparison with AirMSPI. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 11–15 December 2016. [Google Scholar]
- Rietjens, J.; Smit, M.; Hasekamp, O.P.; Grim, M.; Eggens, M.; Eigenraam, A.; Keizer, G.; Van Loon, D.; Talsma, J.; Van der Vlugt, J.; et al. The SPEX-airborne multi-angle spectropolarimeter on NASA’s ER-2 research aircraft: Capabilities, data processing and data products. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 11–15 December 2016. [Google Scholar]
- Van Harten, G.; De Boer, J.; Rietjens, J.H.H.; Di Noia, A.; Snik, F.; Volten, H.; Smit, J.M.; Hasekamp, O.P.; Henzing, J.S.; Keller, C.U. Atmospheric aerosol characterization with a ground-based SPEX spectropolarimetric instrument. Atmos. Meas. Tech. 2014, 7, 4341–4351. [Google Scholar] [CrossRef] [Green Version]
- Smit, J.M.; Rietjens, J.H.H.; Van Harten, G.; Di Noia, A.; Laauwen, W.; Rheingans, B.E.; Diner, D.J.; Cairns, B.; Wasilewski, A.; Knobelspiesse, K.D.; et al. SPEX airborne spectropolarimeter calibration and performance. Appl. Opt. 2019, 58, 5695–5719. [Google Scholar] [CrossRef]
- Hair, J.W.; Hostetler, C.A.; Cook, A.L.; Harper, D.B.; Ferrare, R.A.; Mack, T.L.; Welch, W.; Izquierdo, L.R.; Hovis, F.E. Airborne High Spectral Resolution Lidar for profiling aerosol optical properties. Appl. Opt. 2008, 47, 6734–6752. [Google Scholar] [CrossRef]
- Burton, S.P.; Ferrare, R.A.; Hostetler, C.A.; Hair, J.W.; Rogers, R.R.; Obland, M.D.; Butler, C.F.; Cook, A.L.; Harper, D.B.; Froyd, K.D. Aerosol classification using airborne High Spectral Resolution Lidar measurements—Methodology and examples. Atmos. Meas. Tech. 2012, 5, 73–98. [Google Scholar] [CrossRef] [Green Version]
- Rogers, R.R.; Hair, J.W.; Hostetler, C.A.; Ferrare, R.A.; Obland, M.D.; Cook, A.L.; Harper, D.B.; Burton, S.P.; Shinozuka, Y.; McNaughton, C.S.; et al. NASA LaRC airborne high spectral resolution lidar aerosol measurements during MILAGRO: Observations and validation. Atmos. Chem. Phys. 2009, 9, 4811–4826. [Google Scholar] [CrossRef] [Green Version]
- Fu, G.; Hasekamp, O.; Rietjens, J.; Smit, M.; Di Noia, A.; Cairns, B.; Wasilewski, A.; Diner, D.; Xu, F.; Knobelspiesse, K.; et al. Aerosol retrievals from the ACEPOL Campaign. Atmos. Meas. Tech. Discuss. 2019. [Google Scholar] [CrossRef]
- Giles, D.; Sinyuk, A.; Sorokin, M.; Schafer, J.; Smirnov, A.; Slutsker, I.; Eck, T.; Holben, B.; Lewis, J.; Campbell, J.; et al. Advancements in the Aerosol Robotic Network (AERONET) Version 3 database—Automated near-real-time quality control algorithm with improved cloud screening for Sun photometer aerosol optical depth (AOD) measurements. Atmos. Meas. Tech. 2019, 12, 169–209. [Google Scholar] [CrossRef] [Green Version]
- Holben, B.N.; Tanre, D.; Smirnov, A.; Eck, T.F.; Slutsker, I.; Abuhassan, N.; Newcomb, W.W.; Schafer, J.S.; Chatenet, B.; Lavenu, F.; et al. An emerging ground-based aerosol climatology: Aerosol optical depth from AERONET. J. Geophys. Res. Atmos. 2001, 106, 12067–12097. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef] [Green Version]
- Gelaro, R.; McCarty, W.; Suarez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Statistical Methods for Assessing Agreement between Two Methods of Clinical Measurements. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]








| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | |
|---|---|---|---|---|---|
| 0.094 | 0.163 | 0.282 | 0.882 | 1.759 | |
| 0.130 | 0.130 | 0.130 | 0.284 | 1.718 |
| Parameter in the State Vector | Parametric 5-Mode Retrieval | |
|---|---|---|
| Aerosol properties | Aerosol loading | |
| Spherical index | ||
| Refractive index coefficients | ||
| Aerosol layer height | ||
| Surface properties | Wind speed | |
| Chlorophyll-a concentration | ||
| Lambertian albedo term | ||
| Number of aerosol parameters | 11 | |
| Number of surface parameters | ||
| Length of the state vector |
| Parameters | Range |
|---|---|
| AOD_fine/coarse | 0.005–0.70 |
| Spherical index | 0–1.0 |
| Refractive index coefficients of INOR for fine modes | 0.887–0.975 |
| Refractive index coefficients of BC for fine modes | 0–0.05 |
| Refractive index coefficients of INOR for coarse modes | 0.439–0.512 |
| Refractive index coefficients of DUST for coarse modes | 0.439–0.512 |
| Aerosol layer height (km) | 1.0–6.0 |
| Chlorophyll-a concentration (mg/m3) | 0.001–10.0 |
| USC-SEAPRISM/ SPEX Airborne | τ380 | τ550 | τ670 |
|---|---|---|---|
| Mean AOD(23rd) | 0.0300/0.0631 | 0.0282/0.0554 | 0.0234/0.0487 |
| Mean AOD(25th) | 0.0431/0.0432 | 0.0326/0.0331 | 0.0260/0.0263 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, C.; Fu, G.; Di Noia, A.; Smit, M.; H.H. Rietjens, J.; A. Ferrare, R.; Burton, S.; Li, Z.; P. Hasekamp, O. Use of A Neural Network-Based Ocean Body Radiative Transfer Model for Aerosol Retrievals from Multi-Angle Polarimetric Measurements. Remote Sens. 2019, 11, 2877. https://doi.org/10.3390/rs11232877
Fan C, Fu G, Di Noia A, Smit M, H.H. Rietjens J, A. Ferrare R, Burton S, Li Z, P. Hasekamp O. Use of A Neural Network-Based Ocean Body Radiative Transfer Model for Aerosol Retrievals from Multi-Angle Polarimetric Measurements. Remote Sensing. 2019; 11(23):2877. https://doi.org/10.3390/rs11232877
Chicago/Turabian StyleFan, Cheng, Guangliang Fu, Antonio Di Noia, Martijn Smit, Jeroen H.H. Rietjens, Richard A. Ferrare, Sharon Burton, Zhengqiang Li, and Otto P. Hasekamp. 2019. "Use of A Neural Network-Based Ocean Body Radiative Transfer Model for Aerosol Retrievals from Multi-Angle Polarimetric Measurements" Remote Sensing 11, no. 23: 2877. https://doi.org/10.3390/rs11232877
APA StyleFan, C., Fu, G., Di Noia, A., Smit, M., H.H. Rietjens, J., A. Ferrare, R., Burton, S., Li, Z., & P. Hasekamp, O. (2019). Use of A Neural Network-Based Ocean Body Radiative Transfer Model for Aerosol Retrievals from Multi-Angle Polarimetric Measurements. Remote Sensing, 11(23), 2877. https://doi.org/10.3390/rs11232877