Multiple Kernel Feature Line Embedding for Hyperspectral Image Classification

Abstract

In this study, a novel multple kernel FLE (MKFLE) based on general nearest feature line embedding (FLE) transformation is proposed and applied to classify hyperspectral image (HSI) in which the advantage of multple kernel learning is considered. The FLE has successfully shown its discriminative capability in many applications. However, since the conventional linear-based principle component analysis (PCA) pre-processing method in FLE cannot effectively extract the nonlinear information, the multiple kernel PCA (MKPCA) based on the proposed multple kernel method was proposed to alleviate this problem. The proposed MKFLE dimension reduction framework was performed through two stages. In the first multple kernel PCA (MKPCA) stage, the multple kernel learning method based on between-class distance and support vector machine (SVM) was used to find the kernel weights. Based on these weights, a new weighted kernel function was constructed in a linear combination of some valid kernels. In the second FLE stage, the FLE method, which can preserve the nonlinear manifold structure, was applied for supervised dimension reduction using the kernel obtained in the first stage. The effectiveness of the proposed MKFLE algorithm was measured by comparing with various previous state-of-the-art works on three benchmark data sets. According to the experimental results: the performance of the proposed MKFLE is better than the other methods, and got the accuracy of 83.58%, 91.61%, and 97.68% in Indian Pines, Pavia University, and Pavia City datasets, respectively.

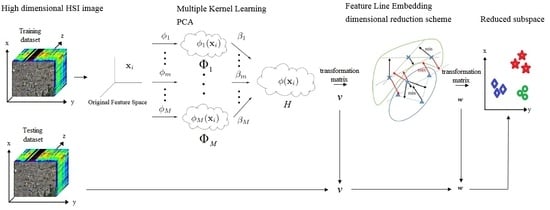
1. Introduction

In this big data era, deep learning has shown its convincing capabilities for providing effective solutions to the crucial areas such as hyperspectral image (HSI) classification [1], object detection [2], and face recognition [3]. Deep learning algorithms can extract substantial information and features from huge amount of data; however, if there is not a suitable dimensionality reduction (DR) algorithm to reduce the dimension of the training data effectively, the performance of deep learning algorithms could be seriously impacted [1]. Therefore, the DR algorithm has potential to improve the performance and explainability of deep learning algorithms.

Since most of the HSI are with high-dimensional spectral and abundant spectral bands, DR in HSI classification has been a critical issue. The major problem is that the spectral patterns of HSI are too similar to identify them clearly. Therefore, a powerful DR which can construct a high-dimensional discriminative space and preserve the manifold of discriminability in low-dimensional space is an essential step for HSI classification.

Recently, abundant DR schemes have been presented which could be grouped into three categories: global-based analysis, local-based analysis, and kernel-based analysis. In the global-based analysis category, those using subtracting the mean of population or mean of class from individual samples to obtain the scatter matrix, and try to extract a projection matrix to minimize or maximize the covariance matrix, include principal component analysis (PCA) [4], linear discriminant analysis (LDA) [5], and discriminant common vectors (DCV) [6]. In these methods, all the scatters of samples are demonstrated in the global Euclidean structure, which means that while samples are distributed in a Gaussian function or are linearly separated, these global-based analysis algorithms demonstrate superior capability in DR or classification. However, while the scatter of samples is distributed in a nonlinear structure, the performance of these global measurement algorithms would be seriously impacted since that in a space with high-dimension, samples’ local structure is not apparent. In addition, the critical issue about global-based analysis methods is that, while the decision boundaries are predominantly nonlinear, the classification performance would decline sharply [7].

In the local-based analysis category, those using subtracting one sample from the other neighboring sample to obtain the scatter matrix, which is also termed manifold learning, can preserve the structure of locality of the samples. He et al. [8] presented the locality preserving projection (LPP) algorithm to keep the structure of locality of training data to identify faces. Because LPP applies the relationship between neighbors to reveal sample scatter, the local manifold of samples is kept and outperforms those in the category of global-based analysis methods. Tu et al. [9] proposed the Laplacian eigenmap (LE) algorithm, in which the polarimetric synthetic aperture radar data were applied to classify the land cover. The LE method preserves the manifold structure of polarimetric space with high-dimension into an intrinsic space with low-dimension. Wang and He [10] applied LPP as a data pre-processing step in classifying HSI. Kim et al. [11] proposed the locally linear embedding (LLE)-based method for DR in HSI. Li et al. [12,13] proposed the local Fisher discriminant analysis (LFDA) algorithm which considers the advantages of LPP and LDA simultaneously for reducing the dimension of HSI. Luo et al. [14] presented a neighborhood preserving embedding (NPE) algorithm, which was a supervised method for extracting salient features for classifying HSI data. Zhang et al. [15] presented a sparse low-rank approximation algorithm for manifold regularization, which takes the HSI as cube data for classification. These local-based analysis schemes all preserve the manifold of samples and outperform the conventional global-based analysis methods.

The kernel-based analysis category, in spite of the local-based analysis methods, has achieved a better result than those global-based ones. However, based on Boots and Gordon [16], the practical application of manifold learning was still constrained by noises due to that the manifold learning could not extract nonlinear information. Therefore, those using the idea of kernel tricks to generate nonlinear feature space and improve extracting the nonlinear information are kernel-based analysis methods. Since a suitable kernel function could improve a given method on performance [17]. Therefore, both categories of global-based and local-based analysis methods adopted the kernelization approaches to improve the performance of classifying HSI. Boots and Gordon [16] investigated the kernelization algorithm to mitigate the effect of noise to manifold learning. Scholkopf et al. [18] presented a kernelization PCA (KPCA) algorithm which can find a high-dimensional Hilbert space via kernel function and extract the salient non-linear features that PCA missed. In addition to single kernel, Lin et al. [19] proposed a multiple kernel learning algorithm for DR. The multiple kernel function was integrated, and the revealed multiple feature of data was shown in a low dimensional space. However, it tried to find suitable weights for kernels and DR simultaneously, which leads to a more complicated method. Therefore, Nazarpour and Adibi [20] proposed a kernel learning algorithm concentrating only on learning good kernel from some basic kernel. Although this method proposed an effective, simple idea for multiple kernel learning, it applied the global-based kernel discriminant analysis (KDA) method for classification, therefore, it could not preserve the manifold structure of high dimensional multiple kernel space; moreover, a combined kernel scheme, where multiple kernels were linearly assembled to extract both spatial and spectral information [21]. Chen et al. [22] proposed a kernel method based on sparse representation to classify HSI data. A query sample was revealed by all training data in a generated kernel space, and pixels in a neighboring area were also described by all training samples in a linear combination. Resembling the multiple kernel method, Zhang et al. [23] presented a multiple-features assembling algorithm for classifying HSI data, which integrated texture, shape, and spectral information to improve the performance of HSI classification.

In previous works, the idea of nearest feature line embedding (FLE) was successfully applied in reducing dimension on face recognition [24] and classifying HSI [25]. However, the abundant nonlinear structures and information could not be efficiently extracted using only the linear transformation and single kernel. Multple kernel learning is an effective tool for enhancing the nonlinear spaces by integrating many kernels into a new consistent kernel. In this study, a general nearest FLE transformation, termed multple kernel FLE (MKFLE), was proposed for feature extraction (FE) and DR in which multiple kernel functions were simultaneously considered. In addition, the support vector machine (SVM) was applied in the proposed multiple kernel learning strategy which uses only the support vector set to determine the weight of each valid kernel function. Moreover, three benchmark data sets were evaluated in the experimental analysis in this work. The performance of the proposed algorithm was evaluated by comparison with state-of-the-art methods.

The rest of this study is organized as follows: The related works are reviewed in Section 2. The proposed multple kernel learning method is introduced and incorporated into the FLE algorithm in Section 3. Some experimental results and comparisons with some state-of-the-art algorithms for classifying HSI are conducted to demonstrate the effectiveness of the proposed algorithm as introduced in Section 4. Finally, in Section 5, conclusions are given.

2. Related Works

In this paper, FLE [24,25] and multple kernel learning were integrated to reduce the dimensions of features for classifying the HSI data. A brief review of FLE, kernelization, and multple kernel learning are introduced in the following before the proposed methods. Assume that $N$ $d$-dimensional training data $X=\left[x_1,x_2,\dots ,x_N\right]\in R^{d\times N}$ consisting of $N_C$ land-cover classes $C_1,C_2,\dots ,C_{N_C}$. The projected samples in low-dimensional space could be obtained by the linear projection $y_i=w^T{x}_i$, where $w$ is an obtained linear transformation for dimension reduction.

2.1. Feature Line Embedding (FLE)

FLE is a local-based analysis for DR in which the sample data scatters could be shown in a form of Laplacian matrix to preserve the locality by applying the strategy of point-to-line. The cost function of FLE is minimized and defined as follows:

$$\begin{array}{lll}O& =& {{\displaystyle \sum }}_i\left({{\displaystyle \sum }}_{i\ne m\ne n}\Vert y_i-L_{m,n}\left(y_i\right){\Vert }^2{l}_{m,n}\left(y_i\right)\right)\\ O& =& {\displaystyle \sum _i}\left({\displaystyle \sum _{i\ne m\ne n}}\Vert y_i-L_{m,n}\left(y_i\right){\Vert }^2{l}_{m,n}\left(y_i\right)\right)\\ & =& {\displaystyle \sum _i}\Vert y_i-{\displaystyle \sum _j}{M}_{i,j}{y}_j{\Vert }^2\\ & =& \rightleftarrows tr\left(Y{\left(I-M\right)}^T\left(I-M\right)Y\right)=tr\left(w^{T}X\left(D-W\right)X^{T}w\right)\\ & =& tr\left(w^{T}XL{X}^{T}w\right),\end{array}$$

(1)

where point $L_{m,n}\left(y_i\right)$ is a projection sample on line $L_{m,n}$ for sample $y_i$, and weight $l_{m,n}\left(y_i\right)$ (being 0 or 1) describes the connection between point $y_i$ and the feature line $L_{m,n}$ which two samples $y_m$ and $y_n$ passes through. The projection sample $L_{m,n}\left(y_i\right)$ is described as a linear combination of points $y_m$ and $y_n$:$L_{m,n}\left(y_i\right)=y_m+t_{m,n}\left(y_n-y_m\right)$, that $t_{m,n}={\left(y_i-y_m\right)}^T\left(y_m-y_n\right)/{\left(y_m-y_n\right)}^T\left(y_m-y_n\right)$, and $i\ne m\ne n$. Applying some simple operations of algebra, the discriminant vector from sample $y_i$ to the projection sample $L_{m,n}\left(y_i\right)$. could be described as $y_i-{\displaystyle \sum }_j{M}_{i,j}{y}_j$, where two elements in the $i$th row in matrix $M$ are viewed as $M_{i,m}=t_{n,m}$, $M_{i,n}=t_{m,n}$, and $t_{n,m}+t_{m,n}=1$, while weight $l_{m,n}\left(y_i\right)=1$. The other elements in the i’th row are set as 0, if $j\ne m\ne n$. In Equation (1), the mean of squared distance for all training data samples to their nearest feature lines (NFLs) is then extracted as $tr\left(w^{T}XL{X}^{T}w\right)$, that $L=D-W$, and matrix $D$ expresses the column sums of the similarity matrix $W$. According to the summary of Yan et al. [26], matrix $W$ is expressed as $W_{i,j}={\left(M+M^T-M^{T}M\right)}_{i,j},$ while $i\ne j$ is zero otherwise; ${\displaystyle \sum }_j{M}_{i,j}{y}_j=1$. Matrix $L$ in Equation (1) could be expressed as a Laplacian form. More details could be referred to [24,25].

In supervised FLE, the label information is considered, and there are two parameters, $N_1$ and $N_2,$ determined manually in obtaining the within-class matrix $S_{FLEw}$ and the between-class matrix $S_{FLEb}$, respectively:

$${\mathit{S}}_{FLEw}={{\displaystyle \sum }}_{c=1}^{N_C}\left({{\displaystyle \sum }}_{x_i\in C_c}{{\displaystyle \sum }}_{L_{m,n}\in F_{N_1}\left(x_i,C_c\right)}\left(x_i-L_{m,n}\left(x_i\right)\right)\left(x_i-L_{m,n}\left(x_i\right)\right){}^T\right),\mathrm{and}$$

(2)

$${\mathit{S}}_{FLEb}={{\displaystyle \sum }}_{c=1}^{N_C}\left({{\displaystyle \sum }}_{x_i\in C_c}{{\displaystyle \sum }}_{l=1,l\ne c}^{N_C}{{\displaystyle \sum }}_{L_{m,n}\in F_{N_2}\left(x_i,C_l\right)}\left(x_i-L_{m,n}\left(x_i\right)\right)\left(x_i-L_{m,n}\left(x_i\right)\right){}^T\right),$$

(3)

where $F_{N_1}\left(x_i,C_k\right)$ represents the set of $N_1$ NFLs within the same class, $C_c$, of point $x_i$, i.e., $l_{m,n}\left(y_i\right)=1$, and $F_{K_2}\left(x_i,C_l\right)$ is a set of $N_2$ NFLs from different classes of point $x_i$. Then, the Fisher criterion $tr\left(w^T{S}_{FLEb}w/w^T{S}_{FLEw}w\right)$ is applied to be maximized and extract the transformation matrix $w$, which is constructed of the eigenvectors with the corresponding largest eigenvalues. Finally, a new sample in the low-dimensional space can be represented by the linear projection $y=w^{T}x$, and the nearest neighbor (one-NN) template matching rule is used for classification.

2.2. Kernelization

Kernelization is a function that maps a linear space $X$ to a nonlinear Hilbert space $H$, $\phi :x\in X\to \phi \left(x\right)\in H$, the conventional within-class and between-class matrix of LDA in space $H$ can be represented as:

$${\mathit{S}}_{LDAw}^{\phi }={{\displaystyle \sum }}_{k=1}^{N_C}\left({{\displaystyle \sum }}_{x_i\in C_k}\left(\phi \left(x_i\right)-{\overline{\phi }}_k\right){\left(\phi \left(x_i\right)-{\overline{\phi }}_k\right)}^T\right),\mathrm{and}$$

(4)

$${\mathit{S}}_{LDAb}^{\phi }={\displaystyle \sum }_{k=1}^{N_C}\left({\overline{\phi }}_k-\overline{\phi }\right){\left({\overline{\phi }}_k-\overline{\phi }\right)}^T.$$

(5)

Here, ${\overline{\phi }}_k=\frac{1}{n_k}{\displaystyle \sum }_{i=1}^{n_k}\phi \left(x_i\right)$ and ${\overline{\phi }}_{}=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\phi \left(x_i\right)$ indicate mean of the class and mean of population in space $H$, respectively. In order to generalize the within-class and between-class scatters to the nonlinear version, the dot product kernel trick is used exclusively. The representation of dot product on the Hilbert space $H$ is given by the kernel function in the following: $k\left(x_i,x_j\right)=k_{i,j}={\phi }^T\left(x_i\right)\phi \left(x_j\right)$. Considering the symmetric matrix $K$ of $N$ by $N$ be a matrix constructed by dot product in high dimensional feature space $H$, i.e., $K\left(x_i,x_j\right)=\langle \phi \left(x_i\right)\cdot \phi \left(x_j\right)\rangle =\left(k_{i,j}\right)$ and, $i,j=1,2,\dots ,N$. Based on the kernel trick, the kernel operator $K$ makes the development of the linear separation function in space $H$ to be equivalent to that of the nonlinear separation function in space $X$. Kernelization can be applied in maximizing the between-class matrix and minimizing the within-class matrix, too, i.e., $max\left(w^T{S}_{LDAb}^{\phi }w/w^T{S}_{LDAw}^{\phi }w\right)$. This maximization is equal to the conventional eigenvector resolution: $\lambda S_{LDAw}^{\phi }w=S_{LDAb}^{\phi }w$, in which a set of eigenvalue $\alpha$ for $w={\displaystyle \sum }_{i=1}^N{\alpha }_i\phi \left(x_i\right)$ can be found so that the largest one obtains the maximum of the matrix quotient $\lambda =w^T{S}_{LDAb}^{\phi }w/w^T{S}_{LDAw}^{\phi }w$.

3. Multiple Kernel Feature Line Embedding (MKFLE)

Based on the analyses mentioned above, a suitable DR scheme can effectively generate discriminant non-linear space and preserve the discriminability of manifold structure into low dimensional feature space. Therefore, multiple kernel feature line embedding (MKFLE) was presented for classifying the HSI. The original idea of MKFLE is integrating the multiple kernel learning with the manifold learning method. The combination of multiple kernels not only effectively constructs the manifold of the original data from multiple views, but also increases the discriminability for DR. Then, the following manifold learning-based FLE scheme preserves the locality information of samples in the constructed Hilbert space. FLE has been applied in classifying HSI successfully. High-degree non-linear data geometry limits the effectiveness of locality preservation of manifold learning. Therefore, multiple kernel learning is applied as introduced in the following to mitigate the problem.

3.1. Multiple Kernel Principle Component Analysis (MKPCA)

In general, the multiple kernel learning is to transform the representation of samples in original feature space into the optimization of weights ${\left\{{\beta }_m\right\}}_{m=1}^M$ for a valid set of basic kernels ${\left\{k_m\right\}}_{m=1}^M$ based on their importance. The aim is to construct a new kernel $K$ via a linear combination of valid kernels as follows:

$$K={\displaystyle \sum }_{m=1}^M{\beta }_m{k}_m,{\beta }_m\ge 0\mathrm{and}{\displaystyle \sum }_{m=1}^M{\beta }_m=1.$$

(6)

Then, a new constructed combined kernels function can be described as below:

$$k\left(x_i,x_j\right)={\displaystyle \sum }_{m=1}^M{\beta }_m{k}_m\left(x_i,x_j\right),{\beta }_m\ge 0.$$

(7)

In this study, eight kernel functions all of the type Radial basis function (RBF), but with different distance functions and different parameters, are used as basic kernels. Therefore, there is no need to perform the kernel alignment or unify different kernels into the same dimension. While the optimization weights ${\left\{{\beta }_m\right\}}_{m=1}^M$ are determined, a new constructed kernel $K$ would be obtained. Let $\phi :x\in X\to \phi \left(x\right)\in H$ be a mapping function of kernel $K$ from feature space in low-dimension to Hilbert space $H$ in high-dimension. Denote $\Phi =\left[\phi \left(x_1\right),\phi \left(x_2\right),\dots ,\phi \left(x_N\right)\right]$, and $\overline{\phi }=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\phi \left(x_i\right)$. Without loss of generality, suppose that the training data are normalized in $H$, i.e., $\overline{\phi }=0$, then the total scatter matrix is described as ${\mathit{S}}_t^{\phi }={\displaystyle \sum }_{i=1}^N\left({\phi }_i-\overline{\phi }\right){\left({\phi }_i-\overline{\phi }\right)}^T=\Phi {\Phi }^T$. In the proposed MKPCA, the criterion demonstrated in Equation (8) is applied to extract the optimal projective vector $v$:

$$J\left(v\right)={\displaystyle \sum }_{i=1}^N\Vert v^T\phi \left(x_i\right)\Vert =v^T{\mathit{S}}_t^{\phi }v.$$

(8)

Then the solution for Equation (8) would be the eigenvalue problem: $\lambda v={\mathit{S}}_t^{\phi }v$ where $\lambda \ge 0$ and eigenvectors $v\in H$. Therefore, Equation (8) could be described as an equal problem:

$$\lambda q=Kq,$$

(9)

in which $K={\Phi }^T\Phi$ is the kernel matrix. Assuming that $\left\{q_1,q_2,\dots q_b\right\}$ are the corresponding $b$ eigenvalues to the Equation (9); then $v_i=\Phi q_i$ is the solution of Equation (8). Since the proposed MKPCA algorithm is a kind of modified KPCA, its kernel is a constructed ensemble of multiple kernels via a learned weighted combination. Therefore, the MKPCA based FE or DR needs only kernel functions in the input space instead of applying any nonlinear mapping $\phi$ as kernel method. Furthermore, since each different data set has the nature of data itself, applying a fixed ensemble kernel for different applications would limit the performance. Therefore, an optimal weighted combination of all valid subkernels based on their separability is introduced in the following.

3.2. Multiple Kernel Learning based on Between-Class Distance and Support Vector Machine

In the proposed MKPCA, the new ensemble kernel function $K$ applied in Equation (6) is obtained through a linear combination of $M$ valid subkernel function, and ${\beta }_m$ is the weight of ‘$m\prime$th subkernel in the combination, which should be learned from the training data. Applying multiple kernels improves to extract the most suitable kernel function for the data of different applications. In this study, a new multiple kernel learning method is proposed to determine the kernel weight vector $\mathit{\beta }=\left[{\beta }_1,{\beta }_2,\dots ,{\beta }_M\right]$ based on the between-class distance and SVM.

Since the goal of the proposed MKFLE is for discrimination, our idea for optimization of the kernel weight vector $\mathit{\beta }$ is based on the maximizing between-class distance criterion as follows:

$$J_1\left(\mathit{\beta }\right)=tr\left({\mathit{S}}_b^{\phi }\right),$$

(10)

with

$$tr\left({\mathit{S}}_b^{\phi }\right)=tr\left({\displaystyle \sum }_{i=1}^{N_c-1}{\displaystyle \sum }_{j=i+1}^{N_c}\left({\overline{\phi }}_i-{\overline{\phi }}_j\right){\left({\overline{\phi }}_i-{\overline{\phi }}_j\right)}^T\right).$$

(11)

With $tr\left(AB\right)=tr\left(BA\right)$, Equation (11) could be described as follows:

$$\begin{array}{l}tr\left({\mathit{S}}_b^{\phi }\right)={\displaystyle \sum _{i=1}^{N_c-1}}{\displaystyle \sum _{j=i+1}^{N_c}}{\left({\overline{\phi }}_i-{\overline{\phi }}_j\right)}^T\left({\overline{\phi }}_i-{\overline{\phi }}_j\right)\\ \rightleftarrows ={\displaystyle \sum _{i=1}^{N_c-1}}{\displaystyle \sum _{j=i+1}^{N_c}}{r}_i{r}_j\left[1_i^T{K}_{i,i}{1}_i-{21}_i^T{K}_{i,j}{1}_j+1_j^T{K}_{j,j}{1}_j\right]\\ \rightleftarrows ={\displaystyle \sum _{m=1}^M}{\displaystyle \sum _{i=1}^{N_c-1}}{\displaystyle \sum _{j=i+1}^{N_c}}{r}_i{r}_j\left[1_i^T{K}_{i,i}^m{1}_i-{21}_i^T{K}_{i,j}^m{1}_j+1_j^T{K}_{j,j}^m{1}_j\right]{\beta }_m=B^T\mathit{\beta },\end{array}$$

(12)

in which $r_i=n_i/N$, $n_i$ is the amount of samples in i’th class, and $K_{i,j}$, $K_{i,j}^m$, $1_i$, are described as follows:

$$K_{i,j}={\displaystyle \sum }_{m=1}^M{\beta }_m{K}_{i,j}^m,{\beta }_m\ge 0\mathrm{and}{\displaystyle \sum }_{m=1}^M{\beta }_m=1,$$

(13)

$$K_{i,j}^m=\left[\begin{array}{ccc}{k}_m\left(x_1^i,x_1^j\right)& \cdots & k_m\left(x_1^i,x_{n_j}^j\right)\\ ⋮& \ddots & ⋮\\ k_m\left(x_{n_i}^i,x_1^j\right)& \cdots & k_m\left(x_{n_i}^i,x_{n_j}^j\right)\end{array}\right],$$

(14)

$$1_i={\left[\begin{array}{c}1/n_i\\ ⋮\\ 1/n_i\end{array}\right]}_{n_i\times 1},$$

(15)

where $B$ is a $M\times 1$ vector, in which the elements are the traces of the between-class matrices of $M$ different kernels, and $\mathit{\beta }$ is a vector, in which the elements are the weights of subkernels.

The between-class distance is well for measurement of discrimination, however, while the $n_i$ and $n_j$ increase, the generalization of ${\overline{\phi }}_i-{\overline{\phi }}_j$ would decrease. To solve this problem, inspired from the SVM, support vectors between two classes are taken into consideration for computation of the between-class distance. In other words, since the support vectors are much more representative of the class for discrimination, only the support vectors between two classes are used for computation of the between-class distance to improve the generalization of ${\overline{\phi }}_i-{\overline{\phi }}_j$. Thus, based on the criterion in Equation (10), the integration of between-class distance and SVM is used as a criterion to find the optimal $\mathit{\beta }$, defined as follow:

$$J_2\left(\mathit{\beta }\right)=tr\left({\mathit{S}}_b^{\phi SV}\right),$$

(16)

where ${\mathit{S}}_b^{\phi SV}$ is the between-scatter matrix formed by the support vectors between classes. Therefore, in a similar manner, the optimization problem in Equation (12) could be re-described as follows:

$$tr\left({\mathit{S}}_b^{\phi SV}\right)={\displaystyle \sum }_{m=1}^M{\displaystyle \sum }_{i=1}^{N_c-1}{\displaystyle \sum }_{j=i+1}^{N_c}{r}_i^{SV}{r}_j^{SV}\left[1_i^{TSV}{K}_{i,i}^{mSV}{1}_i^{SV}-{21}_i^{TSV}{K}_{i,j}^{mSV}{1}_j^{SV}+1_j^{TSV}{K}_{j,j}^{mSV}{1}_j^{SV}\right]{\beta }_m=B^T\mathit{\beta },$$

(17)

where $r_i^{SV}=n_i^{SV}/N^{SV}$, $n_i^{SV}$ is the amount of support vectors of i’th class, and $N^{SV}$ is the amount of support vectors in all classes. The difference between criterion $J_2\left(\mathit{\beta }\right)$ and $J_1\left(\mathit{\beta }\right)$ is that the $J_2\left(\mathit{\beta }\right)$ applies only the support vectors between classes while the $J_1\left(\mathit{\beta }\right)$ uses all samples in the classes. Using Equation (17), the optimization problem is formulated as follows:

$$\underset{\mathit{\beta }}{max}{B}^T\mathit{\beta },\mathrm{subject}\mathrm{to}{\beta }_m\ge 0\mathrm{and}{\displaystyle \sum _{m=1}^M}{\beta }_m=1.$$

(18)

In the optimization problem mentioned in Equation (18), each kernel is supposed to be a Mercer kernel. Therefore, the linear combination of these kernels is still a Mercer kernel. In addition, the sum of these weights is subject to be equal to one. Thus, the optimization problem of (18) is a linear programming (LP) problem which could be solved by a Lagrange optimization procedure. In this study, the proposed MKPCA applies $J_2\left(\mathit{\beta }\right)$ as multiple kernel learning criterion to find the optimal weights for subkernels.

In addition, radial basis function (RBF) kernel with Euclidian distance is applied as the kernel function of the method of single kernel function, such as Fuzzy Kernel Nearest Feature Line Embedding (FKNFLE), and KNFLE in [25]. In the proposed MKL scheme, eight kernel functions all of the RBF type [20] are applied with different distance measurements and different kernel parameters. The RBF kernel is defined as follows:

$$K_m\left(i,j\right)=k_m\left(x_i,x_j\right)=exp\left(\frac{-d_m^2\left(x_i,x_j\right)}{{\sigma }_m^2}\right),$$

(19)

where $d\left(.,.\right)$ represents the distance function. There are four distance functions applied in the proposed MKL scheme, the first is the Euclidean distance function as follows:

$$d_m\left(x_i,x_j\right)=\sqrt{{\left(x_i^1-x_j^1\right)}^2+\cdots {\left(x_i^d-x_j^d\right)}^2}.$$

(20)

The second is the L1 distance function defined as follows:

$$d_m\left(x_i,x_j\right)={\displaystyle \sum }_{l=1}^d\left|x_i^l-x_j^l\right|.$$

(21)

The third is the cosine distance function defined as follows:

$$d_m\left(x_i,x_j\right)=cos\left(\theta \right)=\frac{x_i·x_j}{\Vert x_i\Vert \Vert x_j\Vert }.$$

(22)

The fourth is the Chi-squared distance function defined as follows:

$$d_m\left(x_i,x_j\right)={\displaystyle \sum }_{l=1}^d\frac{{\left(x_i^1-x_j^1\right)}^2}{{\left(x_i^1+x_j^1\right)}^2}.$$

(23)

In Equation (19), ${\sigma }_m$ is the kernel parameter, which could be obtained by the method in [20]. In this study, four kernels of Equations (20)–(23), their kernel parameter ${\sigma }_m$ are obtained by homoscedasticity method [20], and the other four kernels also apply the Equations (20)–(23) but with the mean of all distances as kernel parameters.

3.3. Kernelization of FLE

In the proposed MKFLE algorithm, the MKPCA is firstly performed to construct the new kernel via the proposed multiple kernel learning method. Then, all training points are projected into the Hilbert space $H$ based on the new ensemble kernel. After that, the FLE algorithm based on the manifold learning is performed to compute the mean of squared distance for total training samples to their nearest feature lines in high-dimensional Hilbert space, and which can be expressed as follows:

$$\begin{array}{l}{\displaystyle \sum _i}\Vert \phi \left(y_i\right)-L_{m,n}\left(\phi \left(y_i\right)\right){\Vert }^{\left(2\right)}={\displaystyle \sum _i}\Vert \phi \left(y_i\right)-{\displaystyle \sum _j}{M}_{i,j}\phi \left(y_j\right){\Vert }^2\\ \rightleftarrows \rightleftarrows \rightleftarrows \rightleftarrows =tr\left({\phi }^T\left(Y\right){\left(I-M\right)}^T\left(I-M\right)\phi \left(Y\right)\right)\\ \rightleftarrows \rightleftarrows =tr\left({\phi }^T\left(Y\right)\left(D-W\right)\phi \left(Y\right)\right)\\ \rightleftarrows \rightleftarrows \rightleftarrows \rightleftarrows \rightleftarrows =tr\left(w^T\phi \left(X\right)L{\phi }^T\left(X\right)w\right).\end{array}$$

(24)

Then, the object function in Equation (24) could be described as a minimum problem and represented in a Laplacian form. The eigenvector problem of kernel FLE in the Hilbert space is represented as:

$$\left[\phi \left(X\right)L{\phi }^T\left(X\right)\right]w=\lambda \left[\phi \left(X\right)D{\phi }^T\left(X\right)\right]w.$$

(25)

To expand the applications of FLE algorithm to kernel FLE, the implicit feature vector, $\phi \left(x\right)$, has no necessity to be calculated practically. The inner product representation of two data points in the Hilbert space is exclusively used with a kernel function as follows: $K\left(x_i,x_j\right)=\langle \phi \left(x_i\right),\phi \left(x_j\right)\rangle$. The eigenvectors of Equation (25) are described by the linear combinations of $\phi \left(x_1\right)$, $\phi \left(x_2\right)$,$\dots$, $\phi \left(x_N\right)$. The coefficient ${\alpha }_i$ is $w={\displaystyle \sum }_{i=1}^N{\alpha }_i\phi \left(x_i\right)=\phi \left(X\right)\mathit{\alpha }$ where $\mathit{\alpha }={\left[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_N\right]}^T\in R^N$. Then, the eigenvector problem is represented as follows:

$$KLK\alpha =\lambda KDK\alpha .$$

(26)

Assuming that the solutions of Equation (26) are the coefficient vectors, ${\alpha }^1,{\alpha }^2,\dots ,{\alpha }^N$ in a column format. Given a querying sample, $z$, and its projection on the eigenvectors, $w^k$, are computed by the following equation:

$$\left(w^k\cdot \phi \left(z\right)\right)={{\displaystyle \sum }}_{i=1}^N{\alpha }_i^k\langle \phi \left(z\right),\phi \left(x_i\right)\rangle ={{\displaystyle \sum }}_{i=1}^N{\alpha }_i^{k}K\left(z,x_i\right),$$

(27)

where ${\alpha }_i^k$ is the ith element of the coefficient vector, ${\alpha }^k$. The kernel function RBF (radial basis function) is used in this study. Thus, the within-class scatters and the between-class scatters in a kernel space are defined as follows:

$$\begin{gathered} {\mathit{S}}_{FLEw}^{\phi }={{\displaystyle \sum }}_{c=1}^{N_C}\left({{\displaystyle \sum }}_{\phi \left(x_i\right)\in C_c}{{\displaystyle \sum }}_{L_{m,n}\in F_{N_1}\left(\phi \left(x_i\right),C_c\right)}\left(\phi \left(x_i\right)-L_{m,n}\left(\phi \left(x_i\right)\right)\right)\left(\phi \left(x_i\right)-L_{m,n}\left(\phi \left(x_i\right)\right)\right){}^T\right), \\ \mathrm{and} \end{gathered}$$

(28)

$${\mathit{S}}_{FLEb}^{\phi }={{\displaystyle \sum }}_{c=1}^{N_C}\left({{\displaystyle \sum }}_{\phi \left(x_i\right)\in C_c}{{\displaystyle \sum }}_{l=1,l\ne c}^{N_C}{{\displaystyle \sum }}_{L_{m,n}\in F_{N_2}\left(\phi \left(x_i\right),C_l\right)}\left(\phi \left(x_i\right)-L_{m,n}\left(\phi \left(x_i\right)\right)\right)\left(\phi \left(x_i\right)-L_{m,n}\left(\phi \left(x_i\right)\right)\right){}^T\right).$$

(29)

Since the Hilbert space $H$ constructed by the proposed MKPCA is an ensemble kernel space from multiple subkernels, there would be abundant useful non-linear information from different views for discrimination. Hence, applying the kernelized FLE to preserve those non-linear local structure in MKPCA would improve the performance of FE and DR. The pseudo-codes of the proposed MKFLE algorithm are tabulated in

Table 1. The procedures of MKFLE (multple kernel feature line embedding) algorithm.

Input:	A $d$ -dimensional training data $X=\left[x_1,x_2,\dots ,x_N\right]$ consists of Nc classes.
Output:	The projection transformation $w$.
Step 1:	Create $M$ kernels using Equation (19).
Step 2:	Apply the SVM algorithm to extract support vectors between classes for the criterion (16).
Step 3:	Determine the vector $\mathit{\beta }$ via solving the LP optimization problem of Equation (18).
Step 4:	Create a new kernel as linear combination of subkernels using Equation (7).
Step 5:	Project the $X$ into the new created kernel space $\phi \left(X\right)=\left[\phi \left(x_1\right),\phi \left(x_2\right),\dots ,\phi \left(x_N\right)\right]$.
Step 6:	PCA projection: Data points are projected from a space with high-dimension into a subspace with low-dimension by matrix $w_{PCA}$.
Step 7:	Calculation of the within-class matrix and between-class matrix using Equations (28) and (29), respectively.
Step 8:	Maximization of Fisher criterion: Fisher criterion $w^{*}=argmax{\mathit{S}}_{FLEb}^{\phi }/{\mathit{S}}_{FLEw}^{\phi }$ is maximized to extract the best projection matrix, which is composed of $\gamma$ eigenvectors with the largest eigenvalues.
Step 9:	Output the projection matrix: $w=w_{PCA}{w}^{*}$.

. In this study, it is proposed that a general form of the FLE method using the SVM-based multple kernel learning be used for FE and DR. The benefits of the proposed MKFLE are twofold: the multple kernel learning scheme based on the SVM strategy can generalize the optimal combination of weights; and the kernelized FLE algorithm based on the manifold learning can preserve the local structure information in high dimensional constructed multple kernel space as well as the manifold local structure in the dimension reduced space.

4. Experimental Results

4.1. Data Sets Description

In this sub-section, in order to evaluate the effectiveness of the proposed MKFLE algorithm, some experimental results are conducted for classifying HSI. Three classic HSI benchmarks are applied for evaluation. The use-case of the three chosen images for evaluation are framed into the HSI analysis for land covers. The first data set was obtained from AVIRIS (Airborne Visible/Infrared Imaging Spectrometer), obtained by the Jet Propulsion Laboratory and NASA/Ames in 1992, and termed Indian Pines Site (IPS) image. This IPS image was collected from six miles in the western area of Northwest Tippecanoe County (NTC). A false color IR image of IPS dataset was shown in Figure 1a. The are 16 land-cover classes with 220 bands in the IPS dataset, e.g., Corn-notill(1428), Alfalfa(46), Corn(237), Corn-mintill(830), Grass-pasture(483), Grass-trees(730), Grass-pasture-mowed(28), Hay-windrowed(478), Oats(20), Soybeans-notill(972), Soybeans-mintill(2455), Soybeans-cleantill(593), Woods(1265), Wheat(205), Stone-Steel-Towers(93), and Bldg-Grass-Tree-Drives(386). The numbers shown in the parentheses were the pixel numbers in this IPS dataset. There were 10,249 pixels in the IPS dataset, and the ground truths for each pixel were labeled manually for testing and training. To evaluate the effectiveness of various algorithms, 10 classes with more than 300 samples were used in the experiments, e.g., a subset IPS-10 of 9620 pixels. There were nine hundred training samples in this IPS-10 subset chosen randomly from 9620 pixels, and the other remaining samples were applied for testing. In addition, all the tests were executed on a twelve-core intel i7-8700k CPU, Matlab (Mathworks) 2016b, Microsoft Win10, and 32gb ram.

The other two data sets, Pavia University, and Pavia City Center, were both the scenes covering the City of Pavia, Italy, obtained from the Reflective Optics System Imaging Spectrometer (ROSIS). They have 103 and 102 data bands, both with a spatial resolution of 1.3 m and a spectral coverage from 0.43 to 0.86 um. The dimension of these two images were 610 × 340 and 1096 × 715 pixels, respectively. The false color IR image of these two image were illustrated as Figure 1b,c. There were nine land-cover classes in each data set, and in each data set, the samples were divided into training and testing part, respectively. For example, in the Pavia University data set, there were 90 training samples in each class selected randomly for training, and the remaining 8046 samples were used for testing the performance. Based on the same manner, there were 810 training and 9529 testing samples used for the Pavia City Center data set, respectively.

4.2. Classification Results

The proposed MKFLE algorithm was compared with three state-of-the-art schemes, i.e., KNFLE, FNFLE, and FKNFLE [25]. The training samples were chosen randomly for computation of the transformation matrix, and the testing samples were applied to the nearest neighbor (NN) matching rule to matched with the training samples. The obtained average rates for each algorithm were run 30 times. In order to extract the suitable reduced dimensions of MKFLE, the obtained training samples were applied to measure the reduced dimensions versus the overall accuracy (OA) in the experimental datasets. As demonstration in Figure 2, the proposed MKFLE for datasets IPS-10, Pavia University, and Pavia City Center has the most suitable dimensions in 25, 65, and 65, respectively. From the classification results as shown in Figure 2, the proposed MKFLE outperforms all the other algorithms at the specific reduced dimensions on three datasets and with lower variant OA rates than the single kernel-based FKNFLE algorithm, which demonstrates the effectiveness of the proposed MKFLE. Based on observing Figure 2, a simple analysis was also done. When only fuzzy or single kernel method was applied in FLE, such as FNFLE and KNFLE, both of them obtained lower variant OA rates, and the kernel method was much more helpful than the fuzzy method since KNFLE outperformed FNFLE. Although FKNFLE outperformed the FNFLE and KNFLE, the variant OA of FKNFLE is large. Since the FKNFLE combined two different types of nonlinear and non-Euclidean information, it might cause the higher variant OA rates. In the meanwhile, multiple kernels applied in the proposed MKFLE used only nonlinear information with various parameters, which could improve the performance and obtain lower variant OA rates. In addition, since the MKL strategy was applied in the MKFLE training phases, which embedded different views of manifold structures from multiple kernel feature space, the reduced space obtained by the proposed MKFLE could be more general than FKNFLE, and obtained lower variant OA rates. From this analysis, the proposed MKFLE is much more superior than the FKNFLE, KNFLE, and FNFLE in HSI classification.

Figure 3a shows the effect of changing the number of training samples on the average classification rates on dataset IPS-10; the proposed MKFLE algorithm has better performance than the other algorithms. The accuracy of MKFLE was 0.24% better than that of FKNFLE, which demonstrates that the proposed MKL strategy effectively enhanced the discriminative power of FLE. Figure 3b,c also shows the effect of changing the number of training samples on the overall accuracy on the benchmark datasets of Pavia University and Pavia City Center, respectively. Based on the overall accuracy in these two datasets, the proposed algorithm MKFLE outperforms the other algorithms. Next, Figure 4 demonstrates the classification results maps for the IPS-10 dataset. The various algorithms MKFLE, FKNFLE, KNFLE, and FNFLE are performed and obtained classification results on the maps of 145 × 145 pixels describing the ground truth. The proposed MKFLE obtained fewer speckle-like errors than those of the other algorithms. In the same manner, Figure 5 and Figure 6 demonstrate the classification results maps for Pavia University and Pavia City Center datasets, respectively. Similarly, the proposed MKFLE obtained fewer speckle-like errors than in the case of the other algorithms.

Moreover, in order to evaluate the performance of the proposed MKFLE algorithm, the user’s accuracy, producer’s accuracy, kappa coefficients, and overall accuracy which were defined by the error matrices (or confusion matrices) [27] were tabulated in

Table 2. The error matrix of classification for the IPS-10 dataset (in percentage).

Classes	Reference Data										User’s Accuracy
	1	2	3	4	5	6	7	8	9	10
1	79.45	3.25	0.21	0.35	0	5.46	9.73	1.54	0	0	79.45
2	5.90	82.04	0	0.12	0	1.33	6.25	4.24	0	0.12	82.04
3	0	0	96.73	1.21	0.21	0.41	0	0.21	0.42	0.81	96.73
4	0	0	0.23	96.54	0	0	0	0	0	3.22	96.54
5	0	0	0.42	0	99.58	0	0	0	0	0	99.58
6	5.04	0.21	0.10	0.41	0	89.09	4.32	0.72	0	0.10	89.09
7	10.58	5.54	0.29	0.33	0.04	9.58	70.22	3.30	0	0.12	70.22
8	1.35	4.03	1.52	0.34	0	1.69	1.65	88.75	0	0.67	88.75
9	0	0	3.27	0.16	0	0	0	0	90.98	5.59	90.98
10	0	0	3.89	5.50	0	0	0	0.26	10.83	79.52	79.52
Producer’s Accuracy	77.64	86.29	90.69	91.97	99.75	82.82	76.18	89.62	88.99	88.20
Kappa Coefficient: 0.829						Overall Accuracy: 83.58%

,

Table 3. The error matrix of classification for the Pavia University dataset (in percentage).

Classes	Reference Data									User’s Accuracy
	1	2	3	4	5	6	7	8	9
1	90.18	3.15	0	0	0	3.24	1.35	1.26	0.81	90.18
2	2.31	92.82	0	2.31	0	1.55	0	1.01	0	92.82
3	0	0	90.39	2.38	1.38	0.99	2.88	0.99	0.99	90.39
4	0	1.23	2.84	90.55	1.42	1.42	1.31	1.23	0	90.55
5	0.63	1.13	0.75	1.26	92.22	0.63	1.44	0.81	1.13	92.22
6	1.01	1.09	1.28	1.56	1.19	92.86	0.55	0.46	0	92.86
7	0	1.12	0.51	0.61	2.09	0	93.58	1.07	1.02	93.58
8	0.47	1.42	0.95	1.33	2.18	1.90	0	91.09	0.66	91.09
9	1.14	0	2.06	2.01	0	2.09	0	2.15	90.55	90.55
Producer’s Accuracy	94.19	91.03	91.50	88.76	91.77	88.73	92.55	91.02	95.15
Kappa Coefficient: 0.913					Overall Accuracy: 91.61%

and

Table 4. The error matrix of classification for the Pavia City Center dataset (in percentage).

Classes	Reference Data									User’s Accuracy
	1	2	3	4	5	6	7	8	9
1	98.69	0.14	0.51	0.33	0.33	0	0	0	0	98.69
2	1.04	97.58	0.43	0	0	0.29	0.17	0.48	0	97.58
3	0.59	0.76	96.31	0.69	0.99	0	0	0	0.67	96.31
4	0	0.52	0.66	96.79	0.37	0.47	0.66	0.53	0	96.79
5	0	0	0.39	0.34	97.86	0.21	0.34	0.34	0.52	97.86
6	0.33	0.26	0.54	0	0	98.26	0	0.26	0.35	98.26
7	0.34	0.25	0	0.35	0	0.38	98.33	0.35	0	98.33
8	0	0	0.37	0.30	0.37	0.49	0.45	97.55	0.46	97.55
9	0.39	0.55	0.75	0.29	0.29	0	0	0	97.73	97.73
Producer’s Accuracy	97.34	97.52	96.34	97.67	97.65	98.16	98.38	98.03	97.99
Kappa Coefficient: 0.972					Overall Accuracy: 97.68%

. These four measures are briefly defined in the following. The user’s accuracy and the producer’s accuracy are two commonly applied measures for classification accuracy. The user’s accuracy is the ratio of the number of pixels classified correctly in each class by the amount of pixel in the same class. The user’s accuracy is a commission error, while the producer’s accuracy measures the errors of omission and expresses the probability that some samples of a given class on the ground are actually identified as such. The kappa coefficient, which is also termed the kappa statistic, is defined as a measure of the difference between the changed agreement and the actual agreement. The proposed MKFLE algorithm achieved overall accuracies of 83.58% in IPS-10, 91.61% in Pavia University, and 97.68% in Pavia City Center with 0.829, 0.913, and 0.972 in kappa coefficients, respectively.

Furthermore, the main difference of computational complexity between MKFLE and FKNFLE is the SVM. Although the computational complexity of SVM is $O\left(N^2\right)$, which means that while the number of training samples increases, the training process of MKFLE would be time-consuming. However, since the training process is offline, the testing process is unaffected, and as aforementioned that if there is not a good DR algorithm to find a suitable lower dimensional representation for the training data, the performance of deep learning algorithms would be seriously impacted. Therefore, the proposed MKFLE is still competitive.

5. Discussion

The proposed MKFLE dimension reduction algorithm was applied in HSI classification. Since the MKFLE algorithm applies the multiple kernel, which could extract much more useful nonlinear information, and accordingly obtained a better accuracy than that of FKNFLE to the value of 0.24%, 0.3%, and 0.09% for IPS-10, Pavia City Center, and Pavia University datasets, respectively. Although the improvements were few percentage, and increase the complexity of the algorithm. However, since the training process of MKFLE including the SVM process are offline, the testing process is unaffected. Besides, MKFLE is with lower variant OA rate. Therefore, the proposed MKFLE algorithm is suitable for dimension reduction.

6. Conclusions

In this study, a dimension reduction MKFLE algorithm based on general FLE transformation has been proposed and applied in HSI classification. The SVM-based multiple kernel learning strategy was considered to extract the multiple different non-linear manifold locality. The proposed MKFLE was compared with three previous state-of-the-art works, FKNFLE, KNFLE, and FNFLE. Three classic datasets, IPS-10, Pavia University, and Pavia City Center, were applied for evaluating the effectiveness of variant algorithms. Based on the experimental results, the proposed MKFLE had better performance than the other methods. More specifically, based on the 1-NN matching rule, the accuracy of MKFLE was better than that of FKNFLE to the value of 0.24%, 0.3%, and 0.09% for IPS-10, Pavia City Center, and Pavia University datasets, respectively. Moreover, the proposed MKFLE has higher accuracy and lower accuracy variant than FKNFLE. However, since SVM was applied in the training process of MKFLE, more training time than the FKNFLE was needed. Therefore, more efficient computational schemes for selecting the support vectors will be investigated in further research.