Estimation of Land Surface Heat Fluxes Based on Landsat 7 ETM+ Data and Field Measurements over the Northern Tibetan Plateau
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.1.1. Study Area
2.1.2. Ground-Based Data
2.1.3. Satellite Data
2.2. Method and Model
2.2.1. The Combinatory Method (CM)
2.2.2. The SEBS (Surface Energy Balance System) Model
3. Results
3.1. Comparison of SEBS and CM Results
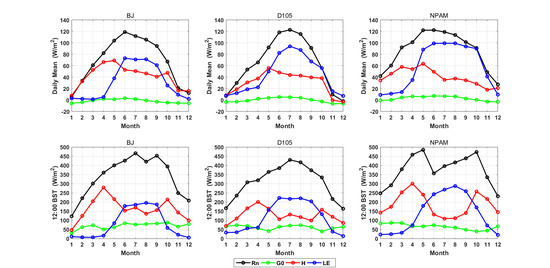
3.2. Multiple Timescale Variations in Land Surface Heat Fluxes
3.3. Spatial Distributions of Land Surface Heat Fluxes
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Foken. Micrometeorology, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 8–23. [Google Scholar]
- Ullah, S.; Tahir, A.A.; Akbar, T.A.; Hassan, Q.K.; Dewan, A.; Khan, A.J.; Khan, M. Remote sensing-based quantification of the relationships between land use land cover changes and surface temperature over the lower Himalayan region. Sustainability 2019, 11, 5492. [Google Scholar] [CrossRef] [Green Version]
- Kato, S.; Yamaguchi, Y. Analysis of urban heat-island effect using ASTER and ETM+ data: Separation of anthropogenic heat discharge and natural heat radiation from sensible heat flux. Remote Sens. Environ. 2005, 99, 44–54. [Google Scholar] [CrossRef]
- Chakraborty, S.D.; Kant, Y.; Mitra, D. Assessment of land surface temperature and heat fluxes over Delhi using remote sensing data. J. Environ. Manag. 2015, 148, 143–152. [Google Scholar] [CrossRef]
- Ma, Y.; Tian, H.; Ishikawa, H.; Ohba, R.; Ueda, H.; Wen, J. Determination of regional land surface heat fluxes over a heterogeneous landscape of the Jiddah area of Saudi Arabia by using Landsat-7 ETM data. Hydrol. Process. 2006, 21, 1892–1900. [Google Scholar] [CrossRef]
- Zahira, S.; Abderrahmane, H.; Mederbal, K.; Frederic, D. Mapping latent heat flux in the western forest covered regions of Algeria using remote sensing data and a spatialized model. Remote Sens. 2009, 1, 795–817. [Google Scholar] [CrossRef] [Green Version]
- Carrasco-Benavides, M.; Ortega-Farías, S.; Lagos, L.O.; Kleissl, J.; Morales-Salinas, L.; Kilic, A. Parameterization of the satellite-based model (METRIC) for the estimation of instantaneous surface energy balance components over a drip-irrigated vineyard. Remote Sens. 2014, 6, 11342–11371. [Google Scholar] [CrossRef] [Green Version]
- Teixeira, A.H.C.; Padovani, C.R.; Andrade, R.G.; Leivas, J.F.; Victoria, D.D.C.; Galdino, S. Use of MODIS images to quantify the radiation and energy balances in the Brazilian Pantanal. Remote Sens. 2015, 7, 14597–14619. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Qiu, J.; Su, H.; Bai, Q.; Liu, S.; Li, L.; Yu, Y.; Huang, Y. A one-source approach for estimating land surface heat fluxes using remotely sensed land surface temperature. Remote Sens. 2017, 9, 43. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Su, Z.; Li, Z.; Koike, T.; Menenti, M. Determination of regional net radiation and soil heat flux over a heterogeneous landscape of the Tibetan Plateau. Hydrol. Process. 2002, 16, 2963–2971. [Google Scholar] [CrossRef]
- Ma, Y.; Zhong, L.; Su, Z.; Ishikawa, H.; Menenti, M.; Koike, T. Determination of regional distributions and seasonal variations of land surface heat fluxes from Landsat-7 Enhanced Thematic Mapper data over the central Tibetan Plateau area. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Oku, Y.; Ishikawa, H.; Su, Z. Estimation of land surface heat fluxes over the Tibetan Plateau using GMS data. J. Appl. Meteorol. Climatol. 2007, 46, 183–195. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Ma, Y.; Li, M.; Hu, Z.; Zhong, L.; Su, Z.; Ishikawa, H.; Wang, J. Estimating surface fluxes over the north Tibetan Plateau area with ASTER imagery. Hydrol. Earth Syst. Sci. 2009, 13, 57–67. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Zhong, L.; Wang, B.; Ma, W.; Chen, X.; Li, M. Determination of land surface heat fluxes over heterogeneous landscape of the Tibetan Plateau by using the MODIS and in situ data. Atmos. Chem. Phys. 2011, 11, 10461–10469. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Su, Z.; Ma, Y.; Yang, K.; Wang, B. Estimation of surface energy fluxes under complex terrain of Mt. Qomolangma over the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2013, 17, 1607–1618. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Han, C.; Zhong, L.; Wang, B.; Zhu, Z.; Wang, Y.; Zhang, L.; Meng, C.; Xu, C.; Amatya, P. Using MODIS and AVHRR data to determine regional surface heating field and heat flux distributions over the heterogeneous landscape of the Tibetan Plateau. Theor. Appl. Climatol. 2014, 117, 643–652. [Google Scholar] [CrossRef] [Green Version]
- Han, C.; Ma, Y.; Chen, X.; Su, Z. Estimates of land surface heat fluxes of the Mt. Everest region over the Tibetan Plateau utilizing ASTER data. Atmos. Res. 2016, 168, 180–190. [Google Scholar] [CrossRef]
- Zhong, L.; Ma, Y.; Hu, Z.; Fu, Y.; Hu, Y.; Wang, X.; Cheng, M.; Ge, N. Estimation of hourly land surface heat fluxes over the Tibetan Plateau by the combined use of geostationary and polar-orbiting satellites. Atmos. Chem. Phys. 2019, 19, 5529–5541. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Yang, K. China Meteorological Forcing Dataset; Cold and Arid Regions Science Data Center: Lanzhou, China, 2011. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Yang, K.; He, J.; Qin, J.; Shi, J.C.; Du, J.Y.; He, Q. Improving land surface temperature modeling for dry land of China. J. Geophys. Res. 2011, 116, D20104. [Google Scholar] [CrossRef]
- Ma, Y.; Su, Z.; Koike, T.; Yao, T.; Ishikawa, H.; Ueno, K.; Menenti, M. On measuring and remote sensing surface energy partitioning over the Tibetan Plateau—From GAME/Tibet to CAMP/Tibet. Phys. Chem. Earth 2003, 28, 63–74. [Google Scholar] [CrossRef]
- Thom, A.S.; Stewart, J.B.; Oliver, H.R.; Gash, J.H.C. Comparison of aerodynamic and energy budget estimates of fluxes over a pine forest. Q. J. R. Meteorol. Soc. 1975, 101, 93–105. [Google Scholar] [CrossRef]
- Hu, Y.; Qi, Y. The combinatory method for determination of the turbulent fluxes and universal functions in the surface layer. J. Meteorol. Res. 1993, 7, 101–109. [Google Scholar]
- Zou, M.; Zhong, L.; Ma, Y.; Hu, Y.; Feng, L. Estimation of actual evapotranspiration in the Nagqu river basin of the Tibetan Plateau. Theor. Appl. Climatol. 2018, 132, 1039–1047. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Foken, T. 50 years of the Monin-Obukhov Similarity Theory. Bound. Layer Meteorol. 2006, 119, 431–447. [Google Scholar] [CrossRef]
- Brutsaert, W. On a derivable formula for long-wave radiation from clear skies. Water Resour. Res. 1975, 11, 742–744. [Google Scholar] [CrossRef]
- Kumar, L.; Skidmore, A.K.; Knowles, E. Modelling topographic variation in solar radiation in a GIS environment. Int. J. Geogr. Inf. Sci. 1997, 11, 475–497. [Google Scholar] [CrossRef]
- Yang, K.; He, J.; Tang, W.J.; Qin, J.; Cheng, C.C.K. On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- Dhungel, R.; Allen, R.G.; Trezza, R.; Robison, C.W. Comparison of latent heat flux using aerodynamic methods and using the Penman-Monteith method with satellite-based surface energy balance. Remote Sens. 2014, 6, 8844–8877. [Google Scholar] [CrossRef] [Green Version]
- Daughtry, C.S.T.; Kustas, W.P.; Moran, M.S.; Pinter, P.J., Jr.; Jackson, R.D.; Brown, P.W.; Nichols, W.D.; Gay, L.W. Spectral estimates of net radiation and soil heat flux. Remote Sens. Environ. 1990, 32, 111–124. [Google Scholar] [CrossRef]
- Gao, Z.Q.; Liu, C.S.; Gao, W.; Chang, N.B. A coupled remote sensing and the Surface Energy Balance with Topography Algorithm (SEBTA) to estimate actual evapotranspiration over heterogeneous terrain. Hydrol. Earth Syst. Sci. 2011, 15, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Brutsaert, W. Aspects of bulk atmospheric boundary layer similarity under free-convective conditions. Rev. Geophys. 1999, 37, 439–451. [Google Scholar] [CrossRef]
- Yang, K.; Koike, T.; Fujii, H.; Tamagawa, K.; Hirose, N. Improvement of surface flux parametrizations with a turbulence-related length. Q. J. R. Meteorol. Soc. 2002, 128, 2073–2087. [Google Scholar] [CrossRef]
- Faivre, R.; Colin, J.; Menenti, M. Evaluation of methods for aerodynamic roughness length retrieval from very high-resolution imaging LIDAR observations over the Heihe basin in China. Remote Sens. 2017, 9, 63. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Wang, Y.; Wu, R.; Hu, Z.; Yang, K.; Li, M.; Ma, W.; Zhong, L.; Sun, F.; Chen, X.; et al. Recent advances on the study of atmosphere-land interaction observations on the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2009, 13, 1103–1111. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Fan, S.; Ishikawa, H.; Tsukamoto, O.; Yao, T.; Koike, T.; Zuo, H.; Hu, Z.; Su, Z. Diurnal and inter-monthly variation of land surface heat fluxes over the central Tibetan Plateau area. Theor. Appl. Climatol. 2005, 80, 259–273. [Google Scholar] [CrossRef]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef]
- Zhong, L.; Ma, Y.; Su, Z.; Lu, L.; Ma, W.; Lu, Y. Land-atmosphere energy transfer and surface boundary layer characteristics in the Rongbu Valley on the northern slope of Mt. Everest. Arct. Antarct. Alp. Res. 2009, 41, 396–405. [Google Scholar] [CrossRef] [Green Version]
- Leuning, R.; Gorsel, E.V.; Massman, W.J.; Isaac, P.R. Reflections on the surface energy imbalance problem. Agric. For. Meteorol. 2012, 156, 65–74. [Google Scholar] [CrossRef]
- Sousa, D.; Small, C. Spectral Mixture Analysis as a unified framework for the remote sensing of evapotranspiration. Remote Sens. 2018, 10, 1961. [Google Scholar] [CrossRef] [Green Version]
- Zou, M.; Zhong, L.; Ma, Y.; Hu, Y.; Huang, Z.; Xu, K.; Feng, L. Comparison of two satellite-based evapotranspiration models of the Nagqu River Basin of the Tibetan Plateau. J. Geophys. Res. Atmos. 2018, 123, 3961–3975. [Google Scholar] [CrossRef]





| Station | Longitude (°E) | Latitude (°N) | Altitude (m) | Underlying Land Cover Type |
|---|---|---|---|---|
| ANNI | 92.17244 | 31.25442 | 4480 | Alpine and subalpine meadow |
| BJ | 91.89871 | 31.36866 | 4509 | Alpine and subalpine meadow |
| D105 | 91.94256 | 33.06429 | 5039 | Alpine and subalpine plain grass |
| NPAM | 91.71468 | 31.92623 | 4620 | Alpine and subalpine meadow |
| Meteorological Elements | Levels | Level Heights | Temporal Resolution | Accuracy | Instruments |
|---|---|---|---|---|---|
| Wind speed | 3 | z = 10 m, 5 m, 1 m | 1 h | 0.1 m/s | WS-D32 (Komatsu) |
| Air temperature | 2 | z = 8.2 m, 1 m | 1 h | 0.05 K | TS-801/Pt100 (Okazaki) |
| Air pressure | 1 | z = 0.5 m | 1 h | 0.5 hPa | PTB220C (Vaisala) |
| Relative humidity | 2 | z = 8.2 m, 1 m | 1 h | 2% | HMP-45D (Vaisala) |
| Radiation budgets | 1 | z = 1.28 m | 1 h | 5% | CM21 (Kipp&Zonen) (for shortwave), PIR (Kipp&Zonen) (for longwave) |
| Soil temperature | 6 | z = 0 cm, 0 cm, −4 cm, −10 cm, −20 cm, −40 cm | 1 h | 0.2 K | TS-301/Pt100 (Okazaki) |
| Soil heat flux | 2 | z = −10 cm, −20 cm | 1 h | 2% | MF-81 (EKO) |
| Scene | Path/Row | Date (dd/mm/yyyy) | Overpass Time |
|---|---|---|---|
| 1 | 137/038 | 13/11/2001 | 04:11 UTC |
| 2 | 137/038 | 16/11/2002 | 04:10 UTC |
| 3 | 137/038 | 03/01/2003 | 04:11 UTC |
| 4 | 137/038 | 04/02/2003 | 04:11 UTC |
| 5 | 137/038 | 24/03/2003 | 04:11 UTC |
| 6 | 138/037 | 13/06/2001 | 04:18 UTC |
| 7 | 138/037 | 15/05/2002 | 04:17 UTC |
| 8 | 138/038 | 13/06/2001 | 04:18 UTC |
| 9 | 138/038 | 04/11/2001 | 04:17 UTC |
| 10 | 138/038 | 06/12/2001 | 04:17 UTC |
| 11 | 138/038 | 15/05/2002 | 04:17 UTC |
| 12 | 138/038 | 22/10/2002 | 04:16 UTC |
| 13 | 138/038 | 16/04/2003 | 04:17 UTC |
| Channel | Band | Wavelength Range (μm) | Spatial Resolution (m) |
|---|---|---|---|
| 1 | Blue | 0.45–0.52 | 30 |
| 2 | Green | 0.52–0.60 | 30 |
| 3 | Red | 0.63–0.69 | 30 |
| 4 | Near infrared | 0.76–0.90 | 30 |
| 5 | Shortwave infrared | 1.55–1.75 | 30 |
| 6 | Thermal infrared | 10.4–12.5 | 60 |
| 7 | Shortwave infrared | 2.08–2.35 | 30 |
| 8 | Panchromatic | 0.5–0.9 | 15 |
| Date | 13/06/2001 | 04/11/2001 | 06/12/2001 | 15/05/2002 | Mean | |
|---|---|---|---|---|---|---|
| Net radiation flux | Q1 | 566.4 | 357.8 | 271.5 | 514.8 | 427.6 |
| Q2 | 631.8 | 404.4 | 314.3 | 583.0 | 483.4 | |
| Q3 | 704.2 | 451.6 | 359.4 | 668.5 | 545.9 | |
| Soil heat flux | Q1 | 36.7 | 22.9 | 17.6 | 33.5 | 27.7 |
| Q2 | 40.9 | 26.1 | 20.5 | 37.9 | 31.3 | |
| Q3 | 45.7 | 29.4 | 23.6 | 43.5 | 35.5 | |
| Sensible heat flux | Q1 | 176.4 | 130.3 | 147.6 | 161.6 | 154.0 |
| Q2 | 252.7 | 221.4 | 204.8 | 219.5 | 224.6 | |
| Q3 | 341.9 | 302.8 | 257.4 | 289.9 | 298.0 | |
| Latent heat flux | Q1 | 195.2 | 61.3 | 2.8 | 204.3 | 115.9 |
| Q2 | 320.1 | 142.3 | 75.5 | 298.3 | 209.1 | |
| Q3 | 443.7 | 223.2 | 139.1 | 413.9 | 305.0 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, N.; Zhong, L.; Ma, Y.; Cheng, M.; Wang, X.; Zou, M.; Huang, Z. Estimation of Land Surface Heat Fluxes Based on Landsat 7 ETM+ Data and Field Measurements over the Northern Tibetan Plateau. Remote Sens. 2019, 11, 2899. https://doi.org/10.3390/rs11242899
Ge N, Zhong L, Ma Y, Cheng M, Wang X, Zou M, Huang Z. Estimation of Land Surface Heat Fluxes Based on Landsat 7 ETM+ Data and Field Measurements over the Northern Tibetan Plateau. Remote Sensing. 2019; 11(24):2899. https://doi.org/10.3390/rs11242899
Chicago/Turabian StyleGe, Nan, Lei Zhong, Yaoming Ma, Meilin Cheng, Xian Wang, Mijun Zou, and Ziyu Huang. 2019. "Estimation of Land Surface Heat Fluxes Based on Landsat 7 ETM+ Data and Field Measurements over the Northern Tibetan Plateau" Remote Sensing 11, no. 24: 2899. https://doi.org/10.3390/rs11242899
APA StyleGe, N., Zhong, L., Ma, Y., Cheng, M., Wang, X., Zou, M., & Huang, Z. (2019). Estimation of Land Surface Heat Fluxes Based on Landsat 7 ETM+ Data and Field Measurements over the Northern Tibetan Plateau. Remote Sensing, 11(24), 2899. https://doi.org/10.3390/rs11242899