Active Semi-Supervised Random Forest for Hyperspectral Image Classification
Abstract
:1. Introduction
- (1)
- A new query function considering spectral-spatial information, termed DUSSC, is proposed for active learning.
- (2)
- Supervised clustering algorithm is used to mine the structure of the data and divide the data for active learning and pseudolabeling.
- (3)
- We assign pseudolabels to some unlabeled samples to avoid the bias caused by AL-labeled samples.
- (4)
- A unified framework embedding AL and SSL into random forest is proposed for HSI classification.
2. Related Work
2.1. Semi-Supervised Random Forest
2.2. Active Learning
2.3. Clustering Methods in HSI Classification
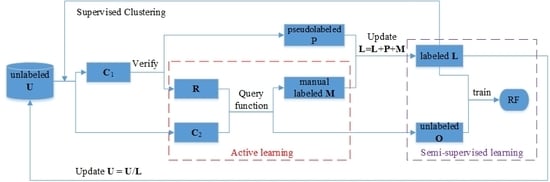
3. Proposed ASSRF Method
3.1. Proposed Query Function for Active Learning
3.2. Supervised K-Means Clustering
| Algorithm 1 Supervised k-means clustering |
| Input: data set D containing labeled pixels L and unlabeled pixels U 1: Divide D into k clusters through k-means, where k represents class number of labeled pixels L; 2: Repeat 3: Count the labeled pixels in each cluster; 4: If the labeled pixels in each cluster do not all belong to the same category, then 5: Divide the impure cluster into k clusters through k-means algorithm, where k represents class number of the labeled pixels in this cluster; 6: End if 7: Generate a set of clusters; 8: Until the labeled pixels in each cluster have the same class label or the cluster doesn’t have labeled pixels. Output: the pure clusters. |
3.3. Details of ASSRF Classification
- (1)
- Set the pseudolabeled data P and manually labeled data M as empty. Initial labeled data is set to L, train the random forest RF on the initial labeled data L.
- (2)
- Use Algorithm 1 to divide the unlabeled data U into many pure clusters.
- (3)
- The clusters that contain labeled samples are merged into set C1, and the clusters that do not contain labeled samples are merged into set C2.
- (4)
- Train a temporary random forest rfm on labeled data L.
- (5)
- The samples in set C1 are classified by rfm, and g samples with high classification confidence are assigned with pseudolabels. Let g samples form a set P, and let R = C1/P.
- (6)
- Let the candidate pool S = C2 ∪ R.
- (7)
- Use the query function DUSSC to select h samples from set S for manual labeling. Let h manually labeled samples form a set M.
- (8)
- Let O = S/M, and update L: L = L ∪ P ∪ M.
- (9)
- Use random forest RF to classify the samples in O and obtain the probability that each sample belongs to each class.
- (10)
- Compute the margin vector of each sample in O by using Equation (3).
- (11)
- Calculate the probability distribution of each sample in O by using Equation (8), and we assign a random class label to each sample by using the probability distribution.
- (12)
- Use data L and O to retrain each tree in RF.
- (13)
- Update the unlabeled data U: U = U/L.
- (14)
- Repeat the steps 2 to 13 multiple times to obtain the final random forest RF.
| Algorithm 2 Active semi-supervised random forest classification |
| Input: a training data set D containing labeled pixels L and unlabeled pixels U, the size of the forest N, the batch size h for active learning, the batch size of the pseudolabeled samples g, an initial temperature T0 and a cooling function c(T, m). Initialization: the manually labeled data M = Ø and the pseudolabeled data P = Ø. 1: Train the random forest: RF ⟵ trainRF(L). 2: Set epoch: m = 0. 3: Repeat 4: Obtain the current temperature Tm+1 ⟵ c(T, m); 5: Set m ⟵ m+1; 6: Divide data U into C1 and C2 based on Algorithm 1; 7: Train temporary random forest rfm: rfm ⟵ trainRF(L); 8: Classify the samples in C1 by using rfm; 9: Select g samples with the highest-class probabilities from C1, and give them pseudolabels. Let g samples form a set P, and R = C1/P; 10: Query h most informative samples (M) from S (S = C2 ∪ R) by SSCDU for manual labeling; 11: Let O = S/M and update L = L ∪ P ∪ M; 12: ∀ x∈O, obtain the class probability p(i|x) by using RF to classify each sample x; 13: ∀ x∈O, compute the margin by using Equation (3); 14: ∀ x∈O, k∈Y: compute p*(k|x) by using Equation (8); 15: For n =1 to N do 16: ∀ x∈O: Assign a random label y’ from the p*(k|x) distribution. 17: Set Xn = L ∪ {(x, y’)|x∈O}; 18: Retrain the tree: fn ⟵ trainTree(Xn); 19: End for 20: Update U = U/L; 21: Until epoch rounds are reached; 22: Output: the forest RF. |
4. Experimental Results and Analysis
4.1. Hyperspectral Image Data Sets
- (1)
- The Kennedy Space Center (KSC) data was acquired by the NASA Airborne Visible Infrared Imaging Spectrometer sensor over the KSC, Florida, on 23 March 1996. The original data has 224 spectral bands. We used only 176 bands for our experiments because water absorption bands and bands with low signal-to-noises were excluded. The data set contained 13 classes with a size of 512 pixels × 614 pixels and the spatial resolution was 18 m/pixel. There were a total of 5211 labeled pixels in the data set.
- (2)
- The Pavia University (PaviaU) data was obtained by the Reflective Optics Spectrographic Imaging System over an urban scene by Pavia University, Italy, in 2001. There were 115 spectral bands with wavelengths ranging from 0.43 to 0.86 μm. We chose 103 bands for the experiments after removing 12 noisy and water absorption bands. This data set had a size of 610 pixels × 340 pixels with a spatial resolution of 1.3 m/pixel. A total of 42,776 pixels covering nine classes were labeled.
- (3)
- The Botswana (BOT) data was obtained by the NASA Earth Observing-1 satellite over the Okavango Delta, Botswana, on 11 May 2001. The original data has 242 bands. After removing uncalibrated and noisy bands, the remaining 145 bands were used in the experiments. The BOT data set was 1476 pixels × 256 pixels in size and had a spatial resolution of 30 m/pixel. There were 3248 labeled pixels covering 14 classes in total.
4.2. Experimental Setup
4.3. Comparison with RF and SSRF
4.4. Comparison with Other State-Of-The-Art Methods
4.5. Parameter Sensitivity Analysis
4.6. Further Analysis of ASSRF
5. Discussion
- As shown in Section 4.3 and Section 4.4, compared with other methods, ASSRF performed better classification performance. The good performance of ASSRF could be attributed to the following three reasons. First, supervised clustering can extract the structure of the whole data and divide it into two parts, one for active learning and one for pseudolabeling. Second, the proposed query function DUSSC can select the most informative and diverse samples for manual labeling. Third, the unified framework combining AL and SSL can increase the learning performance by increasing the quantity and quality of the labeled samples.
- The results from Table 8 show that the computation time of ASSRF was acceptable. Several reasons could explain this result. First, the training process of each tree in the forest was parallel. Second, the time complexity of k-means algorithm was linear, and the time cost of supervised k-means method was at most m times the k-means, where m is the number of labeled samples. Third, the process of DA-based SSL could be solved as an analytical solution, which made the computation of SSL is on line.
- The parameter analysis in Section 4.5 shows that ASSRF was robust to parameters. According to our experiments, the recommended value for α ranges from 0.1 to 0.25 and the recommended value for β ranges from 0.35 to 0.55.
- The experimental results from Section 4.6 show that both the spectral-spatial constraint and supervised k-means clustering algorithm played an important role in ASSRF. This is mainly because that ASSRF without supervised clustering does not provide enough pseudolabeled samples for the classification model. In other words, the model focuses on informative samples but ignores the samples easy, which are to classify, leading to the bias of the model and affecting the final accuracy. Another finding was that the importance of spectral-spatial constraint was less than supervised clustering.
- ASSRF is a unified framework combing AL and SSL into random forest. Generally, ASSRF can be used for any data represented in vector form. However, we added spectral-spatial constraints into query function for AL, where the spectral-spatial constraint utilized the neighborhood structure information of images. So, for usual data represented in vector form, the entropy-only-based ASSRF was appropriate.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zare, A.; Bolton, J.; Gader, P.; Schatten, M. Vegetation mapping for landmine detection using long-wave hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2008, 46, 172–178. [Google Scholar] [CrossRef]
- Fu, Y.; Zhao, C.; Wang, J.; Jia, X.; Yang, G.; Song, X.; Feng, H. An improved combination of spectral and spatial features for vegetation classification in hyperspectral images. Remote Sens. 2017, 9, 261. [Google Scholar] [CrossRef] [Green Version]
- Jiao, L.; Sun, W.; Yang, G.; Ren, G.; Liu, Y. A hierarchical classification framework of satellite multispectral/hyperspectral images for mapping coastal wetlands. Remote Sens. 2019, 11, 2238. [Google Scholar] [CrossRef] [Green Version]
- Moeini Rad, A.; Abkar, A.A.; Mojaradi, B. Supervised distance-based feature selection for hyperspectral target detection. Remote Sens. 2019, 11, 2049. [Google Scholar] [CrossRef] [Green Version]
- Wei, L.; Huang, C.; Zhong, Y.; Wang, Z.; Hu, X.; Lin, L. Inland waters suspended solids concentration retrieval based on PSO-LSSVM for UAV-borne hyperspectral remote sensing imagery. Remote Sens. 2019, 11, 1455. [Google Scholar] [CrossRef] [Green Version]
- Patra, S.; Bruzzone, L. A novel SOM-SVM-based active learning technique for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6899–6910. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef] [Green Version]
- Seydgar, M.; Alizadeh Naeini, A.; Zhang, M.; Li, W.; Satari, M. 3-D convolution-recurrent networks for spectral-spatial classification of hyperspectral images. Remote Sens. 2019, 11, 883. [Google Scholar] [CrossRef] [Green Version]
- Belgiu, M.; Drăgu, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, G.; Li, X.; Wang, B. Cascaded random forest for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1082–1094. [Google Scholar] [CrossRef]
- Xia, J.; Ghamisi, P.; Yokoya, N.; Iwasaki, A. Random forest ensembles and extended multiextinction profiles for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 202–216. [Google Scholar] [CrossRef] [Green Version]
- Rajan, S.; Ghosh, J.; Crawford, M.M. An active learning approach to hyperspectral data classification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1231–1242. [Google Scholar] [CrossRef]
- Kong, Y.; Wang, X.; Cheng, Y.; Chen, C.L.P. Hyperspectral imagery classification based on semi-supervised broad learning system. Remote Sens. 2018, 10, 685. [Google Scholar] [CrossRef] [Green Version]
- Crawford, M.M.; Tuia, D.; Yang, H.L. Active learning: Any value for classification of remotely sensed data? Proc. IEEE 2013, 101, 593–608. [Google Scholar] [CrossRef] [Green Version]
- Tuia, D.; Volpi, M.; Copa, L.; Kanevski, M.; Muñoz-Marí, J. A survey of active learning algorithms for supervised remote sensing image classification. IEEE J. Sel. Top. Signal Process. 2011, 5, 606–617. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Motagh, M. Random forest wetland classification using ALOS-2 L-band, RADARSAT-2 C-band, and TerraSAR-X imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 13–31. [Google Scholar] [CrossRef]
- Chan, J.C.W.; Paelinckx, D. Evaluation of random forest and Adaboost tree-based ensemble classification and spectral band selection for ecotope mapping using airborne hyperspectral imagery. Remote Sens. Environ. 2008, 112, 2999–3011. [Google Scholar] [CrossRef]
- Ghimire, B.; Rogan, J.; Miller, J. Contextual land-cover classification: Incorporating spatial dependence in land-cover classification models using random forests and the Getis statistic. Remote Sens. Lett. 2010, 1, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Ham, J.S.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef] [Green Version]
- Mellor, A.; Boukir, S.; Haywood, A.; Jones, S. Exploring issues of training data imbalance and mislabelling on random forest performance for large area land cover classification using the ensemble margin. ISPRS J. Photogramm. Remote Sens. 2015, 105, 155–168. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Xia, J.; Liao, W.; Chanussot, J.; Du, P.; Song, G.; Philips, W. Improving random forest with ensemble of features and semisupervised feature extraction. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1471–1475. [Google Scholar]
- Behnamian, A.; Millard, K.; Banks, S.N.; White, L.; Richardson, M.; Pasher, J. A systematic approach for variable selection with random rorests: Achieving stable variable importance values. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1988–1992. [Google Scholar] [CrossRef] [Green Version]
- Romaszewski, M.; Głomb, P.; Cholewa, M. Semi-supervised hyperspectral classification from a small number of training samples using a co-training approach. ISPRS J. Photogramm. Remote Sens. 2016, 121, 60–76. [Google Scholar] [CrossRef]
- Zhang, X.; Song, Q.; Liu, R.; Wang, W.; Jiao, L. Modified co-training with spectral and spatial views for semisupervised hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2044–2055. [Google Scholar] [CrossRef]
- Dopido, I.; Li, J.; Marpu, P.R.; Plaza, A.; Bioucas Dias, J.M.; Benediktsson, J.A. Semisupervised self-learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4032–4044. [Google Scholar] [CrossRef] [Green Version]
- Mianji, F.A.; Gu, Y.; Zhang, Y.; Zhang, J. Enhanced self-training superresolution mapping technique for hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2011, 8, 671–675. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Bandos Marsheva, T.V.; Zhou, D. Semi-supervised graph-based hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3044–3054. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, G.; Shafique, A.; Fu, P. Label propagation ensemble for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3623–3636. [Google Scholar] [CrossRef]
- Gómez-Chova, L.; Camps-Valls, G.; Muñoz-Mari, J.; Calpe, J. Semisupervised image classification with Laplacian support vector machines. IEEE Geosci. Remote Sens. Lett. 2008, 5, 336–340. [Google Scholar] [CrossRef]
- Yang, L.; Yang, S.; Jin, P.; Zhang, R. Semi-supervised hyperspectral image classification using spatio-spectral laplacian support vector machine. IEEE Geosci. Remote Sens. Lett. 2013, 11, 651–655. [Google Scholar] [CrossRef]
- Tomašev, N.; Buza, K. Hubness-aware kNN classification of high-dimensional data in presence of label noise. Neurocomputing 2015, 160, 157–172. [Google Scholar] [CrossRef] [Green Version]
- Buza, K. Classification of gene expression data: A hubness-aware semi-supervised approach. Comput. Methods Programs Biomed. 2016, 127, 105–113. [Google Scholar] [CrossRef] [Green Version]
- Marussy, K.; Buza, K. SUCCESS: A new approach for semi-supervised classification of time-series. In Proceedings of the International Conference on Artificial Intelligence and Soft Computing, Zakopane, Poland, 9–13 June 2013; Springer: Berlin, Germany; pp. 437–447. [Google Scholar]
- Peikari, M.; Salama, S.; Nofech-Mozes, S.; Martel, A.L. A Cluster-then-label semi-supervised learning approach for pathology image classification. Sci. Rep. 2018, 8, 7193. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Semisupervised hyperspectral image segmentation using multinomial logistic regression with active learning. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4085–4098. [Google Scholar] [CrossRef] [Green Version]
- Munoz-Mari, J.; Tuia, D.; Camps-Valls, G. Semisupervised classification of remote sensing images with active queries. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3751–3763. [Google Scholar] [CrossRef]
- Samiappan, S.; Moorhead, R.J. Semi-supervised co-training and active learning framework for hyperspectral image classification. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 401–404. [Google Scholar]
- Di, W.; Crawford, M.M. Active learning via multi-view and local proximity co-regularization for hyperspectral image classification. IEEE J. Sel. Top. Signal Process. 2011, 5, 618–628. [Google Scholar] [CrossRef] [Green Version]
- Wan, L.; Tang, K.; Li, M.; Zhong, Y.; Qin, A.K. Collaborative active and semisupervised learning for hyperspectral remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2384–2396. [Google Scholar] [CrossRef]
- Wang, Z.; Du, B.; Zhang, L.; Zhang, L.; Jia, X. A novel semisupervised active-learning algorithm for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3071–3083. [Google Scholar] [CrossRef]
- Zhang, Z.; Pasolli, E.; Crawford, M.M.; Tilton, J.C. An active learning framework for hyperspectral image classification using hierarchical segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 640–654. [Google Scholar] [CrossRef]
- Dopido, I.; Li, J.; Plaza, A.; Bioucas-Dias, J.M. Semi-supervised active learning for urban hyperspectral image classification. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 1586–1589. [Google Scholar]
- Leistner, C.; Saffari, A.; Santner, J.; Bischof, H. Semi-supervised random forests. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Kyoto, Japan, 27 September–4 October 2009; pp. 506–513. [Google Scholar]
- Amini, S.; Homayouni, S.; Safari, A. Semi-supervised classification of hyperspectral image using random forest algorithm. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Quebec, Canada, 13–18 July 2014; pp. 2866–2869. [Google Scholar]
- Demir, B.; Persello, C.; Bruzzone, L. Batch-mode active-learning methods for the interactive classification of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1014–1031. [Google Scholar] [CrossRef] [Green Version]
- Lewis, D.D.; Gale, W.A. A sequential algorithm for training text classifiers. In Proceedings of the 17th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Dublin, Ireland, 3–6 July 1994; pp. 3–12. [Google Scholar]
- Campbell, C.; Cristianini, N.; Smola, A. Query learning with large margin classifiers. In Proceedings of the 7th International Conference on Machine Learning (ICML), Stanford, CA, USA, 29 June–2 July 2000; pp. 111–118. [Google Scholar]
- Tong, S.; Koller, D. Support vector machine active learning with applications to text classification. J. Mach. Learn. Res. 2001, 2, 45–66. [Google Scholar]
- Di, W.; Crawford, M.M. View generation for multiview maximum disagreement based active learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1942–1954. [Google Scholar] [CrossRef]
- Freund, Y.; Seung, H.S.; Shamir, E.; Tishby, N. Selective sampling using the query by committee algorithm. Mach. Learn. 1997, 28, 133–168. [Google Scholar] [CrossRef]
- Tuia, D.; Ratle, F.; Pacifici, F.; Kanevski, M.F.; Emery, W.J. Active learning methods for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2218–2232. [Google Scholar] [CrossRef]
- Zhang, Z.; Crawford, M.M. A batch-mode regularized multimetric active learning framework for classification of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6594–6609. [Google Scholar] [CrossRef]
- Shi, Q.; Du, B.; Zhang, L. Spatial coherence-based batch-mode active learning for remote sensing image classification. IEEE Trans. Image Process. 2015, 24, 2037–2050. [Google Scholar]
- Demir, B.; Minello, L.; Bruzzone, L. An effective strategy to reduce the labeling cost in the definition of training sets by active learning. IEEE Geosci. Remote Sens. Lett. 2014, 11, 79–83. [Google Scholar] [CrossRef]
- Xue, Z.; Zhou, S.; Zhao, P. Active learning improved by neighborhoods and superpixels for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2018, 15, 469–473. [Google Scholar] [CrossRef]
- Pasolli, E.; Melgani, F.; Tuia, D.; Pacifici, F.; Emery, W.J. SVM active learning approach for image classification using spatial information. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2217–2223. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, X.; Li, J.; Plaza, A.; Prasad, S. Superpixel-based active learning and online feature importance learning for hyperspectral image analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 347–359. [Google Scholar] [CrossRef]
- Patra, S.; Bhardwaj, K.; Bruzzone, L. A spectral-spatial multicriteria active learning technique for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5213–5227. [Google Scholar] [CrossRef]
- Patra, S.; Bruzzone, L. A fast cluster-assumption based active-learning technique for classification of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1617–1626. [Google Scholar] [CrossRef]
- Volpi, M.; Tuia, D.; Kanevski, M. Memory-based cluster sampling for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3096–3106. [Google Scholar] [CrossRef]
- Tuia, D.; Muñoz-Marí, J.; Camps-Valls, G. Remote sensing image segmentation by active queries. Pattern Recognit. 2012, 45, 2180–2192. [Google Scholar] [CrossRef]
- Gaddam, S.R.; Phoha, V.V.; Balagani, K.S. K-Means+ID3: A novel method for supervised anomaly detection by cascading k-Means clustering and ID3 decision tree learning methods. IEEE Trans. Knowl. Data Eng. 2007, 19, 345–354. [Google Scholar] [CrossRef]
- Michel, V.; Gramfort, A.; Varoquaux, G.; Eger, E.; Keribin, C.; Thirion, B. A supervised clustering approach for fMRI-based inference of brain states. Pattern Recognit. 2012, 45, 2041–2049. [Google Scholar] [CrossRef] [Green Version]
- Ding, W.; Stepinski, T.F.; Parmar, R.; Jiang, D.; Eick, C.F. Discovery of feature-based hot spots using supervised clustering. Comput. Geosci. 2009, 35, 1508–1516. [Google Scholar] [CrossRef]
- Persello, C.; Bruzzone, L. Active and semisupervised learning for the classification of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6937–6956. [Google Scholar] [CrossRef]
- Chang, C.I. An information-theoretic approach to spectral variability, similarity, and discrimination for hyperspectral image analysis. IEEE Trans. Inf. Theory 2000, 46, 1927–1932. [Google Scholar] [CrossRef] [Green Version]
- Van der Meer, F. The effectiveness of spectral similarity measures for the analysis of hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 3–17. [Google Scholar] [CrossRef]
- Rodríguez, J.J.; Kuncheva, L.I.; Alonso, C.J. Rotation forest: A new classifier ensemble method. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1619–1630. [Google Scholar] [CrossRef]










| Class No. | Kennedy Space Center (KSC) | Pavia University (PaviaU) | Botswana (BOT) | |||
|---|---|---|---|---|---|---|
| Class Name | #Pixels | Class Name | #Pixels | Class Name | #Pixels | |
| 1 | Scrub | 761 | Asphalt | 6631 | Water | 270 |
| 2 | Willow | 243 | Meadows | 18,649 | Hippo grass | 101 |
| 3 | CP hammock | 256 | Gravel | 2099 | Floodplain grass1 | 251 |
| 4 | CP/Oak | 252 | Trees | 3064 | Floodplain grass2 | 215 |
| 5 | Slash pine | 161 | Metal Sheets | 1345 | Reeds1 | 269 |
| 6 | Oak/Broadleaf | 229 | Bare Soil | 5029 | Riparian | 269 |
| 7 | Hardwood swamp | 105 | Bitumen | 1330 | Firescar2 | 259 |
| 8 | Graminoid marsh | 431 | Bricks | 3682 | Island interior | 203 |
| 9 | Spartina marsh | 520 | Shadows | 947 | Acacia woodlands | 314 |
| 10 | Cattail marsh | 404 | Acacia shrublands | 248 | ||
| 11 | Salt marsh | 419 | Acacia grasslands | 305 | ||
| 12 | Mud flats | 503 | Short mopane | 181 | ||
| 13 | Water | 927 | Mixed mopane | 268 | ||
| 14 | Exposed soils | 95 | ||||
| Class No. | RF1 | RF2 | SSRF1 | SSRF2 | ASSRF |
|---|---|---|---|---|---|
| 1 | 85.30 ± 4.45 | 91.81 ± 3.05 | 93.06 ± 2.55 | 94.14 ± 0.65 | 97.11 ± 0.93 |
| 2 | 76.39 ± 5.64 | 79.18 ± 3.97 | 80.52 ± 3.87 | 82.06 ± 2.34 | 89.12 ± 3.18 |
| 3 | 87.55 ± 5.51 | 89.02 ± 4.28 | 86.27 ± 3.95 | 90.49 ± 2.99 | 92.05 ± 2.42 |
| 4 | 46.70 ± 10.14 | 57.90 ± 13.84 | 62.40 ± 9.01 | 69.40 ± 4.35 | 82.44 ± 2.30 |
| 5 | 51.41 ± 10.71 | 51.41 ± 8.28 | 53.91 ± 7.59 | 55.47 ± 5.67 | 71.81 ± 7.41 |
| 6 | 45.49 ± 11.33 | 44.29 ± 8.08 | 48.90 ± 5.11 | 47.14 ± 5.16 | 67.03 ± 4.50 |
| 7 | 90.00 ± 7.59 | 90.00 ± 4.74 | 89.05 ± 6.16 | 88.81 ± 5.27 | 90.21 ± 3.66 |
| 8 | 53.48 ± 10.84 | 65.35 ± 9.64 | 80.58 ± 9.16 | 80.87 ± 3.95 | 92.77 ± 1.57 |
| 9 | 80.58 ± 5.04 | 86.54 ± 5.69 | 89.76 ± 4.94 | 93.61 ± 2.27 | 92.90 ± 4.82 |
| 10 | 72.24 ± 7.50 | 80.68 ± 5.69 | 87.27 ± 2.77 | 89.44 ± 4.25 | 95.86 ± 3.77 |
| 11 | 91.86 ± 2.79 | 92.81 ± 2.84 | 96.35 ± 2.53 | 96.35 ± 2.14 | 97.01 ± 0.90 |
| 12 | 74.43 ± 7.17 | 79.50 ± 7.12 | 84.63 ± 4.69 | 87.36 ± 2.95 | 86.84 ± 3.36 |
| 13 | 99.16 ± 0.54 | 99.11 ± 0.58 | 99.27 ± 0.58 | 99.23 ± 0.45 | 99.29 ± 0.47 |
| OA | 78.33 ± 1.46 | 82.76 ± 0.51 | 86.19 ± 0.91 | 87.91 ± 0.52 | 91.90 ± 0.65 |
| AA | 73.45 ± 1.73 | 77.53 ± 0.75 | 80.92 ± 0.84 | 82.77 ± 0.69 | 88.46 ± 0.88 |
| kappa | 75.87 ± 1.64 | 80.78 ± 0.59 | 84.62 ± 1.01 | 86.53 ± 0.58 | 90.97 ± 0.72 |
| Class No. | RF1 | RF2 | SSRF1 | SSRF2 | ASSRF |
|---|---|---|---|---|---|
| 1 | 67.68 ± 5.50 | 79.83 ± 4.18 | 85.38 ± 1.79 | 86.79 ± 1.97 | 89.77 ± 1.20 |
| 2 | 55.52 ± 6.67 | 90.47 ± 3.24 | 95.98 ± 1.56 | 96.52 ± 0.97 | 97.17 ± 0.50 |
| 3 | 53.11 ± 9.48 | 44.60 ± 11.06 | 53.37 ± 5.12 | 51.45 ± 8.33 | 59.64 ± 6.70 |
| 4 | 86.37 ± 6.84 | 79.71 ± 8.25 | 85.33 ± 3.52 | 82.97 ± 4.37 | 87.28 ± 1.54 |
| 5 | 98.98 ± 0.26 | 98.36 ± 0.51 | 98.20 ± 0.76 | 98.16 ± 0.77 | 97.79 ± 0.54 |
| 6 | 56.95 ± 10.49 | 45.22 ± 8.96 | 45.77 ± 6.38 | 50.34 ± 4.68 | 56.04 ± 3.95 |
| 7 | 76.86 ± 14.91 | 66.65 ± 14.60 | 73.40 ± 4.94 | 77.86 ± 4.19 | 73.61 ± 2.93 |
| 8 | 67.87 ± 8.47 | 79.77 ± 7.15 | 80.21 ± 4.04 | 84.61 ± 4.78 | 84.78 ± 5.01 |
| 9 | 99.97 ± 0.08 | 99.39 ± 0.43 | 99.50 ± 0.46 | 99.66 ± 0.40 | 99.37 ± 0.55 |
| OA | 63.87 ± 2.99 | 79.26 ± 0.87 | 83.67 ± 0.55 | 84.92 ± 0.78 | 86.90 ± 0.75 |
| AA | 73.70 ± 1.73 | 76.00 ± 1.85 | 79.68 ± 1.16 | 80.93 ± 0.98 | 82.82 ± 0.98 |
| kappa | 55.35 ± 3.18 | 72.12 ± 1.13 | 77.84 ± 0.81 | 79.53 ± 1.11 | 82.27 ± 1.03 |
| Class No. | RF1 | RF2 | SSRF1 | SSRF2 | ASSRF |
|---|---|---|---|---|---|
| 1 | 97.87 ± 2.00 | 99.44 ± 0.65 | 98.98 ± 1.27 | 99.72 ± 0.45 | 100 ± 0.00 |
| 2 | 95.75 ± 2.37 | 92.50 ± 5.53 | 96.25 ± 4.29 | 97.50 ± 4.08 | 93.75 ± 4.29 |
| 3 | 89.60 ± 6.10 | 90.30 ± 4.81 | 92.90 ± 3.76 | 95.00 ± 2.36 | 100 ± 0.00 |
| 4 | 87.09 ± 2.42 | 88.26 ± 3.26 | 92.33 ± 3.25 | 93.49 ± 2.91 | 99.76 ± 0.49 |
| 5 | 77.57 ± 4.60 | 78.50 ± 3.99 | 81.12 ± 3.73 | 80.09 ± 3.47 | 90.93 ± 2.46 |
| 6 | 49.07 ± 10.51 | 53.46 ± 7.14 | 63.93 ± 5.24 | 74.30 ± 6.80 | 80.65 ± 3.61 |
| 7 | 90.38 ± 2.91 | 94.47 ± 2.71 | 97.48 ± 1.31 | 97.57 ± 1.54 | 98.93 ± 0.85 |
| 8 | 86.42 ± 9.33 | 90.12 ± 4.39 | 94.44 ± 2.62 | 95.93 ± 2.47 | 99.87 ± 0.39 |
| 9 | 64.64 ± 12.20 | 71.20 ± 7.87 | 82.16 ± 4.67 | 85.36 ± 2.36 | 95.12 ± 1.79 |
| 10 | 74.65 ± 12.13 | 81.72 ± 9.55 | 85.66 ± 6.38 | 87.47 ± 4.98 | 95.25 ± 2.38 |
| 11 | 83.28 ± 5.56 | 87.30 ± 4.66 | 91.48 ± 3.67 | 92.54 ± 2.43 | 96.89 ± 1.89 |
| 12 | 92.64 ± 5.12 | 92.64 ± 4.72 | 92.92 ± 2.81 | 95.14 ± 1.76 | 95.14 ± 2.95 |
| 13 | 69.44 ± 6.78 | 81.87 ± 6.95 | 87.95 ± 4.07 | 87.38 ± 3.67 | 93.74 ± 2.45 |
| 14 | 97.63 ± 1.94 | 97.63 ± 1.94 | 97.11 ± 3.39 | 99.21 ± 1.27 | 93.16 ± 3.96 |
| OA | 80.42 ± 0.78 | 84.16 ± 1.22 | 88.56 ± 0.70 | 90.46 ± 0.65 | 95.34 ± 0.37 |
| AA | 82.57 ± 0.72 | 85.67 ± 0.97 | 89.62 ± 0.73 | 91.48 ± 0.65 | 95.23 ± 0.40 |
| kappa | 78.83 ± 0.84 | 82.85 ± 1.32 | 87.79 ± 0.88 | 89.66 ± 0.71 | 94.84 ± 0.40 |
| Data Size | DRDbSSAL | CASSL | MCLU-ECBD | MS-cSV | EQB | ASSRF |
|---|---|---|---|---|---|---|
| 200 | 90.58 ± 0.76 | 89.24 ± 0.66 | 89.15 ± 0.97 | 88.35 ± 0.71 | 90.00 ± 0.23 | 91.90 ± 0.65 |
| 400 | 92.22 ± 0.87 | 91.76 ± 0.83 | 89.96 ± 0.79 | 89.50 ± 0.54 | 92.23 ± 0.38 | 93.81 ± 0.32 |
| 600 | 93.43 ± 0.10 | 92.77 ± 0.21 | 91.08 ± 0.46 | 89.96 ± 0.91 | 93.43 ± 0.23 | 94.68 ± 0.39 |
| 800 | 93.48 ± 0.04 | 93.03 ± 0.23 | 93.05 ± 0.20 | 91.03 ± 0.49 | 93.40 ± 0.10 | 94.76 ± 0.24 |
| 1000 | 93.47 ± 0.06 | 93.37 ± 0.31 | 93.46 ± 0.10 | 91.15 ± 0.65 | 93.41 ± 0.16 | 94.79 ± 0.21 |
| Data Size | DRDbSSAL | CASSL | MCLU-ECBD | MS-cSV | EQB | ASSRF |
|---|---|---|---|---|---|---|
| 200 | 85.97 ± 2.61 | 85.30 ± 0.63 | 84.74 ± 1.49 | 83.84 ± 1.96 | 85.07 ± 1.16 | 86.90 ± 0.75 |
| 400 | 90.37 ± 0.73 | 88.00 ± 1.01 | 88.23 ± 0.81 | 87.30 ± 1.33 | 88.89 ± 0.31 | 91.56 ± 0.54 |
| 600 | 92.04 ± 0.69 | 89.40 ± 1.01 | 89.31 ± 0.60 | 88.77 ± 0.95 | 90.32 ± 0.49 | 93.21 ± 0.39 |
| 800 | 92.54 ± 0.06 | 90.35 ± 0.73 | 89.78 ± 2.76 | 89.65 ± 0.69 | 91.48 ± 0.41 | 93.82 ± 0.14 |
| 1000 | 93.03 ± 0.07 | 90.83 ± 0.70 | 90.59 ± 2.18 | 90.59 ± 1.04 | 92.01 ± 0.34 | 94.19 ± 0.18 |
| Data Size | DRDbSSAL | CASSL | MCLU-ECBD | MS-cSV | EQB | ASSRF |
|---|---|---|---|---|---|---|
| 200 | 96.80 ± 0.41 | 95.33 ± 0.25 | 95.21 ± 0.48 | 94.59 ± 0.39 | 94.96 ± 0.35 | 95.34 ± 0.37 |
| 400 | 96.94 ± 0.12 | 96.72 ± 0.36 | 96.79 ± 0.18 | 96.81 ± 0.14 | 96.75 ± 0.19 | 96.81 ± 0.25 |
| 600 | 96.99 ± 0.00 | 97.03 ± 0.13 | 96.75 ± 0.08 | 96.91 ± 0.09 | 96.98 ± 0.13 | 97.06 ± 0.09 |
| 800 | 96.99 ± 0.01 | 97.03 ± 0.13 | 96.88 ± 0.07 | 96.91 ± 0.09 | 97.04 ± 0.11 | 97.12 ± 0.03 |
| 1000 | 97.03 ± 0.03 | 97.03 ± 0.13 | 96.88 ± 0.04 | 96.80 ± 0.04 | 97.02 ± 0.13 | 97.13 ± 0.02 |
| Time (s) | KSC | PaviaU |
|---|---|---|
| DRDbSSAL | 1785.3 | 4751.8 |
| CASSL | 1263.5 | 3354.2 |
| MCLU-ECBD | 305.8 | 1241.7 |
| MS-cSV | 3165.8 | 8745.6 |
| EQB | 267.55 | 879.6 |
| ASSRF | 967.3 | 2235.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Cao, G.; Li, X.; Wang, B.; Fu, P. Active Semi-Supervised Random Forest for Hyperspectral Image Classification. Remote Sens. 2019, 11, 2974. https://doi.org/10.3390/rs11242974
Zhang Y, Cao G, Li X, Wang B, Fu P. Active Semi-Supervised Random Forest for Hyperspectral Image Classification. Remote Sensing. 2019; 11(24):2974. https://doi.org/10.3390/rs11242974
Chicago/Turabian StyleZhang, Youqiang, Guo Cao, Xuesong Li, Bisheng Wang, and Peng Fu. 2019. "Active Semi-Supervised Random Forest for Hyperspectral Image Classification" Remote Sensing 11, no. 24: 2974. https://doi.org/10.3390/rs11242974
APA StyleZhang, Y., Cao, G., Li, X., Wang, B., & Fu, P. (2019). Active Semi-Supervised Random Forest for Hyperspectral Image Classification. Remote Sensing, 11(24), 2974. https://doi.org/10.3390/rs11242974