Use of UAV Photogrammetric Data for Estimation of Biophysical Properties in Forest Stands Under Regeneration

Abstract

The objective of this study was to assess the use of unmanned aerial vehicle (UAV) data for modelling tree density and canopy height in young boreal forests stands. The use of UAV data for such tasks can be beneficial thanks to the high resolution and reduction of the time spent in the field. This study included 29 forest stands, within which 580 clustered plots were measured in the field. An area-based approach was adopted to which random forest models were fitted using the plot data and the corresponding UAV data and then applied and validated at plot and stand level. The results were compared to those of models based on airborne laser scanning (ALS) data and those from a traditional field-assessment. The models based on UAV data showed the smallest stand-level $RMSE$ values for mean height (0.56 m) and tree density (1175 trees ha⁻¹). The $RMSE$ of the tree density using UAV data was 50% smaller than what was obtained using ALS data (2355 trees ha⁻¹). Overall, this study highlighted that the use of UAVs for the inventory of forest stands under regeneration can be beneficial both because of the high accuracy of the derived data analytics and the time saving compared to traditional field assessments.

1. Introduction

1.1. Background

Updated and accurate information on forest resources is required for good management decisions. Currently in Scandinavia, forest management inventories (FMI) are carried out at intervals of 10–20 years. Hence, for some forest stands the information may be unreliable for decision-making. A key aspect in modern precision forestry practices is to ensure updated and reliable information. This is especially true when the forest structure is changing rapidly because of rapid growth such as in the young stages of stand development. Within the context of this study we refer to forest stands under regeneration as stands that have been harvested and where the next tree generation is regenerated either through planting or through natural seed dispersal, and where the dominant trees have not yet reached merchantable size (i.e., stands in maturity class II sensu ; Antón-Fernández and Astrup [1]). Such forests stands accounts for 17% (or 15.1 mill. ha) of the total productive forest area in Norway [2]. Current operational FMI methods do not sufficiently capture reliable information on biophysical forest properties in stands under regeneration. Better information on tree density and stand mean height can lead to better planning and implementation of silvicultural treatments in stands under regeneration (e.g., pre-commercial thinning). The use of unmanned aerial vehicles (UAVs) in forest inventory has proven to produce accurate results both for small-scale forest management inventories [3,4,5,6,7] as well as for large-scale forest inventories [8,9]. In addition to the ability to capture very fine resolution information on the forest canopy, UAVs are increasingly used thanks to their versatility and availability. Nonetheless, it is not yet clear under which conditions drone applications are cost-effective, and the lack of such information is currently hindering an extensive operational use of UAVs in the forest sector.

In order to increase the cost-effectiveness of the inventory of stands under regeneration, several authors have attempted to use remotely sensed data such as space borne imagery [10,11,12], aerial imagery [13] or airborne laser scanning (ALS) data [14,15,16] to model such biophysical properties. While these data sources may be valuable for mapping stands under regeneration properties on a large scale, the associated uncertainties are often too large for operational forest management and the derived data can be rapidly outdated for the planning of silvicultural treatments. In particular, these studies highlighted the poor predictive accuracy of tree density, which is a crucial variable for decision-making in stands under regeneration. This is due both to the profound impact of tree density on the need for pre-commercial thinning as well as the associated labour costs [17]. As a result, current operational practices rely on field checks to estimate stand level values for mean height and tree density. One of the main limitations of using ALS data is that the point density of ALS data commonly acquired for forest inventory (1–5 points m⁻²) is not adequate to detect small objects such as young trees. Pitt et al. [18] highlighted the importance of using very high-resolution remotely sensed data for stands under regeneration. More specifically, Pouliot et al. [13] suggested that a crown size to pixel or point ratio of 15:1 (i.e., 15 pixel or points needed within each tree crown) is required to detect single trees in stands under regeneration. In this regard, the flexible acquisition of very high-resolution (1–5 cm) 3D and spectral data by UAVs has significant potential for inventorying stands under regeneration. Further advantages of using UAVs over field checks are that they may allow for i) reduced time spent in the field and ii) production of high-quality maps of the variables of interest.

Most research on the use of UAVs for forest inventory has focused on middle-aged and mature forests [3,4,5,6,7]. Only two studies have assessed the possibility to adopt UAV data to address the need to provide information for stands under regeneration [19,20]. Goodbody et al. [19] used UAV photogrammetric data to classify regeneration stands into three of dominant species classes (i.e., conifer, deciduous, and ground), and to assess the area extent and height of each class. Despite their results being encouraging, the authors state that the estimation and mapping of tree density remains a difficult task. A step forward in this direction was done by Feduck et al. [20], who developed a sampling method to assess the number of coniferous seedlings in raw UAV images. Their results were promising as the method was able to detect approximately 76% of the seedlings. Nevertheless, their method has the disadvantage that it relies on UAV leaf-off data, which must be acquired in a limited period between snowmelt and the beginning of the vegetative season. It is therefore evident that there is a need to assess the possibility to derive reliable information about the biophysical properties of stands under regeneration using the automated processing of UAV data.

1.2. Objective

The objective of this study was to assess the possibility to use UAV photogrammetric data to model relevant biophysical forest variables in stands under regeneration: mean height ($H_m$; m), mean height of crop trees ($H_c$; m), tree density ($N$; trees ha⁻¹), and crop tree density ($N_c$; trees ha⁻¹). We here use the term “crop trees” for those trees considered to be left after a pre-commercial thinning. Such a variable was assessed in the field according to objective criteria (see Section 2.2). One aim of the study was to compare the results obtained with UAV with results from the alternatives: (1) field-assessment according to today’s standards, and (2) ALS data as auxiliary information.

2. Materials

2.1. Study Area

The study area was located within the properties of Romedal and Stange Commons in Stange municipality in south-eastern Norway (60.63° N; 11.41° E). The area is characterized by gentle terrain with the altitude ranging from 250–600 m above sea level. Climatically the area is moderately continental with monthly mean temperatures for July and January in the lower end of the altitudinal range at around +14 and −10 °C, respectively (data from the meteorological station Løten 240 m a.sl, situated ca. 10 km north of the study area, Norwegian Meteorological Insitute [21]). For this study, local foresters selected 29 stands in the regeneration stage where pre-commercial thinning would normally be carried out (Figure 1). The stands were selected to cover a variation in site productivity, species composition, and stand size. The area of the stands varied from 0.4 to 13 ha with an average of four ha and were equally distributed according to three stand size classes: 1–2 ha, 2–5 ha, and greater than five ha. With regard to the site index and species composition, 20 stands were dominated by Norway spruce (Picea abies (L.) Karst), with one half of these located in medium (2–4 m³ ha⁻¹ year⁻¹) and one half in high (≥4 m³ ha⁻¹ year⁻¹) productivity sites. The remaining 10 stands were dominated by Scots pine (Pinus sylvestris L.) in medium productivity sites.

2.2. Field Data

Field data were acquired in two separate field campaigns conducted by two experienced, local foresters between June and September 2018. In the first campaign, the data were gathered in 50 m² circular field plots to be used for ground truthing (“field-plot dataset”), while in the second campaign data were collected according to operational practices and included a rapid visual assessment of the stands (“field-assessed dataset”).

The field-plot dataset was collected based on a systematic, clustered sampling design. We placed four clusters in each stand according to a systematic principle with varying spacing between the clusters depending on the size of the stand. Each cluster was composed of five 50 m² circular plots, i.e., one located in the centre of the cluster and the remaining four at a 10 m distance in each cardinal direction. In total, the field-plot data comprised 116 clusters and 580 plots. Each field plot was subdivided into four quadrants of 12.5 m² each according to the cardinal directions. The field plot measurements were performed for trees having heights of at least 50 cm and included: (1) the number of trees per ha for spruce, pine, and broadleaved species, (2) the crop tree density per ha for the same tree species classification, and (3) a sample of tree heights for both of the previous categories. A maximum of 10 crop trees were selected per plot, corresponding to a stand density of up to 2000 trees ha⁻¹. These trees were further required to be uniformly distributed among the four quadrants (i.e., maximum three trees per quadrant) and to have a minimum distance between each other of 1 m. For both categories of trees (i.e., all trees and crop-trees), we systematically sampled the height of the first tree found in each quadrant in a clockwise direction. Thus, given that there were four quadrants and two sets of categories of trees, there were a maximum of eight trees included in the height sample. Tree heights were measured using a height pole for small trees and using a Vertex hypsometer [22] for larger trees. The centre point in each plot was positioned with sub-decimetre accuracy using a Topcon GR5 global navigation satellite system (GNSS) receiver [23] fitted with cellular communication for real time kinematic (RTK) correction live via the Global System for Mobile communication (GSM) network. This was done for those plots where a link to a correction signal was available (400 plots) and with sub-meter accuracy using a Topcon GR-3 differential GPS [24] with 15-min logging time for the remaining centres for which no RTK position was available. The positions of the additional four plots in each cluster were derived from the distance (10 m) and the cardinal direction to the cluster centre. The mean stand height ($H_m$) and the mean height of the crop trees ($H_c$) were calculated from the field plot data as the mean of all the trees and the mean of the crop trees, respectively. The values for $N$ and $N_c$ were scaled to per ha values. Furthermore, the field plots were aggregated to cluster level and subsequently to stand level to obtain stand level estimates of the variables of interest.

The field-assessed dataset consisted of a conventional assessment of the need for tending as is carried out operationally in todays’ forestry in Norway. This consisted of a field check where a local forester visually assessed mean height, tree density, and the tree density for crop trees. Further measurements in the field-assessed dataset included: (1) the time spent on walking from roadside to the stand of interest and back (total = 5.1 hours), and (2) the time required to perform the stand assessment (total = 10 hours).

A summary of the biophysical forest variables measured in the field-plot dataset at plot and at stand level is provided in

Table 1. Summary statistics for the field-plot dataset.

Characteristics	Minimum	Maximum	Mean
Plot level (n = 580)
$H_m$ (m)	0.5	13	2.5
$H_c$ (m)	0.5	13	3
$N$ (trees ha−1)	0	21,600	5572
$N_c$ (trees ha−1)	0	2000	1445
Stand level (n = 29)
$H_m$ (m)	0.9	6.9	2.5
$H_c$ (m)	0.9	7.7	2.9
$N$ (trees ha−1)	1440	11,360	5479
$N_c$ (trees ha−1)	570	1970	1433

.

2.3. Remotely Sensed Data

2.3.1. ALS data

Airborne laser scanning (ALS) data were freely accessible from a nationwide ALS scan in Norway [25]. The ALS data were acquired during three days in the beginning of June 2016 using an Optech ALTM Titan MV [26] with a pulse density of 5 points m⁻² and a maximum scanning angle of 20 degrees. Further details on the used ALS data are available in the project report produced by the data provider [27]. The ground points were classified using an initial progressive densification filtering algorithm [28] followed by a manual quality check. A digital terrain model (DTM) was obtained from the ground classified points and subtracted to each point height value to obtain a normalized point cloud with height values in m above ground.

2.3.2. UAV Data

We acquired UAV data during August 2018 using a DJI Phantom 4 PRO [29]. A single UAV acquisition was performed for each of the stands and included the placement and RTK measurement of five ground control points (GCPs) and the actual UAV flight. The choice of using five GCPs per stand was determined by previous experiences in UAV data acquisition [8]. In some cases where stands were close to each other, a single UAV flight was required to cover both stands. The image acquisitions were performed throughout the day irrespective of the varying light and atmospheric conditions. The only factors preventing a UAV data acquisition were rain and winds >10 m sec⁻¹. Image acquisition parameters are summarized in

Table 2. Summary of the image acquisition parameters.

Parameter	Value
Flight altitude	110 m
Ground sampling distance	3 cm
Forward overlap	90%
Side overlap	80%
Flight speed	5 m sec−1

.

The entire UAV campaign lasted two weeks and included the acquisition of UAV data and additional measurements which were out of the scope of this study. In regard to the UAV data acquisition, we spent a total of 5.3 flight hours for all of the stands. This included the setup of the UAV, the actual flight, and packing up the UAV. Furthermore, the total time required to walk to the home point (i.e., the point where the UAV takes off and lands) from the roadside was 2.5 hours. There were no difficulties encountered during the UAV mission, which were only limited by the day length.

The imaging sensor used was a 1-inch 20 megapixels red, green, and blue (RGB) sensor with mechanical shutter and focal length of 8.8 mm which was integrated in the Phantom 4 Pro [29]. In order to reduce image blurriness, the shutter speed was fixed to 1/1000 and the aperture and ISO were varied according to the light conditions.

We processed the UAV images using Agisoft Photoscan version 1.4.1 [30], and generated three products for each stand: (1) an orthomosaic with pixel size of 3 cm × 3 cm, (2) a point cloud with a point density of approximately 300 points m⁻² classified into ground and non-ground points, and (3) a digital surface model (DSM) with pixel size of 6 cm × 6 cm. The most relevant parameters used for photogrammetric reconstruction in Photoscan are summarized in

Table 3. Summary of the most relevant parameters adopted in the photogrammetric processing. The parameters were for Agisoft Photoscan. Further parameters are available in the software but here we report only the most relevant ones and those that were modified from default settings for this particular application.

Processing Step	Parameter Name	Parameter Value
Alignment	Accuracy	Highest
Optimization	Default
Ground control points placement	Manual
Densification	Quality	High
	Depth filtering	Mild
Ground classification	Max angle (°)	10
	Max distance (m)	1
	Cell size (m)	50

. The classification of the ground points was done using the same algorithm as for the ALS data [28] using the following parameters determined by a trial and error approach: maximum angle of 10°, maximum distance of 1 m, and cell size of 50 m. The derived DTM was used in a similar fashion to ALS data to normalize the point cloud by subtracting for each point height value the respective height of the terrain.

3. Methods

3.1. Variable Extraction

We extracted 92 candidate explanatory variables from the UAV data and included the following categories of variables: (1) spectral, (2) DSM, and (3) normalized point cloud. These categories of variables were selected to capture different components characterizing UAV photogrammetric data, namely: the spectral and the structural components. The spectral variables were calculated using the digital numbers corresponding to the red, green, and blue bands for the pixels corresponding to each plot. From the raw digital number values, the band mean values ($R_m$, $G_m$, and $B_m$) and standard deviations ($R_{sd}$, $G_{sd}$, and $B_{sd}$) were computed. Further spectral variables included the mean ($G/R_m$, $B/R_m$, and $G/B_m$) and standard deviation ($G/R_{sd}$, $B/R_{sd}$, and $G/B_{sd}$) of band ratios, calculated as the ratio of the difference between the nominator and denominator and the sum of nominator and denominator (e.g.,$G/R=green-red/green+red$). Such ratios were computed in order to provide more stable measures of the radiance across different UAV acquisitions compared to single band values [31]. Among the different band ratios, preliminary analysis revealed $G/R$ to be the most correlated to the studied variables. As a result, this raster product was used to calculate textural variables using the R package “glcm” [32]. The textural variables included the mean ($sMEA{N}_m$,$sVARIANC{E}_m$, $sHOMOGENEIT{Y}_m$, $sCONTRAS{T}_m$, $sDISSIMILARIT{Y}_m$, $sENTROP{Y}_m$, and $sSECOND\_MOMEN{T}_m$) and standard deviation ($sMEA{N}_{sd}$,$sVARIANC{E}_{sd}$, $sHOMOGENEIT{Y}_{sd}$, $sCONTRAS{T}_{sd}$, $sDISSIMILARIT{Y}_{sd}$, $sENTROP{Y}_{sd}$, and $sSECOND\_MOMEN{T}_{sd}$) of the mean, variance, homogeneity, contrast, dissimilarity, entropy, and second moment. All the variables were calculated using a window size of 3 × 3 pixels and a 45 degree shift. The latter parameter determined the direction (45°) along which the textural variables were calculated. This was selected instead of using all the directions in order to limit computational time.

The use of DSM variables was motivated by the findings of Giannetti et al. [33] who showed that DTM-independent variables obtained directly from UAV DSMs can also be useful in describing forest structures. Furthermore these variables remove the need for the normalization of the point cloud, which is a step that can introduce undesired random errors in the CHMs and further propagate in the developed models. Such errors can be especially severe when using poor DTMs such as those obtained in stands under regeneration using UAV photogrammetric data or even ALS data (i.e., reduced penetration of pulses to the ground and larger uncertainty of the ground classification of ALS data). The DSM variables were computed using the raw DSM values (i.e., in m above sea level) of all pixels within the area corresponding to that of each field plot and included: (1) summary statistics ($DS{M}_{min}$, $DS{M}_{max}$, $DS{M}_{mean}$, $DS{M}_{median}$, and $DS{M}_{range}$); (2) mean ($SLOP{E}_m$, $TP{I}_m$, $TR{I}_m$, $ROUGHNES{S}_m$, $FLOWDI{R}_m$) and standard deviation ($SLOP{E}_{sd}$, $TP{I}_{sd}$, $TR{I}_{sd}$, $ROUGHNES{S}_{sd}$, and $FLOWDI{R}_{sd}$) of the following topographic variables calculated using the terrain function in the R package “raster” [34]: slope, topographical position index, terrain roughness index, roughness, and flow direction. These variables were used to describe the horizontal variations of tree canopy height and possibly different crown patterns describing different tree species (e.g., conifer crowns characterized by larger slopes and variations in height compared to thickets of broadleaved species). To provide further description of the horizontal variations of the canopy height, textural variables were calculated using the DSM with the same parameters as previously described for spectral-textural variables. The mean ($dsmMEA{N}_m$, $dsmVARIANC{E}_m$, $dsmHOMOGENEIT{Y}_m$, $dsmCONTRAS{T}_m$, $dsmDISSIMILARIT{Y}_m$, $dsmENTROP{Y}_m$, $dsmSECOND\_MOMEN{T}_m$) and standard deviation ($dsmMEA{N}_{sd}$, $dsmVARIANC{E}_{sd}$, $dsmHOMOGENEIT{Y}_{sd}$, $dsmCONTRAS{T}_{sd}$, $dsmDISSIMILARIT{Y}_{sd}$, $dsmENTROP{Y}_{sd}$, $dsmSECOND\_MOMEN{T}_{sd}$) were then computed using all pixels within the plot.

The normalized point cloud variables were used to describe the 3D structure of the canopy. The point cloud normalization was performed by subtracting the digital terrain model (DTM) from each point’s height value. The result was a unit conversion from height above sea level to height above ground. The DTMs used for normalization of the UAV data were generated using the ground classified points from the UAV photogrammetric point cloud (see Section 2.3.2). Among these variables were the commonly used height percentiles ($P_{10}$, $P_{20}$, …,$P_{95}$, $P_{100}$) and point density variables ($d_{10}$, $d_{20}$, …, $d_{100}$). The latter were calculated for equally spaced vertical layers, defined as tenths of the distance between the 95th percentile and the lowest canopy height. The densities were computed as the proportion of points above the 1st, …, 9th (d0, …, d9) fraction to the total number of points. Further variables derived from the normalized point cloud were: the percentage of ground points ($groun{d}_{\%}$), and the number of local maxima calculated for window sizes equal to all the odd numbers between 3 and 29 pixels ($locMa{x}_3$, $locMa{x}_5$, …, $locMa{x}_{27}$, and $locMa{x}_{29}$). This last group of variables was used as previous research by Giannetti et al. [33] demonstrated the usefulness of such variables in modelling forest biophysical variables.

We extracted corresponding variables from the ALS data, with the difference that spectral variables were excluded and that the DTM used for the normalization was generated using the ALS ground classified points by the data vendor. For both datasets, we derived the variables both for each field plot and for a grid of cells with area equal to that of the field plot size, tessellating all the stands included in the analysis.

3.2. Modelling Biophysical Forest Properties

The forest biophysical variables tree density and canopy height were modelled using a random forest (RF) model implemented in the R package “randomForest” [35]. The random forest is an ensemble learning method which relies on the generation of regression trees and on the aggregation of their results. The regression trees are generated through bagging [36] according to which successive trees are randomly selected through bootstrapping of the response and explanatory variables. Each node is then split according to the best split among a subset of explanatory variables. The choice of using a random forest model rather than alternative machine learning models or even linear regression was motivated by the fact that it has been widely proven to perform well and to be robust against overfitting [37]. The number of regression trees was set to 500, as the error rates were reaching the asymptote for this value. Two variables were tried at each split as this was found to be the most suitable value based on a trial and error approach. A further advantage of the random forest model is that it is not very sensitive to modifying the two parameters [35]. For each model, the proportion of the variance explained ($R^2$) was:

$$R^2=1-\frac{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-\overline{y}\right)}^2}$$

(1)

where $y_i$ and ${\widehat{y}}_i$ are equal to the field plot data and the predicted values, respectively for the ith plot ($i$ = 1, …, $n$) for each variable of interest, and $\overline{y}$ is the average of all the field measured values in the sample.

We validated the models by means of a leave-one-out approach, either leaving out a plot or leaving out a stand. These consisted in: (1) the iterative removal of either a single plot or the four clusters within a stand, (2) fitting a random forest model on the remaining set of field plots, and (3) the prediction of the variables of interest on the observations that were left out. The cross-validated predictions were then used to calculate the root mean square error ($RMSE$), the mean difference ($MD$), and the respective values as percentage of the mean ($RMS{E}_{\%}$ and $M{D}_{\%}$). The $RMSE$ and $MD$ were calculated according to:

$$RMSE= \sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}{n}}$$

(2)

$$MD=\frac{{{\displaystyle \sum }}_{i=1}^n\left(y_i-{\widehat{y}}_i\right)}{n}$$

(3)

Finally, the presence of significant systematic errors in the residuals was tested using a two-tailed t-test at the 95% significance level.

4. Results

For the selected UAV based models, the spectral variables were never among the five most important explanatory variables (

Table 4. Summary of the five most important variables selected by the random forest algorithm for each modelled variable and different remotely sensed data source (i.e., unmanned aerial vehicle, UAV; and airborne laser scanning, ALS).

Modelled Variable	UAV	ALS
$H_m$ (m	$SLOP{E}_m$, $locMa{x}_3$, $locMa{x}_5$, $d_{10}$, $groun{d}_{\%}$	$P_{60}$,$DS{M}_{median}$,$P_{70}$, $P_{40}$, $P_{50}$
$H_c$ (m)	$SLOP{E}_m$,$groun{d}_{\%}$,$locMa{x}_3$, $locMa{x}_5$, $d_{10}$	$P_{60}$,$DS{M}_{median}$,$P_{70}$, $ROUGHNES{S}_{sd}$, $TR{I}_{sd}$
$N$ (trees ha−1)	$DS{M}_{mean}$ , $DS{M}_{median}$, $dsmSECOND\_MOMEN{T}_m$, $DS{M}_{min}$, $DS{M}_{max}$	$P_{90}$, $DS{M}_{max}$,$ROUGHNES{S}_{sd}$, $P_{60}$, $groun{d}_{\%}$
$N_c$ (trees ha−1)	$P_{10}$, $DS{M}_{median}$, $dsmSECOND\_MOMEN{T}_m$, $DS{M}_{mean}$,$DS{M}_{min}$	$P_{90}$, $groun{d}_{\%}$, $P_{80}$,$P_{80}$, $SLOP{E}_{sd}$

). Different categories of explanatory variables had different behaviours in regard to their explanatory power for the different independent variables of interest. The DSM variables were more important for $N$ and $N_c$ while the normalized point cloud-variables proved to be more important in modelling $H_m$ and $H_c$. For $H_m$ and $H_c$the percentage of ground points over the total ($groun{d}_{\%}$) and local maxima counts for window sizes of 3 ($locMa{x}_3$) and 5 ($locMa{x}_5$) were always among the five most important variables. For $N$ and $N_c$, the DSM raw height values (in m above sea level) were the most important variables together with a textural variable from the DSM ($dsmSECOND\_MOMEN{T}_m$,). In regard to ALS data, thanks to the availability of a good quality DTM, the models always included height percentiles. Interestingly, for ALS data, the models included variables from the DSM raw height values ($DS{M}_{median}$) and derived topographical variables ($ROUGHNES{S}_{sd}$).

The random forest models fitted using the field and UAV data were able to explain at least 45% of the variance in the forest biophysical properties using the field-plot dataset for ground-truthing, with a maximum of 61% for $N$ (

Table 5. Summary of the accuracy in terms of root mean square error, ($RMSE$) its value as percentage of the mean ($RMS{E}_{\%}$), the mean difference ($MD$) and its value as percentage of the mean ($M{D}_{\%}$) for the studied forest biophysical variables and auxiliary dataset.

Characteristics	Auxiliarydata	Measurement Unit	R2	RMSE	RMSE%	MD	MD%	Significance a
$H_m$ (m)	Field-assessed	Stand	-	1.33	55.2	−0.64	−27.3	*
	ALS	Plot	0.53	0.80	32.0	−0.04	−1.8	NS
		Stand		0.76	31.6	0.30	12.5	NS
	UAV	Plot	0.52	0.77	30.9	−0.02	−0.8	NS
		Stand	-	0.56	23.6	0.09	3.7	NS
$H_c$ (m)	ALS	Plot	0.53	0.97	32.6	0.009	0.3	NS
		Stand		0.9	32.1	0.34	12.3	NS
	UAV	Plot	0.56	0.91	30.3	0.01	0.2	NS
		Stand	-	0.64	23.2	0.07	2.7	NS
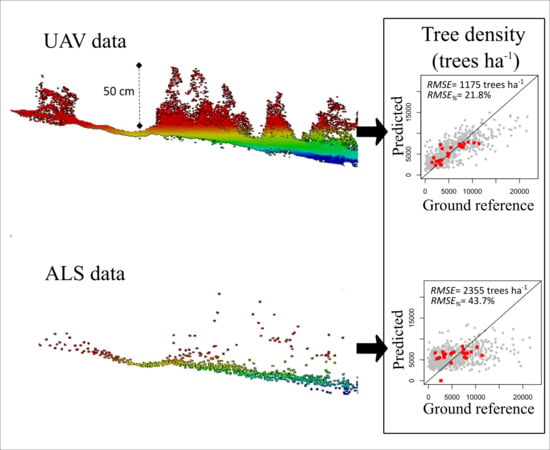
$N$ (trees ha−1)	Field-assessed	Stand	-	2640	49.0	1398	25.9	*
	ALS	Plot	0.18	2979	53.4	−103	−1.8	NS
		Stand		2355	43.7	−481.5	−8.9	NS
	UAV	Plot	0.61	2024	36.3	−86	−1.5	NS
		Stand	-	1175	21.8	−62	−1.1	NS
$N_c$ (trees ha−1)	Field-assessed	Stand	-	284	19.7	−155	−8.1	NS
	ALS	Plot	0.12	413	28.4	15	1.00	NS
		Stand		352	24.6	250.35	17.5	*
	UAV	Plot	0.45	305	21.1	6	0.4	NS
		Stand	-	185	13	35	2.4	NS

^a level of significance: NS = not significant, * <0.05.

). The predictive accuracies of the UAV data-based models in terms of $RMS{E}_{\%}$ were in the range of 21.1%–36.3% and 13%–23.6% at plot and stand level, respectively. For the ALS data, model performance was similar to the UAV data-based ones regarding the height-related variables ($H_m$ and $H_c$), while the performances dropped when modelling $N$ and $N_c$. The ALS based models were able to explain only 18% and 12% of the variance of $N$ and $N_c$, respectively, corresponding to plot-level $RMS{E}_{\%}$ values of 53% and 28%. As expected, for all variables there was a decrease in $RMS{E}_{\%}$ when increasing the scale from plot to stand level. The decrease was largest for $N$ (14% reduction) and smallest for $H_m$ and $H_c$ (7% reduction). Other than for the stand-level estimation of $N_c$ using ALS data, the assessment of the models’ residuals revealed the absence of significant systematic errors. On the contrary, the estimates obtained through field assessment revealed the presence of systematic errors for all the variables that were assessed in the field.

The scatterplots of the predicted versus the ground reference values revealed an overall trend of under-prediction for plots (see grey dots in Figure 2) having many tall trees, i.e., mean height larger than 5–6 m and more than 10,000 trees ha⁻¹. Because of the narrower ranges of stand level values (i.e., red squares in Figure 2) this saturation effect was considerably reduced.

Further analysis included the assessment of the $RMSE$ for incremental tree density classes. This revealed that for the interval between 2000 and 3000 trees ha⁻¹, the $RMSE$ (approx. 1000 trees ha⁻¹) was significantly smaller (p-value < 0.05) than the other stem density classes. The maximum $RMSE$ was found in plots with more than 10,000 trees ha⁻¹ (see Figure 3). Interestingly, there was a peak in the $RMSE$ value for the class between 4000 and 5000 trees ha⁻¹ which was, however, significantly different only when compared to the subsequent class (5000–6000 trees ha⁻¹). The plots within the 4000–5000 trees ha⁻¹ class were mostly dominated by deciduous species, which differed from the neighbouring classes which were mostly dominated by coniferous species. Beyond this difference, there was no apparent reason for such an increase. We attributed this to a combination of randomness in the field measured data and the associated residuals together with the use of the current classification into classes of 1000 trees ha⁻¹.

5. Discussion

To the authors’ knowledge, this study is the first example in the literature where a combination of field and UAV data were used to model key forest properties in a forest at the regeneration phase. The results indicated an increased accuracy when going from field-assessment via ALS to UAV data-based. It is important to highlight that a sample of four clusters per stand may not be sufficient to estimate “true” values for the studied biophysical forest properties. However, given the data available in this study, the field-measured dataset was the most suitable ground-reference dataset to be used for validating the field-assessed and UAV estimates. With regard to the field-assessment, not only the errors in terms of $RMS{E}_{\%}$ were the largest (55% and 49% for $H_m$ and $N$, respectively) but also the estimates affected by significant systematic errors of −27% for $H_m$ and 26% for$N$ (0.001 < p-values < 0.05). Models based on ALS data had a temporal mismatch between ALS and field data acquisitions of approximately two years. This difference may have contributed to a poorer performance of ALS over UAV data. However, the accuracy found for ALS predictions was in line with the results by Ørka et al. [16], and thus provided a meaningful comparison in this study. For all the studied biophysical variables, UAV data resulted in a stand-level decrease in $RMS{E}_{\%}$; however, this was marked for $N$ and $N_c$ with decreases in the order of 22% and 11%, respectively. With regard to $N$, we found smaller $RMSE$ and $RMS{E}_{\%}$ values than reported elsewhere in the literature regarding stands under regeneration, thus highlighting the potential of UAVs to estimate this variable. Despite the small $RMSE$, the results showed some signs of saturation resulting from the under-prediction of plots with more than 10,000–15,000 trees ha⁻¹. Even though this is a limitation of the UAV method, it may not have a substantial impact on the actual decision to perform pre-commercial thinning. The uncertainty of making such decision is minimal for very dense stands (i.e., the decision is obvious), while the potential consequences of inaccurate predictions are clear for stands with stem densities around 2000 trees ha⁻¹, which represents the threshold in many Nordic countries for the number of desired future crop trees. In this regard, the results of this study were encouraging as the errors for stands in the range of 1000–4000 trees ha⁻¹ were the smallest among the entire range of field measured tree densities. While on the one hand, the saturation may not severely affect the decision on whether or not to perform the pre-commercial thinning, it will likely have a larger effect on the estimation of the costs for such silvicultural treatments, which is often a required estimate in operational conditions. Thus, further studies should address how the UAV-based estimation of these variables can contribute to making informed and timely decisions.

As expected, we observed a reduction in the $RMSE$ values both for ALS and for UAV data when going from plot to stand level. Such a reduction is typical of remotely sensed data based models and can be explained by i) the reduction in the occurrence of extreme observations because of the averaging of plot level values to the stand level, and ii) the reduction of plot-edge effects. The latter represent a source of noise which is generated by the mismatch between the positions of the stem of the field measured trees and the tree crowns [38]. Thus edge effects are either trees which have not been measured but that have the crown within the plot or stand area, or trees that have been measured but the majority of the crown lies outside of the plot or stand area [39]. Edge effects decrease when decreasing the perimeter-to-area ratio of the area units used in the validation [39]. In this study the area of the field plots was very small (50 m²), which can explain the substantial reduction in RMSE when going from plot to stand level. In regard to the differences between models for variables including all trees ($H_m$ and $N$) rather than just the crop trees ($H_c$ and $N_c$), this study showed that the difference in $RMSE$ was larger for stem density related variables compared to the height variables. This may be explained by the fact that when looking only at crop trees, the mean number of trees was significantly reduced (i.e., reduced by 74%) compared to the total number, while the mean heights of the crop trees differed less from that of the mean tree height of the entire stand (i.e., increased by 20%).

When comparing the current results with those of previous studies, it is important to note the large differences in the sampling designs, variables measured, and ranges of these variables across the different studies. As an example, in the study by Næsset and Bjerknes [14], who explored the potential to derive stand-level attributes in young forest from ALS data, the range for field measured tree density was limited to 1650–7100 trees ha⁻¹. In a corresponding study by Ørka et al. [16], it was as wide as 312–71250 trees ha⁻¹. Such large differences in range may have reflected on the predictive accuracy of $N$, resulting in $RMS{E}_{\%}$ of 28.8% in the study by Næsset and Bjerknes [14] and of 46.6%–82.7% in the study by Ørka et al. [16]. The range of plot-level field measured N for our study was 0–21,600 trees ha⁻¹ and the results obtained using the ALS data were more in line with the findings by Ørka et al. [16] than those by Næsset and Bjerknes [14]. Overall, the $RMS{E}_{\%}$ found in this study was consistent with the results by Ørka et al. [16] suggesting UAV data can be a more suitable data source than ALS data for assessing biophysical properties of stands under regeneration. A gain in performance relative to ALS data can be attributed to the substantial increase in resolution and thus a higher possibility to detect small trees. Within the realm of passive sensing other studies used space borne [12] or manned aerial imagery [13,40] for assessing stands under regeneration biophysical properties. Wunderle et al. [12] showed how SPOT-5 pan-sharpened imagery could be used to describe the structural complexity of stands under regeneration. However, their results were not directly comparable to the ones in this study given that Wunderle et al. [12] did not report results for actual biophysical variables. Pouliot et al. [13] were able to detect 90% of conifer trees in the regeneration phase using very high resolution (5–15 cm pixels) aerial imagery. Despite these results being rather encouraging, Pouliot et al. [13] obtained these results using only field plots where the competition of broadleaves was absent. Such constraints greatly limit the application of their method especially when the information on the broadleaved-conifer competition is required to determine the need of pre-commercial thinning. While the use of large scale remotely sensing data sources can be appealing for a rough assessment over extensive areas, their use has not yet been used operationally. In this regard the advantage of using UAV data is that it can provide data analytics that can be directly used in operational planning substituting the need for costly and subjective field checks. The modelling of $H$ and $H_c$ revealed less difference between the ALS and UAV data. This result was somewhat expected given that ALS data allows the retrieval of accurate information regarding the terrain altitude and thus on the relative height of the vegetation while this is not directly applicable to UAV photogrammetric data. However, it is important to highlight that in this study no ALS digital terrain model was used, thus supporting the concept originally developed by Giannetti et al. [33], i.e., that ALS data is not necessarily required for modelling of key forestry variables.

In regard to the modelling of $N$, the only possible comparison with UAV studies addressing biophysical variables of stands under regeneration is based on the study by Feduck et al. [20], who reported an error of approximately 720 trees ha⁻¹ in a stand with an average tree density of 2980 trees ha⁻¹. Despite the limited validation (i.e., a single stand) in the study by Feduck et al. [20] and differences in the population of interest (i.e., seedlings) from this study (i.e., stands under regeneration), their figure in terms of percentage value of the mean (24.2%) were consistent with the stand-level $RMS{E}_{\%}$ reported in this study (21.8%). With regard to the comparison of $N$ modelling using UAV data in more mature forests, Puliti et al. [6] reported similar results in terms of $RMS{E}_{\%}$ (38.6%) to the current study (36.3%), which is somewhat unexpected given the larger difficulty of modelling such variables in stands under regeneration. It is true however that in their study Puliti et al. [6] acquired UAV imagery under sub-optimal atmospheric conditions and better results would be expected for mature forests from summer acquisitions.

The comparison of the man-hours needed for acquiring the stand-level information either by traditional approaches (field assessment) or UAV-based methods revealed that the total number of hours required for data acquisition was reduced by half when performing a UAV survey (total = 7.1 hours) as compared to the traditional field assessment method (total = 13.6 hours). This is due to the combination of a reduction in the need to walk to access the stand of interest and the larger efficiency of flying over a stands under regeneration stand rather than walking in it. For extrapolation to an operational context, a corresponding reduction in man-hours depend on the assumption that existing models are transferrable across study areas, i.e., that no ground surveys and no model re-fitting are required. This assumption is supported by the result from the study by Karjalainen et al. [41] who found that ALS-based models can be transferred to new areas without an excessive reduction in accuracy. Although UAV data have different characteristics due to variations in light, atmospheric and seasonal conditions, it is possible that the findings by Karjalainen et al. [41] can apply to UAV data as well. However, further studies should assess the transferability of UAV data-based models across different areas and different UAV datasets.

6. Conclusions

The objective of this study was to assess whether UAV data can be used to model relevant biophysical forest variables in stands under regeneration. The UAV data, in combination with field plot data, were used according to an area based approach, where we fitted models for each variable of interest and used these to predict the variable of interest at plot and stand level. The viability of the method was determined by comparison with methods based on alternative data sources, namely a combination of ALS and field data or a rapid field assessment done according to currently operational methods. This study demonstrated that the use of UAV data provided more accurate predictions than an ALS data or field assessments, with a reduction in the relative RMSE of 50% for stem density compared to ALS data. One of the main merits of this study was to demonstrate how the use of UAV data enabled the modelling and prediction of stem density, a variable typically associated with large errors, with unprecedented accuracy. Given the importance of accurately estimating stand level tree density for deciding whether to perform pre-commercial thinning in young forest, the results of this study indicate that UAVs may have a significant potential in providing the data needed to make more informed and timely decisions in young forests. Furthermore, our study showed that the use of UAVs may provide a more objective and accurate methodology than field assessments and that the time required for data acquisition with the former was only half of the latter. Despite the encouraging results of this study, it remains crucial in further studies to assess the contribution that UAV data have in better decision making for silvicultural treatments of stands under regeneration (e.g., pre-commercial thinning).