On-Orbit Geometric Calibration and Validation of Luojia 1-01 Night-Light Satellite
Abstract
:1. Introduction
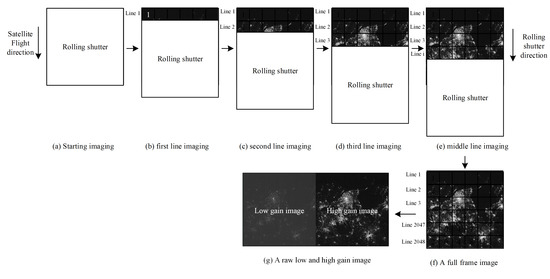
2. Methods
- (1)
- In the case in which star sensors A and B work simultaneously, the sensors measure the quaternion of their own measuring coordinate system relative to the J2000 coordinate system, which should satisfy the relationship shown in Formula (5). Assuming star sensor A as the benchmark, the installation matrix for star sensor B can be updated according to Equation (5);
- (2)
- For any star-sensitive working mode (only star sensor A working, only star sensor B working, and both star sensors working), the updated star sensor installation matrix in case (1) is adopted to determine the attitude quaternion of the satellite body coordinate system relative to the J2000 coordinate system.
- (3)
- The offset matrix is solved on the basis of case (2).
3. Results and Discussion
3.1. Study Areas and Data Sources
3.2. Results of Geometric Calibration
3.3. Verification of Absolute Positioning Accuracy
3.4. Verification of Relative Positioning Accuracy
3.4.1. Verification of Exterior Orientation Accuracy
3.4.2. Multi-Time Phase Registration Accuracy Verification
- (1)
- Match the same point from images A and B; calculate the ground coordinate corresponding to by using the RPC model of image A and SRTM; and calculate the image coordinate corresponding to by using the RPC model of image B.
- (2)
- Solve the affine model between and .
- (3)
- Using 1–3 to establish the point-to-point mapping relationship between the images A and B, resample image B based on image A. Realizing the registration of images A and B, and evaluate the registration accuracy.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, X.; Zhao, L.; Li, D.; Xu, H. Mapping Urban Extent Using Luojia 1-01 Nighttime Light Imagery. Sensors 2018, 18, 3665. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; He, G.; Long, T.; Guo, H.; Yin, R.; Leng, W.; Liu, H.; Wang, G. Potentiality of Using Luojia 1-01 Nighttime Light Imagery to Investigate Artificial Light Pollution. Sensors 2018, 18, 2900. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chen, R.; Li, D.; Zhang, G.; Shen, X.; Yu, B.; Wu, C.; Xie, S.; Zhang, P.; Li, M.; et al. Initial Assessment of the LEO Based Navigation Signal Augmentation System from Luojia-1A Satellite. Sensors 2018, 18, 3919. [Google Scholar] [CrossRef]
- LI, D.; LI, X. An Overview on Data Mining of Nighttime Light Remote Sensing. Acta Geod. Cartogr. Sin. 2015, 44, 591–601. [Google Scholar]
- El Gamal, A.; Eltoukhy, H. CMOS image sensors. IEEE Circuits Devices Mag. 2005, 21, 6–20. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, G.; Sun, Y. An Affine Motion Model for Removing Rolling Shutter Distortions. IEEE Signal Process. Lett. 2016, 23, 1250–1254. [Google Scholar] [CrossRef]
- Thanh-Tin, N.; Lhuillier, M. Self-calibration of omnidirectional multi-cameras including synchronization and rolling shutter. Comput. Vis. Image Underst. 2017, 162, 166–184. [Google Scholar] [CrossRef]
- Meingast, M.; Geyer, C.; Sastry, S. Geometric Models of Rolling-Shutter Cameras. Comput. Sci. 2005, arXiv:cs/0503076. [Google Scholar]
- Ye, W.; Qiao, G.; Kong, F.; Guo, S.; Ma, X.; Tong, X.; Li, R. PHOTOGRAMMETRIC ACCURACY AND MODELING OF ROLLING SHUTTER CAMERAS. ISPRS J. Photogramm. Remote Sens. 2016, III-3, 139–146. [Google Scholar]
- Jiang, Y.-h.; Zhang, G.; Tang, X.-m.; Li, D.; Huang, W.-C.; Pan, H.-B. Geometric Calibration and Accuracy Assessment of ZiYuan-3 Multispectral Images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4161–4172. [Google Scholar] [CrossRef]
- Tang, X.; Zhou, P.; Zhang, G.; Wang, X.; Jiang, Y.; Guo, L.; Liu, S. Verification of ZY-3 Satellite Imagery Geometric Accuracy Without Ground Control Points. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2100–2104. [Google Scholar] [CrossRef]
- Mi, W.; Cheng, Y.; Chang, X.; Jin, S.; Ying, Z. On-orbit geometric calibration and geometric quality assessment for the high-resolution geostationary optical satellite GaoFen4. ISPRS J. Photogramm. Remote Sens. 2017, 125, 63–77. [Google Scholar]
- Zhang, G.; Xu, K.; Huang, W. Auto-calibration of GF-1 WFV images using flat terrain. ISPRS J. Photogramm. Remote Sens. 2017, 134, 59–69. [Google Scholar] [CrossRef]
- Jiang, Y.-H.; Zhang, G.; Chen, P.; Li, D.-R.; Tang, X.-M.; Huang, W.-C. Systematic Error Compensation Based on a Rational Function Model for Ziyuan1-02C. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3985–3995. [Google Scholar] [CrossRef]
- Radhadevi, P.V.; Müller, R.; D’Angelo, P.; Reinartz, P. In-flight Geometric Calibration and Orientation of ALOS/PRISM Imagery with a Generic Sensor Model. Photogramm. Eng. Remote Sens. 2011, 77, 531–538. [Google Scholar] [CrossRef]
- Bouillon, A.; Breton, E.; Lussy, F.D.; Gachet, R. SPOT5 HRG and HRS first in-flight geometric quality results. In Proceedings of the International Symposium on Remote Sensing, Crete, Greece, 23–27 September 2002; pp. 212–223. [Google Scholar]
- Fryer, J.G.; Brown, D.C. Lens distortion for close-range photogrammetry. Photogramm. Eng. Remote Sens. 1986, 52, 51–58. [Google Scholar]
- Kong, B. A Simple and Precise Method for Radial Distortion Calibration. J. Image Graph. 2004, 9. [Google Scholar] [CrossRef]
- Fraser, C.S. Digital camera self-calibration. Isprs J. Photogramm. Remote Sens. 1997, 52, 149–159. [Google Scholar] [CrossRef]
- Landsat Data Access|Landsat Missions. Available online: https://landsat.usgs.gov/landsat-data-access (accessed on 16 December 2018).
- CGIAR-CSI SRTM—SRTM 90m DEM Digital Elevation Database. Available online: http://srtm.csi.cgiar.org/ (accessed on 16 December 2018).
- Leprince, S.; Barbot, S.; Ayoub, F.; Avouac, J.-P. Automatic and precise orthorectification, coregistration, and subpixel correlation of satellite images, application to ground deformation measurements. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1529–1558. [Google Scholar] [CrossRef]
- Jiang, Y.; Cui, Z.; Zhang, G.; Wang, J.; Xu, M.; Zhao, Y.; Xu, Y. CCD distortion calibration without accurate ground control data for pushbroom satellites. Isprs J. Photogramm. Remote Sens. 2018, 142, 21–26. [Google Scholar] [CrossRef]
- Jiang, Y.-H.; Zhang, G.; Tang, X.; Li, D.; Huang, W.-C. Detection and Correction of Relative Attitude Errors for ZY1-02C. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7674–7683. [Google Scholar] [CrossRef]
- Xinming, T.; Guo, Z.; Huang, W.; Jiang, W.; Wu, X.; Fen, H. Plane and Stereo Precision Prediction Method for LEO Satellites. Available online: https://patents.google.com/patent/CN103868531A/zh (accessed on 16 December 2018).
- Wang, J.; Wang, R.; Xin, H.U. Discussion on Evaluation of Satellite Imagery Location Accuracy. Spacecr. Recov. Remote Sens. 2017, 38, 1–5. [Google Scholar]















| Satellite Platform | Total Satellite Mass | 19.8 Kg |
| Orbit height | 645 km | |
| Orbit inclination angle | 98° | |
| Regression cycle | 3–5 days | |
| Global Positioning System (GPS) positioning precision | uniaxial < 10 m (1σ) | |
| Attitude accuracy | ≤0.05° | |
| Attitude maneuver | Pitch axis > 0.9°/s | |
| Attitude stability | ≤0.004 °/s (1σ) | |
| Nightlight Sensor | Detector size | 11 um × 11 um |
| Field of View (FOV) | ≥32.32° | |
| Spectral range | 460–980 nm | |
| Quantization bits | 12 bit, processing to 15 bit @ HDR mode | |
| Band number | 1 | |
| Signal-to-noise ratio (SNR) | ≥35 dB | |
| Ground sample distance | 129 m @ 645 km | |
| Ground Swath | 264 km × 264 km @ 645 km |
| Parameters | Daytime | Nighttime |
|---|---|---|
| Exposure times (ms) | 0.049 | 17.089 |
| Frame period (s) | 0.1 | 5 |
| N | 1 | 7 |
| ID | Frame Number | Roll | Pitch | Yaw | Imaging Time | Imaging Mode | FP |
|---|---|---|---|---|---|---|---|
| England | 540 | 1.06° | −12.62° | 5.42° | 2018-06-28 | daytime | 0.1 s |
| Mexico | 39 | 3.97° | 1.17° | 3.36° | 2018-06-07 | daytime | 0.1 s |
| Caracas | 75 | 3.94° | 0.92° | 1.48° | 2018-06-10 | daytime | 0.1 s |
| Damascus | 79 | 5.33° | 0.26° | 1.63° | 2018-07-11 | daytime | 0.1 s |
| Korean | 8 | 18.02° | 0.96° | 0.22° | 2018-06-18 | nighttime | 5 s |
| 9 | 18.02° | 0.96° | 0.21° | 5 s | |||
| 10 | 17.98° | 0.97° | 0.18° | 5 s | |||
| 11 | 17.99° | 0.96° | 0.18° | 5 s | |||
| 12 | 18.07° | 0.96° | 0.16° | 5 s | |||
| Shanghai | 8 | 14.42° | 1.02° | −1.32° | 2018-07-14 | nighttime | 5 s |
| 9 | 14.39° | 1.01° | −1.32° | 5 s | |||
| 10 | 14.36° | 1.00° | −1.31° | 5 s | |||
| 11 | 14.36° | 0.98° | −1.33° | 5 s | |||
| 12 | 14.37° | 0.97° | −1.34° | 5 s |
| Calibration Scene | Across the Track (pixel) | Along the Track (pixel) | Plane Precision (pixel) | |||||
|---|---|---|---|---|---|---|---|---|
| MAX | MIN | RMS | MAX | MIN | RMS | |||
| England 2018.6.28 | A | 35.42 | 24.35 | 31.21 | 83.68 | 71.63 | 75.63 | 81.81 |
| B | 4.15 | 0.00 | 1.35 | 3.50 | 0.00 | 1.11 | 1.75 | |
| C | 0.30 | 0.00 | 0.13 | 0.46 | 0.00 | 0.15 | 0.20 | |
| Accuracy without GCPs | MAX (m) | MIN (m) | AVG (m) | RMS (m) |
|---|---|---|---|---|
| 1275 | 122 | 516.61 | 281.77 | |
| ID | Imaging time | Imaging location | Geometric accuracy without GCPs (m) | |
| 1 | 2018/6/4 1:12:15 | New Delhi, India | 309 | |
| 2 | 2018/6/4 2:48:41 | Abu Dhabi | 619 | |
| 3 | 2018/6/5 3:15:33 | Baghdad, Iraq | 395 | |
| 4 | 2018/6/6 11:45:02 | Atlanta | 798 | |
| 5 | 2018/6/13 21:45:02 | Wuhan, China | 592 | |
| 6 | 2018/6/13 19:38:49 | Crimea | 776 | |
| 7 | 2018/6/14 13:29:09 | East Korea | 840 | |
| 8 | 2018/6/16 22:14:16 | Shanghai, China | 404 | |
| 9 | 2018/6/18 21:27:09 | Korea | 222 | |
| 10 | 2018/6/20 6:00:45 | Barcelona | 473 | |
| 11 | 2018/6/21 3:09:23 | Moscow | 399 | |
| 12 | 2018/6/21 4:46:02 | Central Europe | 219 | |
| 13 | 2018/6/23 5:33:33 | France | 269 | |
| 14 | 2018/6/24 4:19:33 | Budapest | 570 | |
| 15 | 2018/6/30 5:05:33 | Rome | 1138 | |
| 16 | 2018/7/11 11:05:33 | Washington | 286 | |
| 17 | 2018/7/14 4:07:23 | Egypt | 212 | |
| 18 | 2018/7/14 22:00:33 | Shanghai, China | 222 | |
| 19 | 2018/7/15 22:23:43 | Fujian, China | 289 | |
| 20 | 2018/7/17 23:10:33 | Guiyang, China | 273 | |
| 21 | 2018/7/23 14:13:43 | San Francisco | 340 | |
| 22 | 2018/7/28 3:09:39 | Baghdad | 1085 | |
| 23 | 2018/7/31 22:14:33 | Zhangjiakou, China | 409 | |
| 24 | 2018/8/1 4:49:43 | Denmark Sweden | 234 | |
| 25 | 2018/8/1 6:22:23 | Madrid, Spain | 672 | |
| 26 | 2018/8/2 3:38:34 | Finland Sweden | 323 | |
| 27 | 2018/8/3 5:35:23 | Switzerland | 824 | |
| 28 | 2018/8/6 21:24:43 | Tokyo, Japan | 760 | |
| 29 | 2018/8/15 0:17:53 | Kazakhstan | 229 | |
| 30 | 2018/8/15 21:45:13 | Korean Peninsula | 741 | |
| 31 | 2018/8/16 1:00:53 | Xinjiang, China | 404 | |
| 32 | 2018/8/16 23:46:23 | Xinjiang, China | 122 | |
| 33 | 2018/8/17 4:40:03 | Athens, Greece | 446 | |
| 34 | 2018/8/18 0:08:53 | Xinjiang, China | 461 | |
| 35 | 2018/8/18 22:53:13 | Guilin, China | 211 | |
| 36 | 2018/8/19 23:16:03 | Chengdu, China | 235 | |
| 37 | 2018/8/20 13:58:13 | Vancouver | 617 | |
| 38 | 2018/8/20 22:04:23 | Zhejiang, China | 774 | |
| 39 | 2018/8/21 4:37:13 | Poland | 596 | |
| 40 | 2018/8/21 20:52:43 | Tokyo | 1057 | |
| 41 | 2018/8/21 22:27:33 | Nanchang, China | 1275 | |
| 42 | 2018/8/22 21:19:03 | Dalian, China | 313 | |
| 43 | 2018/8/22 22:50:53 | Guilin, China | 632 | |
| 44 | 2018/8/23 23:14:13 | Jinchang, China | 666 | |
| Verification Scene | Across the Track (pixel) | Along the Track (pixel) | Plane Precision (pixel) | |||||
|---|---|---|---|---|---|---|---|---|
| MAX | MIN | RMS | MAX | MIN | RMS | |||
| Mexico 2018.06.07 | D | 32.58 | 21.15 | 27.56 | 84.49 | 73.16 | 77.84 | 82.57 |
| E | 3.68 | 2.46 | 3.07 | 2.64 | 1.20 | 1.78 | 3.55 | |
| F | 4.27 | 0.00 | 1.11 | 3.57 | 0.00 | 1.04 | 1.52 | |
| G | 0.35 | 0.00 | 0.13 | 0.43 | 0.00 | 0.12 | 0.18 | |
| Caracas 2018.06.10 | D | 33.29 | 21.72 | 27.91 | 84.63 | 72.55 | 77.42 | 82.30 |
| E | 3.99 | 2.20 | 3.03 | 1.57 | 0.58 | 1.08 | 3.22 | |
| F | 4.23 | 0.00 | 1.20 | 3.47 | 0.00 | 0.96 | 1.54 | |
| G | 0.84 | 0.00 | 0.21 | 0.64 | 0.00 | 0.16 | 0.26 | |
| Damascus 2018.07.11 | D | 39.09 | 27.58 | 33.69 | 82.59 | 71.61 | 76.40 | 83.50 |
| E | 4.01 | 2.31 | 3.31 | 1.00 | 0.00 | 0.18 | 3.31 | |
| F | 4.55 | 0.00 | 1.07 | 4.17 | 0.00 | 0.89 | 1.39 | |
| G | 0.44 | 0.00 | 0.13 | 0.59 | 0.00 | 0.14 | 0.19 | |
| Verification Scene | Across the Track (pixel) | Along the Track (pixel) | Plane Precision (pixel) | |||||
|---|---|---|---|---|---|---|---|---|
| MAX | MIN | RMS | MAX | MIN | RMS | |||
| Mexico 2018.06.07 | D | 32.58 | 21.15 | 27.56 | 84.49 | 73.16 | 77.84 | 82.57 |
| E | 3.68 | 2.46 | 3.07 | 2.64 | 1.20 | 1.78 | 3.55 | |
| F | 4.27 | 0.00 | 1.11 | 3.57 | 0.00 | 1.04 | 1.52 | |
| G | 0.35 | 0.00 | 0.13 | 0.43 | 0.00 | 0.12 | 0.18 | |
| Caracas 2018.06.10 | D | 33.29 | 21.72 | 27.91 | 84.63 | 72.55 | 77.42 | 82.30 |
| E | 3.99 | 2.20 | 3.03 | 1.57 | 0.58 | 1.08 | 3.22 | |
| F | 4.23 | 0.00 | 1.20 | 3.47 | 0.00 | 0.96 | 1.54 | |
| G | 0.84 | 0.00 | 0.21 | 0.64 | 0.00 | 0.16 | 0.26 | |
| Damascus 2018.07.11 | D | 39.09 | 27.58 | 33.69 | 82.59 | 71.61 | 76.40 | 83.50 |
| E | 4.01 | 2.31 | 3.31 | 1.00 | 0.00 | 0.18 | 3.31 | |
| F | 4.55 | 0.00 | 1.07 | 4.17 | 0.00 | 0.89 | 1.39 | |
| G | 0.44 | 0.00 | 0.13 | 0.59 | 0.00 | 0.14 | 0.19 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Wang, J.; Jiang, Y.; Zhou, P.; Zhao, Y.; Xu, Y. On-Orbit Geometric Calibration and Validation of Luojia 1-01 Night-Light Satellite. Remote Sens. 2019, 11, 264. https://doi.org/10.3390/rs11030264
Zhang G, Wang J, Jiang Y, Zhou P, Zhao Y, Xu Y. On-Orbit Geometric Calibration and Validation of Luojia 1-01 Night-Light Satellite. Remote Sensing. 2019; 11(3):264. https://doi.org/10.3390/rs11030264
Chicago/Turabian StyleZhang, Guo, Jingyin Wang, Yonghua Jiang, Ping Zhou, Yanbin Zhao, and Yi Xu. 2019. "On-Orbit Geometric Calibration and Validation of Luojia 1-01 Night-Light Satellite" Remote Sensing 11, no. 3: 264. https://doi.org/10.3390/rs11030264
APA StyleZhang, G., Wang, J., Jiang, Y., Zhou, P., Zhao, Y., & Xu, Y. (2019). On-Orbit Geometric Calibration and Validation of Luojia 1-01 Night-Light Satellite. Remote Sensing, 11(3), 264. https://doi.org/10.3390/rs11030264