Statistical Properties of an Unassisted Image Quality Index for SAR Imagery
Abstract
:1. Introduction
[…] to quantitatively evaluate the results obtained using these new filters, with respect to classical ones, a Monte Carlo extension of Lee’s protocol is proposed. This extension of the protocol shows that its original version leads to inconsistencies that hamper its use as a general procedure for filter assessment.
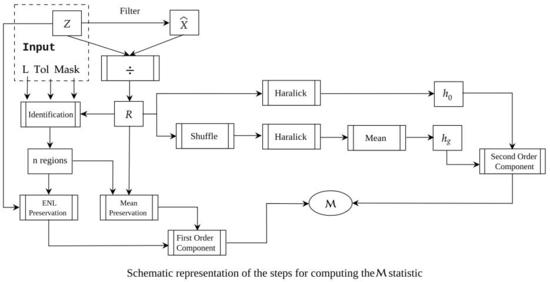
- First Order:
- which quantifies deviations from the hypothesis of observing identically distributed deviates from Gamma random variables with unitary mean and same shape parameter, and
- Second Order:
- which assesses departures from the independence hypothesis by quantifying the residual geometric content within the ratio image.
2. The Estimator
- : the homogeneity of the original ratio image R, and
- : the mean homogeneity calculated over 10 randomly shuffled versions of R.
3. The Distribution of
- Simulated SAR dataFigure 5 shows the two cases here considered: ramp and step, and an example of their speckled versions in the worst case: one look. The images are are pixels.
- Parameters
- -
- ENL: We chose two values for the number of looks: 1 (the worst case) and 4. From the authors’ experience, these two cases are enough for a sound Monte Carlo analysis.
- -
- Tolerance: Tolerance (Tol in Figure 4) refers to the relative deviation from the nominal and estimated values of ENL and the mean, as measured within the observed data in an textureless area. That is, an image region is considered textureless with a tolerance value of, for instance, 5% if its number of looks is, for instance, and the mean value is , and the measured and the measured . As above, two values for the tolerance have been set: 5% and 10%.
- -
- Window Mask: Window mask (Mask in Figure 4) is the size of the window used to measure ENL and . Two values have been set: and .
- Despeckling filters: As mentioned above, the despeckling filters used are the same employed in [37]. They are well-known and with proven efficiency. It is interesting to remark that the four filters are adaptive although conceptually different.
- -
- -
- SRAD: The Speckle Reducing Anisotropic Diffusion [17] filter belongs to the category of PDE-based (Partial Differential Equations) filters. As a difference with the rest of the filters used in this work, SRAD processes the whole image at once, that is, it is not based on convolution masks.
- -
- PPB: The Probabilistic Patch Based [10] is a nonlocal filter. This filter performs well on images corrupted with both additive and multiplicative noise.
- -
- FANS: The Fast Adaptive Nonlocal SAR [16] filter may be considered state-of-the art among despeckling filters since it provides outstanding results in most cases. FANS employs a set of wavelet transforms in a collaborative fashion with relative low computational cost.
4. Parametric Distribution Analysis
- Experiment 1. Simulation of under to evaluate its distribution under the null hypothesis (baseline), i.e., without applying any filter.
- Experiment 2. Simulation of step images, filtering, and then assessing .
- Experiment 3. Simulation of ramp images, filtering, and then assessing .
5. Experimental Results
5.1. Experiment 1
- mean and median are very close, if not identical; this suggests there are no one-sided outliers;
- Tolerance and Mask have less influence on the mean than ENL;
- although systematically positive, the skewness is small;
- kurtosis fluctuates around 3, the value for the Normal distribution, and remains relatively close to it.
5.2. Experiment 2
5.3. Experiment 3
- , ,
- , ,
- , ,
- , ,
- , ,
- , .
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
- , .
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A Tutorial on Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Goodman, J.W. Some fundamental properties of speckle. J. Opt. Soc. Am. 1976, 66, 1145–1150. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical properties of laser speckle patterns. In Laser Speckle and Related Phenomena; Dainty, J.C., Ed.; Springer: Berlin, Germany, 1982; Chapter 2; pp. 9–74. [Google Scholar]
- Lee, J.S. Digital image enhancement and noise filtering by use of local statistics. IEEE Trans. Pattern Anal. Mach. Intell. 1980, 2, 165–168. [Google Scholar] [CrossRef] [PubMed]
- Frost, V.S.; Stiles, J.A.; Shanmugan, K.; Holtzman, J. A model for radar images and its application to adaptive digital filtering of multiplicative noise. IEEE Trans. Pattern Anal. Mach. Intell. 1982, PAMI-4, 157–165. [Google Scholar] [CrossRef]
- Kuan, D.T.; Sawchuk, A.A.; Strand, T.C.; Chavel, P. Adaptive Noise Smoothing Filter for Images with Signal-Dependent Noise. IEEE Trans. Pattern Anal. Mach. Intell. 1985, PAMI-7, 165–177. [Google Scholar] [CrossRef]
- Lee, J.S.; Wen, J.H.; Ainsworth, T.L.; Chen, K.; Chen, A.J. Improved sigma filter for speckle filtering of SAR imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 202–213. [Google Scholar]
- Lopes, A.; Nezry, E.; Touzi, R.; Lau, H. Structure detection and statistical adaptive speckle filtering in SAR images. Int. J. Remote Sens. 1993, 14, 1735–1758. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Xi, C.; Guo, Y.; Peng, Q. A robust and fast non-local means algorithm for image denoising. In Proceedings of the IEEE International Conference on Computer-Aided Design and Computer Graphics, Beijing, China, 15–18 October 2007; p. 30. [Google Scholar]
- Deledalle, C.A.; Denis, F.; Tupin, F. Iterative weighted maximum likelihood denoising with probabilistic patch-based weights. IEEE Trans. Image Process. 2009, 18, 2661–2672. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.; Li, Y.; Jiao, L. SAR image despeckling using Bayesian nonlocal means filter with sigma preselection. IEEE Geosci. Remote Sens. Lett. 2011, 8, 809–813. [Google Scholar] [CrossRef]
- Sveinsson, J.R. Combined wavelet and curvelet denoising of SAR images using TV segmentation. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS’07), Barcelona, Spain, 23–28 July 2007; pp. 503–506. [Google Scholar]
- Schmitt, A.; Wessel, B.; Roth, A. Curvelet approach for SAR image denoising, structure enhancement, and change detection. In Proceedings of the ISPRS, CMRT09, Paris, France, 3–4 September 2009; pp. 151–156. [Google Scholar]
- Argenti, F.; Bianchi, T.; Lapini, A.; Alparone, L. Fast MAP despeckling based on Laplacian-Gaussian modeling wavelet coefficients. IEEE Geosci. Remote Sens. Lett. 2012, 9, 13–17. [Google Scholar] [CrossRef]
- Parrilli, S.; Poderico, M.; Angelino, C.V.; Verdoliva, L. A nonlocal SAR image denoising algorithm based on LLMMSE wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2012, 50, 606–616. [Google Scholar] [CrossRef]
- Cozzolino, D.; Parrilli, S.; Scarpa, G.; Poggi, G.; Verdoliva, L. Fast adaptive nonlocal SAR despeckling. IEEE Geosci. Remote Sens. Lett. 2014, 11, 524–528. [Google Scholar] [CrossRef]
- Yu, Y.; Acton, S.T. Speckle reducing anisotropic diffusion. IEEE Trans. Image Process. 2002, 11, 1260–1270. [Google Scholar] [PubMed]
- Zhao, Y.; Liu, J.G.; Zhang, B.; Hong, W.; Wu, Y. Adaptive total variation regularization based SAR image despeckling and despeckling evaluation index. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2765–2774. [Google Scholar] [CrossRef]
- Soccorsi, M.; Gleich, D.; Datcu, M. Huber-Markov model for complex SAR image restoration. IEEE Geosci. Remote Sens. Lett. 2010, 7, 63–67. [Google Scholar] [CrossRef]
- Li, Y.; Gong, H.; Feng, D.; Zhang, Y. An adaptive method of speckle reduction and feature enhancement for SAR images based on curvelet transform and particle swarm optimization. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3105–3116. [Google Scholar] [CrossRef]
- Gomez, L.; Munteanu, C.; Buemi, M.; Jacobo-Berlles, J.; Mejail, M. Supervised constrained optimization of Bayesian nonlocal means filter with sigma preselection for despeckling SAR images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4563–4575. [Google Scholar] [CrossRef]
- Scarnati, T.; Gelb, A. Variance based joint sparsity reconstruction of synthetic aperture radar data for speckle reduction. Proc. SPIE 2019, 10647R, 1–14. [Google Scholar] [CrossRef]
- Argenti, F.; Lapini, A.; Bianchi, T.; Alparone, L. A Tutorial on Speckle Reduction in Synthetic Aperture Radar Images. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–35. [Google Scholar] [CrossRef]
- Li, F.; Shen, C.; Fan, J.; Shen, C. Image restoration combining a total variational filter and a fourth-order filter. J. Vis. Commun. Image Represent. 2007, 18, 322–330. [Google Scholar] [CrossRef]
- Liu, G.; Huang, T.; Liu, J. Hig-order TVL1-based images restoration and spatially adapted regularization parameter selection. Comput. Math. Appl. 2014, 67, 2015–2026. [Google Scholar] [CrossRef]
- Xu, J.; Feng, A.; Hao, Y.; Zhang, X.; Han, Y. Image deblurring and denoising by an improved variational model. Int. J. Electron. Commun. 2016, 70, 1128–1133. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Jin, W.; Zhang, Y. A new alternating minimization algorithm for total variation image reconstruction. SIAM J. Imaging Sci. 2008, 1, 248–272. [Google Scholar] [CrossRef]
- Lee, J.S.; Jurkevich, I.; Dewaele, P.; Wambacq, P.; Oosterlinck, A. Speckle filtering of synthetic aperture radar images: A review. Remote Sens. Rev. 1994, 8, 313–340. [Google Scholar] [CrossRef]
- Gomez, L.; Buemi, M.E.; Jacobo-Berlles, J.; Mejail, M. A new image quality index for objectively evaluating despeckling filtering in SAR images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 297–1307. [Google Scholar] [CrossRef]
- Torres, L.; Sant’Anna, S.; Freitas, C.; Frery, A.C. Speckle reduction in polarimetric SAR imagery with stochastic distances and nonlocal means. Pattern Recognit. 2014, 47, 141–157. [Google Scholar] [CrossRef]
- Moschetti, E.; Palacio, M.G.; Picco, M.; Bustos, O.H.; Frery, A.C. On the use of Lee’s protocol for speckle-reducing techniques. Lat. Am. Appl. Res. 2006, 36, 115–121. [Google Scholar]
- Shen, P.; Wang, C.; Gao, H.; Zhu, J. An Adaptive Nonlocal Mean Filter for PolSAR Data with Shape-Adaptive Patches Matching. Sensors 2018, 18, 2215. [Google Scholar] [CrossRef]
- Lang, F.; Yang, J.; Li, D.; Shi, L.; Wei, J. Mean-shift-based speckle filtering of polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4440–4454. [Google Scholar] [CrossRef]
- Xu, B.; Cui, Y.; Zuo, B.; Yang, J.; Song, J. Polarimetric SAR image filtering based on path ordering and simultaneous sparse coding. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4079–4093. [Google Scholar] [CrossRef]
- Fenandez-Michelli, J.I.; Hurtado, M.; Areta, J.A.; Muravchik, C. Unsupervised polarimetric SAR image classification using G0 mixture model. IEEE Geosci. Remote Sens. Lett. 2017, 14, 754–758. [Google Scholar] [CrossRef]
- Xu, J.; Huang, Z.; Yan, L.; Zhou, X.; Zhang, F.; Long, T. SAR Ground Moving Target Indication Based on Relative Residue of DPCA Processing. Sensors 2016, 16, 1676. [Google Scholar] [CrossRef] [PubMed]
- Gomez, L.; Ospina, R.; Frery, A.C. Unassisted quantitative evaluation of despeckling filters. Remote Sens. 2017, 9, 389. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A review of image denoising algorithms, with a new one. Multiscale Model. Simul. 2005, 4, 490–530. [Google Scholar] [CrossRef]
- Achim, A.; Kuruoglu, E.; Zerubia, J. SAR image filtering based on the heavy-tailed Rayleigh model. IEEE Trans. Image Process. 2006, 15, 2686–2693. [Google Scholar] [CrossRef]
- Martino, G.D.; Poderico, M.; Poggi, G.; Riccio, D.; Verdoliva, L. Benchmarking framework for SAR despeckling. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1596–1615. [Google Scholar] [CrossRef]
- Vitale, S.; Cozzolino, D.; Scarpa, G.; Verdoliva, L.; Poggi, G. Guided patch-wise nonlocal SAR despeckling. arXiv, 2018; arXiv:1811.11872. [Google Scholar]
- McCullagh, P. What is a statistical model? Ann. Stat. 2002, 30, 1225–1267. [Google Scholar] [CrossRef]
- Thas, O. Comparing Distributions; Springer: Berlin, Germany, 2010. [Google Scholar]
- Cao, R.; Lugosi, G. Goodness-of-fit tests based on the kernel density estimator. Scand. J. Stat. 2005, 32, 599–616. [Google Scholar] [CrossRef]
- Wassermann, L. All of Nonparametric Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Lee, J.S. Speckle Suppression and Analysis for Synthetic Aperture Radar Images. Opt. Eng. 1986, 25, 636–643. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Runger, G.C.; Hubele, N.F. Engineering Statistics; John Wiley & Sons: New York, NY, USA, 2009. [Google Scholar]
- Arias-Castro, E.; Candès, E.J.; Plan, Y. Global testing under sparse alternatives: ANOVA, multiple comparisons and the higher criticism. Ann. Stat. 2011, 39, 2533–2556. [Google Scholar] [CrossRef]
- Yohai, V.J. High breakdown-point and high efficiency robust estimates for regression. Ann. Stat. 1987, 15, 642–656. [Google Scholar] [CrossRef]
- Silverman, B. Density Estimation London; Chapman and Hall: London, UK, 1986. [Google Scholar]
- Rupert, G., Jr. Simultaneous Statistical Inference; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Sheather, S.J.; Jones, M.C. A reliable data-based bandwidth selection method for kernel density estimation. J. R. Stat. Soc. Ser. B 1991, 53, 683–690. [Google Scholar] [CrossRef]
- Fan, J. Local Polynomial Modelling and Its Applications: Monographs on Statistics and Applied Probability 66; Routledge: London, UK, 2018. [Google Scholar]
- Kitchenham, B.; Madeyski, L.; Budgen, D.; Keung, J.; Brereton, P.; Charters, S.; Gibbs, S.; Pohthong, A. Robust statistical methods for empirical software engineering. Empir. Softw. Eng. 2017, 22, 579–630. [Google Scholar] [CrossRef]
- Razali, N.M.; Wah, Y.B. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Dwan, K.; Altman, D.G.; Arnaiz, J.A.; Bloom, J.; Chan, A.W.; Cronin, E.; Decullier, E.; Easterbrook, P.J.; Von Elm, E.; Gamble, C.; et al. Systematic Review of the Empirical Evidence of Study Publication Bias and Outcome Reporting Bias. PLoS ONE 2008, 3, e3081. [Google Scholar] [CrossRef] [PubMed]
- MATLAB. Version 8.3.0.532 (R2014a); The MathWorks Inc.: Natick, MA, USA, 2014. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Lehmann, E.L.; Romano, J.P. Testing Statistical Hypotheses; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]








| FANS | E-Lee () | E-Lee () | ||
|---|---|---|---|---|
| 3.7478 | 8.1648 | 20.2215 | 23.1691 |
| ENL | Tol. | Mask | |||||
|---|---|---|---|---|---|---|---|
| 1 | 5 | 15 | 0.0202 | 0.0201 | 0.00234 | 0.2411 | 2.80 |
| 1 | 10 | 15 | 0.0258 | 0.0258 | 0.00189 | 0.0953 | 3.31 |
| 4 | 5 | 15 | 0.0138 | 0.0138 | 0.00139 | 0.0421 | 2.77 |
| 4 | 10 | 15 | 0.0190 | 0.0189 | 0.00137 | 0.3043 | 3.36 |
| 1 | 5 | 25 | 0.0145 | 0.0145 | 0.00204 | 0.4129 | 3.90 |
| 1 | 10 | 25 | 0.0191 | 0.0191 | 0.00197 | 0.2558 | 3.06 |
| 4 | 5 | 25 | 0.0107 | 0.0105 | 0.00147 | 0.3648 | 2.76 |
| 4 | 10 | 25 | 0.0147 | 0.0145 | 0.00182 | 0.1756 | 2.50 |
| ENL | Tol | Mask | |||
|---|---|---|---|---|---|
| 1 | 5 | 15 | 0.0243 | 0.0250 | 0.0261 |
| 1 | 10 | 15 | 0.0291 | 0.0299 | 0.0314 |
| 4 | 5 | 15 | 0.0161 | 0.0163 | 0.0174 |
| 4 | 10 | 15 | 0.0214 | 0.0226 | 0.0230 |
| 1 | 5 | 25 | 0.0177 | 0.0204 | 0.0212 |
| 1 | 10 | 25 | 0.0224 | 0.0239 | 0.0245 |
| 4 | 5 | 25 | 0.0132 | 0.0142 | 0.0142 |
| 4 | 10 | 25 | 0.0178 | 0.0186 | 0.0189 |
| Experiment | Model Statistics | p-Value | VAC (%) | |
|---|---|---|---|---|
| 1 | ENL model | 286.54 | 29.18 | |
| 373.57 | 52.60 | |||
| 1044.44 | 68.95 | |||
| 2 | ENL model | 3088.69 | 36.32 | |
| 1133.47 | 40.91 | |||
| 433.47 | 61.36 | |||
| 4.50 | 0.03 | 61.42 | ||
| 3 | ENL model | 2423.97 | 28.77 | |
| 349.30 | 34.28 | |||
| 1831.98 | 54.98 | |||
| 15.67 | 55.09 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez, L.; Ospina, R.; Frery, A.C. Statistical Properties of an Unassisted Image Quality Index for SAR Imagery. Remote Sens. 2019, 11, 385. https://doi.org/10.3390/rs11040385
Gomez L, Ospina R, Frery AC. Statistical Properties of an Unassisted Image Quality Index for SAR Imagery. Remote Sensing. 2019; 11(4):385. https://doi.org/10.3390/rs11040385
Chicago/Turabian StyleGomez, Luis, Raydonal Ospina, and Alejandro C. Frery. 2019. "Statistical Properties of an Unassisted Image Quality Index for SAR Imagery" Remote Sensing 11, no. 4: 385. https://doi.org/10.3390/rs11040385
APA StyleGomez, L., Ospina, R., & Frery, A. C. (2019). Statistical Properties of an Unassisted Image Quality Index for SAR Imagery. Remote Sensing, 11(4), 385. https://doi.org/10.3390/rs11040385