Spectral Heterogeneity Predicts Local-Scale Gamma and Beta Diversity of Mesic Grasslands

Abstract

Plant species diversity is an important metric of ecosystem functioning, but field assessments of diversity are constrained in number and spatial extent by labor and other expenses. We tested the utility of using spatial heterogeneity in the remotely-sensed reflectance spectrum of grassland canopies to model both spatial turnover in species composition and abundances (β diversity) and species diversity at aggregate spatial scales (γ diversity). Shannon indices of γ and β diversity were calculated from field measurements of the number and relative abundances of plant species at each of two spatial grains (0.45 m² and 35.2 m²) in mesic grasslands in central Texas, USA. Spectral signatures of reflected radiation at each grain were measured from ground-level or an unmanned aerial vehicle (UAV). Partial least squares regression (PLSR) models explained 59–85% of variance in γ diversity and 68–79% of variance in β diversity using spatial heterogeneity in canopy optical properties. Variation in both γ and β diversity were associated most strongly with heterogeneity in reflectance in blue (350–370 nm), red (660–770 nm), and near infrared (810–1050 nm) wavebands. Modeled diversity was more sensitive by a factor of three to a given level of spectral heterogeneity when derived from data collected at the small than larger spatial grain. As estimated from calibrated PLSR models, β diversity was greater, but γ diversity was smaller for restored grassland on a lowland clay than upland silty clay soil. Both γ and β diversity of grassland can be modeled by using spatial heterogeneity in vegetation optical properties provided that the grain of reflectance measurements is conserved.

1. Introduction

Grasslands cover ~25% of terrestrial area [1] and support multiple products and services, including livestock and wildlife production, and a diverse array of plants, animals, birds, and arthropods [2]. Primary productivity [3], temporal stability in productivity [3,4,5,6], and other ecosystem functions and services on grasslands are enhanced by high levels of plant species diversity, as influenced by both species richness and evenness, including diversity at multiple spatial scales [7,8,9]. For example, increasing species diversity at both local (α diversity) and larger spatial scales (γ diversity) improved multiple grassland functions, whereas increasing diversity differences among local communities (β diversity) increased functional reliability at larger spatial scales [8].

Increased recognition of the importance of plant diversity to ecosystem functions has incentivized efforts to develop remote sensing techniques to estimate diversity. Field-based measurements of diversity are expensive, labor-intensive, and typically limited in spatial extent. Airborne remote sensing, by contrast, could provide rapid, cost-efficient assessments of diversity at the multiple spatial scales relevant to management and conservation [10]. Indeed, taxonomic diversity may be regarded as an ‘essential biodiversity variable’, the measurement of which is required to effectively monitor, report, and manage biodiversity change [11,12]. Most remote sensing products for species richness and γ and α diversity estimation derive from the premise that diversity is correlated to spatial variation in the reflectance spectrum (optical diversity in space or spectral heterogeneity [10,13,14]). Wang et al. [13], for example, demonstrated that the Shannon Index of species diversity was strongly correlated with an optical index derived by averaging the coefficient of variation (CV) of spectral reflectance in space across measured wavebands. On the other hand, diversity at small spatial scales (several m²) can be detected by using among-waveband differences in reflectance, rather than spatial variation in reflectance, provided that optical properties of species or functional groups are well-differentiated in the reflectance signal [15,16,17].

More complex techniques often are employed to link remote sensing signals to β diversity, defined generally as spatial turnover of species [18]. Methods that employ spectral distances or differences are required to explain ‘differences’ in diversity among communities (one metric of β diversity; [18,19,20]). Dalmayne et al. [21], for example, demonstrated that spectral dissimilarity and species compositional dissimilarity were correlated when compared between grassland plots at small spatial scales (2 m × 2 m). Simpler techniques, such as those based on spectral dispersion, including the CV in reflectance among plant communities, may yield a correlation with β diversity measured as variation in species composition and relative abundances among communities. We anticipate that compositional variance among a set of vegetation samples is correlated with the sum of squares of species relative abundances among samples, which in turn likely will correlate with statistically-related measures of spatial variation (e.g., the CV) in the reflectance spectrum.

The relationship between spatial variation in canopy optical properties and species diversity often is assumed to be indirect, the result of soil or disturbance effects on canopy structure and chemistry that are in turn linked to variation in diversity (e.g., [21]). An alternative explanation is that spatial heterogeneity in canopy optical properties results largely from differences in structural or functional properties of species themselves.

In the present study, we used hyperspectral measurements from ground-based and airborne platforms to model γ and β diversity of composites of vegetated scenes sampled at each of two spatial scales [grain or spatial resolution = plot (0.43 m²) and patch scales (35.2 m²)] in mesic grasslands that differ in management. Spatial scale is widely recognized to influence relationships between vegetation parameters and the reflectance spectrum [13]. Specific objectives were to: (1) develop a statistical model for grassland diversity (γ and β diversity) applicable at the field/local scale, (2) assess the influence of the spatial scale of reflectance measurements on modeled diversity, and (3) apply statistical models to estimate diversity in restored grassland.

2. Materials and Methods

We measured species diversity and spectral reflectance of plant communities in three contiguous fields located in Temple, Texas, USA (31°10′N, 97°34′W; Figure 1. Sampled fields included a pasture dominated by introduced (exotic) C₄ perennial grasses, principally Bothriochoa ischaemum (L.) Keng and Cynodon dactylon (L.) Pers.; a remnant (never-plowed) tallgrass prairie; and a former agricultural field planted with stands of either a mixture of native perennial forb and grass species (restored grassland) or a monoculture of the native C₄ grass Panicum virgatum L. (cultivar ‘Alamo’). Stands in the former agricultural field (long-term biomass experiment (LTBE)) are 17 m wide and 137 to 218 m long (0.26–0.37 hectares) and traverse a catena from a silty clay soil on the upland (Austin series; 43% clay, 1.1% organic C to 50 cm depth) to a clay soil on the lowland (Houston Black series; 52% clay, 1.7% organic C to 50 cm depth) [22]. Eight randomly-selected stands of the total of 24 stands in LTBE were planted with a mixture of perennial grassland species in 2010. Remaining stands were planted with P. virgatum. In each stand of restored grassland with mixed-species, we permanently located 13 patches each 7 m in diameter along the upland to lowland catena, for a total of 52 patches per soil type. We also randomly located eight, 7 m diameter patches in the pasture and six patches in the smaller native prairie. Sampled grasslands are not grazed by domestic livestock, but are hayed annually, the pasture in June and prairie and restored grassland following the growing season. All grasslands were sampled prior to any major disturbance to canopy structure.

We visually quantified cover by species and cover of bare soil in eight randomly-chosen patches on each soil type in LTBE during both April–May and August 2017 (n = 32) and in each patch in the pasture (n = 8) and native prairie during April–May 2018 (n = 6). Cover per patch was estimated by measuring cover of bare soil and by species in each of eight randomly-located plots (76 cm diameter) in each patch. Within one week of quantifying species cover, we measured the spectral signature of reflected radiation from each 76 cm diameter plot and each 7 m diameter patch in each field using an ASD HandHeld2 Pro spectroradiometer (spectral range of 350–1070 nm; ASD Inc., Boulder, CO, USA). Reflectance was calculated as the ratio of radiance reflected from the plant canopy to radiance incident on the canopy, the latter measured as the radiant flux reflected from a Spectralon^® white reference panel exposed to full sunlight. In practice, the electrical current from photodetectors in the HandHeld 2 is converted to a computer digital number (DN). Reflectance is calculated as the ratio of the DN resulting from energy reflected from the canopy to the DN of energy incident on the canopy. Reflectance was measured from directly above each plot at 1.71 m height (10° field of view) and each patch at 15.8 m height (25° field of view), the latter using an unmanned aerial vehicle (UAV) (S1000; DJI; Shenzhen, China) equipped with the ASD HandHeld2 sensor. Patch reflectance was measured by flying the GPS-guided, rotary-wing UAV to a stationary position above each patch. Reflectance per patch in LTBE also was measured at approximately two week intervals during the 2016–2018 growing seasons (March-November). Reflectance was measured on cloudless days within 2 h of solar noon. All measurements were referenced to a Spectralon^® white reference panel at ~15 min intervals to maintain consistency in observations. From the reflectance spectrum, we calculated the normalized difference vegetation index (NDVI) for each plot and patch by dividing the difference in reflectance between near infrared and red wavebands by the sum of reflectance in near infrared and red bands.

We calculated species diversity as the exponential of Shannon entropy (Shannon diversity) for i = 1 to S species,

$$\mathrm{Diversity}=\exp (-{{\displaystyle \sum }}_{i=1}^{S}pi x ln pi)$$

(1)

where p_i = proportion of total plant cover for species i. Shannon diversity is interpreted as the number of equally-abundant species required to produce the calculated value of the index [23,24]. The exponential transformation converts Shannon entropy to its number equivalent, reflective of ‘true diversity’ [24]. We calculated species diversity for each 76 cm diameter plot (plot scale; 0.45 m²), each grouping of eight plots per patch, representative of diversity at the patch scale (35.2 m²), and for randomly-created groupings of between 4 and 40 of the total of 46 patches for which species data were available (community scale, e.g., each community was assembled by randomly selecting, without replacement, the desired number of patches from the total of 46 patches). From γ and mean α diversity at the patch and community scales, we calculated β diversity,

β = γ/α

(2)

where α is mean diversity across the plots or patches that were aggregated to represent patches and communities, respectively. β is an index of compositional similarity among plots or patches, interpreted as the effective number of completely distinct assemblages included in the sample [24]. Multiplicative β is not systematically correlated with (is unrelated to) γ or α, but is strongly influenced by the number of assemblages included in calculating γ (N; [24,25]). Following Chao et al. [25], we transformed β to unit interval (designated as β_0-1)

β_0-1 = (1/β − 1/N)/(1 − 1/N)

(3)

Transformation removed the logarithmic dependence of β on the number of assemblages analyzed in aggregate. β_0-1 is interpreted as the mean fraction of species shared among assemblages [25].

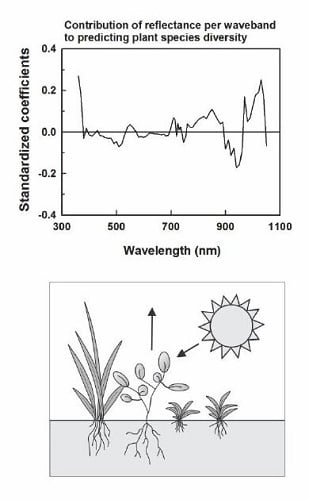
In seeking a statistical model for grassland diversity, we assumed that canopy-level reflectance in the visible and near infrared differs among species and species ‘functional’ types and, more generally, among vegetated scenes that differ in diversity. As a partial test of these assumptions, we compared reflectance vs. wavelength relationships among five groups of sampled species that differ in canopy structure, phenology, or leaf chemical and structural properties and between groups of patches that differed in mean diversity. Functional groups include C₄ perennial grasses (e.g., B. ischaemum, Bouteloua curtipendula (Michx.) Torr., Panicum coloratum L.), C₃ perennial grasses (e.g., Nassella leucotricha (Trin. & Rupr.) Barkworth), C₃ annual grasses (e.g., Bromus japonicus Thunb. Ex Murray), C₃ annual forbs (e.g., Gaillardia pulchella Foug), and C₃ perennial forbs (Helianthus maximiliani Schrad., Solidago canadensis L.). We identified plots in which each functional group contributed >50% of plant cover (n = 4–6 plots per group). For each function group, we then averaged reflectance per waveband across plots and graphed mean reflectance as a function of wavelength. We also compared reflectance vs. wavelength relationships between groups of 7 m diameter patches that differed in mean diversity. Reflectance per waveband was averaged across patches with γ diversity < 6.0 and > 6.0 (low and high diversity, respectively). Mean reflectance then was graphed as a function of wavelength for low and high diversity patches.

We used two modeling approaches to evaluate correlations between γ and β diversity and hyperspectral measurements of canopy reflectance. Both approaches are based on the premise that diversity of plot or patch aggregates is related to spatial heterogeneity (among-plot or among-patch differences) in reflectance along the visible to near infrared spectrum that we measured (spectral variance or heterogeneity approach). First, we evaluated the relationship between γ and β (β_0-1) diversity of aggregates of plots (patch scale) and patches (community scale) and ‘optical diversity’ [13]. Optical diversity was calculated by averaging the among-component (plot or patch) CV in reflectance at each waveband across all wavebands measured. Second, we used partial least squares regression (PLSR) analysis to model the diversity of plot and patch aggregates (patch and community scales, respectively) as a function of the among-plot or among-patch CV in reflectance at each waveband measured. PLSR models were developed using data from areas on which species diversity was measured. The diversity of patches was modeled using the CV in reflectance among the eight, 76 cm plots per patch on which species cover was measured. The diversity of communities was modeled using the CV in reflectance among the 7 m diameter patches that together formed the community. Communities were created by randomly selecting 4 (n = 16), 8 (n = 16), 16 (n = 8), 24 (n = 4), 32 (n = 2), and 40 (n = 1) patches from the total of 46 patches for which species diversity was measured (range in spatial scale = 154–1540 m²). Prior to PLSR analysis, we averaged reflectance measurements from each plot and patch over 5 nm wavebands, beginning at the 661–665 nm band and ending at 756–760 nm, and 10 nm wavebands over the remainder of the 350–1050 nm spectrum, resulting in a total of 80 wavebands. Data were retrieved in 1 nm wavebands, although the effective resolution of the ASD sensor is ~3 nm. Reflectance data were averaged to 5 to 10 nm waveband widths to stabilize readings and reduce the total number of wavebands considered. Smaller (5 nm) waveband widths were calculated from 661–760 nm to increase the relative representation of wavebands in which chlorophyll absorption typically is high. In doing so, we assumed that among plot or patch variation in leaf functioning, as reflected in chlorophyll absorption, would correlate with variation in species diversity. Reflectance data for the 80 wavebands per plot or patch were normalized to a uniform brightness of 1 (Brightness normalization; [26]). Brightness normalization has been shown to improve the stability of PLSR models by dampening effects of canopy shade on model fits [26].

PLSR reduces the number of predictive CV signals from that of all wavebands to a smaller set of uncorrelated latent variables [27]. The optimal number of latent variables required to predict γ or β diversity was determined by using a “split-sample” cross validation procedure [28]. A PLSR model was fit to a data set composed of CV values from every seventh plot or patch aggregate in the list of 46 and 47 plot and patch aggregates, respectively, beginning with the first entry in the list, while minimizing the prediction error for unfitted data. The process was repeated iteratively by beginning split-sample data sets with data from each successive entry in the list. We chose the PLSR model with >1 latent variable that produced the first minimum in residuals from predictions of unfitted data (root mean predicted residual sum of squares (PRESS)). We then tested the utility of PLSR models for γ and β_0-1 diversity that used fewer than the complete data set of 80 wavebands in prediction. Wavebands for which values of the variable importance in prediction (VIP) were < 0.8 were deleted iteratively to identify PLSR models with fewer wavebands. We used linear and non-linear (exponential; hyperbolic) regression analyses to describe relationships between cumulative γ diversity and the number of plots (each 0.45 m²) sampled in 7 m diameter patches. PLSR and linear/non-linear regressions were fit using SAS 9.4.

3. Results

3.1. Reflectance Patterns for Species Functional Groups

Reflectance diverged strongly among functional groups of species, particularly in red and near infrared wavebands (Figure 2). Reflectance in the far red plus near infrared (ca. 750–1050 nm) was least among C₃ annual and C₄ perennial grasses and highest among C₃ forb species, including both annual and perennial forbs. Reflectance in the red (ca. 550–650 nm) was lower among C₃ annual and perennial grasses then C₄ grasses. Perennial forbs were distinguished from annual forbs by lower reflectance in the red.

3.2. Diversity of Patches

Gamma diversity across the eight plots sampled per 7 m diameter patch (γ_patch) varied between 1 and 18.6 and was more highly correlated with variation in the mean α diversity of plots (adj. r² = 0.91) than with β diversity among plots (β_patch adj. r² = 0.39, n = 48; not shown). γ_patch was only weakly correlated with the mean CV in reflectance across wavebands (optical diversity; adj. r² = 0.12). β_patch was not correlated to optical diversity (P = 0.12). By contrast, variation in both γ_patch and β_patch were well described by a PLSR model using a data set that included the CV in reflectance among plots for each of 80 wavebands. PLSR accounted for 63% (eight latent variables; PRESS = 0.99) and 59% (5 latent variables; PRESS = 1.02; Figure 3) of variance in γ_patch when fit using the CV in non-transformed and normalized reflectance values, respectively.

A PLSR with 6 latent variables accounted for 68% of the variance in β_patch when fit using values of the CV of normalized reflectance values per waveband (PRESS = 1.04; Figure 3), but only 17% of variance in β_patch when fit using the CV of non-transformed reflectance values (not shown). Residuals from model fits to γ_patch and β_patch were not correlated with the mean or CV in either the NDVI or the percentage cover of bare soil among plots per patch (P = 0.07–0.79).

Variation in both γ_patch and β_patch were associated most strongly with the CV in reflectance in blue (360–390 nm), red (650–750 nm), and near infrared (890–1010 nm) wavebands as indicated by the large departures of standardized weightings of PLSR coefficients from the zero line over these spectral ranges (Figure 4). This pattern is consistent with differences in reflectance vs. waveband relationships observed between patches with high vs. lower diversity. Reflectance was smaller in blue and red wavebands and greater in the near infrared in patches with high than lower diversity (Figure S1).

We used γ diversity of the 8 plots sampled per patch as an estimate of α diversity at the patch scale. Values of among-plot γ approached saturation as the number of plots sampled per patch was increased from six to eight (Figure 5), implying that γ diversity of plot aggregates provided a reasonable estimate of diversity at the larger spatial scale of the 7 m diameter patch.

3.3. Diversity of Communities

Gamma diversity of communities consisting of random combinations of 4–40 patches (γ_com) varied between 10.2 and 36.4 and was positively correlated with variation in both the mean α and β diversity (β_com) of patch aggregates (adj. r² = 0.44 and 0.27, respectively; P < 0.0001, n = 47). As anticipated, transforming β_com to unit interval (β_0-1) eliminated (P = 0.32) the strong correlation between β_com and the number of patches that were combined to create communities [β_com = 1.135 + 0.90*ln(# patches), adj. r² = 0.82, P < 0.0001]. β_0-1 also was statistically independent of both γ_com (P = 0.32) and the mean α diversity of patch aggregates (P = 0.07).

Variation in both γ_com and β_0-1 were well described by a PLSR fit to the CV of normalized reflectance values among patches that together formed communities. PLSR accounted for 85% (seven latent variables; PRESS = 0.65) of variance in γ_com and 79% (eight latent variables; PRESS = 1.09) of variance in β_0-1 (Figure 6). By contrast, γ_com and β_0-1 were either not correlated or correlated only weakly with optical diversity (P = 0.57 and P = 0.01, adj. r² = 0.12, respectively).

As indicated by standardized weightings of PLSR coefficients, variation in both γ_com and β_0-1 was associated mainly with among-patch differences in reflectance in blue (350–370 nm) and near infrared wavebands (810–1050 nm; Figure 7). Variation in β_0-1 also depended strongly on the CV in reflectance in red wavebands (660–770 nm).

We tested for PLSR models that used fewer than the full set of 80 wavebands to predict γ_com and β_0-1 by iteratively eliminating wavebands for which VIP values were < 0.8 from the full model. PLSR explained 81% of the variance in γ_com (6 latent variables) after excluding green and most red wavebands (450–810 nm, 700 nm excepted; n = 21 wavebands modeled) and 82% of variance in β_0-1 (9 latent variables; n = 55 wavebands) after excluding wavebands in the green and lower red portions of the spectrum (480–650 nm).

PLSR estimates of diversity depended strongly on the spatial scale of the data used to develop predictive equations. Predicted values of the γ diversity of plot aggregates were greater than observed γ by a factor of three, on average, when estimated using a PLSR calibrated to relationships between diversity and reflectance at the spatial scale of patch aggregates (community). Sensitivity of diversity estimates to a given level of spectral variation was, therefore, much greater at the small than at the larger spatial scale.

3.4. Diversity of Restored Grassland

We used PLSR models fit to the CV in normalized reflectance values of all measured wavebands to estimate diversity during spring 2016–2018 on clay and silty clay soils in the LTBE (n = 52 patches per community). γ_com was smaller on the clay than silty clay soil by 1, 3, and 2 ‘effective’ species in 2016, 2017, and 2018, respectively, representing a decline in γ_com of 6–17% on the clay compared to silty clay soil (Figure 8). β_com (derived from modelled β_0-1), by contrast, was larger by about 0.4 species on the clay than silty clay soil across years. Because γ_com was smaller and β_com was slightly greater on the clay than silty clay, α was lower by 0.5–2.0 species on the clay than silty clay.

Soils differed in relative cover of annual species, but not in early-season biomass. Relative cover of annual species was significantly greater on the silty clay than clay soil in May 2017 (0.74 vs. 0.58; paired t-test, P = 0.01, df = 7). Conversely, NDVI during spring, a surrogate for early-season biomass, did not differ between soil types in any year (mean = 0.72, 0.64, 0.64 for 2016, 2017, and 2018, respectively).

4. Discussion

We modeled grassland γ and β diversity measured at two spatial grains using spatial variability in the reflectance spectrum. γ and β diversity of aggregates of scenes measured at each spatial grain were well described by a PLSR model using a data set that included 80 wavebands but were only weakly correlated to spatial variation in reflectance averaged across wavebands (optical diversity). Predicted diversity varied more per unit of difference in spectral heterogeneity at the large than smaller spatial grain, indicating that PLSR estimates of diversity were strongly scale-dependent. Diversity of restored grassland during spring was estimated from a calibrated PLSR model. Grassland communities on a heavy clay soil supported relatively fewer equally-common species but exhibited greater spatial turnover in species composition and abundances than did those on an upland, silty clay soil. Our results support the view that grassland diversity is correlated with spatial variability in canopy structure and function at small- to moderately-sized spatial grains (pixels) but, consistent with previous investigations (e.g., [10,17]), demonstrate that spectral models developed for a given spatial grain cannot reliably be applied to data collected at differing grains.

Several have confirmed the utility of PLSR for estimating species richness or diversity from remote sensing measurements (e.g., [15,16,21]). Our results demonstrate that both γ and β diversity can be modelled with high confidence by using spatial variation in spectral reflectance for each of multiple wavebands. PLSR explained >58% of variance in diversity. The standard errors of the estimate (SEE) of diversity predictions were small (SEE = 0.39 for α diversity; 0.03 and 0.004 for β diversity and β_0-1 of plot and patch assemblages, respectively). β diversity is particularly challenging to estimate from remote measurements [10]. But, like γ diversity, differences in species composition and relative abundances among communities (β diversity) varied as a function of spatial heterogeneity in canopy optical properties at the spatial grains that we considered. Multiplicative indices of β diversity have been criticized as scale dependent because values are influenced by both γ and α diversity [29]. The unit internal transformation of Shannon β that we used is not systematically correlated with either γ or α diversity [24]. Consequently, PLSR did not successfully model β diversity simply because the procedure also described variation in γ diversity. Shannon β also is strongly correlated with the number of assemblages included in calculations [24,25]. The unit internal transformation of Shannon β that we fit using PLSR is not biased by assemblage number.

We speculate that spatial variation in reflectance predicted species diversity because spatial differences in reflectance were associated with species differences in leaf function and canopy structure [13]. Results are consistent with this prediction. Reflectance signatures differed among functional groups of species and between patches that differed in mean diversity. Grasslands that we studied were not grazed or hayed during the growing season of sampling, thereby eliminating effects of large disturbances on canopy structure and likely enhancing contributions of species functional and structural differences to canopy optical heterogeneity. PLSR models of γ and β diversity depended on spatial variation in reflectance in the blue, red, and near infrared. Reflectance in the blue is linked to leaf chlorophyll content [15,30] and thus with leaf function as well as to shade in brightness normalized data. Reflectance in the red is linked to chlorophyll absorption. Reflectance and scattering in the near infrared is influenced by canopy structure and complexity [30] and water absorption in the 820 and 940–970 nm wavebands. Tuomisto et al. [20] and Dalmayne et al. [21] also found that community differences in β diversity correlated with differences in red and near infrared reflectance. Our PLSR results thus are consistent with the view that species diversity was correlated with spatial heterogeneity in canopy structure and function.

As estimated using PLSR models, restored grassland was 6–17% less diverse and exhibited greater spatial turnover in species composition and abundances when growing on a lowland clay than upland, silty clay soil. Diversity often varies inversely with productivity, but NDVI during spring did not differ between soil types in any year. Rather, it appears that soils differed in diversity partly because they differed in relative abundances of annual vs. perennial species. The vegetation of restored grassland was shaped by establishment and relative growth of two primary groups of species, the cohort of 38 perennial species that was planted and a cohort of approximately 25 annual grass and forb species that invaded following restoration. Annual species in this grassland often are relatively small-statured, cool season (C₃) plants that establish following rainfall in autumn and complete growth during spring when dominant warm-season C₄ perennial grasses are beginning growth. Dominant annuals included the forbs Gaillardia pulchella Foug and Monarda citriodora Cerv. ex Lag and grasses Bromus japonicus Thunb. ex Murray and Hordeum pusillum Nutt. Relative cover of annual species was greater on the silty clay than clay, implying that greater abundance of the often small-statured annuals increased diversity on the upland soil.

Extending diversity estimates to larger spatial scales than typically measured is a key motivation for developing remote sensing metrics of species diversity. Consequently, it is critical to understand the sensitivity of remote estimates to spatial scale. Diversity was successfully predicted using spatial variation in reflectance at each of the two spatial grains examined, but predictive equations differed between scales. A sensitivity to spatial scale also was evident in diversity estimated using the average CV in reflectance across wavebands [13]. Details in spectral heterogeneity relevant to species diversity may progressively be lost as the spatial scale of measurement is expanded. One consequence, as we observed, is that a given difference in spectral heterogeneity will predict a greater difference in diversity at large than smaller spatial scales. Spatial scale obviously must be considered to remotely estimate diversity, but we found that PLSR models of spectral heterogeneity predicted both γ and β diversity at spatial grains that differed by almost an order of magnitude in size. More generally, our analyses indicate that spectral heterogeneity relevant to estimating spatial differences in diversity exists at spatial scales of < 0.5 m² in the grasslands that we studied.

5. Conclusions

We demonstrate that both γ and β diversity of grassland can be statistically modeled by using spatial heterogeneity in canopy optical properties at small- to moderately-sized spatial grains. PLSR models using measurements of hyperspectral reflectance in visible to near infrared wavebands explained 59–85% of variance in γ diversity and 68–79% of variance in β diversity. Our analyses caution, however, that models are specific to the spatial grain at which they are developed.