Using Hidden Markov Models for Land Surface Phenology: An Evaluation Across a Range of Land Cover Types in Southeast Spain
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hidden Markov Models Basis
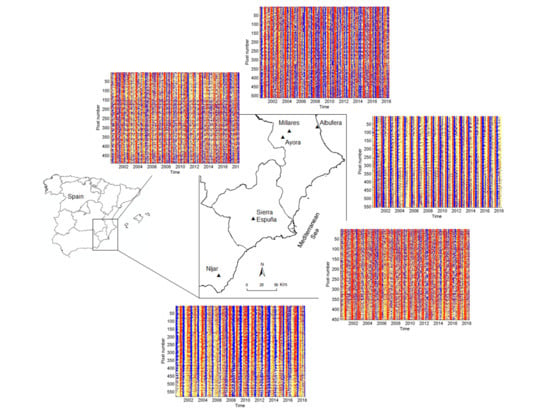
2.2. Study Areas
2.3. Data Adquisition
2.4. Methods of Analysis
2.4.1. Pixel Homogeneity Check
2.4.2. Hidden Markov Models Fitting and Analysis
2.4.3. Phenology Metrics Using Smoothing Methods
3. Results
3.1. Homogeneity Analysis and Seasonality Behavior in Different Land Cover Types
3.2. Estimated Hidden Markov Models Parameters and Inferred Hidden States
3.3. Comparison of Phenology Metrics Derived from Hidden Markov Models and Smoothing Methods
3.4. Performance of the Methods on Phenology Metrics Definition and Variability
3.5. Relation of Phenology Metrics with Climate Variables
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Reed, B.C.; Brown, J.F.; Vanderzee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring phenological variability from satellite imagery. J. Veg. Sci. 1994, 5, 703–714. [Google Scholar] [CrossRef]
- Helman, D. Land surface phenology: What do we really ‘see’ from space? Sci. Total Environ. 2018, 618, 665–673. [Google Scholar] [CrossRef] [PubMed]
- Morisette, J.T.; Richardson, A.D.; Knapp, A.K.; Fisher, J.I.; Graham, E.A.; Abatzoglou, J.; Wilson, B.E.; Breshears, D.D.; Henebry, G.M.; Hanes, J.M.; et al. Tracking the rhythm of the seasons in the face of global change: Phenological research in the 21st century. Front. Ecol. Environ. 2009, 7, 253–260. [Google Scholar] [CrossRef]
- Ivits, E.; Cherlet, M.; Tóth, G.; Sommer, S.; Mehl, W.; Vogt, J.; Micale, F. Combining satellite derived phenology with climate data for climate change impact assessment. Glob. Planet. Chang. 2012, 88–89, 85–97. [Google Scholar] [CrossRef]
- Garonna, I.; Jong, R.; Schaepman, M.E. Variability and evolution of global land surface phenology over the past three decades (1982–2012). Glo. Chang. Biol. 2016, 22, 1456–1468. [Google Scholar] [CrossRef] [PubMed]
- Moulin, S.; Kergoat, L.; Viovy, N.; Dedieu, G. Global-scale assessment of vegetation phenology using NOAA/AVHRR satellite measurements. J. Clim. 1997, 10, 1154–1170. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H. Climate controls on vegetation phenological patterns in northern mid—And high latitudes inferred from MODIS data. Glob. Chang. Biol. 2004, 10, 1133–1145. [Google Scholar] [CrossRef]
- Fisher, J.I.; Mustard, J.F. Cross-scalar satellite phenology from ground, Landsat, and MODIS data. Remote Sens. Environ. 2007, 109, 261–273. [Google Scholar] [CrossRef]
- Van Leeuwen, W.J.D.; Casady, G.; Neary, D.; Bautista, S.; Alloza, J.A.; Carmel, Y.; Wittenberg, L.; Malkinson, D.; Orr, B.J. Monitoring postwildfire vegetation response with remotely sensed time-series data in Spain, USA and Israel. Int. J. Wildland Fire 2010, 19, 75–93. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Dash, J.; Atkinson, P.M. Characterising the Land Surface Phenology of Europe Using Decadal MERIS Data. Remote Sens. 2015, 7, 9390–9409. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Yang, B.; Yang, Q.; Lu, L.; Wang, X.; Peng, Y. Temporal Trends and Spatial Variability of Vegetation Phenology over the Northern Hemisphere during 1982–2012. PLoS ONE 2016, 11, e0157134. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Chen, F.; Shi, L.; Niu, S. NDVI-derived forest area change and its driving factors in China. PLoS ONE 2018, 13, e0205885. [Google Scholar] [CrossRef] [PubMed]
- Workie, T.G.; Debella, H.J. Climate change and its effects on vegetation phenology across ecoregions of Ethiopia. Glob. Ecol. Conserv. 2018, 13, e00366. [Google Scholar] [CrossRef]
- Ganguly, S.; Friedl, M.A.; Tan, B.; Zhang, X.; Verma, M. Land surface phenology from MODIS: Characterization of the Collection 5 global land cover dynamics product. Remote Sens. Environ. 2010, 114, 1805–1816. [Google Scholar] [CrossRef]
- Didan, K. MOD13Q1 MODIS/Terra Vegetation Indices 16-Day L3 Global 250m SIN Grid V006. NASA EOSDIS Land Process. DAAC 2015. [Google Scholar] [CrossRef]
- Lu, L.; Kuenzer, C.; Wang, C.; Guo, H.; Li, Q. Evaluation of Three MODIS-Derived Vegetation Index Time Series for Dryland Vegetation Dynamics Monitoring. Remote Sens. 2015, 7, 7597–7614. [Google Scholar] [CrossRef] [Green Version]
- Testaa, S.; Soudanib, K.; Boschettic, L.; Borgogno Mondinoa, E. MODIS-derived EVI, NDVI and WDRVI time series to estimate phonological metrics in French deciduous forests. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 132–144. [Google Scholar] [CrossRef]
- Ferna, R.R.; Foxleya, E.A.; Brunob, A.; Morrisona, M.L. Suitability of NDVI and OSAVI as estimators of green biomass and coverage in a semi-arid rangeland. Ecol. Indic. 2018, 94, 16–21. [Google Scholar] [CrossRef]
- Moody, A.; Johnson, D. Land-surface phenologies from AVHRR using the discrete Fourier transform. Remote Sens. Environ. 2001, 75, 305–323. [Google Scholar] [CrossRef]
- Jakubauskas, M.E.; Legates, D.R.; Kastens, J.H. Harmonic analysis of time-series AVHRR NDVI data. Photogramm. Eng. Remote Sens. 2001, 67, 461–470. [Google Scholar]
- Jönsson, P.; Eklundh, L. Seasonality extraction and noise removal by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Wagenseil, H.; Samimi, C. Assessing spatio-temporal variations in plant phenology using Fourier analysis on ndvi time series: Results from a dry savannah environment in Namibia. Int. J. Remote Sens. 2006, 27, 3455–3471. [Google Scholar] [CrossRef]
- Bradley, B.A.; Jacob, R.W.; Hermance, J.F.; Mustard, J.F. A curve fitting procedure to derive inter-annual phenologies from time series of noisy satellite NDVI data. Remote Sens. Environ. 2007, 106, 137–145. [Google Scholar] [CrossRef]
- De Beurs, K.M.; Henebry, G.M. Spatio-temporal statistical methods for modeling land surface phenology. In Phenological Research: Methods for Environmental and Climate Change Analysis; Hudson, I.L., Keatley, M.R., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 177–208. [Google Scholar]
- Atkinson, P.M.; Jeganathan, C.; Dash, J.; Atzberger, C. Inter-comparison of four models for smoothing satellite sensor time-series data to estimate vegetation phenology. Remote Sens. Environ. 2012, 123, 400–417. [Google Scholar] [CrossRef]
- Cai, Z.; Jönsson, P.; Jin, H.; Eklundh, L. Performance of smoothing methods for reconstructing NDVI time-series and estimating vegetation phenology from MODIS data. Remote Sens. 2017, 9, 1271. [Google Scholar] [CrossRef]
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef] [Green Version]
- Gales, M.; Young, S. The application of hidden Markov models in speech recognition. Found. Trends Signal Process. 2008, 1, 195–304. [Google Scholar] [CrossRef]
- Bellone, E.; Hughes, J.P.; Guttorp, P. A hidden Markov model for downscaling synoptic atmospheric patterns to precipitation amounts. Clim. Res. 2000, 15, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Greene, A.M.; Robertson, A.W.; Smyth, P.; Triglia, S. Downscaling projections of Indian monsoon rainfall using a non-homogeneous hidden Markov model. Q. J. R. Meteorol. Soc. 2011, 137, 347–359. [Google Scholar] [CrossRef]
- Aas, K.; Eikvil, L.; Huseby, R.B. Applications of hidden Markov chains in image analysis. Pattern Recognit. 1999, 32, 703–713. [Google Scholar] [CrossRef] [Green Version]
- Visser, I.; Raijmakers, M.E.J.; Molenaar, P.C.M. Fitting hidden Markov models to psychological data. Sci. Program. 2002, 10, 185–199. [Google Scholar] [CrossRef]
- Molenaar, D.; Oberski, D.; Vermunt, J.; de Boeck, P. Hidden Markov item response theory models for responses and response times. Multivar. Behav. Res. 2016, 51, 606–626. [Google Scholar] [CrossRef] [PubMed]
- Macdonald, I.L.; Raubenheimer, D. Hidden Markov models and animal behavior. Biom. J. 1995, 37, 701–712. [Google Scholar] [CrossRef]
- Ver Hoef, J.M.; Cressie, N. Using hidden Markov chains and empirical Bayes change-point estimation for transect data. Environ. Ecol. Stat. 1997, 4, 247–264. [Google Scholar] [CrossRef]
- Rodríguez, F.; Bautista, S. Patch-gap analysis of presence-absence data in vegetation transects using hidden Markov models, with application to the characterisation of post-fire plant pattern disturbance in a semiarid pine forest. In Ecosystems and Sustainable Development III, Advances in Ecological Sciences 10; Brebbia, C.A., Villacampa, Y., Usó, J.L., Eds.; WIT Press: Southampton, UK, 2001; pp. 801–809. [Google Scholar]
- Franke, A.; Caelli, T.; Hudson, R.J. Analysis of movements and behavior of caribou (Rangifer tarandus) using hidden Markov models. Ecol. Model. 2004, 173, 259–270. [Google Scholar] [CrossRef]
- Tucker, B.C.; Anand, M. On the use of stationary versus hidden Markov models to detect simple versus complex ecological dynamics. Ecol. Model. 2005, 185, 177–193. [Google Scholar] [CrossRef]
- Franke, A.; Caelli, T.; Kuzyk, G.; Hudson, R.J. Prediction of wolf (Canis lupus) kill-sites using hidden Markov models. Ecol. Model. 2006, 197, 237–246. [Google Scholar] [CrossRef]
- Baldi, P.; Chauvin, Y.; Hunkapiller, T.; McClure, M.A. Hidden Markov models of biological primary sequence information. Proc. Natl. Acad. Sci. USA 1994, 91, 1059–1063. [Google Scholar] [CrossRef] [PubMed]
- Gollery, M. Handbook of Hidden Markov Models in Bioinformatics; Chapman and Hall/CRC: New York, NY, USA, 2008. [Google Scholar]
- Yoon, B.-J. Hidden Markov models and their applications in biological sequence analysis. Curr. Genom. 2009, 10, 402–415. [Google Scholar] [CrossRef] [PubMed]
- Westhead, D.R.; Vijayabaskar, M.S. (Eds.) Hidden Markov Models. Methods and Protocols; Humana Press/Springer: New York, NY, USA, 2017. [Google Scholar]
- Fjortoft, R.; Delignon, Y.; Pieczynski, W.; Sigelle, M.; Tupin, F. Unsupervised classification of radar images using hidden Markov chains and hidden Markov random fields. IEEE Trans. Geosci. Remote Sens. 2003, 41, 675–686. [Google Scholar] [CrossRef] [Green Version]
- Tso, B.; Olsen, R.C. Combining spectral and spatial information into hidden Markov models for unsupervised image classification. Int. J. Remote Sens. 2005, 26, 2113–2133. [Google Scholar] [CrossRef]
- Cerqueira Leite, P.B.; Queiroz Feitosa, R.; Roberto Formaggio, A.; da Costa, G.A.; Pakzad, K.; Del’Arco Sanches, I. Hidden Markov models for crop recognition in remote sensing image sequences. Pattern Recognit. Lett. 2011, 32, 19–26. [Google Scholar] [CrossRef]
- Ghamisi, P.; Benediktsson, J.A.; Ulfarsson, M.O. Spectral–spatial classification of hyperspectral images based on hidden Markov random fields. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2565–2574. [Google Scholar] [CrossRef]
- Siachalou, S.; Mallinis, G.; Tsakiri-Strati, M. A hidden Markov models approach for crop classification: Linking crop phenology to time series of multi-sensor remote sensing data. Remote Sens. 2015, 7, 3633–3650. [Google Scholar] [CrossRef]
- Yuan, Y.; Meng, Y.; Lin, L.; Sahli, H.; Yue, A.; Chen, J.; Zhao, Z.; Kong, Y.; He, D. Continuous change detection and classification using hidden Markov model: A case study for monitoring urban encroachment onto farmland in Beijing. Remote Sens. 2015, 7, 15318–15339. [Google Scholar] [CrossRef]
- Abercrombie, S.P.; Friedl, M.A. Improving the consistency of multitemporal land cover maps using a hidden Markov model. IEEE Trans. Geosci. Remote Sens. 2016, 54, 710–713. [Google Scholar] [CrossRef]
- Gong, W.; Fang, S.; Yang, G.; Ge, M. Using a hidden Markov model for improving the spatial-temporal consistency of time series land cover classification. ISPRS Int. J. Geo Inf. 2017, 6, 292. [Google Scholar] [CrossRef]
- Yuan, Y.; Lin, L.; Chen, J.; Sahli, H.; Chen, Y.; Wang, C.; Wu, B. A new framework for modelling and monitoring the conversion of cultivated land to built-up land based on a hierarchical hidden semi-Markov model using satellite image time series. Remote Sens. 2019, 11, 210. [Google Scholar] [CrossRef]
- Viovy, N.; Saint, G. Hidden Markov models applied to vegetation dynamics analysis using satellite remote sensing. IEEE Trans. Geosci. Remote Sens. 1994, 32, 906–917. [Google Scholar] [CrossRef]
- Shen, Y.; Wu, L.; Di, L.; Yu, G.; Tang, H.; Yu, G.; Shao, Y. Hidden Markov models for real-time estimation of corn progress stages using MODIS and meteorological data. Remote Sens. 2013, 5, 1734–1753. [Google Scholar] [CrossRef]
- García, M.A.; Moutahir, H.; Bautista, S.; Rodríguez, F. Determination of phenological parameters from MODIS derived NDVI data using hidden Markov models. In Proceedings of the SPIE Second International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2014), Paphos, Cyprus, 7–10 April 2014; Hadjimitsis, D.G., Themistocleous, K., Michaelides, S., Papadavid, G., Eds.; SPIE: Bellingham, WA, USA, 2014; Volume 9229, p. 92291K. [Google Scholar] [CrossRef]
- Cappé, O.; Moulines, E.; Rydén, T. Inference in Hidden Markov Models; Springer: New York, NY, USA, 2005. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Baum, L.E.; Petrie, T.; Soules, G.; Weiss, N. A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains. Ann. Math. Stat. 1970, 41, 164–171. [Google Scholar] [CrossRef]
- Viterbi, A.J. Error bounds for convolutional codes and an asymptotically optimal decoding algorithm. IEEE Trans. Inf. Theory 1967, 13, 260–269. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.R-project.org/ (accessed on 20 September 2018).
- Murphy, K. Hidden Markov Model (HMM) Toolbox for Matlab. Available online: https://www.cs.ubc.ca/~murphyk/Software/HMM/hmm.html (accessed on 12 June 2018).
- Forkel, M.; Carvalhais, N.; Verbesselt, J.; Mahecha, M.; Neigh, C.; Reichstein, M. Trend Change Detection in NDVI Time Series: Effects of Inter-Annual Variability and Methodology. Remote Sens. 2013, 5, 2113–2144. [Google Scholar] [CrossRef] [Green Version]
- Forkel, M.; Migliavacca, M.; Thonicke, K.; Reichstein, M.; Schaphoff, S.; Weber, U.; Carvalhais, N. Codominant water control on global interannual variability and trends in land surface phenology and greenness. Glob. Chang. Biol. 2015, 21, 3414–3435. [Google Scholar] [CrossRef] [PubMed]
- Forkel, M.; Wutzler, T. Greenbrown—Land Surface Phenology and Trend Analysis. A Package for the R Software. Version 2.2, 2015-04-15. Available online: http://greenbrown.r-forge.r-project.org/ (accessed on 10 May 2018).
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- White, M.A.; Thornton, P.E.; Running, W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Glob. Biogeochem. Cycles 1997, 11, 217–234. [Google Scholar] [CrossRef] [Green Version]
- Van Leeuwen, W.J.; Davison, J.E.; Casady, G.M.; Marsh, S.E. Phenological characterization of desert sky island vegetation communities with remotely sensed and climate time series data. Remote Sens. 2010, 2, 388–415. [Google Scholar] [CrossRef]
- Zhu, L.; Southworth, J. Disentangling the relationships between Net primary production and precipitation in Southern Africa savannas using satellite observations from 1982 to 2010. Remote Sens. 2013, 5, 3803–3825. [Google Scholar] [CrossRef]
- Yu, S.-Z. Hidden Semi-Markov Models: Theory, Algorithms and Applications; Elsevier: Amsterdam, The Netherlands, 2016; ISBN 978-0-12-802767-7. [Google Scholar]







| Site | Coordinates | Number of Pixels | Land Cover |
|---|---|---|---|
| Albufera | 39°15′N 0°18′W | 552 | Cropland |
| Millares | 39°12′N 0°51′W | 511 | Shrubland |
| Ayora | 39°06′N 0°58′W | 490 | Shrubland |
| Espuña | 37°51′N 1°32′W | 451 | Forest |
| Níjar | 36°59′N 2°11′W | 579 | Grass steppe |
| Transition Probabilities | Emissions | ||||||
|---|---|---|---|---|---|---|---|
| Site | S0− | S+ | S0+ | S− | Mean | SD | |
| Albufera | S0− | 0.923 | 0.077 | 0 | 0 | −22.5 | 54.2 |
| S+ | 0 | 0.868 | 0.132 | 0 | 449.0 | 263.9 | |
| S0+ | 0 | 0 | 0.845 | 0.154 | 64.6 | 86.1 | |
| S− | 0.090 | 0 | 0 | 0.910 | −317.9 | 170.9 | |
| Millares | S0− | 0.772 | 0.228 | 0 | 0 | −14.4 | 20.1 |
| S+ | 0 | 0.842 | 0.158 | 0 | 73.7 | 46.8 | |
| S0+ | 0 | 0 | 0.710 | 0.290 | 10.9 | 21.3 | |
| S− | 0.156 | 0 | 0 | 0.844 | −67.1 | 37.5 | |
| Ayora | S0− | 0.816 | 0.184 | 0 | 0 | −20.5 | 23.5 |
| S+ | 0 | 0.815 | 0.185 | 0 | 77.6 | 51.4 | |
| S0+ | 0 | 0 | 0.735 | 0.265 | 20.3 | 23.5 | |
| S− | 0.201 | 0 | 0 | 0.799 | −75.8 | 48.7 | |
| Espuña | S0− | 0.724 | 0.276 | 0 | 0 | 6.6 | 27.1 |
| S+ | 0 | 0.846 | 0.154 | 0 | 84.9 | 60.9 | |
| S0+ | 0 | 0 | 0.757 | 0.243 | −37.4 | 29.2 | |
| S− | 0.245 | 0 | 0 | 0.755 | −102.8 | 61.2 | |
| Níjar | S0− | 0.880 | 0.120 | 0 | 0 | −8.0 | 20.9 |
| S+ | 0 | 0.841 | 0.159 | 0 | 84.9 | 51.4 | |
| S0+ | 0 | 0 | 0.802 | 0.198 | 28.3 | 22.9 | |
| S− | 0.123 | 0 | 0 | 0.877 | −75.8 | 50.8 | |
| HMM | TS | gb_lin | gb_spl | gb_dbl | |
|---|---|---|---|---|---|
| HMM | 0.565 * | 0.791 ** | 0.556 * | 0.443 • | |
| TS | 0.194 | 0.505 * | 0.374 | 0.910 ** | |
| gb_lin | 0.587 * | 0.594 * | 0.836 ** | 0.498 * | |
| gb_spl | 0.436 • | 0.569 * | 0.663 ** | 0.243 | |
| gb_dbl | 0.352 | 0.779 ** | 0.770 ** | 0.681 ** |
| Millares | Ayora | Espuña | Níjar | |
|---|---|---|---|---|
| HMM – TS | 0.905 | 0.945 | 0.816 | 0.790 |
| HMM – gb_lin | 0.322 | 0.558 | 0.823 | 0.486 |
| TS – gb_lin | 0.282 | 0.630 | 0.648 | 0.265 |
| HMM – gb_spl | 0.342 | 0.493 | 0.809 | 0.618 |
| TS – gb_spl | 0.451 | 0.536 | 0.852 | 0.483 |
| HMM – gb_dbl | 0.878 | 0.854 | 0.778 | 0.528 |
| TS – gb_dbl | 0.942 | 0.873 | 0.866 | 0.406 |
| Albufera | Millares | Ayora | Espuña | Níjar | |
|---|---|---|---|---|---|
| HMM | 0 | 0 | 0 | 0 | 0 |
| TS | 0 | 0.5 | 0.9 | 0.6 | 0.1 |
| gb_lin | 3.6 | 6.6 | 7.6 | 9.8 | 15.3 |
| gb_spl | 4.6 | 12.7 | 13.5 | 5.6 | 10.0 |
| gb_dbl | 6.6 | 5.4 | 4.6 | 5.0 | 7.9 |
| Albufera | Millares | Ayora | Espuña | Níjar | |
|---|---|---|---|---|---|
| HMM | 6.0 | 4.8 | 7.6 | 5.2 | 9.4 |
| TS | 3.4 | 5.0 | 8.7 | 6.5 | 6.7 |
| gb_lin | 23.9 | 29.6 | 27.2 | 21.2 | 24.1 |
| gb_spl | 24.7 | 16.4 | 14.2 | 4.4 | 9.3 |
| gb_dbl | 12.3 | 6.8 | 9.0 | 8.1 | 7.5 |
| HMM | TS | gb_lin | gb_spl | db_dbl | |
|---|---|---|---|---|---|
| Precipitation | 0.512 ** | 0.488 ** | 0.070 | 0.156 | 0.175 |
| Temperature | 0.369 * | 0.213 • | 0.108 | 0.230 • | 0.201 • |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García, M.A.; Moutahir, H.; Casady, G.M.; Bautista, S.; Rodríguez, F. Using Hidden Markov Models for Land Surface Phenology: An Evaluation Across a Range of Land Cover Types in Southeast Spain. Remote Sens. 2019, 11, 507. https://doi.org/10.3390/rs11050507
García MA, Moutahir H, Casady GM, Bautista S, Rodríguez F. Using Hidden Markov Models for Land Surface Phenology: An Evaluation Across a Range of Land Cover Types in Southeast Spain. Remote Sensing. 2019; 11(5):507. https://doi.org/10.3390/rs11050507
Chicago/Turabian StyleGarcía, Miguel A., Hassane Moutahir, Grant M. Casady, Susana Bautista, and Francisco Rodríguez. 2019. "Using Hidden Markov Models for Land Surface Phenology: An Evaluation Across a Range of Land Cover Types in Southeast Spain" Remote Sensing 11, no. 5: 507. https://doi.org/10.3390/rs11050507
APA StyleGarcía, M. A., Moutahir, H., Casady, G. M., Bautista, S., & Rodríguez, F. (2019). Using Hidden Markov Models for Land Surface Phenology: An Evaluation Across a Range of Land Cover Types in Southeast Spain. Remote Sensing, 11(5), 507. https://doi.org/10.3390/rs11050507