Storm Event to Seasonal Evolution of Nearshore Bathymetry Derived from Shore-Based Video Imagery
Abstract
:1. Introduction
2. Methods
2.1. Study Site
2.2. Wave and Tidal Data
2.3. Wave Conditions and Storm Identification
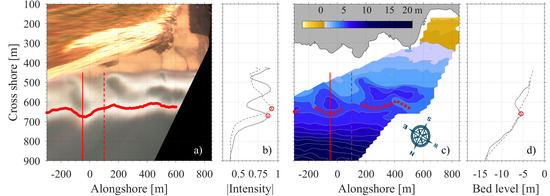
2.4. Video-Derived Bathymetries
2.5. Determination of the Bar Position
2.6. Cross-Shore Sediment Exchange
3. Results
3.1. Morphological Evolution
3.1.1. Extreme 2013–2014 Winter Season; Storm Erosion
3.1.2. Recovery, from Event to Seasonal Scale
3.1.3. Cross Shore Bar-Positions
3.1.4. Cross Shore Volumetric Change
4. Discussion
4.1. Multi-Scale Morphological Evolution: The Interplay Between an Event and Seasonal Scale
4.2. Pixel Intensities and Estimated Bathymetries
4.3. Challenges Related to Depth Inversion Under Extreme Conditions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Wave Statistics 2008–2017
| Period | [m] | [s] | [°] | [kW/m] | ΣP [MW/m] |
|---|---|---|---|---|---|
| 2008–2017 | 1.57 ± 0.94 | 10.51 ± 3.07 | 283.4 ± 26.7 | 17.48 ± 25.84 | 1360.2 |
| 2008 * | 1.94 ± 0.87 | 10.75 ±3.03 | 290.7 ±24.6 | 22.69 ±24.40 | 50.05 |
| 2009 | 1.62 ± 0.96 | 10.84 ± 2.89 | 281.9 ± 51.9 | 19.16 ± 27.15 | 159.86 |
| 2010 | 1.27 ± 0.69 | 10.05 ± 3.27 | 286.1 ± 27.5 | 10.16 ± 15.56 | 88.79 |
| 2011 | 1.66 ± 0.90 | 10.96 ± 3.02 | 281.4 ± 16.4 | 19.12 ± 24.28 | 166.87 |
| 2012 | 1.52 ± 0.86 | 9.98 ± 2.95 | 282.6 ± 21.7 | 14.89 ± 20.50 | 128.10 |
| 2013 | 1.55 ± 0.97 | 10.51 ± 3.09 | 283.0 ± 20.3 | 17.91 ± 27.77 | 153.15 |
| 2014 | 1.65 ± 1.12 | 10.70 ± 3.13 | 284.3 ± 20.2 | 20.10 ± 33.78 | 175.26 |
| 2015 | 1.70 ± 1.01 | 10.59 ± 3.10 | 283.9 ± 20.7 | 20.87 ± 27.83 | 180.64 |
| 2016 | 1.58 ± 0.96 | 10.69 ± 2.99 | 283.1 ± 20.8 | 18.31 ± 28.02 | 160.63 |
| 2017 * | 1.50 ± 0.86 | 10.15 ± 3.05 | 281.5 ± 19.6 | 14.95 ± 20.09 | 96.92 |
| Period | [m] | [s] | [°] | [kW/m] | ΣP [MW/m] |
|---|---|---|---|---|---|
| 2008–2017 winter | 1.90 ± 1.04 | 11.71 ± 3.00 | 285.3 ± 31.7 | 25.94 ± 32.19 | 1004.4 |
| 2008–2017 summer | 1.24 ± 0.68 | 9.33 ± 2.66 | 281.7 ± 20.7 | 9.10 ± 12.71 | 355.8 |
| 2008–2009 winter | 1.92 ± 0.93 | 11.61 ± 3.07 | 287.9 ± 24.5 | 24.97 ± 28.72 | 103.95 |
| 2009 summer | 1.30 ± 0.70 | 9.78 ± 2.33 | 281.4 ± 20.6 | 10.25 ± 12.35 | 42.88 |
| 2009–2010 winter | 1.68 ± 1.01 | 11.41 ± 3.28 | 284.5 ± 25.3 | 20.84 ± 28.89 | 90.95 |
| 2010 summer | 1.13 ± 0.50 | 9.21 ± 2.78 | 284.4 ± 23.2 | 6.78 ± 7.54 | 29.78 |
| 2010–2011 winter | 1.53 ± 0.91 | 11.49 ± 3.35 | 287.0 ± 27.4 | 18.36 ± 25.61 | 79.67 |
| 2011 summer | 1.43 ± 0.74 | 9.84 ± 2.69 | 279.8 ± 16.3 | 12.21 ± 15.55 | 53.49 |
| 2011–2012 winter | 1.93 ± 0.94 | 11.46 ± 2.87 | 283.4 ± 16.1 | 24.90 ± 28.12 | 105.92 |
| 2012 summer | 1.22 ± 0.70 | 8.79 ± 2.39 | 280.2 ± 22.4 | 8.45 ± 13.89 | 36.87 |
| 2012–2013 winter | 1.79 ± 0.96 | 11.42 ± 3.11 | 284.5 ± 23.2 | 21.97 ± 25.23 | 94.84 |
| 2013 summer | 1.23 ± 0.71 | 9.26 ± 2.62 | 281.3 ± 18.1 | 9.19 ± 13.93 | 38.93 |
| 2013–2014 winter | 2.30 ± 1.28 | 12.36 ± 2.82 | 287.0 ± 17.7 | 37.72 ± 47.02 | 163.17 |
| 2014 summer | 1.05 ± 0.60 | 9.15 ± 2.75 | 282.7 ± 22.5 | 6.42 ± 10.01 | 28.11 |
| 2014–2015 winter | 2.12 ± 1.03 | 11.87 ± 2.63 | 284.8 ± 18.7 | 30.74 ± 32.77 | 133.25 |
| 2015 summer | 1.26 ± 0.66 | 9.24 ± 2.78 | 283.0 ± 22.8 | 8.94 ± 11.45 | 39.20 |
| 2015–2016 winter | 2.16 ± 1.11 | 12.02 ± 2.76 | 283.3 ± 17.3 | 33.73 ± 37.58 | 145.54 |
| 2016 summer | 1.28 ± 0.68 | 9.42 ± 2.69 | 280.6 ± 19.1 | 9.75 ± 12.37 | 42.80 |
| 2016–2017 winter | 1.69 ± 0.92 | 11.72 ± 2.94 | 284.7 ± 24.5 | 20.25 ± 22.79 | 86.77 |
| 2017 summer | 1.29 ± 0.74 | 9.27 ± 2.65 | 280.6 ± 8.16 | 9.99 ± 14.42 | 43.75 |
Appendix B. cBathy Applications
| Period | Reference | Location | Frequency | #-obs | Type | Wave Cond. | Tide |
|---|---|---|---|---|---|---|---|
| 2009–2011 | Holman et al. [34] | Duck, NC USA | int. | 16 | Val. | calm/storm | micro |
| June 2013–March 2014 | Rutten et al. [36] | Sand Engine, The Netherlands | int. | 6 | Vol. | calm | micro |
| 13 July 2013 | Holman et al. [34] | Agate Beach, OR, USA | single | 1 | Val. | calm | meso |
| 17 May 2012 | Holman and Stanley [70] | New River Inlet, NC, USA | single | 1 | Val. | calm | micro |
| 10–17 April 2014 * | Bergsma et al. [35] | Porthtowan, Cornwall, UK | int. | 2 | Val. | calm | macro |
| 17–20 February 2013 | Wengrove et al. [71] | Kijkduin, The Netherlands | int. | 2 | Val. | calm | micro |
| 1–4 July 2013 | Radermacher et al. [72] | Sand Engine, The Netherlands | single | 1 | Val. | calm | micro |
| September 2015–September 2016 | Brodie et al. [37] | Duck, NC USA | full/int. | full/6 | Val./bar | calm/storm | micro |
| October 2013–February 2014 * | this study | Porthtowan, Cornwall, UK | full/int. | full/21 | BS, bar, Vol. | calm/storm | macro |
References
- Melet, A.; Meyssignac, B.; Almar, R.; Cozannet, G.L. Under-estimated wave contribution to coastal sea-level rise. Nat. Clim. Chang. 2018, 8, 234–239. [Google Scholar] [CrossRef]
- Dodet, G.; Bertin, X.; Taborda, R. Wave climate variability in the North-East Atlantic Ocean over the last six decades. Ocean Model. 2010, 31, 120–131. [Google Scholar] [CrossRef]
- Lazarus, E.D.; Ellis, M.A.; Murray, A.B.; Hall, D.M. An evolving research agenda for human-coastal systems. Geomorphology 2016, 256, 81–90. [Google Scholar] [CrossRef]
- Wang, X.L.; Feng, Y.; Swail, V.R. North Atlantic wave height trends as reconstructed from the 20th century reanalysis. Geophys. Res. Lett. 2012, 39, 1–6. [Google Scholar] [CrossRef]
- Woolf, D.; Wolf, J. Impacts of climate change on storms and waves. MCCIP Sci. Rev. 2013, 20–26. [Google Scholar] [CrossRef]
- Davidson, M.A.; Splinter, K.D.; Turner, I.L. A simple equilibrium model for predicting shoreline change. Coast. Eng. 2013, 73, 191–202. [Google Scholar] [CrossRef]
- Phillips, M.S.; Harley, M.D.; Turner, I.L.; Splinter, K.D.; Cox, R.J. Shoreline recovery on wave-dominated sandy coastlines: The role of sandbar morphodynamics and nearshore wave parameters. Mar. Geol. 2017, 385, 146–159. [Google Scholar] [CrossRef]
- Wright, L.; Short, A.D. Morphodynamic variability of surf zones and Beaches; A Synthesis. Mar. Geol. 1984, 56, 93–118. [Google Scholar] [CrossRef]
- Almar, R.; Marchesiello, P.; Almeida, L.P.; Thuan, D.H.; Tanaka, H.; Viet, N.T. Shoreline Response to a Sequence of Typhoon and Monsoon Events. Water 2017, 9, 364. [Google Scholar] [CrossRef]
- Martins, K.; Blenkinsopp, C.E.; Zang, J. Monitoring Individual Wave Characteristics in the Inner Surf with a 2-Dimensional Laser Scanner (LiDAR). J. Sens. 2016, 2016, 7965431. [Google Scholar] [CrossRef]
- Martins, K.; Blenkinsopp, C.E.; Power, H.E.; Bruder, B.; Puleo, J.A.; Bergsma, E.W.J. High-resolution monitoring of wave transformation in the surf zone using a LiDAR scanner array. Coast. Eng. 2017, 128, 37–43. [Google Scholar] [CrossRef]
- Larson, M.; Kraus, N.C. Temporal and spatial scales of beach profile change, Duck, North Carolina. Mar. Geol. 1994, 117, 75–94. [Google Scholar] [CrossRef]
- Birkemeier, W.A.; Baron, C.F.; Leffier, M.W.; Miller, H.C.; Strider, J.B.; Hathawa, K.K. SUPERDUCK Nearshore Processes Experiment: Data Summary, Miscellaneous Report; Technical Report; US Army Corps of Engineers: Washington, DC, USA, 1989.
- Sénéchal, N.; Gouriou, T.; Castelle, B.; Parisot, J.; Capo, S.; Bujan, S.; Howa, H. Morphodynamic response of a meso- to macro-tidal intermediate beach based on a long-term data set. Geomorphology 2009, 107, 263–274. [Google Scholar] [CrossRef] [Green Version]
- Harley, M.D.; Turner, I.L.; Short, A.D.; Ranasinghe, R. Assessment and integration of conventional, RTK-GPS and image-derived beach survey methods for daily to decadal coastal monitoring. Coast. Eng. 2011, 58, 194–205. [Google Scholar] [CrossRef]
- Poate, T.; Masselink, G.; Russell, P.; Austin, M. Morphodynamic variability of high-energy macrotidal beaches, Cornwall, UK. Mar. Geol. 2014, 350, 97–111. [Google Scholar] [CrossRef] [Green Version]
- Coco, G.; Sénechal, N.; Rejas, A.; Bryan, K.; Capo, S.; Parisot, J.; Brown, J.; MacMahan, J. Beach response to a sequence of extreme storms. Geomorphology 2014, 204, 493–501. [Google Scholar] [CrossRef] [Green Version]
- Masselink, G.; Scott, T.; Poate, T.; Russell, P.; Davidson, M.; Conley, D. The extreme 2013/2014 winter storms: Hydrodynamic forcing and coastal response along the southwest coast of England. Earth Surf. Process. Landf. 2015, 41, 378–391. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Callaghan, D.; Roelvink, D. Does a more sophisticated storm erosion model improve probabilistic erosion estimates? In Proceedings of the 7th International Conference on Coastal Dynamics, Arcachon, France, 24–28 June 2013. [Google Scholar]
- Bergsma, E.W.J.; Almar, R. Video-based depth inversion techniques, a method comparison with synthetic cases. Coast. Eng. 2018, 138, 199–209. [Google Scholar] [CrossRef]
- Wilson, G.; Özkan-Haller, H.; Holman, R. Data assimilation and bathymetric inversion in a two-dimensional horizontal surf zone model. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Wilson, G.; Özkan-Haller, H.; Holman, R.; Haller, M.; Honegger, D.; Chickadel, C. Surf zone bathymetry and circulation predictions via data assimilation of remote sensing observations. J. Geophys. Res. Oceans 2014. [Google Scholar] [CrossRef]
- Ludeno, G.; Reale, F.; Dentale, F.; Carratelli, E.P.; Natale, A.; Serafino, F. Estimating Nearshore Bathymetry from X-Band Radar Data. Coast. Ocean Obs. Syst. 2015, 265–280. [Google Scholar] [CrossRef]
- Plant, N.G.; Holman, R.A.; Freilich, M. A simple model for interannual sandbar behavior. J. Geophys. Res. 1999, 104, 15755–15776. [Google Scholar] [CrossRef] [Green Version]
- Van Enckevort, I.; Ruessink, B. Effect of Hydrodynamics and bathymetry on video estimates of nearshore sandbar position. J. Geophys. Res. 2001, 106, 16969–16979. [Google Scholar] [CrossRef]
- Plant, N.G.; Holland, K.T.; Holman, R.A. A dynamical attractor governs beach response to storms. Geophys. Res. Lett. 2006, 33, 1–6. [Google Scholar] [CrossRef]
- Price, T.; Ruessink, B. State Dynamics of a double sandbar system. Cont. Shelf Res. 2011, 31, 659–674. [Google Scholar] [CrossRef]
- Grilli, S.T. Depth inversion in shallow water based on nonlinear properties of shoaling periodic waves. Coast. Eng. 1998, 35, 185–209. [Google Scholar] [CrossRef] [Green Version]
- Bell, P.S. Shallow water bathymetry derived from an analysis of X-band marine radar images of waves. Coast. Eng. 1999, 37, 513–527. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A. Estimation of wave phase speed and nearshore bathymetry from video imagery. J. Geophys. Res. 2000, 105, 22015–22033. [Google Scholar] [CrossRef] [Green Version]
- Senet, C.M.; Seemann, J.; Flampouris, S.; Ziemer, F. Determination of Bathymetric and Current Maps by the Method DiSC Based on the Analysis of Nautical X-Band Radar Image Sequences of the Sea Surface (November 2007). IEEE Trans. Geosci. Remote Sens. 2008, 46, 2267–2279. [Google Scholar] [CrossRef]
- Almar, R.; Bonneton, P.; Senechal, N.; Roelvink, D. Wave Celerity From Video Imaging: A new method. In Proceedings of the 31st International Conference Coastal Engineering, Hamburg, Germany, 31 August–5 September 2008; pp. 1–14. [Google Scholar]
- Plant, N.G.; Holland, K.T.; Haller, M.C. Ocean Wavenumber Estimation From Wave-Resolving Time Series Imagery. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2644–2658. [Google Scholar] [CrossRef]
- Holman, R.A.; Plant, N.; Holland, T. cBathy: A Robust Algorithm For Estimating Nearshore Bathymetry. J. Geophys. Res. Oceans 2013, 118, 2595–2609. [Google Scholar] [CrossRef]
- Bergsma, E.W.J.; Conley, D.C.; Davidson, M.A.; O’Hare, T.J. Video-Based Nearshore Bathymetry Estimation in Macro-Tidal Environments. Mar. Geol. 2016, 374, 31–41. [Google Scholar] [CrossRef]
- Rutten, J.; de Jong, S.M.; Ruessink, G. Accuracy of Nearshore Bathymetry Inverted From X-Band Radar and Optical Video Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1106–1116. [Google Scholar] [CrossRef]
- Brodie, K.L.; Palmsten, M.L.; Hesser, T.J.; Dickhudt, P.J.; Raubenheimer, B.; Ladner, H.; Elgar, S. Evaluation of video-based linear depth inversion performance and applications using altimeters and hydrographic surveys in a wide range of environmental conditions. Coast. Eng. 2018, 136, 147–160. [Google Scholar] [CrossRef] [Green Version]
- Sembiring, L.; van Dongeren, A.; Winter, G.; van Ormondt, M.; Briere, C.; Roelvink, D. Nearshore bathymetry from video and the application to rip current predictions for the Dutch Coast. J. Coast. Res. 2014, 70, 354–359. [Google Scholar] [CrossRef]
- Bergsma, E.W.J. Application of an Improved Video Based Depth Inversion Technique to A Macrotidal Sandy Beach. Ph.D. Thesis, Plymouth University, CPRG, Plymouth, UK, 2017. [Google Scholar]
- Buscombe, D.; Scott, T. Coastal Geomorphology of North Cornwall: St Ives to Trevose Head. Internal Report for Wave Hub Impacts on Seabed and Shoreline Processes; Technical Report; University of Plymouth: Plymouth, UK, 2008. [Google Scholar]
- Scott, T.; Masselink, G.; Russell, P. Morphodynamic characteristics and classification of beaches in England and Wales. Mar. Geol. 2011, 286, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Holman, R.; Stanley, J. The history and technical capabilities of Argus. Coast. Eng. 2007, 54, 477–491. [Google Scholar] [CrossRef]
- Cahill, B.; Lewis, T. Wave period ratios and the calculation of wave power. In Proceedings of the 2nd Marine Energy Technology Symposium, Seattle, WA, USA, 15–17 April 2014; pp. 1–10. [Google Scholar]
- Leffler, K.E.; Jay, D.A. Enhancing tidal harmonic analysis: Robust (hybrid L1/L2) solutions. Cont. Shelf Res. 2009, 29, 78–88. [Google Scholar] [CrossRef]
- Morton, R.A.; Gibeaut, J.C.; Paine, J.G. Meso-scale transfer of sand during and after storms: Implications for prediction of shoreline movement. Mar. Geol. 1995, 126, 161–179. [Google Scholar] [CrossRef]
- Ferreira, O. Storm groups versus extreme single storms: Predicted erosion and management consequences. J. Coast. Res. 2005, 42, 221–227. [Google Scholar]
- Masselink, G.; Castelle, B.; Scott, T.; Dodet, G.; Suanez, S.; Jackson, D.; Floc’h, F. Extreme wave activity during 2013/2014 winter and morphological impacts along the Atlantic coast of Europe. Geophys. Res. Lett. 2016, 43, 2135–2143. [Google Scholar] [CrossRef] [Green Version]
- Harley, M.D.; Turner, I.L.; Short, A.D.; Ranasinghe, R. An empirical model of beach response to storms-SE Australia. In Proceedings of the 19th Australasian Conference on Coastal and Ocean Engineering, Wellington, New Zealand, 16–18 September 2009. [Google Scholar]
- Splinter, K.D.; Carley, J.T.; Golshani, A.; Tomlinson, R. A relationship to describe the cumulative impact of storm clusters on beach erosion. Coast. Eng. 2014, 83, 49–55. [Google Scholar] [CrossRef]
- Castelle, B.; Marieu, V.; Bujana, S.; Splinter, K.D.; Robinet, A.; Sénechal, N.; Ferreira, S. Impact of the winter 2013–2014 series of severe Western Europe storms on a double-barred sandy coast: Beach and dune erosion and megacusp embayments. Geomorphology 2015, 238, 135–148. [Google Scholar] [CrossRef]
- Merrifield, M.A.; Guza, R.T. Detecting Propagating Signals with Complex Empirical Orthogonal Functions: A Cautionary Note. J. Phys. Oceanogr. 1990, 20, 1628–1633. [Google Scholar] [CrossRef] [Green Version]
- Holland, T.K. Application of the Linear Dispersion Relation with Respect to Depth Inversion and Remotely Sensed Imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2060–2072. [Google Scholar] [CrossRef]
- McCarroll, R.J.; Masselink, G.; Valiente, N.G.; Scott, T.; King, E.V.; Conley, D.C. Wave and Tidal Controls on Embayment Circulation and Headland Bypassing for an Exposed, Macrotidal Site. J. Mar. Sci. Eng. 2018, 6, 94. [Google Scholar] [CrossRef]
- Almar, R.; Cienfuegos, R.; Catalán, P.A.; Birrien, F.; Castelle, B.; Michallet, H. Nearshore bathymetric inversion from video using a fully non-linear Boussinesq wave model. J. Coast. Res. 2011, 64, 20–24. [Google Scholar]
- Catálan, P.A.; Haller, M.C. Remote sensing of breaking wave phase speeds with application to non-linear depth inversions. Coast. Eng. 2008, 55, 93–111. [Google Scholar] [CrossRef]
- Lippmann, T.C.; Holman, R.A. Quantification of Sand Bar Morphology: A Video Technique Based on Wave Dissipation. J. Geophys. Res. 1989, 94, 995–1011. [Google Scholar] [CrossRef]
- Huntley, D.; Saulter, A.; Kingston, K.; Holman, R. Use Of Video Imagery To Test Model Predictions of Surf Heights. WIT Trans. Ecol. Environ. 2009, 126, 39–50. [Google Scholar]
- Kingston, K.S.; Ruessink, G.G.; van Enckevort, I.M.J.; Davidson, M.A. Artificial Neural Network Correction of Remotely Sensed Sandbar Location. Mar. Geol. 2000, 169, 137–160. [Google Scholar] [CrossRef]
- Loureiro, C.; Ferreira, O.; Cooper, J.A.G. Extreme erosion on high-energy embayed beaches: Influence of megarips and storm grouping. Geomorphology 2012, 139–140, 155–171. [Google Scholar] [CrossRef]
- Masselink, G.; Austin, M.; Scott, T.; Russell, P.E. Role of wave forcing, storms and NAO in outer bar dynamics on a high-energy, macro-tidal beach. Geomorphology 2014, 226, 76–93. [Google Scholar] [CrossRef] [Green Version]
- Castelle, B.; Scott, T.; Brander, R.W.; McCarroll, R. Rip current types, circulation and hazard. Earth-Sci. Rev. 2016, 163, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Wijnberg, K.; Holman, R. Video-observations of shoreward propagating accretionary waves. In Proceedings of the River Coastal and Estuarine Morphodynamics: RCEM 2007, Enschede, The Netherlands, 17–21 September 2007; Dohmen-Janssen, C.M., Hulscher, S.J.M.H., Eds.; pp. 737–743. [Google Scholar]
- Almar, R.; Castelle, B.; Ruessink, B.; Sénechal, N.; Bonneton, P.; Marieu, V. Two- and Three-dimensional double-sandbar system behaviour under intense wave forcing and a meso-macro tidal range. Cont. Shelf Res. 2010, 30, 781–792. [Google Scholar] [CrossRef]
- Ruessink, B.; Coco, G.; Ranasinghe, R.; Turner, I. Coupled and noncoupled behavior of three-dimensional morphological patterns in a double sandbar system. J. Geophys. Res. 2007, 112, C07002. [Google Scholar] [CrossRef]
- Dissanayake, P.; Brown, J.; Wisse, P.; Karunarathna, H. Comparison of storm cluster vs isolated event impacts on beach/dune morphodynamics. Estuar. Coast. Shelf Sci. 2015, 164, 301–312. [Google Scholar] [CrossRef] [Green Version]
- Dissanayake, P.; Brown, J.; Karunarathna, H. Impacts of storm chronology on the morphological changes of the Formby beach and dune system, UK. Nat. Hazards Earth Syst. Sci. 2015, 15, 1533–1543. [Google Scholar] [CrossRef] [Green Version]
- Van Enckevort, I.; Ruessink, B. Video observations of nearshore bar behaviour. Part 1: Alongshore uniform variability. Cont. Shelf Res. 2003, 23, 501–512. [Google Scholar] [CrossRef]
- Van Enckevort, I.; Ruessink, B. Video observations of nearshore bar behaviour. Part 2: Alongshore non-uniform variability. Cont. Shelf Res. 2003, 23, 513–532. [Google Scholar] [CrossRef]
- Stokes, C.; Davidson, M.; Russell, P. Observation and Prediction of Three-Dimensional Morphology at a High Energy Macrotidal Beach. Geomorphology 2015, 243, 1–13. [Google Scholar] [CrossRef]
- Holman, R.; Stanley, J. cBathy bathymetry estimation in the mixed wave-current domain of a tidal estuary. J. Coast. Res. 2013, 65, 1391–1396. [Google Scholar] [CrossRef]
- Wengrove, M.E.; Henriquez, M.; de Schipper, M.A.; Holman, R.; Stive, M. Monitoring morphology of the Sand Engine leeside using Argus. In Proceedings of the 7th International Conference on Coastal Dynamics, Arcachon, France, 24–28 June 2013. [Google Scholar]
- Radermacher, M.; Wengrove, M.; van Thiel de Vries, J.; Holman, R. Applicability of video-derived bathymetry estimates to nearshore current model predictions. J. Coast. Res. 2014, 70, 290–295. [Google Scholar] [CrossRef] [Green Version]











| Date | [m] | [m] | [sec] | [°] | TR [m] | [m] | Dur [hrs] | ΣP [MW/m] |
|---|---|---|---|---|---|---|---|---|
| 27 October 2013 | 5.6 | 4.5 | 16.8 | 2.3 | 1.5 | 19.0 | 3.14 | |
| 2 November 2013 | 7.1 | 5.4 | 13.9 | 5.8 | 3.2 | 17.5 | 2.35 | |
| 14 December 2013 | 4.3 | 4.1 | 15.5 | 4.1 | 2.4 | 17.0 | 0.72 | |
| 19 December 2013 | 4.8 | 4.5 | 15.2 | 4.9 | 2.9 | 4.5 | 0.69 | |
| 21 December 2013 | 5.0 | 4.1 | 16.4 | 4.5 | 2.7 | 25.0 | 2.83 | |
| 24 December 2013 | 5.3 | 4.5 | 15.6 | 3.8 | 2.4 | 20.5 | 3.07 | |
| 27 December 2013 | 6.8 | 5.2 | 15.7 | 3.2 | 2.0 | 16.5 | 3.12 | |
| 3 January 2014 | 5.9 | 4.9 | 16.6 | 6.6 | 3.7 | 26.0 | 4.66 | |
| 6 January 2014 | 5.8 | 4.9 | 18.6 | 5.4 | 3.1 | 27.5 | 5.70 | |
| 25 January 2014 | 6.5 | 4.5 | 14.6 | 3.3 | 2.0 | 58.0 | 6.42 | |
| 1 February 2014 | 7.3 | 5.2 | 17.1 | 7.0 | 4.0 | 27.5 | 5.20 | |
| 5 February 2014 * | 6.5 | 4.9 | 15.9 | 5.2 | 2.9 | 20.0 | 3.25 | |
| 10 December 2014 | 7.4 | 5.0 | 13.7 | 4.5 | 2.7 | 19.5 | 2.87 | |
| 14 January 2015 | 5.6 | 4.6 | 14.2 | 2.9 | 1.9 | 43.5 | 4.54 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bergsma, E.W.J.; Conley, D.C.; Davidson, M.A.; O'Hare, T.J.; Almar, R. Storm Event to Seasonal Evolution of Nearshore Bathymetry Derived from Shore-Based Video Imagery. Remote Sens. 2019, 11, 519. https://doi.org/10.3390/rs11050519
Bergsma EWJ, Conley DC, Davidson MA, O'Hare TJ, Almar R. Storm Event to Seasonal Evolution of Nearshore Bathymetry Derived from Shore-Based Video Imagery. Remote Sensing. 2019; 11(5):519. https://doi.org/10.3390/rs11050519
Chicago/Turabian StyleBergsma, Erwin W. J., Daniel C. Conley, Mark A. Davidson, Tim J. O'Hare, and Rafael Almar. 2019. "Storm Event to Seasonal Evolution of Nearshore Bathymetry Derived from Shore-Based Video Imagery" Remote Sensing 11, no. 5: 519. https://doi.org/10.3390/rs11050519
APA StyleBergsma, E. W. J., Conley, D. C., Davidson, M. A., O'Hare, T. J., & Almar, R. (2019). Storm Event to Seasonal Evolution of Nearshore Bathymetry Derived from Shore-Based Video Imagery. Remote Sensing, 11(5), 519. https://doi.org/10.3390/rs11050519