Evaluation of RadCalNet Output Data Using Landsat 7, Landsat 8, Sentinel 2A, and Sentinel 2B Sensors
Abstract
:1. Introduction
2. RadCalNet Site and Sensor Overview
2.1. RadCalNet Site Overview
2.1.1. Railroad Valley Playa
2.1.2. La Crau (LCFR)
2.1.3. Gobabeb (GONA)
2.2. Sensor Overview
3. Methodology
3.1. Data Selection
3.2. Cloud and Cloud Shadow Filtering
3.3. Image ROI Reflectance Extraction
3.4. Image View Angle Effect Corrections
3.5. RadCalNet Reflectance Extraction
3.6. Reflectance difference Analysis
3.7. TOA Reflectance Comparison Uncertaity Analysis
4. Results
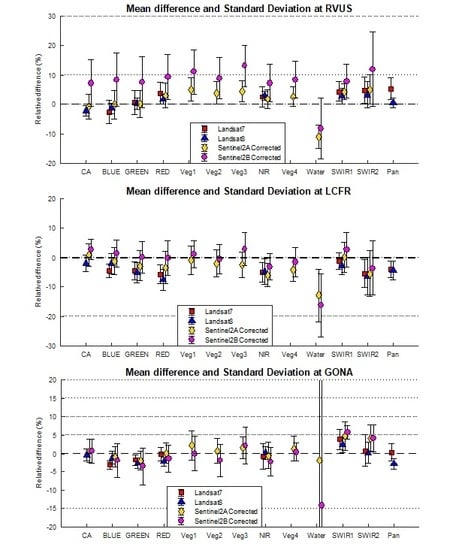
4.1. Comparison of RVUS Results
4.2. Comparison of LCFR Results
4.3. Comparison of GONA Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wenny, B.; Bouvet, M.; Thome, K.J.; Czapla-Myers, J.S.; Fox, N.; Gory, P.; Henry, P.; Meygret, A.; Li, C.; Ma, L.; et al. RadCalNet: A prototype radiometric calibration network for Earth observing imagers. In Proceedings of the Joint Agency Commercial Imagery Evaluation (JACIE) Workshop, Fort Worth, TX, USA, 12–14 April 2016. [Google Scholar]
- RadCalNet Technical Working Group. RadCalNet Guidance: Instrumentation and Data Processing (QA4EO-WGCV-RadCalNet-G3_v1); Committee on Earth Observation Satellites, 2018. Available online: https://www.radcalnet.org/documentation/RadCalNetGenDoc/G3-RadCalNetGuidance-InstrumentationAndDataProcessing_V1.pdf (accessed on 5 March 2019).
- Czapla-Myers, J.S.; Thome, K.J.; Leisso, N.P. Radiometric calibration of earth-observing sensors using an automated test site at Railroad Valley, Nevada. Can. J. Remote Sens. 2010, 36, 474–487. [Google Scholar] [CrossRef]
- University of Arizona. RadCalNet Site Description (QA4EO-WGCV-IVO-CSP-002_RVUS); Committee on Earth Observation Satellites: Railroad Valley, NV, USA, 2016. [Google Scholar]
- Czapla-Myers, J.; McCorkel, J.; Anderson, N.; Thome, K.; Biggar, S.; Helder, D.; Mishra, N. The ground-based absolute radiometric calibration of Landsat 8 OLI. Remote Sens. 2015, 7, 600–626. [Google Scholar] [CrossRef]
- CNES Physics for Optical Measurement Department. RadCalNet Site Description (QA4EO-WGCV-IVO-CSP-002_LCFR); Committee on Earth Observation Satellites: La Crau, France, 2016. [Google Scholar]
- National Physical Laboratory. RadCalNet Site Description (QA4EO-WGCV-IVO-CSP-002_GONA); Committee on Earth Observation Satellites: Gobabeb, Namibia, 2016. [Google Scholar]
- Zanter, K. Landsat 8 (L8) Data Users Handbook. Landsat Science Official Website. 2016. Available online: https://landsat.usgs.gov/landsat-8-l8-data-users-handbook (accessed on 20 January 2018).
- Gatti, A.; Bertolini, A. Sentinel-2 Products Specification Document. 2013. Available online: https://earth.esa.int/documents/247904/685211/Sentinel-2+Products+Specification+Document (accessed on 23 February 2015).
- Kaewmanee, M. Pseudo Invariant Calibration Sites: PICS Evolution. In Proceedings of the Conference on Characterization and Radiometric Calibration for Remote Sensing (CALCON), Logan, UT, USA, 18–20 June 2018. [Google Scholar]
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef] [Green Version]
- Mishra, N.; Haque, M.O.; Leigh, L.; Aaron, D.; Helder, D.; Markham, B. Radiometric cross calibration of Landsat 8 operational land imager (OLI) and Landsat 7 enhanced thematic mapper plus (ETM+). Remote Sens. 2014, 6, 12619–12638. [Google Scholar] [CrossRef]
- Czapla-Myers, J.; McCorkel, J.; Anderson, N.; Biggar, S. Earth-observing satellite intercomparison using the Radiometric Calibration Test Site at Railroad Valley. J. Appl. Remote Sens. 2017, 12, 012004. [Google Scholar] [CrossRef]
- Pinto, C.T.; Ponzoni, F.J.; Castro, R.M.; Leigh, L.; Kaewmanee, M.; Aaron, D.; Helder, D. Evaluation of the uncertainty in the spectral band adjustment factor (SBAF) for cross-calibration using Monte Carlo simulation. Remote Sens. Lett. 2016, 7, 837–846. [Google Scholar] [CrossRef]
- Chander, G.; Helder, D.L.; Aaron, D.; Mishra, N.; Shrestha, A.K. Assessment of spectral, misregistration, and spatial uncertainties inherent in the cross-calibration study. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1282–1296. [Google Scholar] [CrossRef]







































| Satellite and Sensor | ||||
|---|---|---|---|---|
| Landsat 7 ETM+ | Landsat 8 OLI | S2A MSI | S2B MSI | |
| Launch date | 1999-04-15 | 2013-02-11 | 2015-06-13 | 2017-03-07 |
| Spectral bands (used in this study) | 7 (7) | 9 (8) | 13 (11) | 13 (11) |
| Pixel size (m) | 30 | 30 | 10, 20, 60 | 10, 20, 60 |
| Conversion to TOA reflectance equation * | [8] | [9] | ||
| Diff% ± Standard Deviation% | ||||
|---|---|---|---|---|
| ETM+ | OLI | S2A MSI After Viewing Angle Effect Correction | S2B MSI After Viewing Angle Effect Correction | |
| # of Overpasses | 23 | 14 | 23 | 7 |
| CA | N/A | −2.2 ± 1.7 | −0.7 ± 4.4 | 7.3 ± 8.0 |
| Blue | −2.6 ± 3.9 | −1.4 ± 1.7 | −0.1 ± 4.9 | 8.4 ± 9.2 |
| Green | 0.7 ± 4.1 | 0.2 ± 1.9 | 0.2 ± 4.7 | 7.6 ± 8.8 |
| Red | 3.9 ± 3.9 | 1.8 ± 1.8 | 3.1 ± 4.3 | 9.4 ± 7.7 |
| Veg1 | N/A | N/A | 5.2 ± 4.1 | 11.2 ± 7.5 |
| Veg2 | N/A | N/A | 4.0 ± 3.9 | 8.9 ± 7.0 |
| Veg3 | N/A | N/A | 4.6 ± 3.7 | 13.3 ± 7.0 |
| NIR | 2.6 ± 3.6 | 3.0 ± 1.7 | 1.9 ± 3.3 | 7.3 ± 6.5 |
| Veg4 | N/A | N/A | 2.7 ± 3.3 | 8.4 ± 6.3 |
| Water | N/A | N/A | −11.0 ± 3.9 | −8.2 ± 10.3 |
| SWIR 1 | 4.4 ± 3.4 | 2.8 ± 2.8 | 4.4 ± 2.7 | 7.9 ± 5.8 |
| SWIR 2 | 4.9 ± 4.5 | 3.3 ± 4.5 | 5.2 ± 5.2 | 11.9 ± 12.7 |
| Pan | 5.4 ± 3.8 | 0.5 ± 1.6 | N/A | N/A |
| Diff% ± Standard Deviation% | ||||
|---|---|---|---|---|
| ETM+ | OLI | S2A MSI After Viewing Angle Effect Correction | S2B MSI After Viewing Angle Effect Correction | |
| # of Overpasses | 26 | 24 | 48 | 17 |
| CA | N/A | −1.8 ± 2.7 | 0.9 ± 3.8 | 2.8 ± 3.5 |
| Blue | −4.3 ± 2.3 | −1.9 ± 3.4 | −1.1 ± 4.6 | 1.5 ± 4.5 |
| Green | −4.4 ± 3.1 | −5.0 ± 3.6 | −2.8 ± 5.2 | 0.2 ± 5.3 |
| Red | −5.7 ± 3.3 | −7.5 ± 3.6 | −3.4 ± 5.6 | −0.1 ± 5.9 |
| Veg1 | N/A | N/A | −0.8 ± 4.9 | 1.2 ± 4.6 |
| Veg2 | N/A | N/A | −1.9 ± 4.6 | −0.4 ± 4.9 |
| Veg3 | N/A | N/A | −2.3 ± 4.3 | 3.0 ± 5.7 |
| NIR | −5.0 ± 3.4 | −4.7 ± 4.4 | −5.8 ± 4.2 | −3.0 ± 4.6 |
| Veg4 | N/A | N/A | −4.0 ± 4.2 | −1.4 ± 5.0 |
| Water | N/A | N/A | −12.8 ± 9.0 | −16.2 ± 10.8 |
| SWIR 1 | −1.1 ± 2.7 | −2.6 ± 2.9 | 0.2 ± 5.1 | 2.8 ± 5.8 |
| SWIR 2 | −5.3 ± 4.9 | −6.2 ± 6.4 | −5.5 ± 7.9 | −3.5 ± 9.2 |
| Pan | −3.9 ± 2.8 | −4.2 ± 3.2 | N/A | N/A |
| Diff% ± Standard Deviation% | ||||
|---|---|---|---|---|
| ETM+ | OLI | S2A MSI After Viewing Angle Effect Correction | S2B MSI After Viewing angle Effect Correction | |
| # of case | 14 | 14 | 20 | 6 |
| CA | N/A | −0.5 ± 1.7 | 0.7 ± 3.3 | 0.7 ± 3.3 |
| Blue | −3.1 ± 1.3 | −1.1 ± 1.8 | −0.9 ± 2.8 | −1.9 ± 4.6 |
| Green | −1.8 ± 1.4 | −2.7 ± 1.6 | −1.9 ± 2.6 | −3.5 ± 5.1 |
| Red | −0.2 ± 1.9 | −2.2 ± 1.4 | 0.1 ± 2.8 | −1.4 ± 3.7 |
| Veg1 | N/A | N/A | 2.3 ± 4.0 | −0.0 ± 4.8 |
| Veg2 | N/A | N/A | 0.7 ± 3.4 | −1.9 ± 4.5 |
| Veg3 | N/A | N/A | 1.7 ± 2.9 | 2.2 ± 5.1 |
| NIR | −0.8 ± 3.5 | 0.2 ± 1.7 | −0.6 ± 3.6 | −2.3 ± 4.0 |
| Veg4 | N/A | N/A | 1.3 ± 3.4 | 0.4 ± 2.5 |
| Water | N/A | N/A | −1.9 ± 55.1 | −14.2 ± 35.5 |
| SWIR 1 | 3.9 ± 2.7 | 2.5 ± 2.1 | 4.8 ± 3.8 | 5.8 ± 1.9 |
| SWIR 2 | 0.8 ± 4.3 | 0.2 ± 2.9 | 4.2 ± 3.5 | 4.1 ± 3.7 |
| Pan | 0.3 ± 2.4 | −2.9 ± 1.5 | N/A | N/A |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, X.; Leigh, L.; Teixeira Pinto, C.; Helder, D. Evaluation of RadCalNet Output Data Using Landsat 7, Landsat 8, Sentinel 2A, and Sentinel 2B Sensors. Remote Sens. 2019, 11, 541. https://doi.org/10.3390/rs11050541
Jing X, Leigh L, Teixeira Pinto C, Helder D. Evaluation of RadCalNet Output Data Using Landsat 7, Landsat 8, Sentinel 2A, and Sentinel 2B Sensors. Remote Sensing. 2019; 11(5):541. https://doi.org/10.3390/rs11050541
Chicago/Turabian StyleJing, Xin, Larry Leigh, Cibele Teixeira Pinto, and Dennis Helder. 2019. "Evaluation of RadCalNet Output Data Using Landsat 7, Landsat 8, Sentinel 2A, and Sentinel 2B Sensors" Remote Sensing 11, no. 5: 541. https://doi.org/10.3390/rs11050541
APA StyleJing, X., Leigh, L., Teixeira Pinto, C., & Helder, D. (2019). Evaluation of RadCalNet Output Data Using Landsat 7, Landsat 8, Sentinel 2A, and Sentinel 2B Sensors. Remote Sensing, 11(5), 541. https://doi.org/10.3390/rs11050541