Objective Estimation of Tropical Cyclone Intensity from Active and Passive Microwave Remote Sensing Observations in the Northwestern Pacific Ocean
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data Description
2.2.1. HY-2A Microwave Scatterometer
2.2.2. SSMIS Microwave Radiometer
2.2.3. Best-Track Data
3. Methodology
3.1. Relationship between the Satellite-Observed Parameters and the Maximum Wind Speed
3.1.1. TB Parameters
3.1.2. SSW Parameters
3.2. Estimation of the Maximum Wind Speed using Selected Parameters
4. Experimental Results
4.1. Model Verification
4.1.1. Comparison with the TC Best-Track Wind Speed Estimates
4.1.2. Comparison with the Passive-Only Model
4.1.3. Comparison with Other Existing Models
4.1.4. The Impact of Overpass Time Difference on Model Estimation
4.2. Case Studies
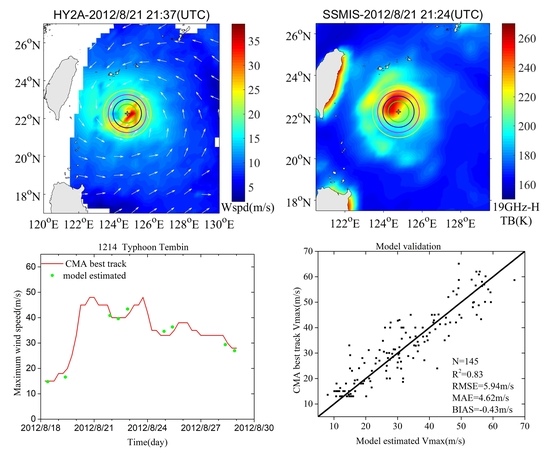
4.2.1. Typhoon Tembin (1214)
4.2.2. Typhoon Noru (1705)
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tang, D.L.; Sui, G.; Lavy, G.; Pozdnyakov, D.; Song, Y.T.; Switzer, A.D. Typhoon Impact and Crisis Management; Springer: Berlin, Germany, 2014. [Google Scholar]
- Dvorak, V.F. Tropical cyclone intensity analysis and forecasting from satellite imagery. Mon. Weather Rev. 1975, 103, 420–430. [Google Scholar] [CrossRef]
- Dvorak, V.F. Tropical Cyclone Intensity Analysis Using Satellite Data; National Environmental Satellite, Data, and Information Service, National Oceanic and Atmospheric Administration, US Department of Commerce: Silver Spring, MD, USA, 1984; Volume 11.
- Velden, C.S.; Olander, T.L.; Zehr, R.M. Development of an objective scheme to estimate tropical cyclone intensity from digital geostationary satellite infrared imagery. Weather Forecast. 1998, 13, 172–186. [Google Scholar] [CrossRef]
- Olander, T.L.; Velden, C.S.; Turk, M.A. Development of the Advanced Objective Dvorak Technique (AODT)–Current progress and future directions. In Proceedings of the 25th Conference on Hurricanes and Tropical Meteorology, San Diego, CA, USA, 29 April–3 May 2002; pp. 585–586. [Google Scholar]
- Olander, T.L.; Velden, C.S. The advanced Dvorak technique: Continued development of an objective scheme to estimate tropical cyclone intensity using geostationary infrared satellite imagery. Weather Forecast. 2007, 22, 287–298. [Google Scholar] [CrossRef]
- Piñeros, M.F.; Ritchie, E.A.; Tyo, J.S. Objective measures of tropical cyclone structure and intensity change from remotely sensed infrared image data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3574–3580. [Google Scholar] [CrossRef]
- Piñeros, M.F.; Ritchie, E.A.; Tyo, J.S. Estimating tropical cyclone intensity from infrared image data. Weather Forecast. 2011, 26, 690–698. [Google Scholar] [CrossRef]
- Ritchie, E.A.; Valliere-Kelley, G.; Piñeros, M.F.; Tyo, J.S. Tropical cyclone intensity estimation in the North Atlantic Basin using an improved deviation angle variance technique. Weather Forecast. 2012, 27, 1264–1277. [Google Scholar] [CrossRef]
- Ritchie, E.A.; Wood, K.M.; Rodríguez-Herrera, O.G.; Piñeros, M.F.; Tyo, J.S. Satellite-derived tropical cyclone intensity in the north pacific ocean using the deviation-angle variance technique. Weather Forecast. 2014, 29, 505–516. [Google Scholar] [CrossRef]
- Zhang, C.-J.; Qian, J.-F.; Ma, L.-M.; Lu, X.-Q. Tropical Cyclone Intensity Estimation Using RVM and DADI Based on Infrared Brightness Temperature. Weather Forecast. 2016, 31, 1643–1654. [Google Scholar] [CrossRef]
- Lu, X.; Yu, H.; Yang, X.; Li, X. Estimating Tropical Cyclone Size in the Northwestern Pacific from Geostationary Satellite Infrared Images. Remote Sens. 2017, 9, 728. [Google Scholar] [CrossRef]
- Hawkins, J.D.; Lee, T.; Turk, F.; Richardson, K.; Sampson, C.; Kent, J. Mapping tropical cyclone characteristics via passive microwave remote sensing. In Proceedings of the 11th Conference on Satellite Meteorology and Oceanography, Madison, WI, USA, 15–18 October 2001. [Google Scholar]
- Wimmers, A.J.; Velden, C.S. Objectively determining the rotational center of tropical cyclones in passive microwave satellite imagery. J. Appl. Meteorol. Climatol. 2010, 49, 2013–2034. [Google Scholar] [CrossRef]
- Bankert, R.L.; Tag, P.M. An automated method to estimate tropical cyclone intensity using SSM/I imagery. J. Appl. Meteorol. 2002, 41, 461–472. [Google Scholar] [CrossRef]
- Bankert, R.L.; Cossuth, J. Tropical Cyclone Intensity Estimation via Passive Microwave Data Features. In Proceedings of the 32rd Conf. on Hurricanes and Tropical Meteorology, San Juan, Puerto Rico, 17–22 April 2016. [Google Scholar]
- Hoshino, S.; Nakazawa, T. Estimation of tropical cyclone’s intensity using TRMM/TMI brightness temperature data. J. Meteorol. Soc. Jpn. 2007, 85, 437–454. [Google Scholar] [CrossRef]
- Yang, S.; Hawkins, J.; Richardson, K. The improved NRL tropical cyclone monitoring system with a unified microwave brightness temperature calibration scheme. Remote Sens. 2014, 6, 4563–4581. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, X.; Li, Z.; Yu, Y.; Bi, H.; Ma, S.; Li, X. Estimation of tropical cyclone parameters and wind fields from SAR images. Sci. China Earth Sci. 2013, 56, 1977–1987. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.; Perrie, W.; Hwang, P.A.; Zhang, B.; Yang, X. A Hurricane Wind Speed Retrieval Model for C-Band RADARSAT-2 Cross-Polarization ScanSAR Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4766–4774. [Google Scholar] [CrossRef]
- Jiang, H.; Tao, C.; Pei, Y. Estimation of Tropical Cyclone Intensity in the North Atlantic and North Eastern Pacific Basins Using TRMM Satellite Passive Microwave Observations. J. Appl. Meteorol. Climatol. 2019, 58, 185–197. [Google Scholar] [CrossRef]
- Said, F.; Long, D.G. Determining selected tropical cyclone characteristics using QuikSCAT’s ultra-high resolution images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 857–869. [Google Scholar] [CrossRef]
- Liu, S.; Li, Z.; Yang, X.; Pichel, G.W.; Yu, Y.; Zheng, Q.; Li, X. Atmospheric frontal gravity waves observed in satellite SAR images of the Bohai Sea and Huanghai Sea. Acta Oceanol. Sin. 2010, 29, 35–43. [Google Scholar] [CrossRef]
- Shao, W.; Li, X.; Hwang, P.; Zhang, B.; Yang, X. Bridging the gap between cyclone wind and wave by C-band SAR measurements. J. Geophys. Res. Ocean. 2017, 122. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Zheng, Q.; Gu, X.; Pichel, W.G.; Li, Z. Comparison of Ocean-Surface Winds Retrieved from QuikSCAT Scatterometer and Radarsat-1 SAR in Offshore Waters of the U.S. West Coast. IEEE Geosci. Remote Sens. Lett. 2011, 8, 163–167. [Google Scholar] [CrossRef]
- Chen, L.; Ding, Y. An Introduction to Typhoons in the Western Pacific Ocean; Science Press: Beijing, China, 1979. [Google Scholar]
- Stiles, B.W.; Dunbar, R.S. A neural network technique for improving the accuracy of scatterometer winds in rainy conditions. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3114–3122. [Google Scholar] [CrossRef]
- Stiles, B.W.; Danielson, R.E.; Poulsen, W.L.; Brennan, M.J.; Hristova-Veleva, S.; Shen, T.-P.; Fore, A.G. Optimized tropical cyclone winds from QuikSCAT: A neural network approach. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7418–7434. [Google Scholar] [CrossRef]
- Lin, M.; Zhang, Y.; Song, Q.; Xie, X.; Zou, J. Application of HY-2 Satellite Microwave Scattering Meter in Typhoon Monitoring in Northwest Pacific Ocean. Chin. Eng. Sci. 2014, 16, 46–53. [Google Scholar]
- Yang, X.; Liu, G.; Li, Z.; Yu, Y. Preliminary validation of ocean surface vector winds estimated from China’s HY-2A scatterometer. Int. J. Remote Sens. 2014, 35, 4532–4543. [Google Scholar] [CrossRef]
- Yan, B.; Weng, F. Intercalibration between special sensor microwave imager/sounder and special sensor microwave imager. IEEE Trans. Geosci. Remote Sens. 2008, 46, 984–995. [Google Scholar]
- Kerola, D.X. Calibration of Special Sensor Microwave Imager/Sounder (SSMIS) upper air brightness temperature measurements using a comprehensive radiative transfer model. Radio Sci. 2006, 41, 1–11. [Google Scholar] [CrossRef]
- Velden, C.; Harper, B.; Wells, F.; Beven, J.L.; Zehr, R.; Olander, T.; Mayfield, M.; Guard, C.C.; Lander, M.; Edson, R. The Dvorak tropical cyclone intensity estimation technique: A satellite-based method that has endured for over 30 years. Bull. Am. Meteorol. Soc. 2006, 87, 1195–1210. [Google Scholar] [CrossRef]
- Gray, W.M.; Neumann, C.; Tsui, T.L. Assessment of the role of aircraft reconnaissance on tropical cyclone analysis and forecasting. Bull. Am. Meteorol. Soc. 1991, 72, 1867–1884. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An overview of the China Meteorological Administration tropical cyclone database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Cecil, D.J.; Zipser, E.J. Relationships between tropical cyclone intensity and satellite-based indicators of inner core convection: 85-GHz ice-scattering signature and lightning. Mon. Weather Rev. 1999, 127, 103–123. [Google Scholar] [CrossRef]
- Lee, T.F.; Turk, F.J.; Hawkins, J.; Richardson, K. Interpretation of TRMM TMI Images of Tropical Cyclones. Earth Interact. 2002, 6, 1. [Google Scholar] [CrossRef]
- Weng, F.; Grody, N.C. Retrieval of cloud liquid water using the Special Sensor Microwave Imager. J. Geophys. Res. Atmos. 1994, 99, 25535–25551. [Google Scholar] [CrossRef]
- Yoshida, S.; Sakai, M.; Shouji, A. Estimation of tropical cyclone’s intensity using Aqua/AMSR-E data. Meteorol. Satell. Cent. Tech. Note 2009, 13–42. [Google Scholar]
- Olander, T.L.; Velden, C.S. Tropical cyclone convection and intensity analysis using differenced infrared and water vapor imagery. Weather Forecast. 2009, 24, 1558–1572. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, C.; Sun, R.; Wang, Z. A Multiple Linear Regression Model for Tropical Cyclone Intensity Estimation from Satellite Infrared Images. Atmosphere 2016, 7, 40. [Google Scholar] [CrossRef]
- Spencer, R.W.; Hood, R.E.; Goodman, H.M. Precipitation Retrieval over Land and Ocean with the SSM/I: Identification and Characteristics of the Scattering Signal. J. Atmos. Ocean. Technol. 1989, 6, 254–273. [Google Scholar] [CrossRef] [Green Version]
- Demuth, J.L.; DeMaria, M.; Knaff, J.A.; Vonder Haar, T.H. Evaluation of Advanced Microwave Sounding Unit tropical-cyclone intensity and size estimation algorithms. J. Appl. Meteorol. 2004, 43, 282–296. [Google Scholar] [CrossRef]
- Demuth, J.L.; DeMaria, M.; Knaff, J.A. Improvement of Advanced Microwave Sounding Unit tropical cyclone intensity and size estimation algorithms. J. Appl. Meteorol. Climatol. 2006, 45, 1573–1581. [Google Scholar] [CrossRef]
- Kossin, J.P.; Knapp, K.R.; Vimont, D.J.; Murnane, R.J.; Harper, B.A. A globally consistent reanalysis of hurricane variability and trends. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
- Knaff, J.A.; Brown, D.P.; Courtney, J.; Gallina, G.M.; Beven, J.L. An evaluation of Dvorak technique–based tropical cyclone intensity estimates. Weather Forecast. 2010, 25, 1362–1379. [Google Scholar] [CrossRef]
- Fetanat, G.; Homaifar, A.; Knapp, K.R. Objective tropical cyclone intensity estimation using analogs of spatial features in satellite data. Weather Forecast. 2013, 28, 1446–1459. [Google Scholar] [CrossRef]
- Pradhan, R.; Aygun, R.S.; Maskey, M.; Ramachandran, R.; Cecil, D.J. Tropical Cyclone Intensity Estimation Using a Deep Convolutional Neural Network. IEEE Trans. Image Process. 2018, 27, 692–702. [Google Scholar] [CrossRef] [PubMed]
- Wimmers, A.J.; Velden, C.S. Advancements in objective multisatellite tropical cyclone center fixing. J. Appl. Meteorol. Climatol. 2016, 55, 197–212. [Google Scholar] [CrossRef]
- Sapp, J.W.; Alsweiss, S.O.; Jelenak, Z.; Chang, P.S.; Carswell, J. Stepped Frequency Microwave Radiometer Wind-Speed Retrieval Improvements. Remote Sens. 2019, 11, 214. [Google Scholar] [CrossRef]












| Year | Training Data | Test Data | ||
|---|---|---|---|---|
| TCs | Sample | TCs | Sample | |
| 2012 | 18 | 55 | 5 | 31 |
| 2013 | 23 | 63 | 5 | 29 |
| 2014 | 15 | 43 | 3 | 10 |
| 2015 | 16 | 47 | 7 | 57 |
| 2016 | 9 | 15 | 1 | 4 |
| 2017 | 15 | 38 | 2 | 14 |
| Total | 96 | 261 | 23 | 145 |
| TB Parameter | Correlation Coefficient | Root Mean Square Error (m/s) |
|---|---|---|
| TB19H_MIN_C100 | 0.84 | 6.67 |
| TB37H_MIN_C125 | 0.84 | 6.72 |
| TB19H_MIN_C125 | 0.83 | 6.98 |
| TB37H_MIN_C100 | 0.83 | 7.00 |
| TB19H_MIN_C075 | 0.82 | 7.01 |
| TB22V_RAPT270_C100 | 0.82 | 7.04 |
| TB22V_RAPT270_C125 | 0.82 | 7.14 |
| TB19H_MIN_A075100 | 0.82 | 7.17 |
| TB22V_RAPT270_C075 | 0.82 | 7.19 |
| TB19V_MIN_C100 | 0.81 | 7.19 |
| SSW Parameter | Correlation Coefficient | RMSE(m/s) |
|---|---|---|
| SSW_MEAN_C100 | 0.83 | 7.09 |
| SSW_MEAN_C125 | 0.82 | 7.10 |
| SSW_MEAN_C150 | 0.81 | 7.20 |
| SSW_MIN_C100 | 0.81 | 7.29 |
| SSW_MEAN_C075 | 0.81 | 7.24 |
| SSW_MEAN_C175 | 0.81 | 7.38 |
| SSW_MIN_A075100 | 0.80 | 7.20 |
| SSW_MEAN_C200 | 0.79 | 7.57 |
| SSW_MEAN_A075100 | 0.79 | 7.36 |
| SSW_MEAN_C225 | 0.78 | 7.78 |
| SSW_MEAN_A100125 | 0.78 | 7.69 |
| SSW_MIN_C075 | 0.78 | 7.70 |
| SSW_MIN_C125 | 0.78 | 7.87 |
| SSW_MAX_C100 | 0.77 | 7.90 |
| SSW_MAX_C125 | 0.77 | 7.91 |
| Equation | a | Pi | b | Pj | c | Pk | d | R2 | RMSE |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.24 | TBH19_RAPT250_C125 | 0.35 | TBH37_MIN_C100 | 0.070 | TBV22_RAPT270_C125 | −50.16 | 0.79 | 6.51 |
| 2 | 1.40 | TBH19_MIN_C100 | 0.23 | TBH19_RAPT250_C125 | −1.78 | TBV19_MIN_C100 | 167.71 | 0.79 | 6.55 |
| 3 | 0.39 | TB19H_MIN_C100 | 0.21 | TBH19_RAPT250_C125 | 0.059 | TBV22_RAPT270_C125 | −51.12 | 0.79 | 6.55 |
| 4 | 0.44 | TBH19_MIN_C100 | 0.22 | TBH19_RAPT250_C125 | −0.07 | TBPCT91_RAPT230_C075 | −52.95 | 0.79 | 6.55 |
| 5 | 0.33 | TBH19_MIN_C100 | −0.15 | TBPCT91_RAPT230_C075 | 0.15 | TBV22_RAPT270_C125 | −27.28 | 0.79 | 6.55 |
| 6 | 0.13 | TBH19_MIN_C100 | 0.27 | TBH19_RAPT250_C125 | 0.30 | TBH37_MIN_C100 | −64.20 | 0.79 | 6.56 |
| 7 | 0.43 | TBH19_MIN_C100 | 0.24 | TBH19_RAPT250_C125 | 0.36 | TBV22_MAX_C150 | −154.64 | 0.79 | 6.59 |
| 8 | 0.28 | TBH19_RAPT250_C125 | 0.38 | TBH37_MIN_C100 | 0.47 | TBV22_MAX_C150 | −182.53 | 0.79 | 6.60 |
| 9 | 1.41 | TBH19_MIN_C100 | −1.87 | TBV19_MIN_C100 | 0.13 | TBV22_RAPT270_C125 | 184.14 | 0.79 | 6.60 |
| 10 | −0.16 | TBPCT91_RAPT230_C075 | 0.29 | TBH37_MIN_C100 | 0.17 | TBV22_RAPT270_C125 | −24.55 | 0.79 | 6.61 |
| Technique | Sensors | Verification Against | RMSE (m/s) | Mean Absolute Error (m/s) | References |
|---|---|---|---|---|---|
| Feature-based K-nearest | SSM/I | Best Track | 9.31–10.19 | 7.20–8.23 | Bankert and Tag [15] |
| Warm Core Anomaly | AMSU | Best Track | 7.20 | 5.40 | Demuth et al. [43,44] |
| Multivariate Regression | IR | Within 3 hr aircraft reconnaissance-based best track | 8.59 | 6.79 | Kossin et al. [45] |
| Advanced Dvorak Technique | IR | Within 1 hr aircraft reconnaissance-based best track | 7.67 | 5.61 | Olander and Velden [6] |
| Dvorak Technique (DT) | Visible/IR | Within 2 hr aircraft reconnaissance-based best track | 3.09–7.20 (avg. ~5.14) | 2.57–5.66 (avg. ~4.12) | Knaff et al. [46] |
| Deviation Angle Variance (DAV) | IR | Best Track | 6.17–7.72 | - | Ritchie et al. [9,10] |
| Feature Analogs in Satellite Imagery (FASI) | IR | Within 12 hr aircraft reconnaissance-based best track | 6.53 | 5.61 | Fetanat et al. [47] |
| Deep Convolutional Neutral Network | IR | Aircraft reconnaissance dataset | 4.63–8.23 (avg. ~6.02) | - | Pradhan et al. [48] |
| PMW-IE Combined Model for t = 6 hr | TMI | Best Track/Within 3 hr aircraft reconnaissance-based best track | 6.17/6.48 | 4.63/4.94 | Jiang et al. [21] |
| The proposed model | SSMIS/HY-2A | Best Track | 5.94 | 4.62 | This study |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, K.; Yang, X.; Zhang, M.; Li, Z.; Kong, F. Objective Estimation of Tropical Cyclone Intensity from Active and Passive Microwave Remote Sensing Observations in the Northwestern Pacific Ocean. Remote Sens. 2019, 11, 627. https://doi.org/10.3390/rs11060627
Xiang K, Yang X, Zhang M, Li Z, Kong F. Objective Estimation of Tropical Cyclone Intensity from Active and Passive Microwave Remote Sensing Observations in the Northwestern Pacific Ocean. Remote Sensing. 2019; 11(6):627. https://doi.org/10.3390/rs11060627
Chicago/Turabian StyleXiang, Kunsheng, Xiaofeng Yang, Miao Zhang, Ziwei Li, and Fanping Kong. 2019. "Objective Estimation of Tropical Cyclone Intensity from Active and Passive Microwave Remote Sensing Observations in the Northwestern Pacific Ocean" Remote Sensing 11, no. 6: 627. https://doi.org/10.3390/rs11060627
APA StyleXiang, K., Yang, X., Zhang, M., Li, Z., & Kong, F. (2019). Objective Estimation of Tropical Cyclone Intensity from Active and Passive Microwave Remote Sensing Observations in the Northwestern Pacific Ocean. Remote Sensing, 11(6), 627. https://doi.org/10.3390/rs11060627